基于測點優選和改進L曲線法的動載荷識別

李曉旺， 趙海濤， 陳吉安

(上海交通大學 航空航天學院， 上海 200240)

動態載荷識別[1]是結構動力學中的第2類反問題.目前，載荷識別方法主要有頻域法、時域法以及其他一些智能算法[2-4].對于每一種算法而言，其最終目的都是要建立起輸入載荷和輸出響應以及系統特性之間的數學模型.由于反求輸入載荷的過程需要對數學模型中的傳遞函數矩陣求逆，并且被測響應容易受到環境噪聲的干擾，往往會導致出現不適定問題.

為了盡量減小傳遞函數矩陣的病態性和響應噪聲對載荷識別精度的負面影響，國內外學者做了大量的研究工作.這些研究總體上可分為兩種思路：第1種思路為通過優化響應點的位置[5-6]獲得病態程度較低的傳遞函數矩陣，然后直接求廣義逆；第2種思路為避免對傳遞函數矩陣直接求逆，而是通過一定的技術手段對振動方程進行特殊處理，間接反演動態激勵，比較典型的方法有奇異值分解(SVD)法[7]和 Tikhonov 正則化方法[8].對于正則化方法來說，如何選擇正則化參數是關鍵，而L曲線法[9-10]是最為常用的計算正則化參數的方法.

然而，目前的研究鮮見將兩種思路結合起來.對此，本文提出在時域中分2步解決不適定問題.第1步對不同測點對應的傳遞函數矩陣進行分析，找出條件數最小的傳遞函數矩陣，從而獲得最佳測點.第2步采用Tikhonov正則化重構載荷.同時，針對正則化方法精度不高的缺點，在確定正則化參數的過程中對L曲線法進行改進，即引入B樣條函數[11]對L曲線進行插值，并通過計算B樣條曲線的各點曲率獲得更加準確的正則化參數.

1 基于Taylor多項式迭代的載荷識別方法

采用Taylor多項式迭代法[12]在時域內識別載荷時間歷程.對于一個多輸入多輸出的振動系統，其振動微分方程可表示為

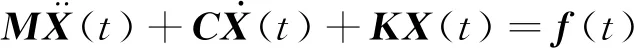
(1)

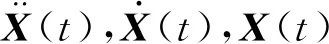
為了將振動方程解耦，總時間歷程被離散成n個時刻.對于任意相鄰的第i時刻t和第i+1時刻t+Δt，t+Δt時刻的振動響應被近似地表示為t時刻響應的Taylor多項式展開形式，即

(2)

(3)

(4)

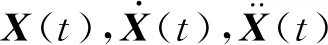
(5)

式中：A1,A2,Ad,Av,Aa,B1,B2,Bd,Bv,Ba,D1,D2,Dd,Dv,Da均為m×m階定常矩陣；下標a，d，v分別為加速度、位移和速度；F為從t1～tn+1時刻的全部激勵組合.

設結構自由度數為m，則對式(5)作遞歸可得到總線性離散方程為

(6)

式中：Yl為從t1～tn時刻的全部響應組合；Hl為總體傳遞函數矩陣.

2 載荷時間歷程重構

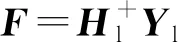
2.1 響應測點的優選方法

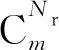
(7)

通過遍歷全部組合情況可以找到條件數最小的傳遞函數矩陣H，此時的測點組合Y即為最佳選擇，從而實現了響應測點的優化配置.

2.2 改進的L曲線法

在獲得最佳測點的響應值并確定了條件數最小的傳遞函數矩陣之后，采用Tikhonov正則化技術重構式(6)中的輸入載荷.設系統誤差e為

e=Y-HF

(8)

引入罰函數J的概念

J=(eTe)+λ(FTF)

(9)

當J對F的1階導數為0，誤差e達到最小值.此時激勵F可以表示為

F=(HTH+λI)-1HTY

(10)

式中：I為單位矩陣；λ為正則化參數.

正則化技術的核心在于如何選擇合適的正則化參數λ，L曲線法是常用的一種計算λ的方法.該方法的思路是選取一系列不同的λ值，分別計算每一個λ所對應的lg‖Y-HF‖和lg‖F‖值.然后以lg‖Y-HF‖為橫坐標，lg‖F‖為縱坐標作圖，其曲線形狀類似于字母“L”.在L曲線的拐點位置可找出曲率最大的一個點，該點對應的λ值即為最合適的正則化參數.

然而，傳統的L曲線法存在一定的缺陷.首先，該方法的第1步對λ值的選取具有一定的盲目性，很可能會遺漏最準確的λ值.其次，由于受到矩陣H奇異性的影響，對lg‖Y-HF‖和lg‖F‖求1階和2階導數很容易偏離真實值，從而直接造成L曲線的曲率計算結果不可靠.

為彌補上述不足，本文建立了基于B樣條插值的改進L曲線算法.首先依據常規方法獲得L曲線，然后截取L曲線的拐點部分(L-Co)進行插值操作，最后計算B樣條各點曲率從而獲得最佳正則化參數.

2.2.1L-Co的B樣條插值 設L-Co共有Nc個坐標，第j個坐標為(xj，yj)，其對應的正則化參數為λj，則共可以組成Nc個B樣條插值函數的控制頂點，任意一個控制頂點Pi可表示為

(11)

(i=0,1,…,Nc-1)

對L-Co進行k次B樣條插值后，曲線可寫為

(12)

0≤u≤1

式中：Ni,k(u)為定義在節點矢量U=[u0u1…uNc+k]上的k次B樣條基函數，Ni,k(u)的計算公式為

(13)

(14)

經過B樣條插值操作后，L-Co涵蓋的λ值遠遠超過預先選取的控制點的數量，避免了遺漏最佳正則化參數的可能.與選取同樣數量λ值計算L曲線坐標的傳統方法相比，B樣條插值操作的計算量要小的多.

2.2.2L-Co的各點曲率求解 經過插值操作后，計算L-Co各點的曲率問題可以轉化為計算B樣條函數的曲率問題.對k次B樣條曲線求1階導數的公式為

(15)

令

則式(15)可以改寫為

(16)

將式(16)和(12)比較可知，k次B樣條曲線的1階導數恰好是一條新的k-1次B樣條曲線.因此，求S(u)的2階導數只需根據式(15)計算S′(u)的1階導數即可求出S″(u)的值.插值后的L-Co是一條二維平面曲線，所以S′(u)和S″(u)分別對應坐標(x′，y′)和(x″，y″)，則L-Co各點的曲率Cu的計算公式為

(17)

曲率最小值所對應的λ值即為最優正則化參數，代入式(10)可以重構輸入載荷.

3 數值算例研究

為驗證所提方法的可行性和有效性，建立了3個不同的數值算例.3個算例所施加載荷的數量和復雜程度逐漸增加，擾動噪聲的水平也依次升高.采用本文算法分別對3個算例的輸入載荷進行重構，并與最差測點識別結果以及奇異值分解法識別結果進行對比.

3.1 正弦載荷識別算例

算例(T)1建立了一個懸臂梁模型，懸臂梁各項參數分別為彈性模量E=70 GPa，泊松比μ=0.35，密度ρ=2 700×103kg/m3，長寬高尺寸為600 mm×60 mm×30 mm.受正弦激勵的懸臂梁模型如圖1所示，對懸臂梁模型施加2個正弦時變載荷，2個動態激勵可表示為

(18)

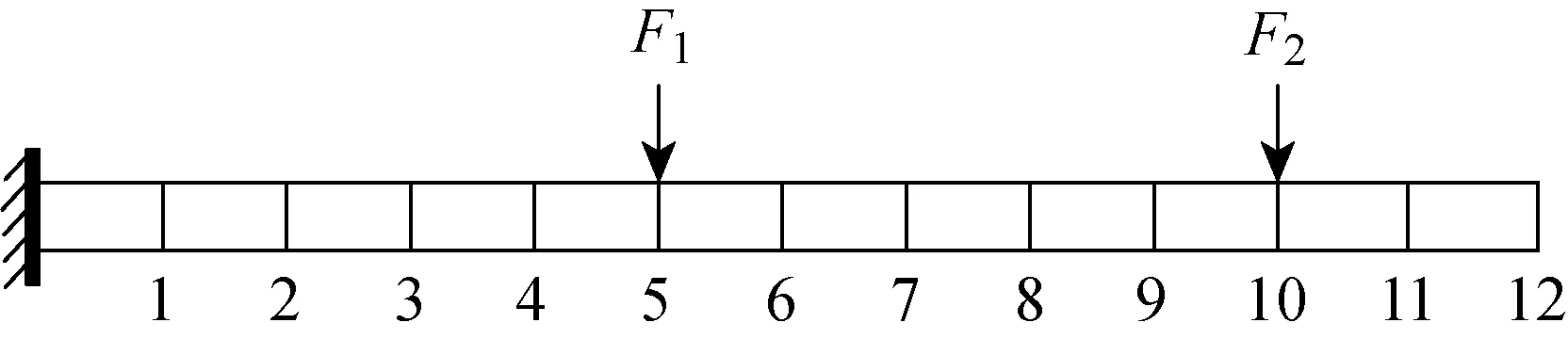
圖1 受正弦激勵的懸臂梁模型

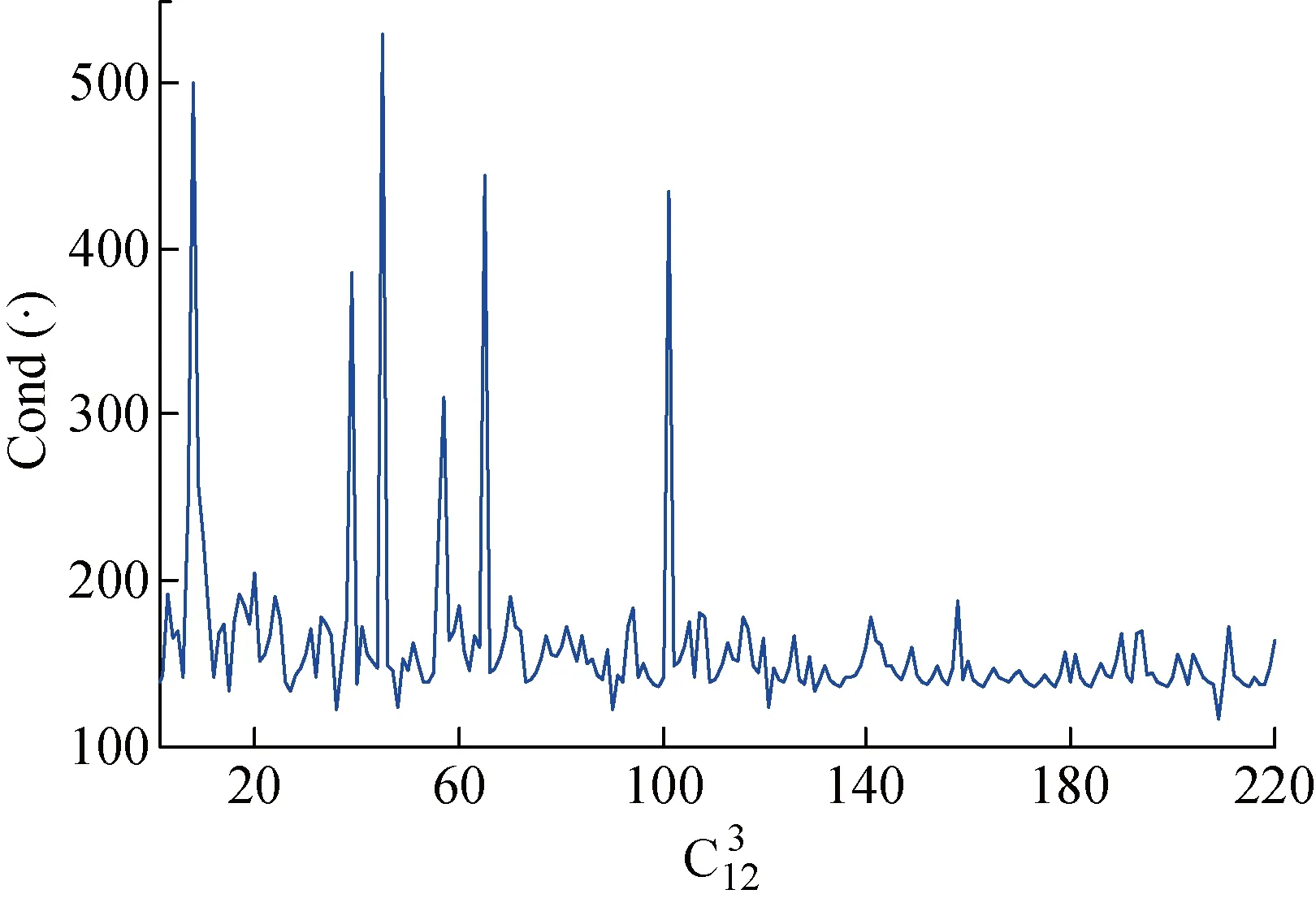
圖2 T1中不同測點組合對應的條件數

根據圖2可知，第209種組合情況可獲得最小條件數為97，對應最佳測點為7、10、12；第45種組合情況可獲得最大條件數為441，對應最差測點為1、7、12.

在分別獲得最佳測點和最差測點的響應值前提下，對被測響應混入5%的Gaussian白噪聲.采用改進的L曲線法計算最佳測點下的最佳正則化參數λ.T1中的整體L曲線如圖3所示，對L-Co進行B樣條插值的結果如圖4所示，所有λ對應的L-Co曲率如圖5所示，其中Cu為曲率.

由圖5可知，當λ=9.87×10-6時，L-Co的曲率達到最大值.將該λ值代入式(10)，即可反求輸入載荷的時間歷程.本文方法和兩種對照方法的識別結果如圖6所示，其識別誤差如表1所示.

由圖6可知，本文算法對正弦載荷的識別結果與真實值吻合得較好.由表1可知，本文算法的識別誤差低于另外兩種算法.同時，SVD法的識別誤差也保持在較低水平，低于選用最差測點的識別誤差.這說明對于載荷數量較少且形式簡單、噪聲影響水平較低的載荷識別問題來說，SVD法也可以適用，測點的選取對識別精度的影響要大于不同重構算法的影響.

圖3 T1的L曲線圖

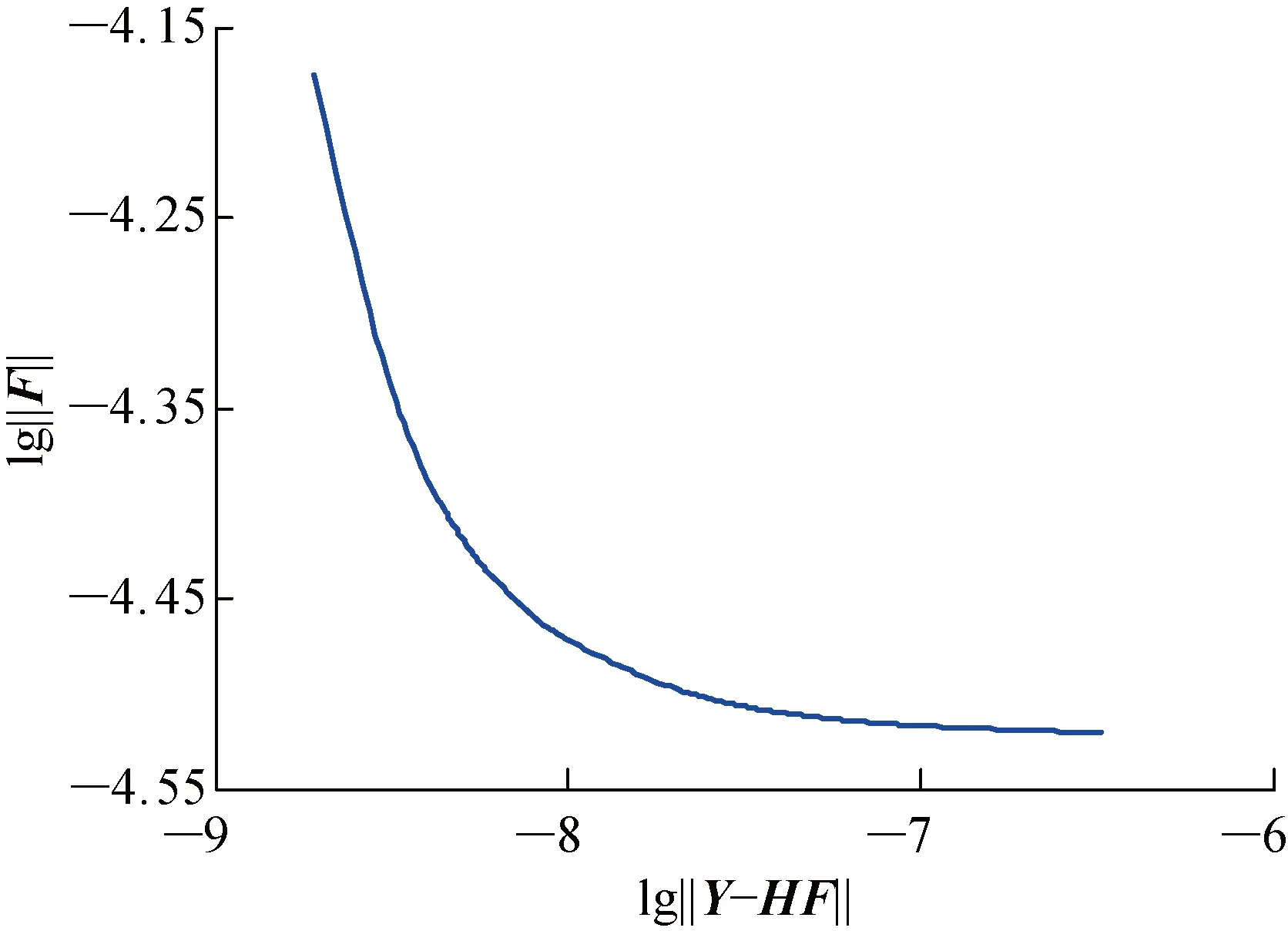
圖4 T1中L-Co的B樣條插值結果

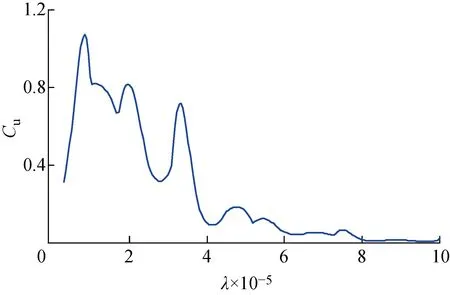
圖5 T1中L-Co各點曲率計算結果

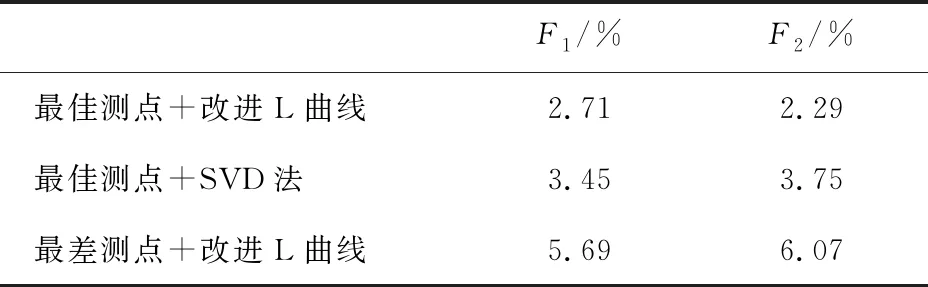
表1 T1載荷識別誤差

圖6 T1載荷時間歷程重構結果

3.2 正弦疊加載荷識別算例

T2選用和T1相同的懸臂梁模型，該結構受到3個正弦疊加載荷的激勵，受力情況如圖7所示.

3個動態激勵的表達式為

(19)

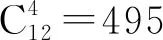
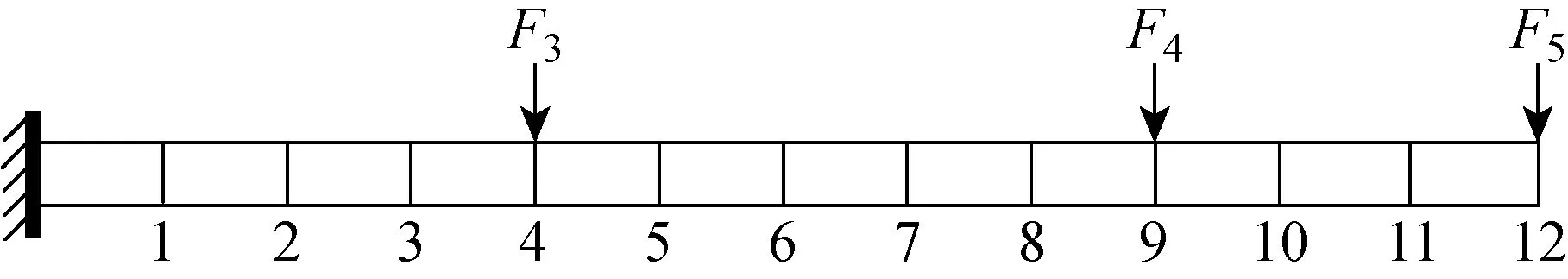
圖7 受正弦疊加激勵的懸臂梁模型

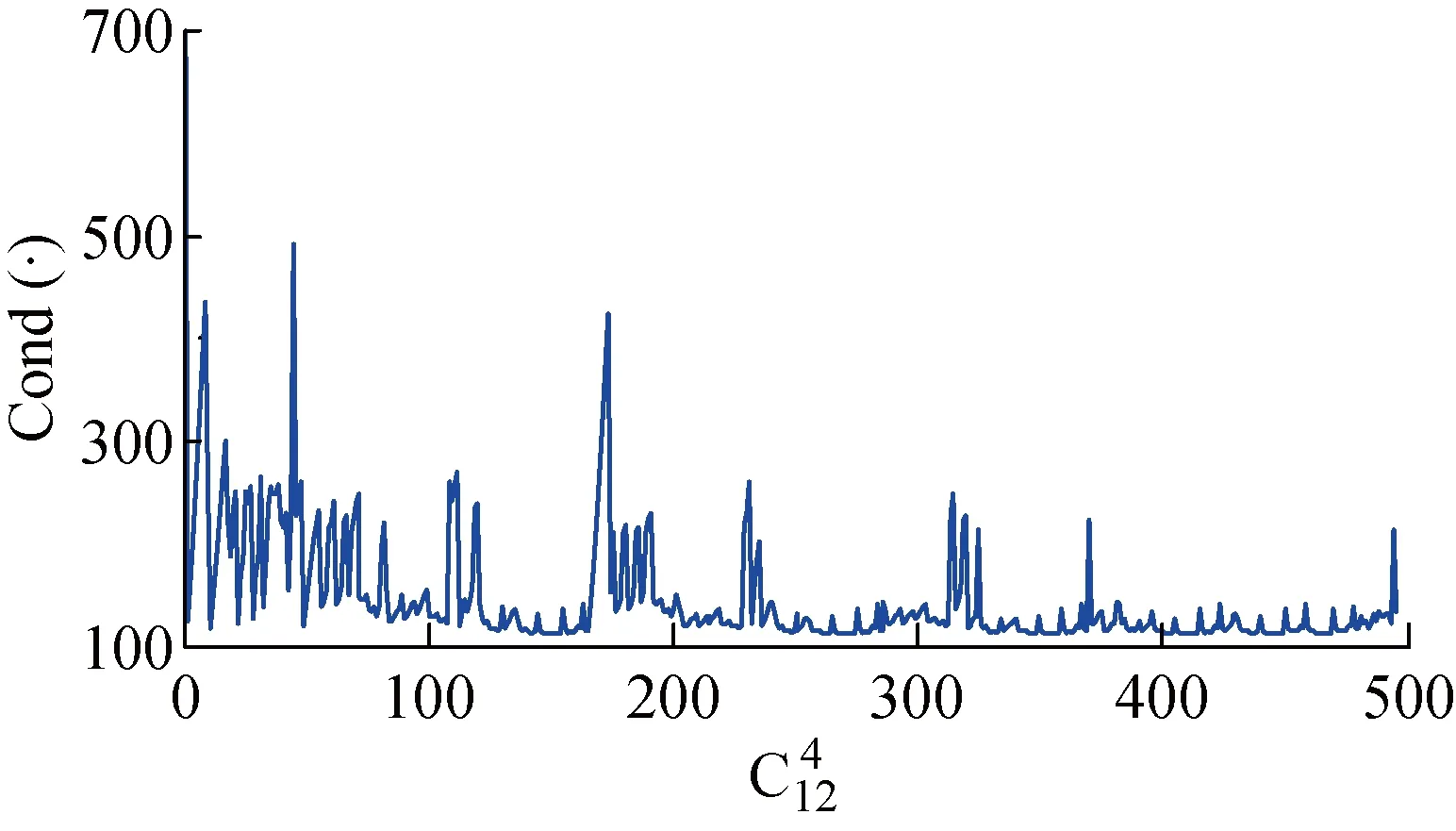
圖8 T2中不同測點組合對應的條件數

依據圖8所示的計算結果，當組合數為271時，得到最小條件數為112，對應的最佳測點為2、7、9、11；當組合數為1時，得到最大條件數為811，對應的最差測點為1、2、3、4.

接下來通過仿真獲得最佳測點和最差測點的響應值，對響應混入10%的Gaussian白噪聲.采用改進的L曲線法計算最佳正則化參數λ.圖9～11分別為T2的L曲線圖、B樣條插值后的L-Co圖，以及L-Co的曲率圖.

根據圖11中的曲率計算結果，當λ=2.06×10-5時，L-Co的曲率獲得最大值.將該λ值代入式(10)重構3個正弦疊加激勵的時間歷程.動載荷的識別結果如圖12所示，其識別誤差e如表2所示.

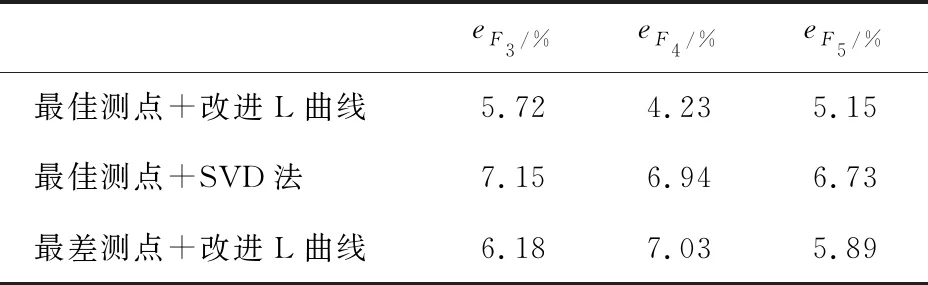
表2 T2載荷識別誤差

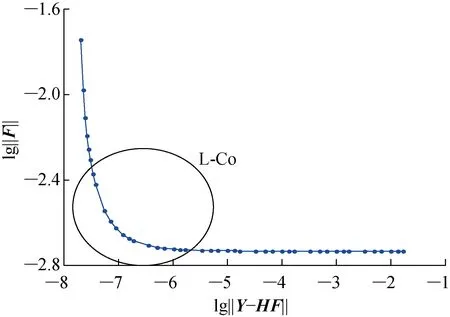
圖9 T2的L曲線圖

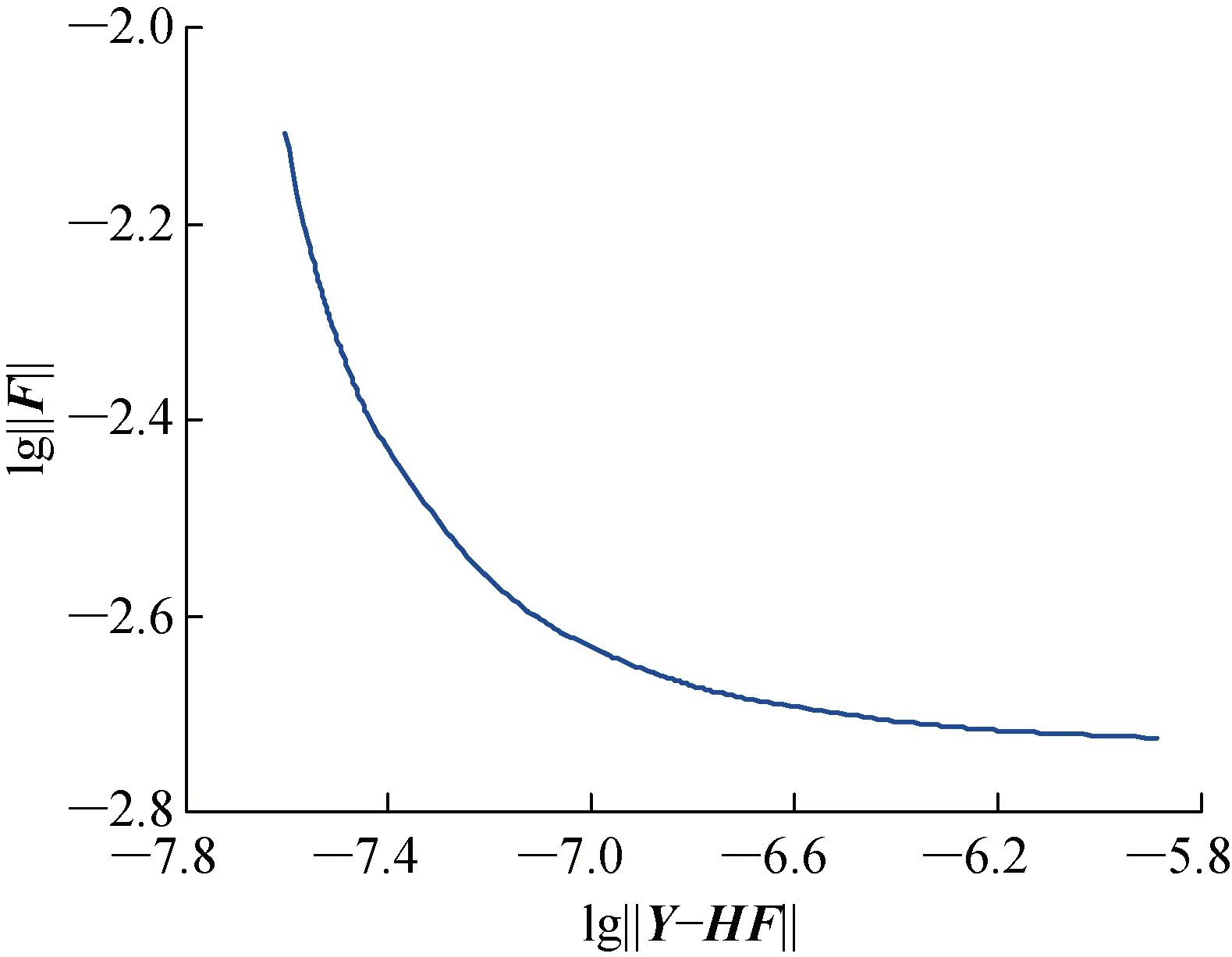
圖10 T2中L-Co的B樣條插值結果

圖11 T2中L-Co各點曲率的計算結果

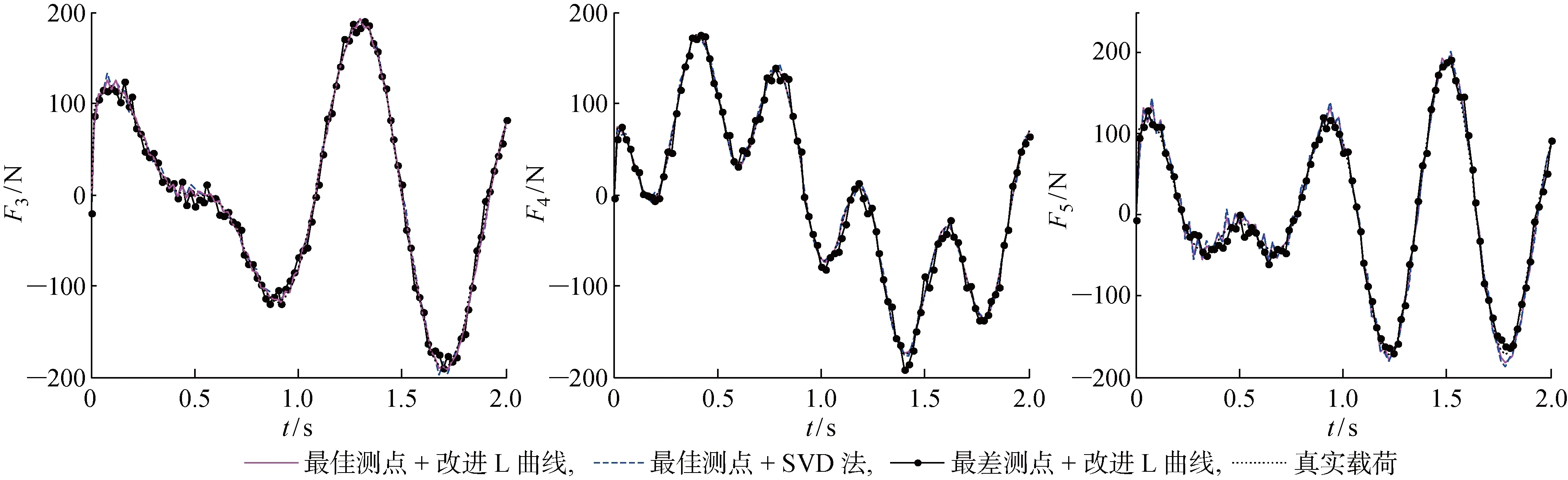
圖12 T2載荷時間歷程重構結果

由圖12可知，本文算法可以較為準確地反演出正弦疊加激勵的時間歷程，其識別結果相比于另外兩種算法更靠近真實載荷.從表2可以看出，由于T2的載荷復雜度、載荷數量以及噪聲水平均高于T1，導致算法的識別誤差比T1有所提高.而從數據值來看，3個載荷的識別誤差均在6%以下，仍屬于較低水平且低于兩種對照算法的誤差，體現了所提算法的優越性.

3.3 Gaussian白噪聲載荷識別算例

T3建立了一個桁架模型，其各項參數為E=200 GPa，μ=0.3，ρ=7 800×103kg/m3，截面積為20 cm2，所有水平桁架和豎直桁架的長度均為1 m.對桁架模型施加4個Gaussian白噪聲載荷，載荷幅值分別為80 N、70 N、60 N、50 N，如圖13所示.

由圖14可知，當測點組合數為595時，條件數取到最小條件數為194，對應的最佳測點為3、4、9、11、12；當組合數為109時，條件數取到最大條件數為 1 215，其對應的最差測點為1、2、7、10、12.

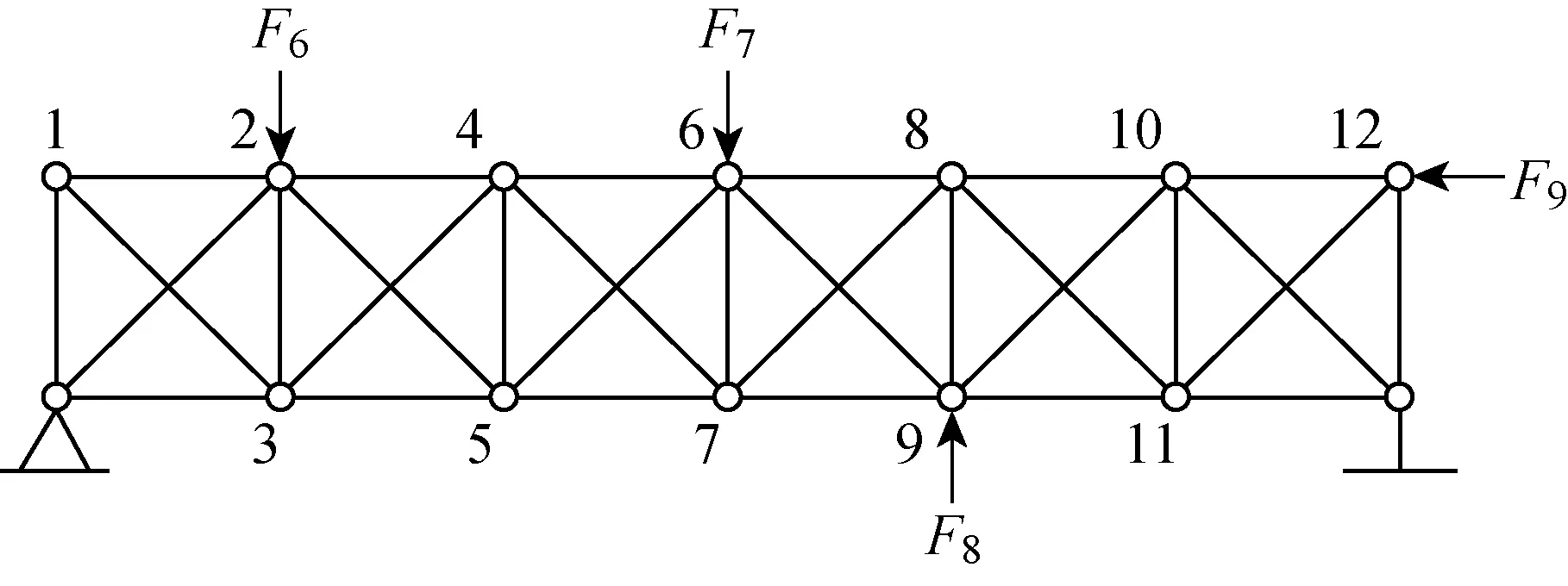
圖13 受Gaussian白噪聲激勵的桁架模型

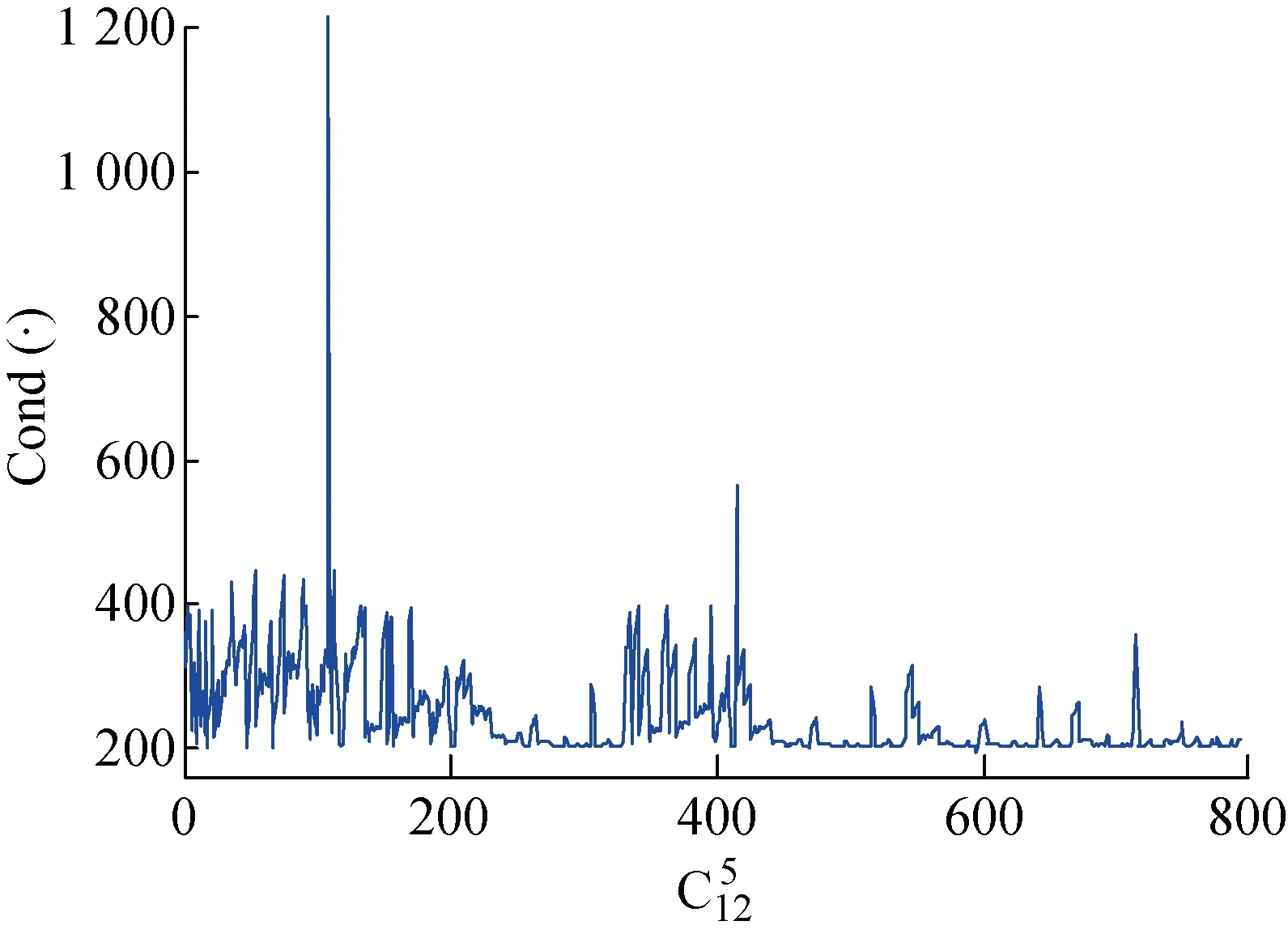
圖14 T3中不同測點組合對應的條件數

對被測響應混入15%的Gaussian白噪聲，然后采用改進的L曲線法求解正則化參數λ的最佳值.圖15～17分別為T3的L曲線圖、B樣條插值后的L-Co圖，以及L-Co的曲率圖.

由圖17可知，當L-Co的曲率達到最大值時，對應的最佳λ值為4.91×10-5.根據式(10)重構輸入激勵，T3的載荷重構結果如圖18所示，其識別誤差如表3所示.

與前兩個算例相比，T3的Gaussian白噪聲激勵是時變載荷中復雜程度最高的一種.從圖18中的被識別激勵時間歷程曲線可以看出， 本文算法重構的載荷與真實值的吻合程度顯著高于其他兩種對照算法，說明該算法具有優越的穩健性和抗噪性.由表3可知，本文算法的識別誤差雖然比T1和T2稍高，但仍處于較低水平且明顯低于對照算法.由于載荷數量較多，導致傳遞函數矩陣維數較大，即使選取最佳測點也有較強的病態性，從而引起SVD法的識別誤差迅速增大，此時不同識別算法對精度的影響超過了測點的選取對精度的影響.

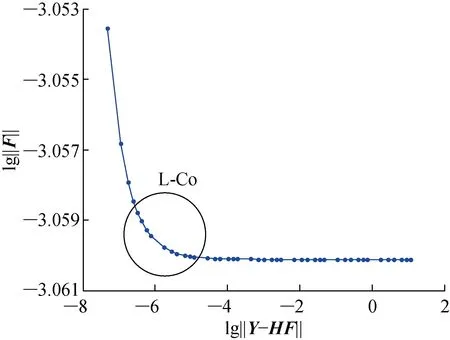
圖15 T3的L曲線圖

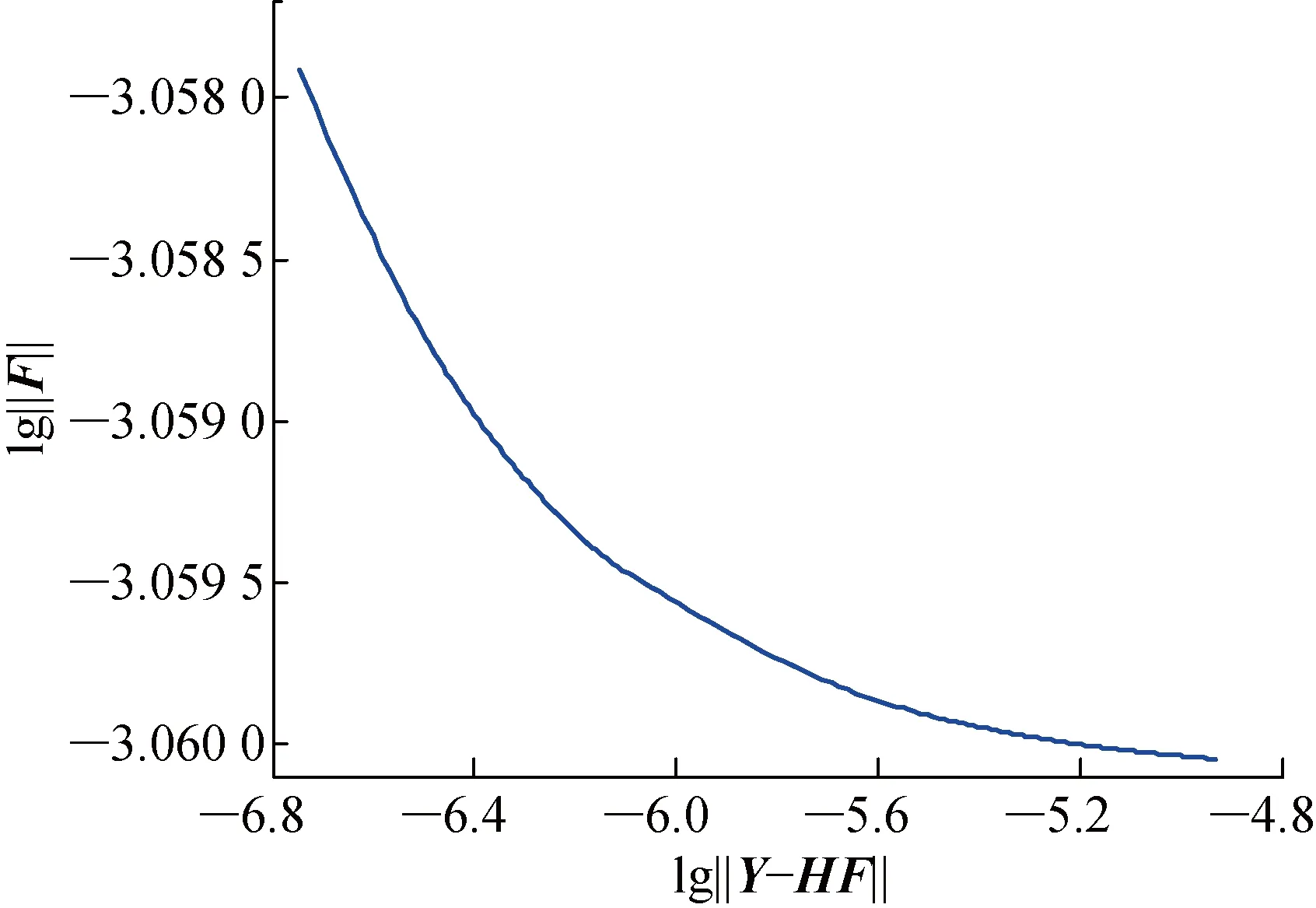
圖16 T3中L-Co的B樣條插值結果

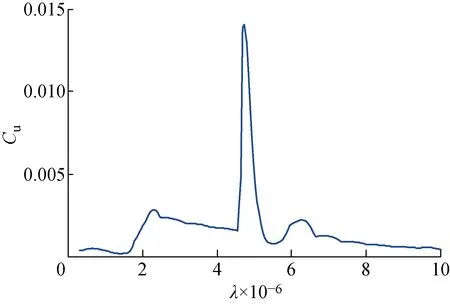
圖17 T3中L-Co各點曲率計算結果

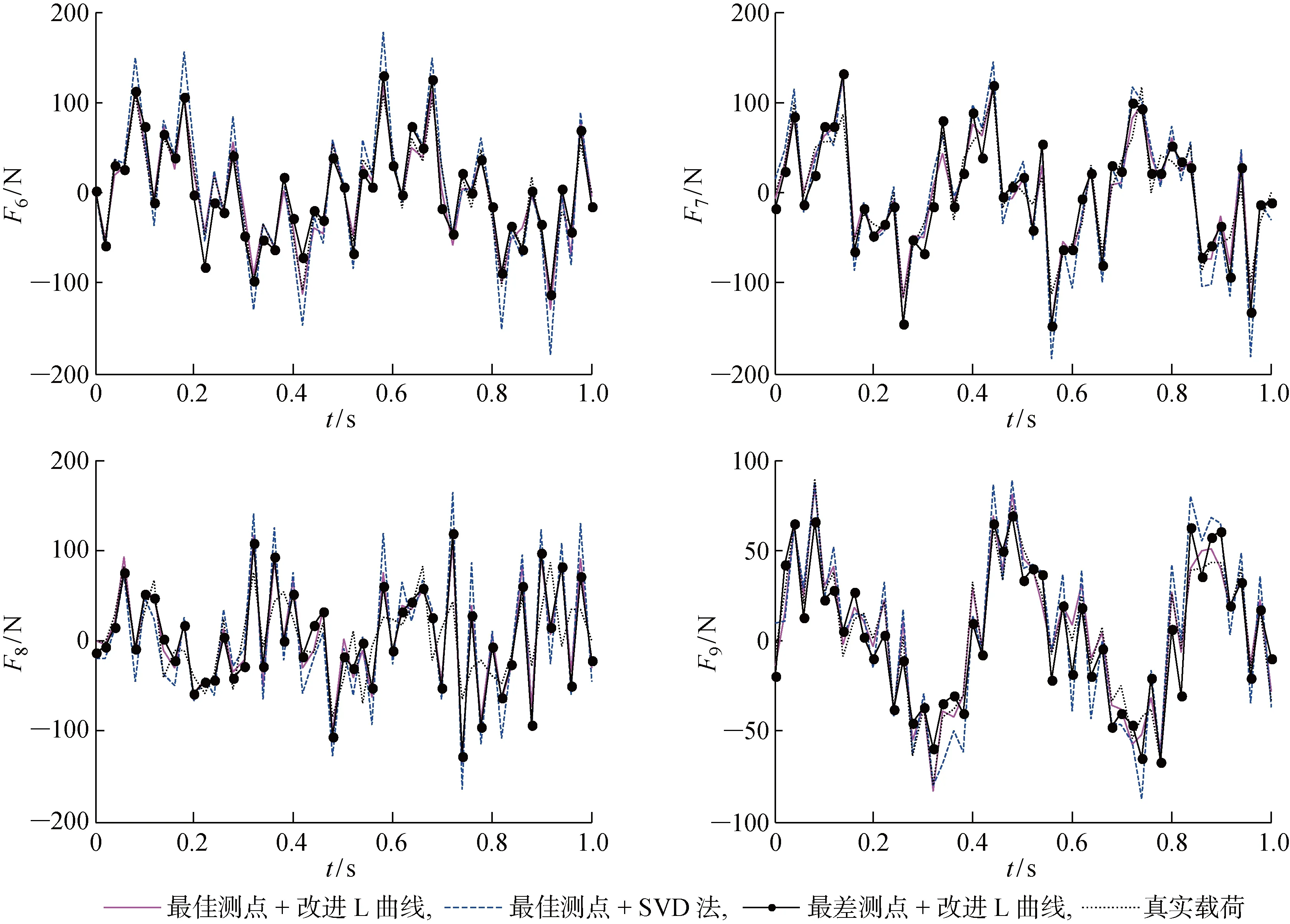
圖18 T3載荷時間歷程重構結果

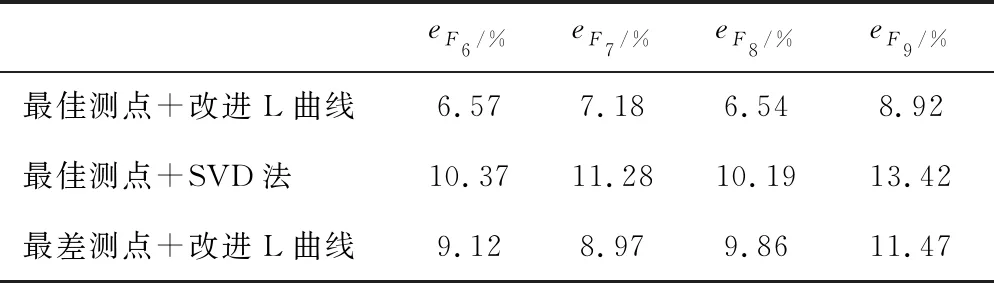
表3 T3載荷識別誤差

4 結語

針對載荷識別中的不適定問題，在時域內建立了測點優選和改進的L曲線法相結合的算法.首先通過遍歷所有測點組合找出條件數最小的傳遞函數矩陣，進而獲得對應的最佳測點.然后在使用正則化方法反求輸入載荷的過程中引入二次B樣條函數對L曲線進行插值，從而獲得了更加精確的正則化參數，并將該算法的載荷重構結果分別與最差測點識別結果以及SVD法識別結果作對比.數值算例結果表明，該方法可以有效減弱傳遞函數矩陣的病態性，并具有較強的穩健性和抗噪性，從而提高了載荷識別的精度.