Scratch算法練習

Intoweb

1. 為什么要做算法練習

對于計算機來說，針對一個問題選擇合適的解決方案的方法就是算法。算法可以是一系列的數學計算，也可以是一系列的操作步驟。總之，它存在的意義就是為了有針對性地解決問題。每個問題都有它獨特的一面，正所謂算法沒有最好的，只有最合適的。

軟件開發領域日新月異，編程語言會推陳出新，掌握的技術可能會淘汰，但算法卻是軟件不變的核心內容。因此，學好算法能夠有效提高編程能力，以后也能更好地學習新語言。

2. 什么是眾數

找眾數（Mode）是計算機程序設計入門的經典算法練習之一。在一組數據中出現次數最多的數值，叫眾數（Mode），多用于統計目標沒有明顯次序（如非數值性資料）無法良好定義算術平均數和中位數的情況。

例如：1，2，6，6，4，6的眾數是6。

有時眾數在一組數中有好幾個，如果有兩個或兩個以上數值出現次數都是最多的，那么這幾個數值都是這組數據的眾數。

例如：1，2，2，3，3，4的眾數是2和3。

如果所有數值出現的次數都一樣，那么這組數據沒有眾數。

例如：1，1，2，2，3，3列表共6項3種數值，出現次數最多是2次，列表數字出現次數的平均數也為2，所以沒有眾數。

現有一個長度為n的序列，請你編程求出它的眾數。當然眾數可能有多個，降低難度要求只需要輸出其中一個就可以了。

3. 算法分析

找眾數的算法有很多種比如“觀察法”、“金氏插入法”、“皮爾遜經驗法”等。由于題目只要求找到一個眾數即可，參考這些經典算法后有以下幾種思路供你參考。

1） 方法一：每次取出列表第一項，統計該項數值在列表中出現的次數，記錄下來，然后將該項刪除。這樣依次重復統計每項數值出現的次數，直到列表為空。

用專門變量記錄出現次數最多的那個數值，這個數值可能就是數列中的眾數。

除此之外，我們還需要排除所有數值出現次數相同的情況，如果這個數值出現的次數>列表數值出現次數的平均數，則代表眾數存在，否則就沒有眾數。數值出現次數的平均數=列表項目總數÷列表中數值的種類。

這種方法由于會刪除原列表1，所以是一種破壞型的方法。可以新增備份列表2解決這個問題。

2） 方法二：統計列表1中每一項數值出現的次數，一一對應存儲到列表2中，然后從列表2中找到最大的那個數，那么該項對應列表1的數就可能是眾數。

再看列表2中所有數是不是都一樣，只要有一個不一樣，那么列表1就存在眾數。

3） 方法三：先排序，然后找出那個重復最多的數就是眾數了。這種方法用到了排序，排序有很多種算法，本文不再詳述，你可以根據以前介紹過的排序方法想想看如何實現。

4. 方法一代碼分析

依次對比并記錄重復次數最多的數值，并刪除對比過的數值（如圖1）。

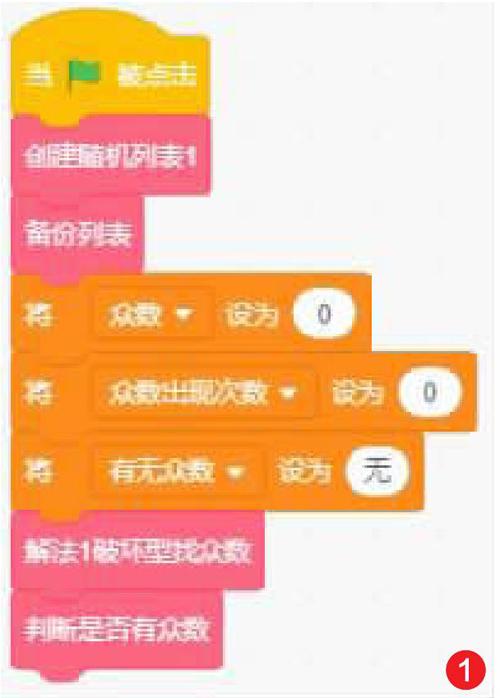
1） 創建變量：眾數、眾數出現次數、有無眾數用來記錄成果。列表長度、搜索項、搜索項次數、數字種類作為中間變量。index作為臨時變量。

2） 創建列表1，將隨機數加入這個列表。將列表1復制到備份列表2。解決找眾數過程中列表1會被刪除的問題（如圖2）。

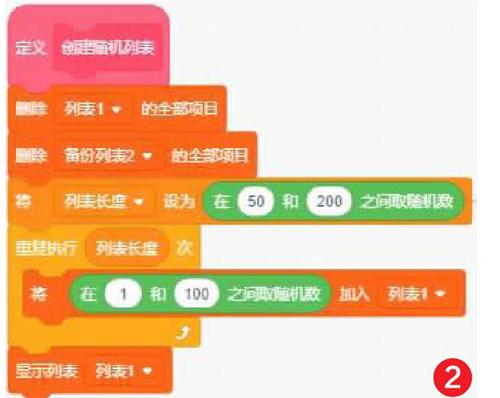
3） 初始化各個變量，有無眾數設為“無”，列表長度為列表1項目數。

4） 把列表1第1項設為“搜索項”，依次比對整個列表，記錄該搜索項出現的次數，并刪除所有與該搜索項相同的數值。這樣重復刪除直到列表1為空時就比對完成了。

5） 如果新的搜索項出現次數大于眾數出現次數，將眾數設為該搜索項，將眾數出現次數設為搜索項次數。當列表被清空時，眾數就是表中出現次數最多的數值了（如圖3）。

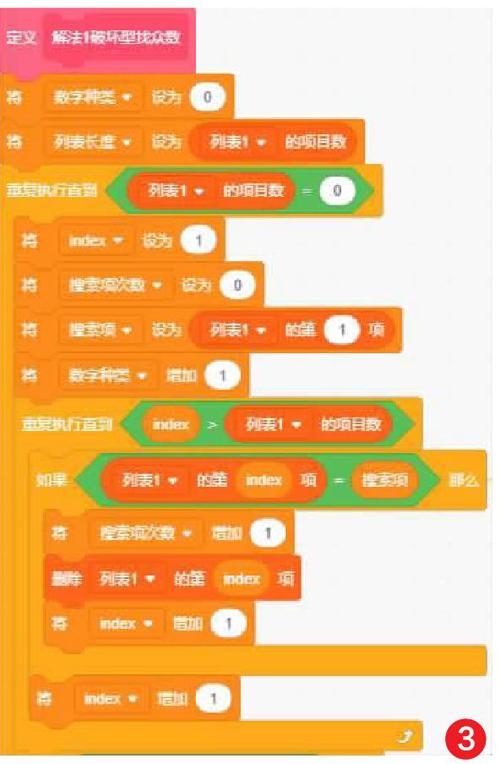
6） 判斷有無眾數。如果眾數出現次數大于數字出現的平均數就可以判斷有眾數了。如果有眾數就用連接塊整合輸出最終結果即可（如圖4，5）。

5. 方法二代碼分析

統計列表中每一項數值出現的次數，從中找到最大數，它對應列表中的項就是眾數（如圖6）。

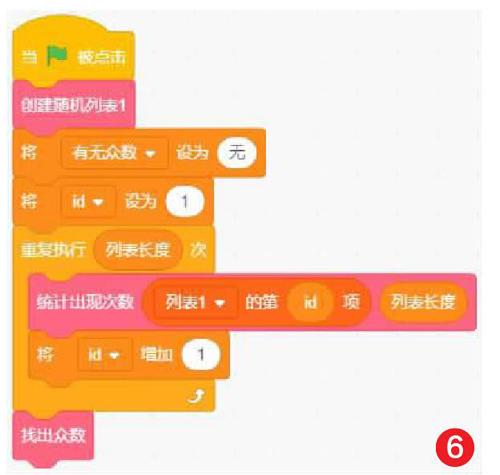
1） 定義變量：眾數是第幾項、眾數出現次數、有無眾數用來記錄眾數。搜索項、搜索項次數、列表長度、index用來統計列表每項出現的次數。

2） 生成隨機列表1，建立列表2用于存儲列表1每項在列表中重復出現的次數。

3） 統計列表某一項在列表中出現的次數。把列表搜索項依次比對整個表格，將重復出現次數記錄在搜索項次數中并存入列表2（如圖7）。

4） 完成統計后列表2中記錄了每項重復出現的次數，下面找出列表2中最大的項（如圖8）。

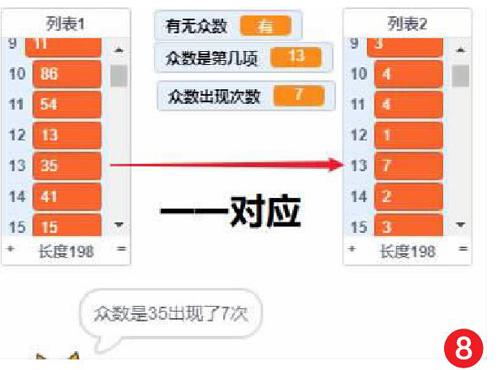
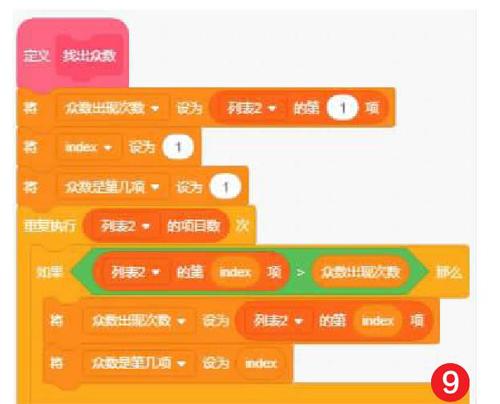
5） 找到列表2中最大的一項。從列表2第一項開始找到較大的項記錄在“眾數出現次數”中，重復“列表項目數”次就對比了全部項，這時“眾數出現次數”就是列表中最大的項，這項的順序位置記錄在“眾數是第幾項”中對應到列表1中就找到這個列表的眾數了（如圖9）。

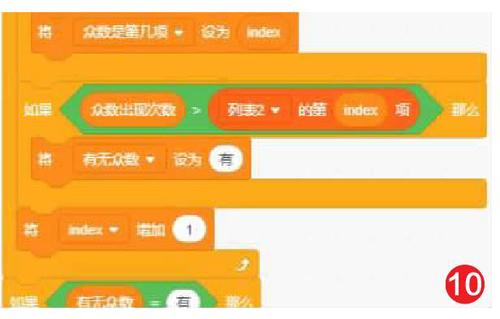
6） 在比對列表2中最大數的同時，我們還要同時判斷列表是否有眾數。只要列表2中的數值有一次出現不相等，就代表列表1有眾數（如圖10）。

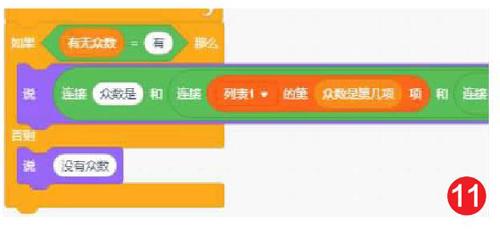
7） 輸出結果，完成循環。如果有眾數，用連接塊將結果說出來就可以了（如圖11）。

通過對兩種找眾數算法的簡析，我們練習了兩種找眾數的算法。你可以根據對這個問題的理解繼續改進算法或找到新的算法，還可以試試看能不能找到列表中所有的眾數。