無取向硅鋼片損耗特性模擬研究

李丹丹,朱聰聰,喬振陽,楊 娜,宋寅卯

(鄭州輕工業(yè)大學建筑環(huán)境工程學院，鄭州 450001)

近些年來，隨著中國電氣行業(yè)的飛速發(fā)展，電氣設備的節(jié)能降耗問題已成為各國學術界關注的熱點[1]。磁性材料的損耗是電氣設備的主要損耗之一，要提高電氣設備的運行效率，降低磁性材料的損耗，就需要精確地分析計算損耗，在電氣設備的設計過程中充分考慮磁性材料的損耗特性[2]。

對于損耗特性的研究，目前普遍使用的方法是Steinmetz提出的著名的磁滯損耗經驗公式[3]。該計算方法從磁滯損耗和磁感應強度以及磁化頻率之間的關系入手，認為磁性材料一個周期內的平均損耗，可以表示為頻率和磁通密度的函數(shù)。Steinmetz公式參數(shù)少，計算簡便，從而廣泛應用于正弦激勵下磁滯損耗的計算。中外學者對Steinmetz經驗公式進行了更加深入的研究。文獻[4]指出鐵心損耗與平均再磁化率直接相關，通過引入等效頻率的概念，提出了一種新的非正弦激勵下鐵心損耗的計算方法。文獻[5]進一步完善了鐵心損耗取決于平均再磁化率的假設，為了考慮小磁滯回環(huán)對鐵心損耗的影響提出了廣義Steinmetz公式，以減小在文獻[4]中改進Steinmetz公式預測損耗的偏差。文獻[6]指出了頻率和磁通密度對Steinmetz經驗公式系數(shù)的影響，通過大量的實驗數(shù)據(jù)擬合變系數(shù)公式，改進了傳統(tǒng)常系數(shù)經驗公式精度不高的缺點。文獻[7]提出了一種將磁滯損耗與磁化頻率、峰值磁通密度以及波形參數(shù)相聯(lián)系的改進的Steinmetz公式，以確定矩形和梯形電壓磁化下的磁滯損耗。

硅鋼片具有厚度均勻、磁導率高、矯頑力小以及磁滯伸縮效應低等特點，被廣泛應用于制作各類電機的鐵心[8]。根據(jù)內部晶粒方向的排列方式，硅鋼片可以分為取向性硅鋼和無取向性硅鋼。隨著硅鋼片的廣泛使用，中外學者逐漸開始關注其磁特性的研究。文獻[9]提出了一種直接描述硅鋼片磁場強度H與磁感應強度B之間數(shù)學關系的改進型矢量磁滯模型，并在考慮磁場強度波形諧波分量的同時，簡化磁阻系數(shù)及磁滯系數(shù)的表達式，提高了模型的模擬準確度。文獻[10]提出了利用磁能密度平均值與磁滯損耗密度分別計算磁阻系數(shù)和磁滯系數(shù)的方法，既保證了計算精度又縮短了計算時間。文獻[11]通過各種橢圓形磁化下?lián)p耗相對誤差的離散數(shù)據(jù)擬合得到損耗誤差項，來修正傳統(tǒng)旋轉橢圓損耗計算模型和正交分解損耗計算模型，有效地提高了旋轉損耗計算精度和工程實用性。

目前的研究無論是基于Steinmetz公式還是基于磁性材料磁特性模型，雖然提高了部分計算精度并擴大了其應用范圍，但是忽略了損耗與頻率之間的關系。因此，本文首先根據(jù)無取向硅鋼片的測量數(shù)據(jù)分析了損耗與頻率之間的關系，將經典的Steinmetz公式的計算參數(shù)表示為頻率的函數(shù)，進而提出了一種改進的損耗模型。并使用改進損耗模型對無取向硅鋼片在不同激磁頻率下?lián)p耗特性進行模擬研究，通過對模擬結果與實驗結果的對比分析可得，二者能很好地吻合，驗證了改進模型的有效性。

1 改進方法的提出

1.1 無取向硅鋼片的磁特性測量

選用無取向硅鋼片35ww270作為測量樣件，采用愛潑斯坦方圈測量法對樣件的磁特性進行測量，測量平臺使用長沙天恒測控技術有限公司研發(fā)的TD8510磁性能測試系統(tǒng)，如圖1所示。

圖1 愛潑斯坦方圈和TD8510磁性能測試系統(tǒng)Fig.1 Epstein square and TD8510 magnetictesting system

愛潑斯坦方圈由四個線圈組成，每個線圈中都有初級繞組和次級繞組。方圈安裝在一個絕緣的無磁性的底板上，且支撐線圈的繞組骨架由硬的絕緣材料制成，如酚醛樹脂紙板等。TD8510磁性能測試系統(tǒng)測量的頻率范圍高達1 kHz。勵磁源具有較強的輸出能力，最大磁化場達10 kA/m，有效勵磁功率達500 V·A/kg。

基于實驗測量得到的硅鋼片的磁特性數(shù)據(jù)，繪制出無取向硅鋼片在50 Hz下的多條磁滯回線，如圖2所示。可知，本文選用的無取向硅鋼片的磁滯回線不存在局部小磁滯回線，所以對該樣件不用考慮局部小磁滯回環(huán)的影響。在接下來的工作中將對無取向硅鋼片的損耗特性進行研究。

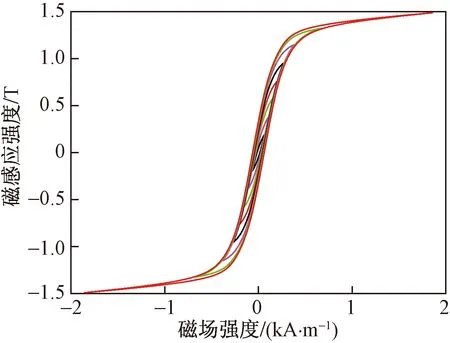
圖2 無取向硅鋼片磁滯回線Fig.2 Magnetic hysteresis loop of non-orientedsilicon steel sheet

1.2 頻率與損耗之間的關系

基于磁滯損耗形成機制，Steinmetz提出了著名的磁滯損耗Ph計算Steinmetz經驗公式[3]：

(1)

式(1)中：kh、α、β為正弦感應波形下實驗測得的經驗參數(shù)；f為磁化頻率；Bm為最大磁感應強度。

電工磁性材料在電工領域發(fā)揮著不可替代的作用，不同的磁材料具有不同的磁滯特性，為了更好地研究磁性材料，各國學者相繼提出了基于不同材料、不同激勵下的損耗計算公式，可歸納如下：

僅考慮矯頑磁場[12]：

(2)

考慮諧波磁場后分段變系數(shù)[13]：

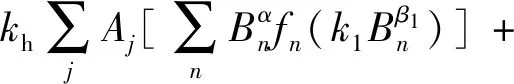
(3)

關于Bm變系數(shù)[14]：

(4)

單位時間總體積的平均損耗[15]：

(5)

單位時間單位質量的平均損耗[16]：

(6)

式(2)～式(6)中：Pt為總損耗；T為一個磁化周期；Hcr為矯頑磁場強度；kh為磁滯損耗系數(shù)；Aj為電機有限元模型中第j個單元的面積；fn為第n次諧波磁密的頻率；Bn為第n次諧波磁感應強度的幅值；k1、β1、k2及β2為磁感應強度項系數(shù)；α、β0、β1、β2、β3為計算參數(shù)；ABH為B-H環(huán)的面積；ρ為質量密度。

由式(1)～式(6)中各類損耗的計算方法可知，損耗與頻率存在正比關系，即損耗隨著頻率和磁感應強度的增加而線性增加。

根據(jù)實驗測量得到無取向硅鋼片的損耗數(shù)據(jù)，得出了不同頻率下?lián)p耗與磁感應強度的關系，如圖3 所示。

圖3 不同頻率下?lián)p耗與磁感應強度的關系Fig.3 The relationship between loss and magnetic density at different frequencies

由圖3可以看出，在最大磁感應強度一定時，損耗隨著頻率的增大而增大。隨著頻率的不斷增加，當最大磁感應強度數(shù)值較小時，損耗的增幅較小，當最大磁感應強度數(shù)值較大時，損耗的增幅較大。為了更直觀地看出頻率對損耗的影響，選取了最大磁感應強度為0.2、0.5、1.0、1.5 T時的損耗數(shù)據(jù)，繪制了不同磁感應強度下?lián)p耗與頻率的關系，如圖4所示。

由圖4可知，在最大磁感應強度一定的情況下，頻率在低頻階段時損耗增幅不明顯，而當磁感應強度增大時，損耗的增幅隨頻率的增加而增加。

進一步分析可知，在最大磁感應強度Bm一定的條件下，損耗隨著頻率f的增大而增大，但不是線性增長。根據(jù)對式(1)～式(6)中各類損耗計算公式分析可知，損耗與頻率呈正比關系，但通過對圖3和圖4進行分析可知，損耗與頻率并不是簡單的線性關系，假設出現(xiàn)這種現(xiàn)象的原因是損耗受到了頻率的非線性影響，并基于各國學者對損耗的研究成果，充分考慮頻率與損耗之間的關系，將Steinmetz公式計算參數(shù)設置成頻率的函數(shù)，進而提高了該公式的計算精度。

2 無取向硅鋼片的改進損耗模型

本文選取的無取向硅鋼片35ww270的密度為7.6×103kg/m3，電阻為49 μΩ·cm，其出廠數(shù)據(jù)如表1所示。

表1 無取向硅鋼片35www270的出廠數(shù)據(jù)Table 1 Factory data of non-oriented silicon steel sheet 35www270

為了研究無取向硅鋼片的損耗特性，需要對其建立損耗模型。首先，通過實驗測量得到了無取向硅鋼片35WW270在不同激磁頻率下的磁特性數(shù)據(jù)。其次，基于Steinmetz經驗算法得到在單位時間單位質量的無取向硅鋼片的系數(shù)，如表2所示。再次，根據(jù)這些系數(shù)將計算參數(shù)變?yōu)殛P于頻率的三次多項式，最后將擬合的多項式代入改進的Steinmetz經驗公式[式(7)]即可得到改進的Steinmetz損耗模型。

(7)

式(7)中：kh(f)是關于頻率多項式的損耗系數(shù)，α(f)、β(f)是關于頻率的三次多項式。

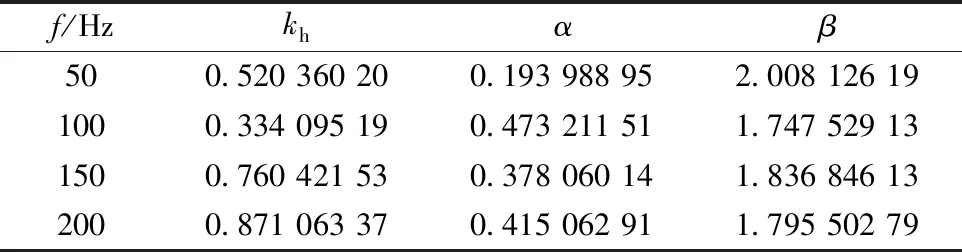
表2 單位時間單位質量無取向硅鋼片的系數(shù)Table 2 Coefficient of non-oriented silicon steel sheet per unit time unit mass

由表2中的系數(shù)kh、α、β為無取向硅鋼片35ww270磁材料在單位時間單位質量情況下的系數(shù)，根據(jù)這些系數(shù)可以擬合得到計算參數(shù)關于頻率f的三次多項式:

(8)

基于無取向硅鋼片擬合出的關于頻率f的三次多項式，在計算硅鋼片的損耗時，就可以將式(8)代入式(7)，即可分別得到不同頻率下的改進的Steinmetz損耗計算模型。

3 無取向硅鋼片的損耗特性的模擬研究

為了驗證改進的損耗模型的有效性，本文使用改進的損耗模型對不同激勵頻率下無取向硅鋼片的損耗特性進行了模擬，模擬的激磁頻率范圍與實驗數(shù)據(jù)一致，為50～200 Hz。隨后將改進模型的模擬結果與實驗結果進行了對比，如圖5所示。

結合圖5及誤差分析可知，在頻率為50 Hz的情況下，模擬結果與實驗結果基本一致，擬合效果較好，當頻率逐漸增加時，相對誤差逐漸增大，擬合效果有所下降。在圖5(d)中，激磁頻率為200 Hz時，改進損耗模型的擬合精度隨最大磁感應強度的增大而降低。因此，本文所使用改進的損耗計算模型在低頻低磁感應強度的情況下模擬精度較高，而在高頻高磁感應強度時模擬精度有待進一步提高。這是由于高頻高磁感應強度時材料磁化過程相對復雜，可能需要進一步對式(8)進行高階擬合或者考慮其他變量的影響來降低誤差，這將是下一步的工作重點。

4 結論

基于無取向硅鋼片磁特性測量數(shù)據(jù)，結合各國學者的研究成果，提出了一種改進的損耗計算模型。該模型考慮了損耗與頻率、磁感應強度之間的關系，將損耗模型的計算參數(shù)改為頻率的函數(shù)，在進行損耗計算時，充分地考慮頻率對損耗所產生的影響。最后，使用改進的損耗模型對無取向硅鋼片在不同頻率下的損耗特性進行了模擬，并將模擬結果與實驗結果進行對比分析，驗證了本文所提方法的有效性。