利用蜂群算法優(yōu)化的區(qū)域高程擬合精度分析

周 飛,張 炎,唐詩華,邢鵬威 ,張 躍

(1.廣西壯族自治區(qū)基礎(chǔ)地理信息中心，南寧 530023；2.桂林理工大學(xué)測繪地理信息學(xué)院，桂林 541006；3.廣西空間信息與測繪重點實驗室，桂林 541006)

隨著現(xiàn)代測量技術(shù)的快速發(fā)展，全球定位技術(shù)(global positioning system，GPS)在測繪工作中的應(yīng)用得以廣泛推廣，但GPS直接測定的是大地高，而實際工程中常用到的是正常高，兩者之前存在一個高程異常值，因此如何獲取高精度的高程異常值是GPS測量工作有待解決的問題[1]。目前常將粒子群算法、遺傳算法、人工神經(jīng)網(wǎng)絡(luò)等智能算法應(yīng)用于GPS高程擬合模型的構(gòu)建，近一步提高了待求高程異常值的精度。蒲倫等[2]提出了利用粒子群算法對傳統(tǒng)多面函數(shù)擬合方法進行優(yōu)化處理，近一步提高了多面函數(shù)中特征值的搜索效率，為擬合模型的構(gòu)建提供了合理的必要擬合參數(shù)。劉斌等[3]利用“移去-擬合-恢復(fù)”的思想，引出了基于EGM2008模型，并考慮地形因素影響的二次曲面擬合GPS高程的方法，模型的精度得到提高。劉建等[4]提出采用遺傳算法優(yōu)化徑向基(radial basis function,RBF)神經(jīng)網(wǎng)絡(luò)來達到全局搜索最佳徑向基函數(shù)中心值的目的，使得擬合模型能夠更好地預(yù)測高程。最小二乘支持向量機(least squares support vector machine,LSSVM)利用少量的數(shù)據(jù)樣本可以達到較好的高程擬合效果，關(guān)鍵之處在于最小二乘支持向量機中的正則化參數(shù)c和核參數(shù)σ，常規(guī)LSSVM擬合法中參數(shù)的優(yōu)化常選用交叉驗證法，但其存在計算量大且耗時長的缺陷，往往難以選定最佳參數(shù)值，擬合模型精度也難以達到期望值。尋求合適的方法提取最佳的參數(shù)值可以使擬合模型的精度得到進一步提升[5-6]。

相比其他智能算法，人工蜂群算法(artificial bee colony,ABC)具備參數(shù)少、計算簡潔、可全局搜索最優(yōu)值的特性[7]，現(xiàn)提出利用人工蜂群算法來優(yōu)化最小二乘支持向量機的GPS高程擬合方法，利用人工蜂群算法能夠快速廣泛有效的尋求最優(yōu)值的優(yōu)勢，為最小二乘支持向量機在規(guī)定的范圍內(nèi)找出最佳參數(shù)值，最終利用少量GPS水準重合點來構(gòu)建GPS高程擬合模型。

1 基本理論

1.1 人工蜂群算法

人工蜂群優(yōu)化算法是一種模仿蜜蜂尋找蜜源過程的生物智能優(yōu)化算法。一個蜂群中根據(jù)群內(nèi)工作的不同常常分為引領(lǐng)蜂、隨行蜂、偵查蜂三種類型，其中引領(lǐng)蜂的工作是將發(fā)現(xiàn)的食物源的信息傳遞和分享給其他在蜂穴中等待的伙伴，所傳的信息包括蜜源的方向、距離及存在的概率，隨行蜂在接收到引領(lǐng)蜂傳遞的消息后，嘗試尋找蜜源的具體位置，偵查蜂是尋找新的蜜源[8-9]。在蜜源搜尋工作中，引領(lǐng)蜂和隨行蜂各占蜂群的一半，其整個過程可以被理解為求取目標函數(shù)最優(yōu)值的過程。具體原理如下：

ABC首先要隨機產(chǎn)生類似于蜜源最佳位置的初始值xi(i=1,2,…,N),且N為蜂群蜜蜂的數(shù)量，待求解的空間大小與xi的范圍一致，蜜源的初始位置可以表示為

xi=md+rand(0,1) (md+Md)

(1)

式(1)中：md表示搜索范圍的最小邊界值；Md表示搜索范圍的最大邊界值；蜜源初始值隨機分布在(md,Md)的范圍內(nèi)。引領(lǐng)蜂在初始蜜源的周圍尋找新的蜜源Xj(j=1,2,…,N)，且新的蜜源位置不等于初始蜜源位置，可表示為

Xi=xi+φ(xi-xj)

(2)

式(2)中：φ是一個分布在[-1,1]之間的隨機數(shù)，利用貪婪算法來評價兩個蜜源的適應(yīng)度fit，決定進行更新或保留原先蜜源：

(3)

式(3)中：fi為目標函數(shù)值，進一步需要計算隨行蜂跟從引領(lǐng)蜂尋找蜜源的概率：

(4)

隨行蜂的加入進一步縮小搜索的范圍，并且每個隨行蜂根據(jù)在[0,1]內(nèi)產(chǎn)生的一個隨機數(shù)α來決定是否跟隨引領(lǐng)蜂，當pi>α?xí)r，隨行蜂才會按照式(2)產(chǎn)生一個新蜜源，通過貪婪算法來決定應(yīng)保留的蜜源，在經(jīng)過有限的迭代次數(shù)后若仍未找到更優(yōu)蜜源，則化為偵查蜂，根據(jù)式(1)尋求新的蜜源，若未放棄，則做出判斷并保留最佳值。

1.2 最小二乘支持向量機

最小二乘支持向量機是由Suykens在原有支持向量機的基礎(chǔ)上提出的，支持向量機具有結(jié)構(gòu)簡單、全局優(yōu)化、泛化能力較好等特性，而LSSVM在同時具備這些優(yōu)點之下還提高了收斂速度、化簡了計算過程[10-11]。其具體步驟如下。

針對給定的訓(xùn)練集：

A={(x1,y1),(x2,y2),…,(xl,yl)}∈(Rn×Y)l

(5)

式(5)中：xi∈Rn，yi∈Y=R,i=1,2，…,l,利用非線性映射將樣本輸入映射到高維特征空間，構(gòu)造出高維特征空間的線性回歸函數(shù)：

g(x,w)=wTφ(x)+b

(6)

式(6)中：w為權(quán)值向量；b為閾值。根據(jù)結(jié)構(gòu)風(fēng)險最小化原理，將其轉(zhuǎn)化為以下優(yōu)化問題：

s.t.yi=wTφ(xi)+b+ξi

(7)

式(7)中：c為正則化參數(shù)；ξ為誤差項；利用Lagrange函數(shù)和KKT(karush-kuhn-tucker)優(yōu)化條件可以求得LSSVM的函數(shù)模型：

Z(x)=ai[φ(xk)φ(xi)]+b

(8)

K(xk,xj)=[φ(xk)φ(xi)]

(9)

根據(jù)Hilbert-Schmidt原理，引入核函數(shù)[式(10)]，進而將高維空間的內(nèi)積計算轉(zhuǎn)換為原空間中的函數(shù)的計算，解決了高維特征空間的計算問題，即：

(10)

選用徑向基核函數(shù)作為LSSVM的核函數(shù)，以滿足GPS擬合建模需求，即：

(11)

從上面整個過程可以看出，利用最小二乘支持向量機構(gòu)建擬合模型只需要確定核函數(shù)參數(shù)σ和正則化參數(shù)c，相比原先，計算過程簡潔許多。

2 ABC優(yōu)化LSSVM

與其他智能算法相比，人工蜂群算法在搜尋目標函數(shù)最佳值的過程中不易受到自身參數(shù)的影響，且能夠進行全局性搜查，避免了陷入局部最優(yōu)值的缺陷[12]。該算法為最小二乘支持向量機選擇最佳參數(shù)值，建立較高精度GPS高程擬合模型。ABC-LSSVM組合法的具體步驟如下：

(1)對收集的高程擬合數(shù)據(jù)進行歸一化處理。

(2)ABC算法參數(shù)初始化：蜂群規(guī)模N，蜜源數(shù)量N/2，蜜源連續(xù)沒被更新次數(shù)限值limit，最大迭代次數(shù)max,待優(yōu)化參數(shù)個數(shù)D，參數(shù)的搜尋區(qū)間。

(3)確定初始值：在有效的范圍內(nèi)隨機設(shè)置初始值，并計算出每個初始值所對應(yīng)的LSSVM預(yù)測的均方根誤差(RMSE),將其作為目標函數(shù)。

(4)尋找新的蜜源：引領(lǐng)蜂利用式(2)對每個蜜源尋找產(chǎn)生新的蜜xi，并保證選擇的相鄰蜜源不是當前蜜源及未超出范圍，計算變異后的蜜源的目標函數(shù)值和適應(yīng)函數(shù)值，與當前蜜源進行比較，判斷當前蜜源是否需要進行更新，如果當前蜜源未更新的次數(shù)超過限制limit,則放棄該蜜源，尋找新的蜜源。

(5)再次開發(fā)新的蜜源：引領(lǐng)蜂將更新完的蜜源信息傳遞給隨行蜂，隨行蜂經(jīng)過相應(yīng)的概率比較來決定是否要對新的蜜源進行再次更新，若符合繼續(xù)開發(fā)的條件，隨行蜂進行再次開發(fā)的步驟同(4),并保留下最優(yōu)蜜源(解)。

(6)迭代次數(shù)達到最大值max:當隨行蜂的迭代次數(shù)達到最大值時，沒有再找到新的更優(yōu)蜜源，則隨行蜂轉(zhuǎn)化為偵查蜂，偵查蜂會通過式(1)產(chǎn)生新的蜜源。

(7)判斷更新的蜜源是否滿足條件，當新的蜜源(解)滿足最終要求，則保留最優(yōu)值，否則返回到(4)繼續(xù)尋找。

(8)LSSVM構(gòu)建GPS高程擬合模型：利用ABC優(yōu)化的最佳參數(shù)值，代入LSSVM中建立高程擬合模型，并通過檢測數(shù)據(jù)獲取擬合模型的內(nèi)外符合精度，進行比較分析。

經(jīng)過多次迭代尋求最佳值的過程，ABC-LSSVM可以進行全局性的搜尋到最佳參數(shù)，進一步加快收斂的速度，最終獲取最佳擬合模型。

3 實驗分析

3.1 采集研究數(shù)據(jù)

為驗證人工蜂群優(yōu)化最小二乘支持向量機擬合方法在構(gòu)建GPS高程擬合模型方面是否有效可行，同時與之前的方法構(gòu)建的模型進行精度對比分析，選擇了廣西東北方向部分地方作為研究區(qū)，覆蓋面積約在100 km2,地形條件較為復(fù)雜，山地略多，在研究區(qū)域內(nèi)采集了41個GPS點數(shù)據(jù)，點之間相隔為1.5～2.5 km，并與水準進行了聯(lián)測，點位精度均滿足研究要求，為蜂群算法優(yōu)化最小二乘支持向量機擬合法提供必要的基礎(chǔ)數(shù)據(jù)條件。在采集的41個GPS水準重合點中選擇出31個分布均勻的點用來構(gòu)建模型，剩余的10個GPS水準重合點用來檢驗人工蜂群優(yōu)化后的擬合模型精度，點位分布如圖1所示。分別利用優(yōu)化后的最小二乘支持向量機擬合法與其他兩種方法在同一批GPS水準重合點基礎(chǔ)上建立擬合模型，并對擬合結(jié)果進行對比分析。

圖1 測區(qū)點位分布Fig.1 Distribution of points in the survey area

3.2 擬合模型精度分析

在利用人工蜂群算法優(yōu)化最小二乘支持向量機擬合法構(gòu)建模型時，需要對初始值及迭代次數(shù)進行設(shè)置，將蜂群種群規(guī)模設(shè)置為20，蜜源連續(xù)沒被更新次數(shù)限值設(shè)置為100，最大迭代次數(shù)為80。由于LSSVM在進行擬合模型的構(gòu)建時需要優(yōu)化的參數(shù)只有正則化參數(shù)c和核參數(shù)σ，因此待解問題的維數(shù)D=2，取值范圍均為(0.01,50),最后將擬合的結(jié)果與BP神經(jīng)網(wǎng)絡(luò)擬合法、常規(guī)LSSVM擬合法的結(jié)果進行對比分析。為初步驗證擬合模型的穩(wěn)定及有效性，分別利用3種不同擬合方法進行了多次試驗，如表1所示為10次實驗中模型的內(nèi)符合精度。

表1 三種擬合方法的內(nèi)符合精度比較Table 1 Comparison of internal accuracy of three fitting methods

根據(jù)表1統(tǒng)計可知，在10次的實驗中，人工蜂群優(yōu)化后建立的模型內(nèi)符合精度均值為2.7 mm,常規(guī)LSSVM構(gòu)建模型均值為4.7 mm,BP神經(jīng)網(wǎng)絡(luò)擬合法為5.6 mm,無論是均值還是10次實驗中內(nèi)符合精度的波動范圍，ABC-LSSVM組合擬合法構(gòu)建的模型均優(yōu)于其他兩種方法，且穩(wěn)定性更為理想。

為了更加詳細的對比分析3種方法的擬合效果，利用三種方法建立的擬合模型，獲取了10個擬合檢測點的高程異常值，并對檢測點的擬合殘差進行對比分析(表2)。

從表2可以看出，ABC-LSSVM組合法的檢核點殘差平均值及殘差平方均值均要小于其他兩種方法，經(jīng)過對實驗數(shù)據(jù)分析可以看出該方法的擬合結(jié)果的變化范圍較小，擬合精度較高；而BP神經(jīng)網(wǎng)絡(luò)擬合法的變化范圍最大，擬合精度最為不穩(wěn)定，在用來建立GPS高程擬合模型時難以達到理想的精度；為了更近一步直觀地顯示ABC-LSSVM擬合法的有效可行性，繪制了10個檢核點的殘差變化對比圖(圖2)。

圖2 三種擬合方法的殘差對比Fig.2 Residual comparison of three fitting methods

圖2直觀形象地展示了人工蜂群優(yōu)化擬合法比常規(guī)最小二乘支持向量機擬合法更好。根據(jù)檢測點的殘差走勢圖可以看出，BP神經(jīng)網(wǎng)絡(luò)擬合法的殘差數(shù)值波動最大，常規(guī)LSSVM的波動略低于BP神經(jīng)網(wǎng)絡(luò)，但相比與蜂群優(yōu)化法，其后5個檢核點的殘差值均高于蜂群優(yōu)化法，整體的波動范圍遠也大于蜂群優(yōu)化法，從總體精度上講，人工蜂群優(yōu)化擬合法的模型精度最佳，能夠充分的表示出實際地形特征，構(gòu)建的擬合模型精度也有所提高。

為增強10個檢核點的精度評定結(jié)果的可信度，更加形象地展示模型的精度，分別利用3種方法進行多次試驗，統(tǒng)計了15次實驗中檢核點的外符合精度及均值，通過所有實驗的平均值與單次的測量值進行比較分析，獲取最為合理的GPS擬合模型的精度，最終的測試結(jié)果如表3所示。

表2 檢測點的擬合殘差對比Table 2 Comparison of fitting residuals of detection points

根據(jù)表3中的數(shù)據(jù)可看出，無論是每次實驗的外符合精度還是15次實驗后的精度均值，人工蜂群改進的擬合法均要優(yōu)于其他兩種方法，經(jīng)計算后蜂群改進的擬合法構(gòu)建的擬合模型平均精度為±19.8 mm,在選用相同的一組測試數(shù)據(jù)的基礎(chǔ)上，常規(guī)的LSSVM擬合法的擬合精度為±27.5 mm，蜂群優(yōu)化法的精度比其提高了28%，與BP神經(jīng)網(wǎng)絡(luò)擬合方法相比，人工蜂群優(yōu)化最小二乘支持向量機擬合法構(gòu)建模型的精度提高了36.1%，充分說明了人工蜂群優(yōu)化擬合法可以提高GPS擬合模型的精度。

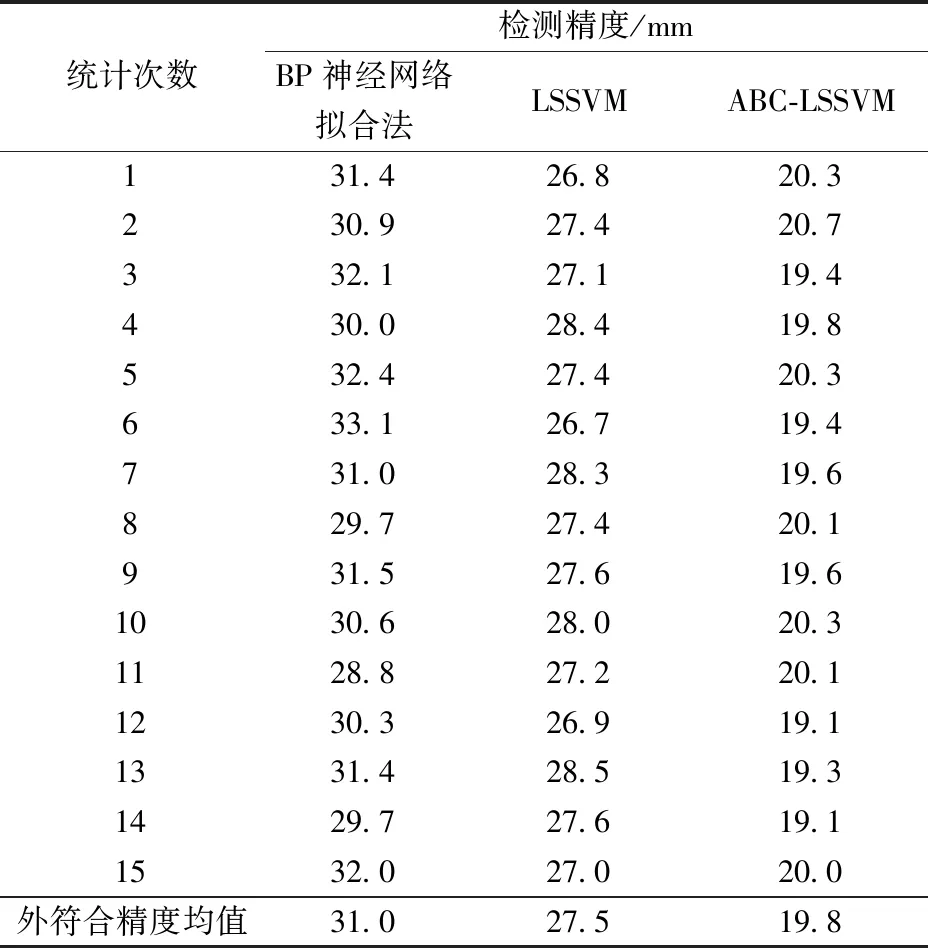
表3 不同方法的檢測精度比較Table 3 Comparison of detection accuracy of different methods

4 結(jié)論

為了解決最小二乘支持機擬合方法建立GPS高程擬合模型時參數(shù)選擇較為困難的問題，提出利用人工蜂群算法對最小二乘支持向量機擬合法進行參數(shù)優(yōu)化，并通過實驗與其他方法進行了對比分析，得出如下結(jié)論。

(1)在人工蜂群優(yōu)化算法中，設(shè)置隨機初始值及迭代次數(shù)最大值，選定參數(shù)固定范圍，通過不同的分工來增加生物的多樣性，確保最終的獲取結(jié)果為全局最優(yōu)，避免陷入局部最優(yōu)解的麻煩，尋優(yōu)過程中工作性質(zhì)的不斷轉(zhuǎn)換提高了收斂速度，短時間內(nèi)為最小二乘支持向量機構(gòu)建擬合模型提供了最佳的擬合參數(shù)。

(2)常規(guī)最小二乘支持向量機擬合法常通過交叉驗證法尋求擬合模型參數(shù)，而本次利用人工蜂群算法進行參數(shù)尋優(yōu)，多次實驗內(nèi)外符合精度統(tǒng)計及殘差走勢圖均表明人工蜂群算法優(yōu)化擬合法的收斂效果更佳，在有效的搜索范圍內(nèi)，更加有利于搜索最優(yōu)值的效率。

(3)根據(jù)實驗結(jié)果可知，相比其他兩種方法，蜂群優(yōu)化擬合法的建模精度較高。其擬合模型的總體精度為±19.8 mm,比常規(guī)最小二乘支持向量機擬合法提高了28%，比BP神經(jīng)網(wǎng)絡(luò)擬合法提高了36.1%，充分證明了人工蜂群優(yōu)化擬合法的有效可行性。

提出的蜂群優(yōu)化最小二乘支持向量機擬合法在建立模型中是否有效可行得到了充分的驗證，但是實驗區(qū)域范圍有限，針對較大范圍的擬合區(qū)域，該方法構(gòu)建擬合模型的穩(wěn)定性和有效性需要進一步驗證。