基于雙體結構的無人測繪艇航向控制

周 健,王晨旭,張安民

(天津大學海洋科學與技術學院，天津 300072)

隨著智能化時代的進展，無人化系統在各領域中的應用越來越廣泛，其在海洋測繪中體現為以無人艇為平臺搭載各類設備的綜合測量系統。為了實現水面無人艇的自主航行，通常必須解決三方面的內容，即航向穩(wěn)定、航線跟隨與自主路徑規(guī)劃[1]。因此航向控制是無人艇能夠準確執(zhí)行任務的基礎，也是關鍵所在。無人艇的航向控制算法多種多樣，當前大部分學者采用的方法主要包括神經網絡控制、自適應控制、模糊控制和魯棒控制[2]等：Naeem等[3]針對Springer號雙體無人艇，設計了基于線性高斯理論和遺傳算法的航向控制器；譚西都[4]設計了一種專門用于海上搜救的雙體無人艇，并通過智能自整定PD航向控制器實現其航向控制；Fang等[5]研究了一種基于模糊神經算法的航向自整定器，但其實現過程較為復雜；武穎等[6]利用反演滑模控制理論設計了針對欠驅動水面無人艇的航向控制器，并通過計算機仿真和實船試驗驗證了算法的有效性。李小毛等[7]提出了一種基于α-β濾波的無人艇航向角控制方案，這種方法不同于傳統的控制理論，實現了航向角全值域的濾波。現設計一種雙體無人測繪艇，介紹其設計理念并采用RBF(radial basis function)神經網絡結合PID(proportion integration differentiation)控制算法實現對其的航向控制。

1 雙體無人艇整體設計

為了滿足更加復雜惡劣海況下的測繪需求，設計一種基于雙體結構的無人測繪艇，如圖1所示。無人艇采用碳質橫骨架連接的雙體結構，能夠獲得更加穩(wěn)定的航行效果和抗風浪能力。艇身兩側浮體后各安裝一個由電動機驅動的螺旋槳，通過雙槳轉速配合可平穩(wěn)地實現原地旋回轉向。在試驗中，該艇可以滿足在河流、湖泊、海洋(1～3級海況)等環(huán)境中安全工作的要求。

圖1 雙體結構無人測繪艇Fig.1 Unmanned surveying and mapping catamaran

為充分滿足測量要求，無人艇應搭載雷達、單(多)波束測深儀、測距儀、AIS(automatic identification system)、IMU(inertial measurement unit)系統、攝像系統等儀器設備。因此在設計過程中，艇身選用輕型碳質材料搭配鋁合金底座，整體質量適中，同時無人艇開敞的上層空間有利于更多設備的搭載與固定。表1中給出了該無人艇的各項詳細參數。

表1 無人艇各項指標參數Table 1 Parameters of the unmanned surface vehicle

2 無人艇航向控制策略

2.1 典型PID控制

PID控制技術是當前在工程領域中最廣泛使用的反饋控制技術，由比例、積分和微分三部分單元組成[8-9]。比例、積分和微分這三個PID控制器的糾偏環(huán)節(jié)用于減小系統偏置，加快系統響應速度，PID自動控制器的原理如圖6所示。

圖2 PID自動控制原理圖Fig.2 Diagram of PID automatic control

從圖2可以看出，偏差e(t)是輸入值r(t)與輸出值y(t)的差值。在PID模塊中先對系統偏差e(t)進行比例、微分和積分運算，相加后得到PID控制器的輸出u(t)。連續(xù)時間中PID算法控制律表達式為

(1)

圖3、圖4中的仿真曲線表示僅用PID算法控制無人艇運動時航向與雙螺旋槳轉速差值隨時間的變化效果。設置輸入航向為100°，并通過手動調節(jié)PID模塊中的系數Kp=0.45、Ki=-0.000 3、Kd=0，使系統能夠達到比較理想的效果。可以看出，單一的PID控制基本能夠達到船舶航向控制的要求，但系統達到穩(wěn)定時的調節(jié)時間較長，而且Kp、Ki、Kd的值也無法通過自學習達到最佳水平。因此考慮設計一種能夠降低系統調節(jié)時間和超調量并能夠自動更新各系數的控制方法。

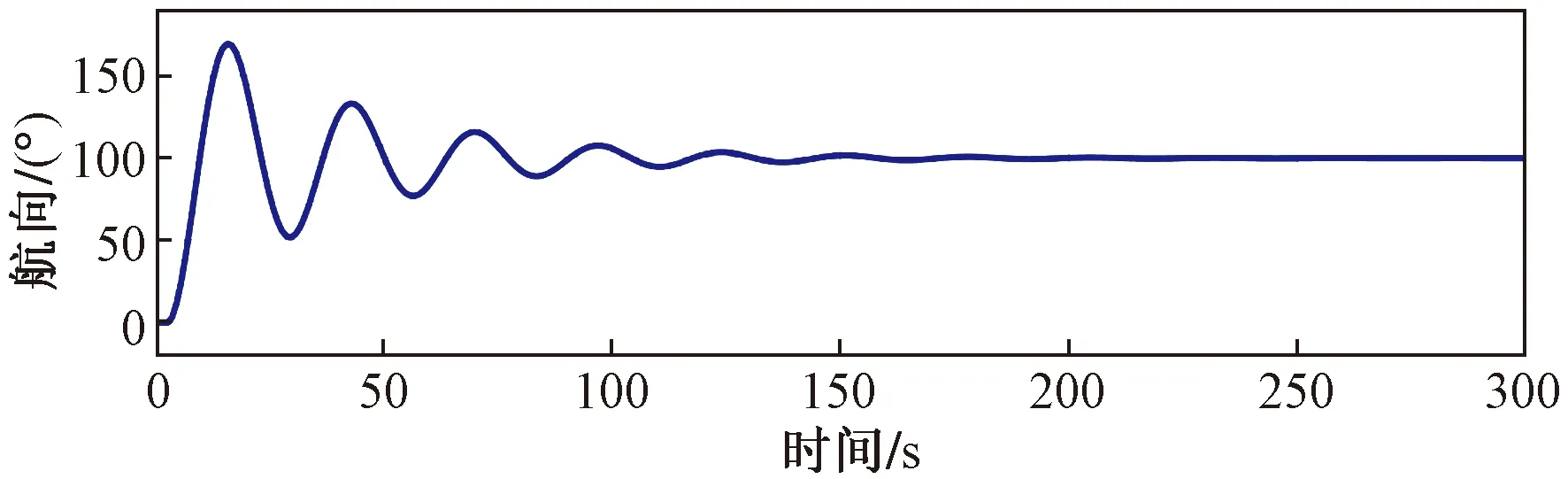
圖3 PID控制航向變化Fig.3 Course change of PID control

圖4 PID控制雙槳轉速差變化Fig.4 Speed difference between propellers of PID control

2.2 基于RBF神經網絡的PID控制

2.2.1 RBF算法原理

RBF神經網絡具有單隱層的三層前向反饋網絡結構。由于RBF神經網絡可以在局部以任意精度逼近非線性連續(xù)函數，因此廣泛應用于非線性控制、模式分類、圖像處理等研究領域。RBF神經網絡的另一個特殊性在于輸入層到隱含層的權重始終為1，在深度復雜網絡的訓練中可以減少求解次數。設RBF網絡徑向基向量，H=(h1,h2,…,hm)，hj為高斯基函數，其具體形式為[10]

(2)

式(2)中:輸入向量X=(x1,x2,…,xn)T;高斯基函數中心向量Cj=(cj1,cj2,…,cjn)T；bj是高斯函數中第j個隱層神經結點的形狀參數，也稱為基寬度。因此神經網絡輸出為

(3)

式(3)中:wi為神經網絡隱層到輸出層的權重系數。因此RBF神經網絡的性能指標函數為

(4)

式(4)中：y(k)是k時刻控制系統的輸出值；ym(k)是k時刻神經網絡的輸出值。根據梯度下降算法，輸出權重、中心向量以及基寬度參數的迭代算法為

(5)

式(5)中：η為學習速率；α為慣性系數。

2.2.2 RBF神經網絡PID控制器

基于RBF神經網絡的PID控制器中包含PID控制器和RBF神經網絡辨識器[11]。辨識器通過被控對象的輸入和輸出來訓練出被控系統的近似模型，最終使神經網絡的輸出與被控對象的輸出一致。在模型訓練的過程中，除神經網絡中各參數參與訓練外，PID控制系統的參數Kp、Ki、Kd也由神經網絡自適應調整至最佳水平。RBF神經網絡PID控制器結構如圖5所示。

圖5 RBF神經網絡控制器Fig.5 RBF neural network controller

控制系統的誤差為

e(k)=r(k)-y(k)

(6)

PID控制器的輸入為

(7)

PID的控制算法為

Δu(k)=Kpxc(1)+Kixc(2)+Kdxc(3)

(8)

根據梯度下降法，對模型訓練過程中的Kp、Ki、Kd進行迭代[12]：

(9)

式(10)為Kp、Ki、Kd的迭代結果；η2為學習速率。因此得到PID控制器的最終輸出為

(10)

3 無人艇運動模型的建立

船舶運動數學模型是船舶運動仿真與控制問題的核心，是船舶運動方程的近似。無人艇在水中航行時，通常是欠驅動的狀態(tài)，并同時進行6個自由度內的運動，包括前進、橫移、垂蕩、橫搖、縱搖和艏搖。在研究中為了達到簡化模型的目的，一般只考察平面或三個自由度內的運動規(guī)律。

3.1 船舶平面運動線性數學模型

在線性化的前提下，考慮無人艇的前進、橫漂以及轉艏運動時，船舶的運動模型為[13]

(11)

(12)

3.2 三自由度狀態(tài)空間船舶運動模型

航向保持是無人艇在執(zhí)行測繪任務的過程中的一項關鍵技術，也是影響測量準確定的關鍵因素。因此，在無人艇運動數學模型中應加入一個直觀體現的航向變量ψ，使式(13)中的狀態(tài)向量變?yōu)閇vrψ]T，因此能夠得到無人艇運動數學模型為

(13)

式(14)中:a11、a12、a21、a22、b11、b21為替代項，其具體數值可由式(13)中的參數推導得到，文獻[14]給出了無人艇運動傳遞函數的推導過程。最終獲得該無人測繪艇的響應方程為

(14)

式中：K稱為回轉性指數，用于反映無人艇的旋回特性；T為追隨性指數，可反映無人艇的航向穩(wěn)定性。

4 實例仿真分析

MATLAB中提供了一種可用于動態(tài)仿真的工具箱Simulink，這里用程序編寫RBF神經網絡的實現過程，并在程序中調用Simulink工具箱中搭建好的PID控制器，實現無人艇的航向仿真控制。為了進一步突出RBF神經網絡PID的整定效果，采用三種不同的航向控制器分別仿真。

(1)采用單一自適應PID控制器，Kp、Ki、Kd由手動調節(jié)給出。

(2)采用BP神經網絡自適應PID控制器，Kp、Ki、Kd通過前向網絡迭代獲得[15]。

(3)采用RBF-PID控制器，Kp、Ki、Kd通過程序調用S函數迭代獲得。

給定輸入航向100°，觀察系統輸出的變化。將系統的仿真時間設為2 000 s，并在第1 000 s時加入隨機擾動，考驗系統對擾動的響應能力。圖6～圖8分別顯示出了在三種不同算法控制下航向、兩螺旋槳轉速差以及系統誤差隨時間的變化。

圖6 航向-時間變化曲線Fig.6 Course-time change curve

圖7 雙槳轉速差-時間變化曲線Fig.7 Speed difference-time change curve

圖8 系統誤差-時間變化曲線Fig.8 System error-time change curve

可以看出，系統在不同算法的控制下都可以達到穩(wěn)定狀態(tài)，但是達到穩(wěn)態(tài)的時間以及系統的超調量等有很大差別。對于單一采用PID控制的系統，雖然能夠達到航向控制的要求，但是在短時間內航向和雙槳轉速差的波動非常劇烈，從而會降低無人艇的可操控性。通過BP神經網絡算法獲得的PID控制器參數，可以使系統整體的平滑性良好，對擾動也可以進行有效的糾正。但是系統在自適應算法控制下的超調量大、穩(wěn)定時間長，意味著無人艇改變航向后需要較長時間才能穩(wěn)定在新航向上，不利于航向穩(wěn)定性的保持和一些測量設備的作業(yè)。

由于RBF神經網絡在可以在局部快速逼近非線性函數的特性，采用RBF-PID算法的控制器可在短時間內迭代Kp、Ki、Kd至最佳水平，使系統的超調量為零并且使控制系統達到穩(wěn)態(tài)的時間以及對擾動的響應都非常良好。同時通過圖7可以看出，在得到一個新的航向指令后，雙推進器可以通過較小的轉速差并在較短的時間內就能將航向穩(wěn)定，反映出艇體的結構設計有利于航向的保持。圖9、圖10分別為RBF-PID控制器參數和系統雅可比值的迭代曲線。

圖9 PID參數迭代曲線Fig.9 PID parameters iteration curve

圖10 雅可比值迭代曲線Fig.10 Jacobian value iteration curve

5 結論

設計了一種雙體結構的無人測繪艇，在此基礎上利用RBF神經網絡對PID航向控制器參數進行整定。仿真結果顯示，RBF-PID控制器的性能優(yōu)于單一PID控制器和BP-PID自適應控制器，證明了RBF神經網絡結合PID算法對雙體無人艇航向控制的有效性，也為接下來無人艇的航線跟隨和自主路徑規(guī)劃研究奠定了基礎。