變截面連續箱梁剪力滯效應及其形成機制

劉青林

(中國鐵建投資集團有限公司 北京 100855)

1 引言

箱梁的剪力滯是翼板縱向彎曲正應力沿橫截面不均勻分布的現象，基于平截面假定的桿系有限元分析無法考慮這種彎曲應力的不均勻分布，從而導致應力計算結果可能偏小，因此箱梁剪力滯效應的分析和計算方法早已成為橋梁設計理論中重要研究內容之一。經過多年的研究，國內外專家學者對箱梁剪力滯的計算方法及其效應已達成諸多共識，翼板剪力滯的翹曲縱向位移可以使用二次或者三次拋物線近似描述，由此建立的剪力滯能量變分法和包含翹曲自由度的7自由度梁單元也成為剪力滯分析的主要方法和工具[1-4]；比擬桿法利用比擬桿和比擬薄板的平衡條件和位移協調條件建立微分方程，是箱梁剪力滯理論分析的主要方法之一[5-6]。趙志峰[7]等推導了單箱三室箱梁的比擬桿面積計算公式和剪力滯效應計算的控制方程，通過與有機玻璃模型試驗結果的對比，驗證了比擬桿法分析單箱三室箱梁剪力滯效應的合理性。張元海[8-9]等通過分析箱梁截面剪力流分布規律，提出了翼板縱向位移的計算公式，認為翼板剪力滯翹曲位移模式可以近似使用二次拋物線描述。肖軍[10]等基于能量變分原理推導并提出了一種針對不同余弦剪力分布的剪力滯翹曲函數，并以矩形簡支箱梁和懸臂箱梁為例，證明了其提出的方法能更好地適應不同荷載作用形式下的箱梁剪力滯效應的求解。楊綠峰[11]等針對傳統的一維離散有限元法在分析箱梁剪力滯效應方面的局限性，提出了以箱梁撓度、附加撓度及一階導數作為單元節點位移參數的一維離散元法，通過與模型試驗解以及空間有限元數值解的對比，驗證了其提出方法的合理性。馬馳[12]等基于能量變分原理推導了波形鋼腹板組合箱梁的解析解，計算結果與實測結果吻合較好。周世軍[13]等針對傳統有限梁單元法無法求解集中彎矩作用下箱梁剪力滯效應，基于能量變分原理構造了一種具有新位移模式的有限梁單元，并通過與變分法解析結果的對比，驗證了所提方法的可靠性。

能量變分法和比擬桿法在計算等截面箱梁剪力滯效應方面已有較多的研究成果，但變截面連續箱梁剪力滯效應的理論分析成果相對較少[14]，且規范中僅給出了等截面簡支梁、懸臂梁、連續梁翼板有效分布寬度取值，并未考慮截面變化對翼板有效分布寬度的影響。目前針對比擬桿的研究多以等截面簡支梁和懸臂梁展開，本文以變截面連續箱梁為研究對象，提出了變截面連續梁邊界條件的比擬桿處理方法，分析了連續梁正、負剪力滯分布規律及梁高變化對連續梁剪力滯效應的影響，加深了對變截面連續箱梁剪力滯效應的認識和理解。

2 變截面連續箱梁剪力滯效應的比擬桿法控制方程

比擬桿法將箱梁等效為承受軸力的比擬桿和承受面內剪力的比擬薄板組成的結構，每根比擬桿上軸力與兩側薄板內剪力的平衡關系滿足式(1)所示的平衡方程，比擬桿和兩側薄板的位移協調條件滿足式(2)所示的協調方程。

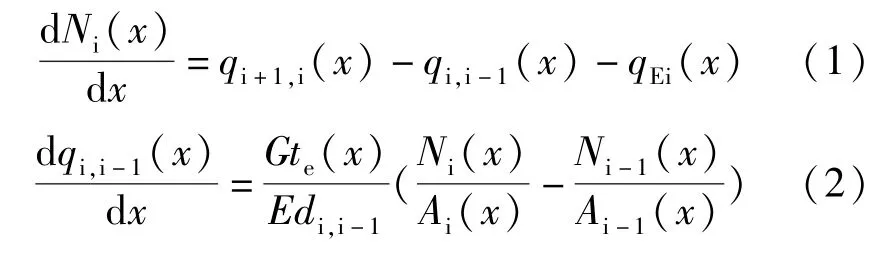
式中，下標i表示第i根比擬桿，當i-1＝0時與之相關的變量即為0；x表示橋跨位置坐標；G為剪切模量，Ni(x)、Ai(x)表示第i根比擬桿的軸力、等效面積，te(x)表示比擬薄板等效厚度，di，i-1表示頂板第i、i-1 根比擬桿之間水平距離；qi，i-1(x)表示第i、i-1根比擬桿之間薄板的剪力流和剪應變，qEi(x)表示箱梁腹板內剪力流，E為彈性模量。

對于等截面箱梁，式(2)中Ai(x)、te(x)沿跨長x不變，對式(2)兩邊求導后即可得到關于翼板剪力流的二階微分方程組，箱梁剪力滯效應的求解即轉化為翼板剪力流二階微分方程的求解。但是對于變截面箱梁而言，比擬桿等效面積將沿橋梁軸向發生變化，對式(2)兩邊求導時會產生Ai(x)、te(x)的導數，產生新的未知數，造成求解困難。為此本文參考文獻[15]的處理方法，直接將公式(1)、(2)聯立組成關于比擬桿軸力和翼板剪力流的一階微分方程組并直接求解。需要注意的是變截面箱梁內的豎向彎矩會產生附加剪應力，在求解腹板內剪力流qEi(x)必須考慮該部分附加剪應力[15]。

3 比擬桿法分析變截面箱梁剪力滯效應的合理性驗證

參考變截面連續箱梁橋常用的構造尺寸，設計一座橋跨布置為36 m＋60 m＋36 m的三跨變截面連續箱梁橋(見圖1)，梁寬25 m，梁高變化采用2次拋物線，墩頂5.0 m，跨中2.0 m，橫截面尺寸如圖2所示。梁體選用C50混凝土，建立實體有限元模型，支點處設置線約束，跨中截面采用對稱邊界。為保證求解精度，模型劃分為六面體映射網格，截面有限元網格劃分如圖3所示。

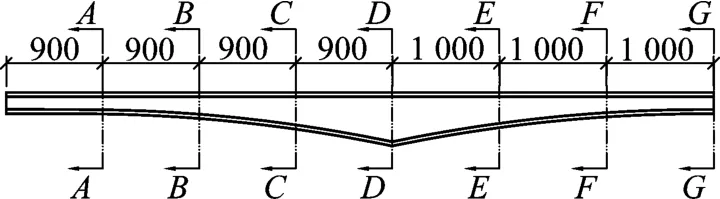
圖1 數值算例半橋跨徑布置及各截面位置(單位：cm)

圖2 數值算例橫斷面(單位：cm)

圖4給出了自重作用下三跨變截面連續梁橋不同橋跨位置處箱梁頂緣的彎曲正應力分布，從圖中可以看出本文理論解與實體有限元數值解吻合良好，證實了本文比擬桿算法在計算變截面連續梁橋剪力滯效應的可靠性。具體而言，連續梁中支點負彎矩區的D-D截面呈現正的剪力滯效應，C-C、E-E截面呈現負的剪力滯現象，靠近邊支點處的A-A、B-B截面和中跨的大部分區域均呈現正的剪力滯效應，這種現象與簡支梁、懸臂梁的剪力滯效應有所不同，這可能是由于翼緣板內水平剪切應力不均勻分布和剪應力方向的變化導致的。

圖3 箱梁截面有限元網格劃分

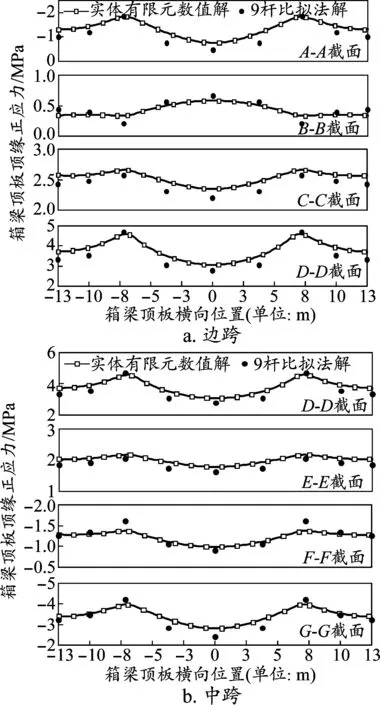
圖4 自重作用下數值算例不同位置處頂板頂緣應力分布對比

4 箱梁梁高變化對剪力滯系數的影響

為了進一步分析梁高變化對連續梁剪力滯系數的影響，以上述變截面連續梁算例為參考，設置梁高沿跨徑方向2次拋物線變化、1.5次拋物線變化、等高度2 m、等高度5.0 m等4種截面形式，對比4種工況下連續梁剪力滯系數沿跨徑方向的變化規律。

圖5中給出了4種工況下連續梁剪力滯系數沿跨徑方向的分布，從圖中可以發現，4種工況下的剪力滯系數的分布規律大致相同，在正彎矩區具有簡支梁剪力滯效應的分布特點，負彎矩區具有懸臂梁剪力滯效應的特點，即靠近約束端(中間支點)呈現正剪力滯現象，遠離約束端(中間支座)出現負剪力滯現象；連續梁正、負剪力滯交界位置大致在反彎點附近，這可能是由于反彎點附近自重彎矩及彎曲應力均接近于零所造成的；相比中跨而言，邊跨的正剪力滯效應更為顯著，但負剪力滯區段更短；箱梁截面沿橋跨方向的改變增大了正彎矩區內的剪力滯效應，而減小了負彎矩區內的剪力滯效應，另外連續箱梁梁高變化會增大梁體負剪力滯區長度，并減小正剪力滯區長度；相比于梁高的1.5次拋物線變化，梁高2次拋物線變化時連續梁橋正彎矩區剪力滯系數略大，而負彎矩區剪力滯系數略小。

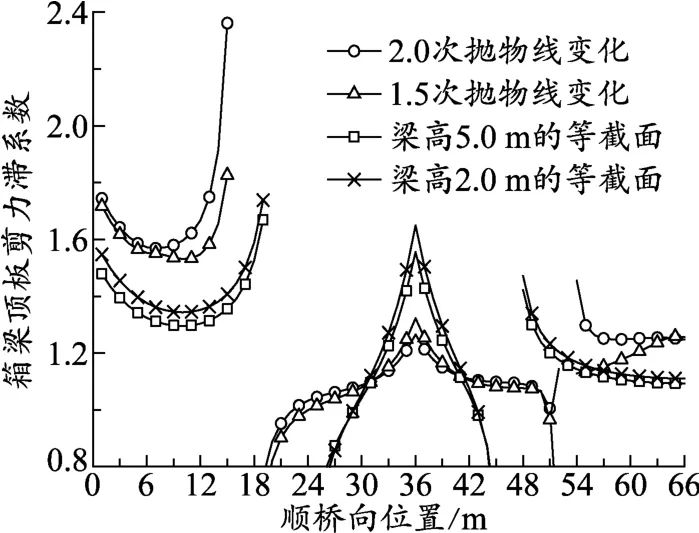
圖5 梁高變化對頂板頂緣剪力滯系數的影響

為分析和解釋上述現象產生的原因，圖6、圖7分別給出了4種截面高度變化形式下箱梁腹板剪力流qE和比擬薄板內水平剪力流q21沿橋跨方向的變化情況。從圖6中可以看出:連續梁在靠近中間支座處，梁高變化對腹板剪力流的影響與懸臂梁相似[15]，梁高從跨中向支點高次拋物線增大的趨勢與截面剪力的變化相同，減弱了箱梁腹板剪力流qE沿橋跨方向的變化梯度，且qE量值也有所減小；相反連續梁正彎矩區內梁高的高次拋物線變化反而增大了qE，這表明連續箱梁腹板內的剪力流水平及其沿橋跨方向的變化梯度可能是導致箱梁剪力滯效應的重要外因。從圖7中可以看出:中間支點截面附近的負彎矩區內，連續梁梁高的拋物線變化降低了比擬薄板內水平剪力流q21的變化梯度和幅值，而正彎矩區內連續梁梁高的拋物線變化卻增大了比擬薄板內水平剪力流的變化梯度，這表明連續箱梁頂板內水平剪力流沿橋跨方向的變化梯度可能是影響連續梁剪力滯效應的主要內因。因此如何在構造上減小連續箱梁腹板和頂板內剪力流沿橋跨方向的變化梯度，盡量讓剪力和截面的變化趨勢一致可以減小剪力流的變化梯度，進而降低連續箱梁的剪力滯效應。

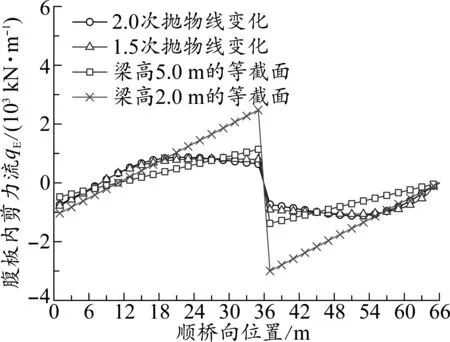
圖6 不同梁高變化形式下qE沿橋跨方向的分布

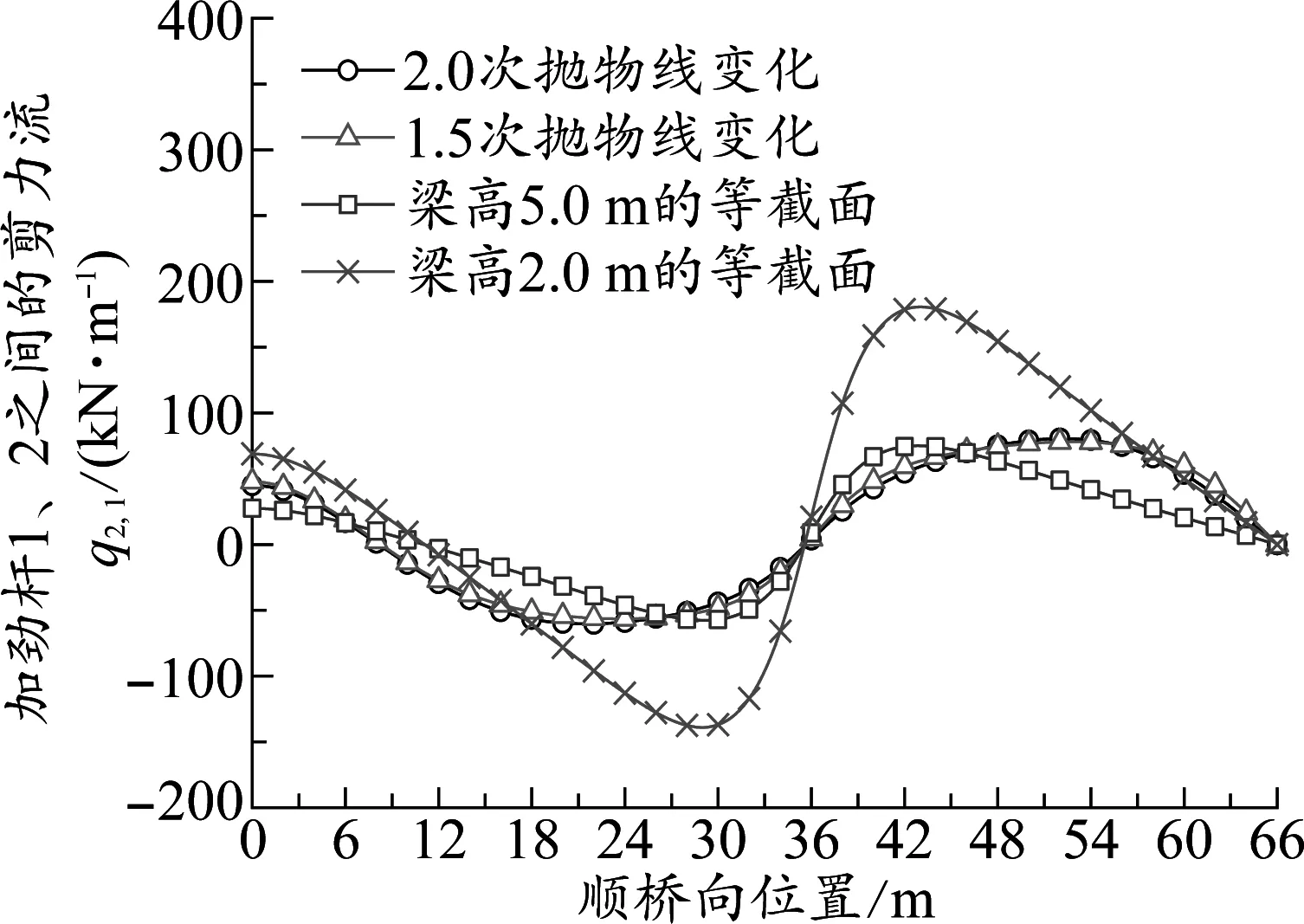
圖7 不同梁高變化形式下比擬薄板內q21沿橋跨方向分布

5 結論

(1)本文提出的變截面連續梁剪力滯效應分析的比擬桿法能正確地計算出各控制截面的剪力滯系數；

(2)連續梁正彎矩區呈現正剪力滯效應，負彎矩區的剪力滯現象與懸臂梁類似，即靠近中間支點處為正剪力滯區段，遠離中間支座處呈現負的剪力滯現象；梁高的拋物線變化會減弱連續梁負彎矩區內的剪力滯效應，但會加大連續梁正彎矩區內的剪力滯效應；

(3)工程設計時可以增大連續梁在負彎矩區梁高的變化梯度，并減小正彎矩區內梁高的變化梯度，以最大程度地減小連續箱梁的剪力滯效應。