基于改進新安江模型的巖溶地區徑流過程模擬
——以廟溝巖溶流域為例

李玉坤，燕子琪，王紀元，陳 麗，周 宏

(中國地質大學(武漢)地質調查研究院，湖北 武漢 430074)

流域水文模型是在流域產匯流結構概化的基礎上，以一個實體或數學模型來模擬流域降雨-徑流的形成過程，是一種常用的徑流過程模擬方法。流域水文模型通常分為集總式水文模型如新安江模型、SAC模型和水箱模型，分布式水文模型如SWAT模型、SHE模型，半分布式水文模型如TOPMODEL模型等。

巖溶地區含水介質內部結構復雜多樣，實測資料獲取難度較大，使得流域水文模型在該地區的應用成為難點。分布式水文模型基于水動力學機制來描述和模擬流域內的水文過程，但對資料要求較高，因而在缺乏資料地區的應用受到限制；黑箱模型又稱經驗模型，應用門檻低、適用性強，但模型不能反映含水系統內部的水文過程，也無法用于評價和管理人類活動對泉流量的影響[1]。新安江模型是一種概念模型，由于采用張力水和自由水蓄水容量曲線來描述張力水和自由水蓄水容量分布的空間異質性，因此已成為一種具有分布意義的概念性流域水文模型。近年來，隨著GIS和RS技術以及計算機的發展，新安江模型參數的精度和計算分區的精度已得到顯著提升，如李致家等[2]將新安江模型應用于柵格之上，與高精度雷達降雨資料耦合進行了洪水預報；井立陽等[3]根據地形因子分布曲線推求了自由水蓄水容量;Yuan等[4]應用雙源蒸散發模型改進了新安江模型結構，模擬了在植被參與的水循環過程中的徑流過程；Zhao等[5]將新安江模型應用于包括土壤雨水侵蝕、土地資源利用等土壤資源評價中。目前新安江模型已由功能單一的洪水預報模型發展為適用于多領域、多功能的流域水文模型。

在巖溶地區，新安江模型的應用也得到了發展。如莊一鸰等[6]在總結南方巖溶地區水文特性的基礎上，對新安江模型的穩定下滲、水源劃分和匯流模塊進行了改進，并取得了較好的模擬效果；郝慶慶等[7]在新安江模型原有自由水庫的基礎上，再增加一個線性水庫用來模擬深層地下水的出流過程，使模擬精度得到了顯著提高。但目前新安江模型在巖溶地區的應用研究仍較為有限。為此，本文選取廟溝巖溶流域為典型巖溶流域，以降雨入滲為切入點，對新安江模型進行了改進，以期提高新安江模型對巖溶地區徑流過程模擬的精度。

1 研究區概況

廟溝巖溶流域位于湖北省宜昌市興山縣黃糧鎮高陽鎮境內,為高嵐河流域的子流域，整體上處于中國大陸二級階地向三級階地過渡地帶。該流域面積約為25 km2，平均海拔為1 100 m，地貌類型為溶蝕侵蝕中山溝谷地貌。該流域西側為斜坡，巖性以志留系粉砂巖為主；東側為巖溶洼地地貌，巖性以寒武-奧陶系碳酸鹽巖為主，區內落水洞、巖溶漏斗等巖溶形態十分發育,見圖1。

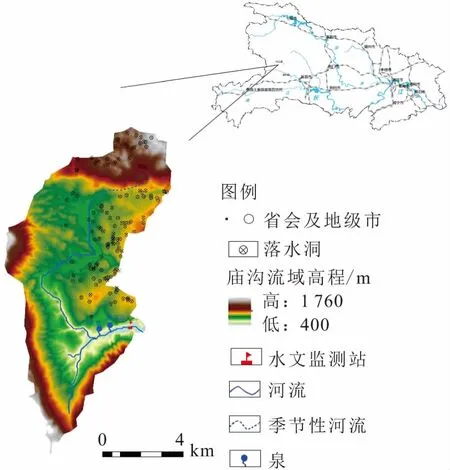
圖1 廟溝巖溶流域水系概況圖Fig.1 Drainage map of Miaogou karst basin

2 研究方法

2.1 新安江模型及預模擬

新安江模型以蓄滿產流為理論基礎，該模型結構為分散性結構。如圖2所示，降雨信號輸入模型后轉化為張力水，此時一部分水量耗于蒸散發，采用三層蒸發模型進行蒸散發計算，另一部分水量轉化為自由水，并將水源劃分為地表徑流、壤中流和地下徑流三部分；最后采用馬斯京根法進行河道匯流計算。

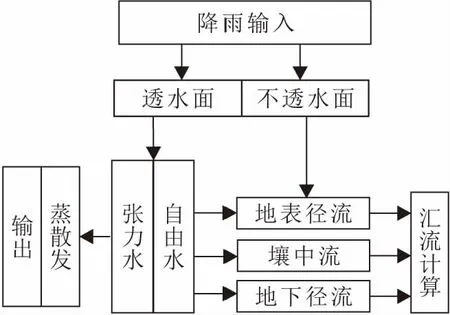
圖2 新安江模型結構簡圖Fig.2 Structure diagram of Xin’anjiang model

為了驗證原始新安江模型對巖溶流域徑流過程的模擬效果，采用原始新安江模型對廟溝巖溶流域進行了一次預模擬，選取的時間序列為2014年3月2日到2014年9月2日，期間共有4次小洪峰，1次大洪峰。原始新安江模型預模擬采用遺傳算法對模型參數進行率定，預模擬參數率定值見表1，預模擬的效果圖見圖3。

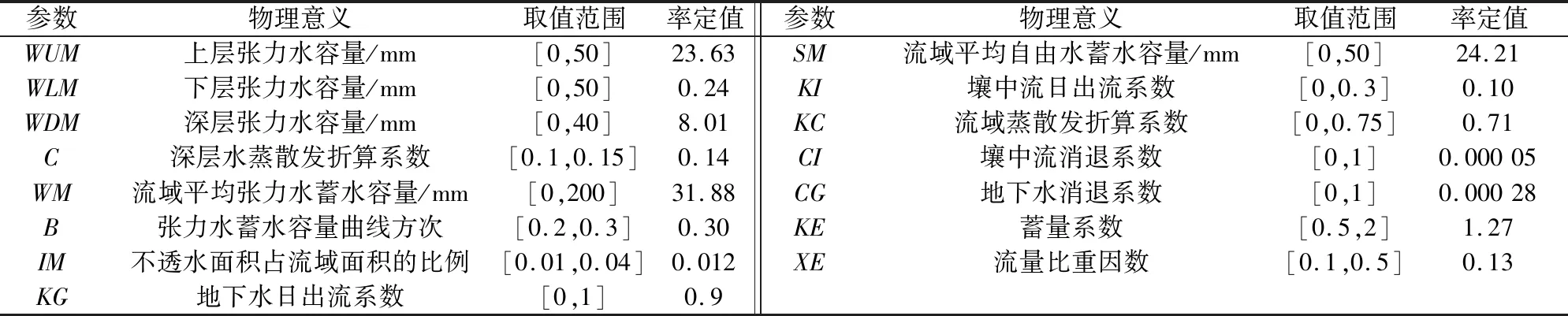
表1 原始新安江模型預模擬參數率定值[8]Table 1 Pre-simulation parameters of the original Xin’anjiang model[8]

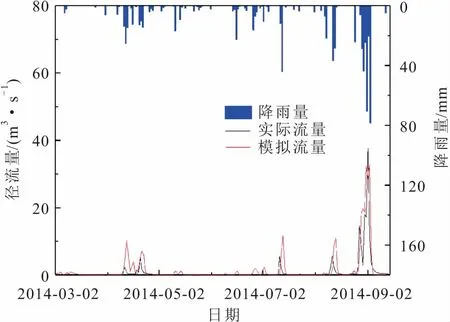
圖3 原始新安江模型預模擬的效果圖Fig.3 Pre-simulation results of the original Xin’anjiang model

從原始新安江模型預模擬的結果可以發現以下現象：

(1) 根據賈云飛等[9]對金沙江流域張力水蓄水容量的研究，一般流域平均張力水蓄水容量WM取值范圍在90～150 mm之間，而預模擬的WM值為31.88 mm，與經驗值相比偏小。

(2) 模擬流量對降雨的響應過于敏感，多大于實際流量，即使無效降雨，模擬值也會有所響應。

(3) 模擬洪峰流量較為滯后，起峰過程長，退水過程短，峰形較寬緩，拖尾現象不明顯。

結合廟溝巖溶流域的水文地質條件，對上述現象分析如下：

非巖溶地區降雨降至地面之后，經過緩慢入滲至地下水，這一過程在原始新安江模型中體現為三層蒸散發模型和表層、下層、深層3個串聯張力水水庫的計算，因此該模型對降雨信號的過濾能力強，較好地模擬了非巖溶地區含水介質對降雨的調蓄功能。而在巖溶地區，降雨經過地表產流通過巖溶管道直接匯入地下，相對于非巖溶區，巖溶區降雨在地表和淺層土壤滯留的時間更短，匯入地下轉化為地下水的速度更快，效率更高，所以巖溶地區地下水對降雨的響應更為迅速，退水也更為迅速。因此，將新安江模型直接應用于巖溶地區徑流過程的模擬會造成以下兩個結果：①加長了洪峰的響應時間，導致模擬洪峰流量較為滯后；②減小了流域平均張力水蓄水容量WM值和自由水蓄水容量SM值，減小了產流閾值，縮短了模擬值的響應時間。這將導致模擬結果對降雨的響應過于敏感、拖尾現象不明顯。

2.2 新安江模型的改進

Hartmann等[10]認為，流域的巖溶發育程度越高，滲透性能越好。而巖溶地區降雨主要通過洼地、落水洞等巖溶地貌直接灌入并補給地下水，因此等效于降雨中的一部分受包氣帶調蓄，參與蒸發過程，另一部分直接補給地下水(見圖4)。故本文根據新安江模型預模擬的結論，將直接補給地下水的一部分降雨量定義為P1，總降雨量為P2，則參與蒸發過程的降雨量為P2-P1，并定義了降雨分配系數φ：

(1)

郭緒磊[11]、羅明明[12]的研究表明，南方巖溶地區地下水降雨入滲系數多在0.07～0.7之間，故本文中φ的取值范圍為0～0.7。

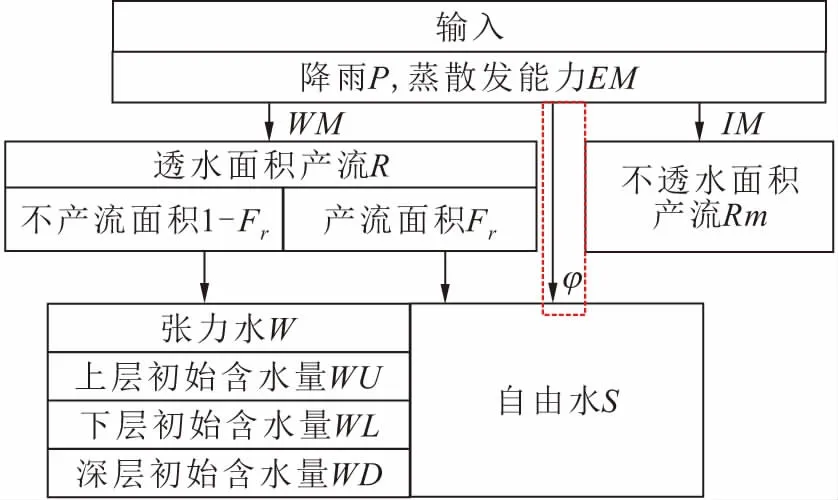
圖4 降雨-自由水轉換結構示意圖Fig.4 Schematic diagram of rainfall-free water transition

另外，在地下徑流(RG)出流之前，增加一個線性水庫用以模擬深層溶洞水(快速徑流)與裂隙水(慢速徑流)的水量交換過程(見圖5)，進入快速流水庫和慢速流水庫的水量由巖溶管道和裂隙的發育情況決定[7]。

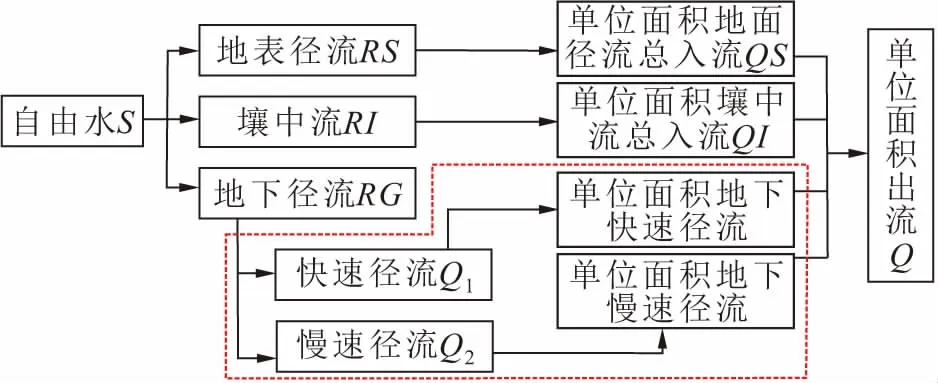
圖5 溶洞快速和裂隙慢速徑流結構示意圖Fig.5 Schematic diagram of fast runoff in karst caves and slow runoff in fracture

溶洞快速徑流流量和裂隙慢速徑流流量的計算公式如下:

(2)

式中：Q出，1、Q出，2分別代表快速徑流和慢速徑流的出庫流量(m3/s)；Q入，1、Q入，2分別代表快速徑流和慢速徑流的入庫流量(m3/s)；α1、α2分別為溶洞水和裂隙水的地下水衰退系數。

2.3 模型參數的敏感性分析

原始新安江模型改進后共涉及17個參數，其中φ、α1和α2為新增參數。本文首先采用One-factor-At-a-Time(OAT)法對模型參數進行局部敏感性分析。參數的敏感系數Si表達式為

(3)

式中:x為參數變化量;y為因變量模擬流量；Si為參數的敏感系數即敏感度，其大小代表敏感性的強弱。

改進的新安江模型各參數取值同表1，模型參數的敏感度Si計算結果及其排序見表2[13]，模型參數敏感性分類見表3。

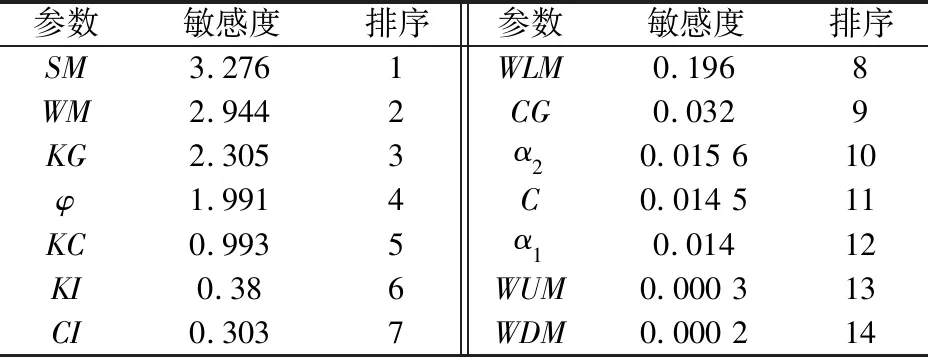
表2 改進的新安江模型參數敏感度及其排序Table 2 Sensitivity of parameters of the improved Xin’anjiang model and the ranking

注：敏感度較低的模型參數未列出。

表3 改進的新安江模型參數敏感性分類Table 3 Classification of the sensitivity of parameters of the improved Xin’anjiang model

結合表2和表3可知，改進的新安江模型參數SM、WM、KG和φ為極敏感參數，KC、KI和CI為敏感參數。其中，張力水蓄水容量WM和自由水蓄水容量SM均屬于模型中線型水庫的出流閾值，WM控制產流，SM控制自由水水量，影響水源劃分，兩者直接影響著模型中水量的轉換，參數的敏感性較高；地下水出流系數KG控制著自由水S中地下水的出流比例，對于Nash-Sutcliffe效率系數DC有著十分顯著的影響[14]，因而參數的敏感性較高；降雨分配系數φ描述了通過巖溶管道直接灌入地下轉化為自由水的部分降雨，實質上該參數減少了水分蒸發量，并將減少的水分直接轉化為自由水，減小了模型對降雨的調蓄作用，使得模擬徑流對降雨的響應更加迅速，而這一點恰恰與巖溶地區的產流特點相吻合。

2.4 φ值對巖流流域徑流過程模擬的影響分析

為了進一步探究參數φ值對巖溶流域徑流過程模擬效果的影響，本文針對廟溝巖溶流域140831號洪峰流量，利用改進的新安江模型對其進行了模擬，分析不同φ值對巖溶流域徑流過程模擬效果的影響，并與參數SM值和WM值進行比較，其模擬結果見圖6。其中圖6(a)、(b)、(c)分別為只改變φ、SM、WM參數時，廟溝巖溶流域洪峰流量模擬曲線與實際流量曲線的對比圖。

由圖6(b)、(c)可見，隨著參數SM、WM的增大，模擬洪峰流量整體上逐漸減小，強降雨和弱降雨的模擬流量的“平均流量水平”逐漸降低。

表4為不同敏感參數取值時模擬得到的廟溝巖溶流域洪水信息統計表。

由表4可知，當WM值逐漸增大時，平均流量、洪峰流量和確定性系數DC值逐漸減小，流量誤差逐漸增大；當SM逐漸增大時，平均流量、洪峰流量和DC值逐漸增大，流量誤差逐漸減小，但當SM取值大于80 mm時，DC值和流量誤差分別保持在96.4%和19.78%；在參數φ值逐漸增大的過程中，各項指標均符合先增大后減小的規律，并且當參數φ取值為0.5時，巖溶流域徑流過程的模擬效果達到最優。

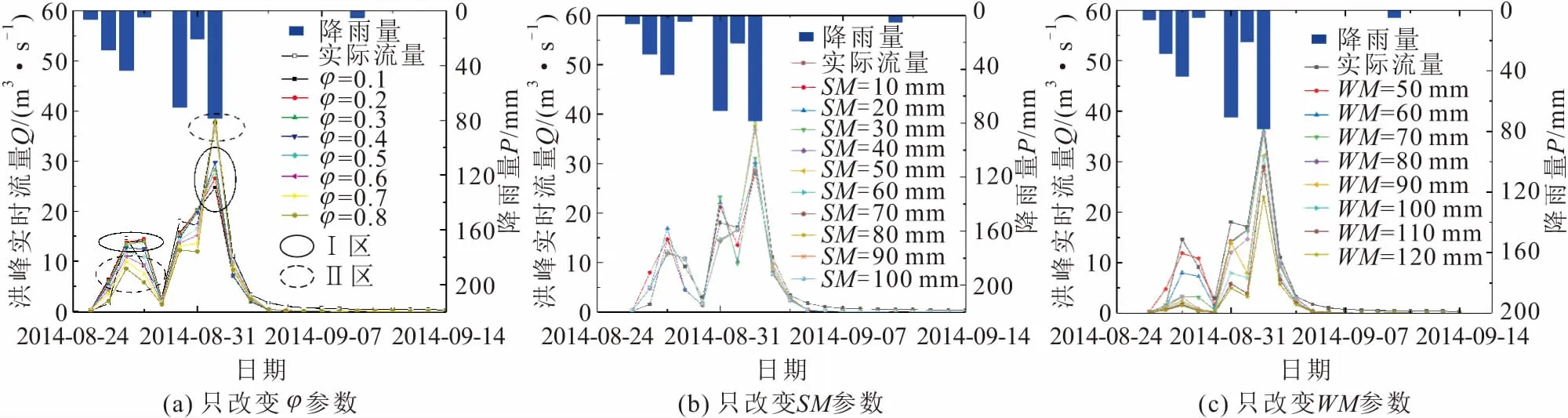
圖6 不同敏感參數取值時廟溝巖溶流域洪峰流量模擬曲線與實際流量曲線的對比圖Fig.6 Comparison between simulated and actual curves of runoff process in Miaogou karst basin with different sensitive parameter values

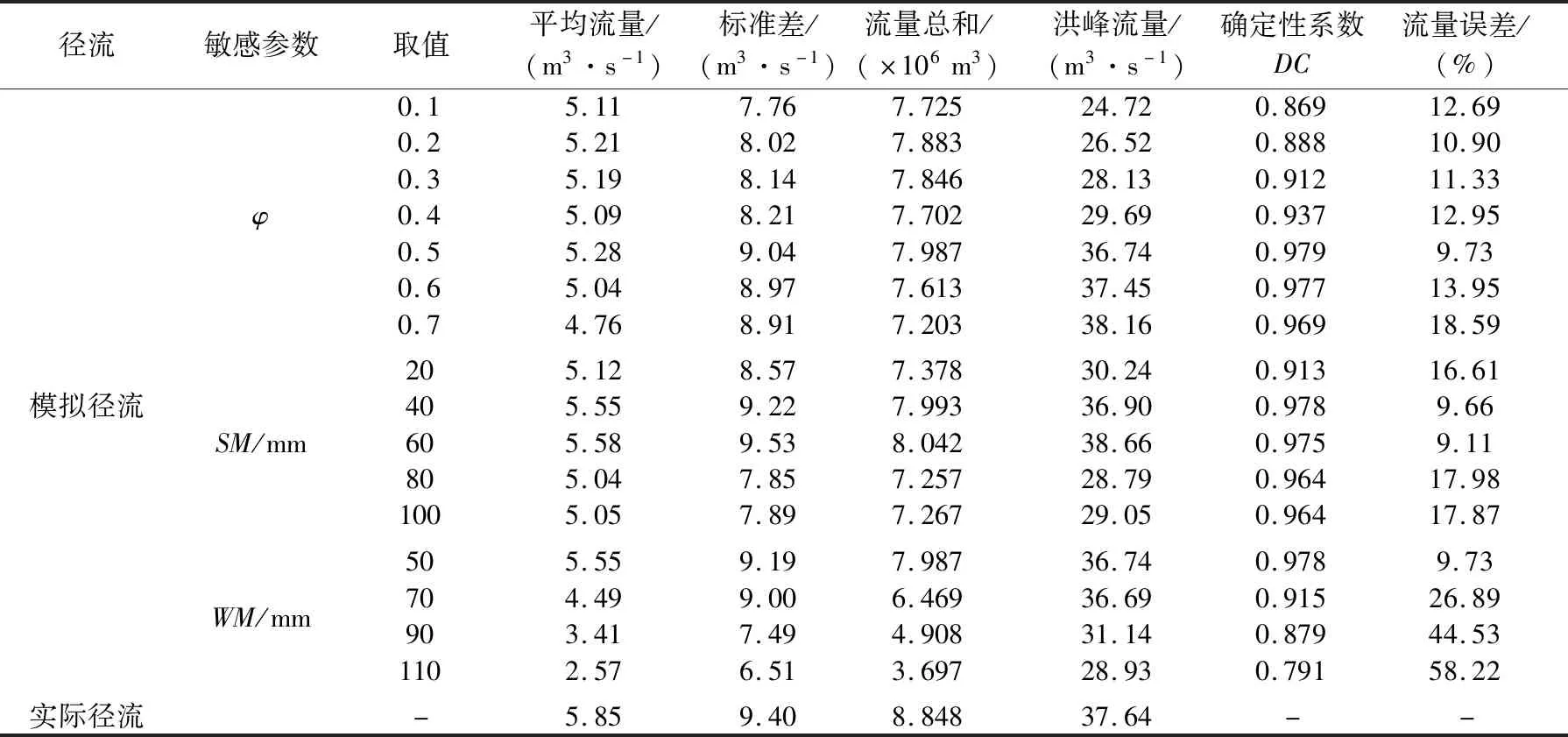
表4 不同敏感參數取值時模擬得到的廟溝巖溶流域洪水信息統計表Table 4 Statistical table of simulated flood information of Miaogou karst basin with different sensitivity parameter values

由此可見，WM值控制模擬流量的“平均流量水平”，影響模擬流量的縱向“高度”，決定著模型模擬效果的整體水平；SM為自由水蓄水容量，向下由地下水日出流系數KG控制地下水徑流，壤中流出流系數RI控制壤中流，當自由水量大于SM值時，出流成為地表徑流RS，而巖溶地區地表徑流成分較小，因此當自由水量大于SM值時，SM值的大小不會改變模型的模擬效果，DC值和流量誤差保持穩定。

結合圖6(a)可以發現，當參數φ值較小時，洪水峰值更多落在圖中Ⅰ區，較小洪峰流量的模擬效果較好，較大洪峰流量的模擬效果較差，改進新安江模型對強降雨的響應效率較低，模擬效果更接近于原始新安江模型；隨著參數φ值的增大，弱降雨模擬洪峰流量逐漸減小，強降雨模擬洪峰流量逐漸增大，洪水峰值逐漸由Ⅰ區向Ⅱ區過渡；當參數φ值較大時，洪水峰值主要落在Ⅱ區，較小洪峰流量的模擬效果較差，較大洪峰流量的模擬效果較好，說明改進新安江模型對強降雨的響應效率更高。整體上模擬值的“平均流量水平”變化幅度相對較小。表4中數據也表明，參數φ值在整個取值域中流量誤差的變化范圍在3%以內，而SM值和WM值在整個取值范圍內誤差的最大變化范圍分別為7.5%和48.5%。

3 模型應用與分析

3.1 模型參數率定

南方地區蒸散發折算系數KC一般取0.6，上層初始含水量WU、下層初始含水量WL和深層初始含水量WD是比較重要的指標，其值的大小可以看作是整個流域內蓄水量變化的起點，直接影響后期模型參數率定的準確度以及模型模擬的效果[15]。

流域平均張力水蓄水容量WM可用實測資料分析，即選擇前期特別干旱的一次全流域產流過程進行分析，根據廟溝巖溶流域實際降雨資料，確定WM取值為50 mm。利用2014年3月2日——2014年9月15日降雨徑流數據作為改進的新安江模型參數率定期，采用遺傳算法對模型參數進行率定，最后確定了Ⅰ區和Ⅱ區改進新安江模型的參數，見表5。

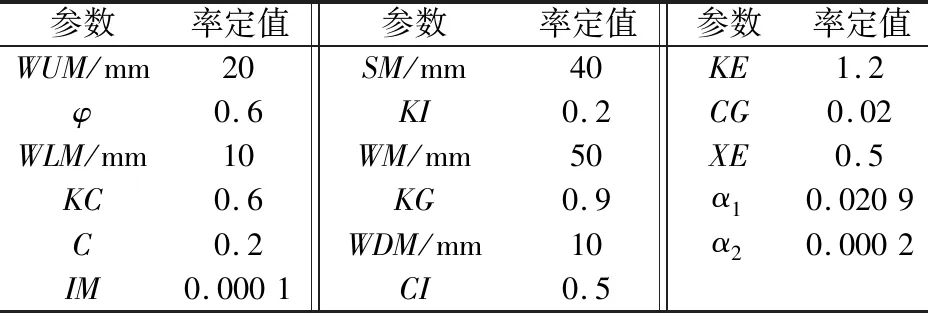
表5 改進的新安江模型參數率定值Table 5 Parameter values of the improved Xin’anjiang model

3.2 模擬結果與分析

根據參數率定表確定的改進新安江模型參數，對Ⅰ區和Ⅱ區改進的新安江模型分別賦值并計算2014年3月1日—2014年12月1日的降雨徑流，其模擬結果見圖7,模擬結果的精度見表6。

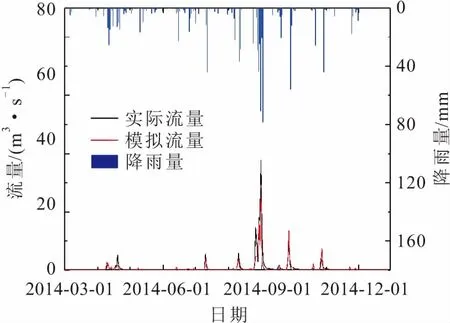
圖7 模擬徑流量與實際徑流量的關系圖Fig.7 Diagram of the relationship between simulated flow and actual flow

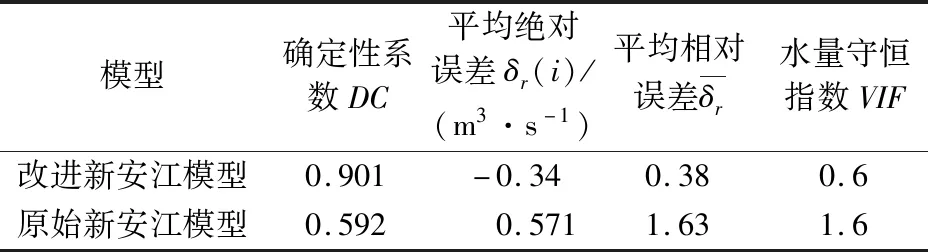
表6 新安江模型模擬精度評定表Table 6 Simulation accuracy evaluation table for Xin’anjiang model

由圖7可見，改進的新安江模型的模擬效果較好，所模擬的洪峰起峰時間及峰值均與實際洪峰過程較為吻合。由表6可知，改進后新安江模型模擬結果的確定性系數DC由0.592增長至0.901，平均絕對誤差和相對誤差均有較大幅度的減小。總體上看，改進的新安江模型模擬值偏小，從而導致水量平衡偏小。

為了探究改進的新安江模型對廟溝巖溶流域洪峰過程的模擬效果，利用改進的新安江模型針對廟溝巖溶流域2014年4月10日、2014年7月14日、2014年8月13日以及2014年8月31日4次小洪峰過程進行模擬，并分析模型參數對改進新安江模型模擬效果的影響，其模擬結果見圖8和表7。

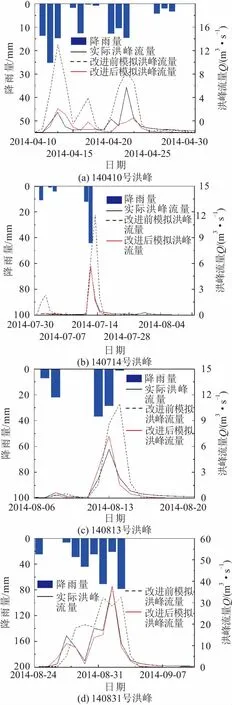
圖8 廟溝巖溶流域4次洪峰徑流過程模擬結果與實際流量的對比圖Fig.8 Comparison between the simulated and actual runoff during the runoff process of four flood peak periods in Miaogou karst basin

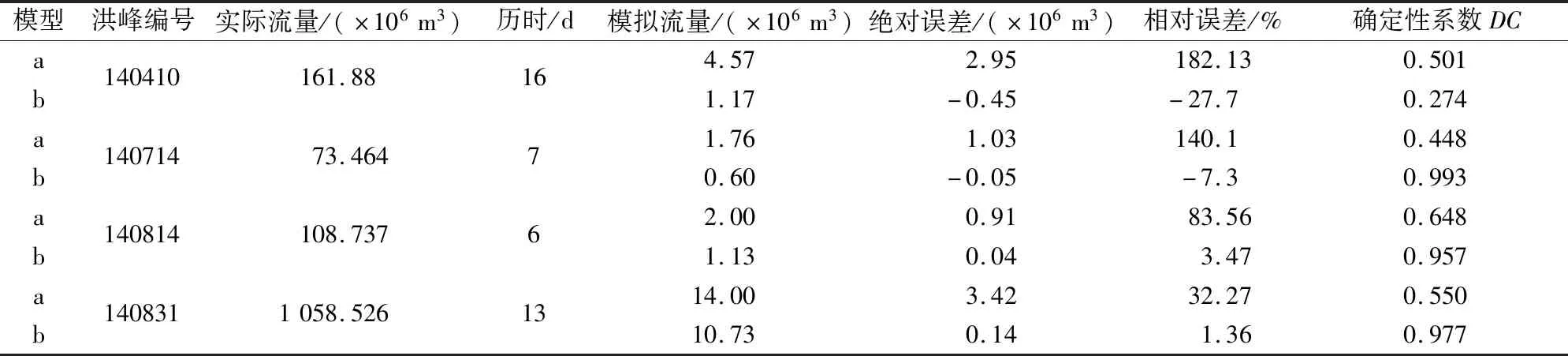
表7 廟溝巖溶流域4次洪峰徑流過程模擬值與實際值信息表Table 7 Information table of simulated runoff and actual runoff in the runoff process of four flood peak periods

注：a為原始新安江模型；b為改進的新安江模型。

由圖8和表7可見，改進新安江模型的確定性系數明顯優于原始新安江模型，140410號洪峰可能是由于降雨-流量的相關關系較差，故而其模擬的效果較差。

4 結 論

(1) 原始新安江模型直接應用于巖溶地區徑流過程的模擬效果較差，本文根據巖溶地區降水灌入并補給地下水的特點，對原始新安江模型入滲模塊結構進行了調整，增加了降雨-自由水直接轉換環節，改進后新安江模型模擬結果的確定性系數由0.592增為0.901，單次徑流過程模擬精度最高可達0.993。

(2) 降雨分配系數φ實質上將部分降雨直接轉化為自由水，減少了包氣帶對降雨的調蓄時間，縮短了模擬徑流對降雨的響應時間，提高了新安江模型降雨-徑流的轉化效率。

(3) 降雨分配系數φ的敏感度為1.991，在新安江模型眾多參數中排在第4位，僅次于SM、WM和KG參數，且該參數更側重于改變確定性系數DC值，對模擬流量的影響較小。

綜上所述，改進的新安江模型對廟溝巖溶流域徑流過程的模擬效果有顯著提升。