一組合幾何問題的證明和推廣

孫 泰

(北京市豐臺區第二中學 100071)

2017年8月10日晚，華南師范大學吳康教授在朋友圈發帖，公布數學家楊路教授在朋友圈發布征求一個幾何命題的初等證明的帖子：

命題一個平面凸四邊形，經過每三個點可作一個圓，這樣得到4個圓(不排除其中有重合)，求證：4個圓中如果有3個相等，則此4頂點共圓.

帖子發出，迅速得到余澤偉老師、朱斌老師、李榮峰老師、駱來根老師及本人的解答.

本題簡潔優美，證法多樣，余味不絕，遂探究推廣，幸得點滴，下以示之，望得指點.

引理1若△ABC和△ABD外接圓是等圓且不重合，則C、D在AB同側時，∠ACB+∠ADB=180°；C、D在AB異側時，∠ACB=∠ADB.

(如圖1)由同圓或等圓中，等弧所對應的圓周角相等，及圓內接四邊形對角互補容易得之.

引理2△ABC三個頂點與點D構成平面凸四邊形，若△ABD、△ACD與△ABC外接圓相等，則A、B、C、D四頂點共圓.

證明分兩種情況.

情況1：(如圖2)若△ABD、△ACD與△ABC外接圓相等且不重合，否則A、B、C、D四頂點共圓.

由引理1知∠ADB+∠ACB=180°, ∠ADC=∠ABC,且∠ADB<∠ADC，于是∠ABC+∠ACB>180°，那么與△ABC內角和等于180°矛盾，必有A、B、C、D四頂點共圓.

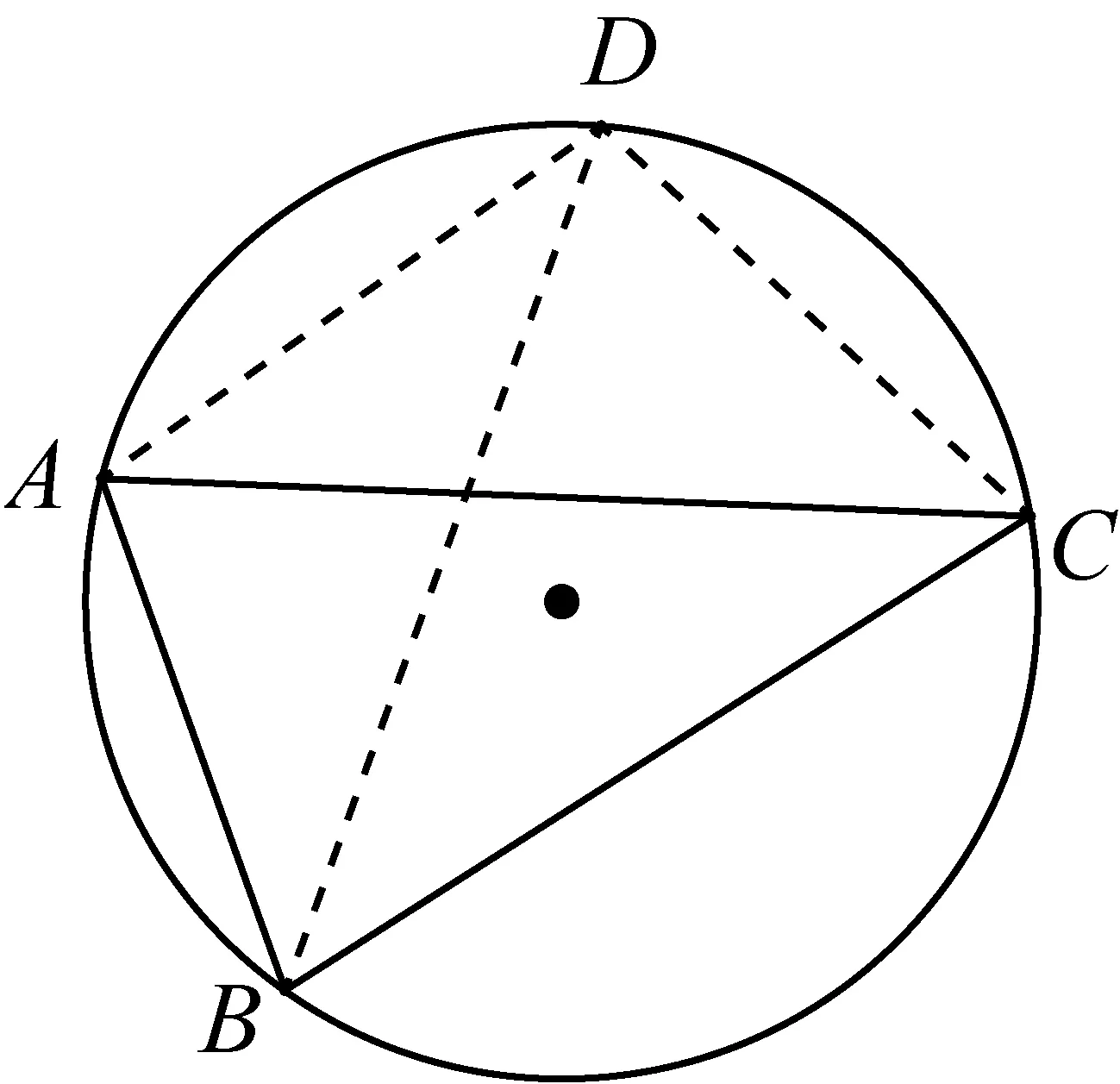
圖2

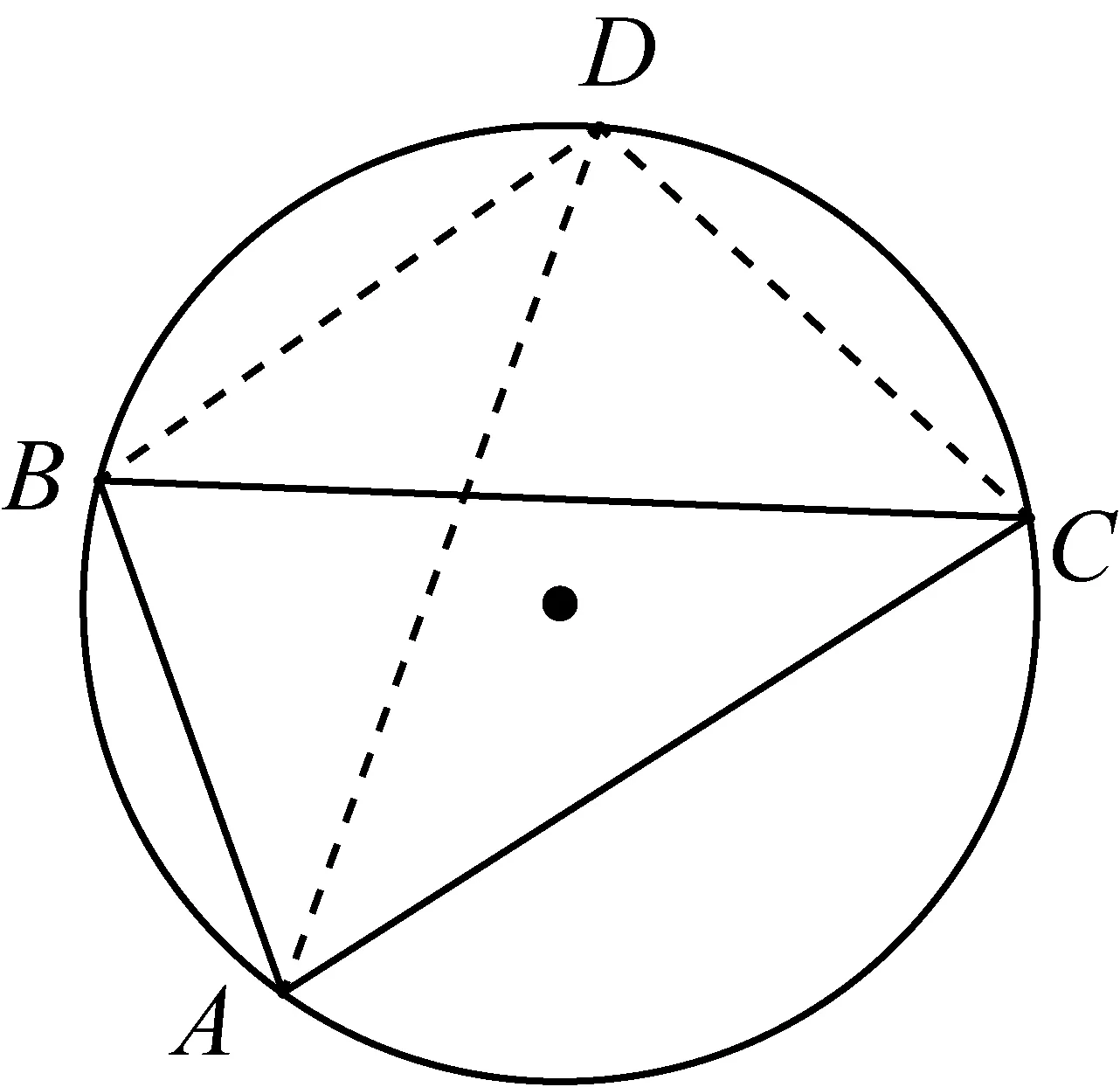
圖3

情況2：(如圖3)若△ABD、△ACD與△ABC外接圓相等且不重合，否則A、B、C、D四頂點共圓.

由引理1知∠ADB+∠ACB=180°, ∠ADC+∠ABC=180°，那么凸四邊形ABCD內角和必大于360°，與平面凸四邊ABCD不符，必有A、B、C、D四頂點共圓.

注：此引理等價于楊路教授提出的命題.

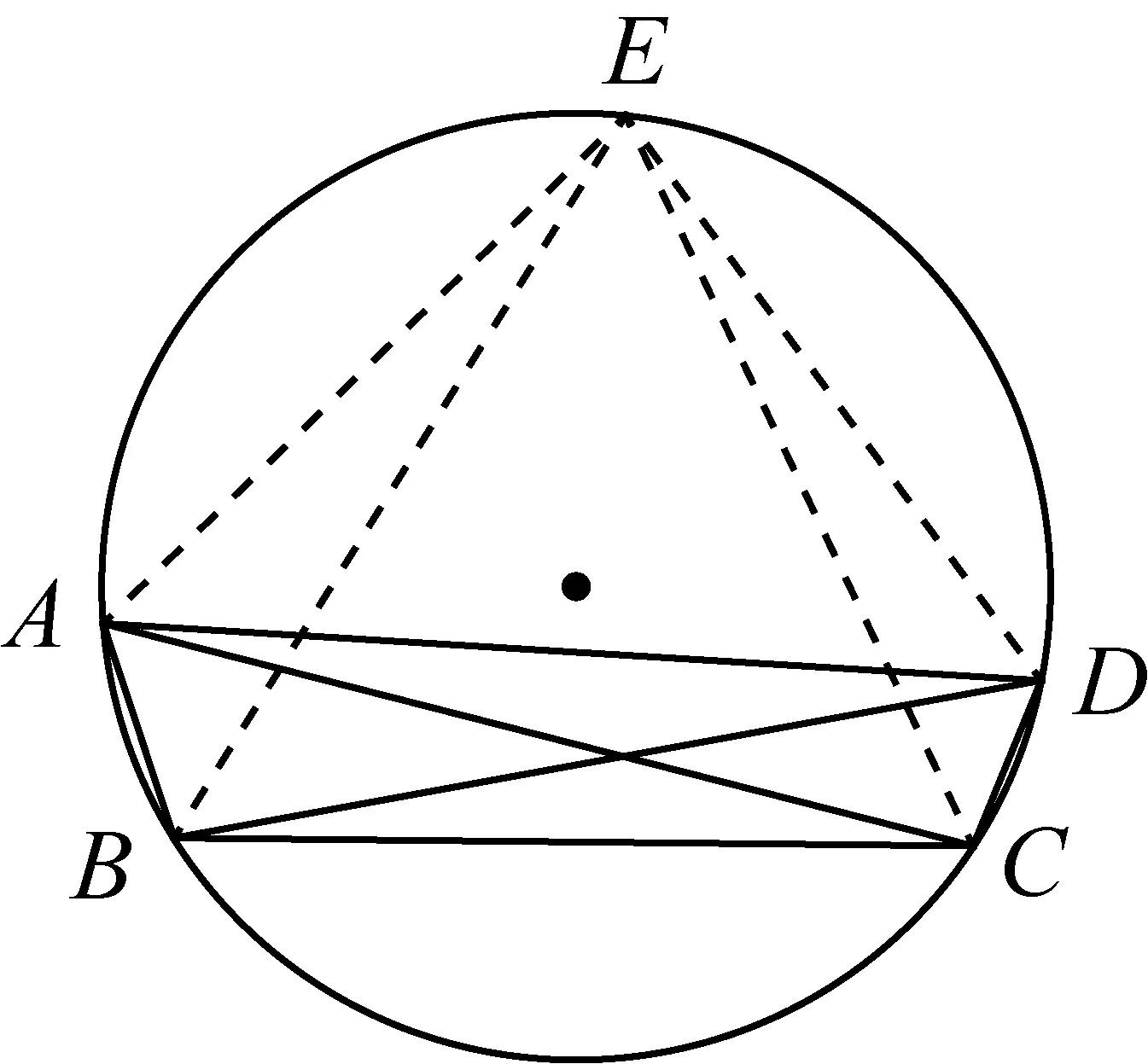
圖4

引理3如圖4,⊙O內接四邊形ABCD與點E構成平面凸五邊形ABCDE，若△ABE、△ACE外接圓與⊙O相等，或若△ABE、△CDE外接圓與⊙O相等，或若△BCE、△ADE外接圓與⊙O相等，則A、B、C、D、E五頂點共圓；若△ACE、△BDE外接圓與⊙O相等,A、B、C、D、E五頂點未必共圓.

證明情況1：△ABE、△ACE外接圓與⊙O相等，由引理2知A、B、C、E四點共圓，則A、B、C、D、E五頂點共圓；

情況2：(如圖4)若△ABE、△CDE外接圓與⊙O相等，假設△ABE、△CDE外接圓與⊙O相等且不重合，由引……