點幾何理論與GeoGebra實踐①
張志勇 羅建宇
(1.江蘇省常州市第五中學213001;江蘇省張家港市沙洲中學215600)
我們知道,解析幾何是用代數方法研究幾何問題,思路清晰有章可循,但代數方法在計算過程中很難看出幾何意義,于是為尋求能夠更直接處理幾何問題的代數方法,數學家們開辟了“幾何代數”領域.張景中先生等建構的“點幾何”理論,用簡明的概念、平常的符號和代數運算的形式描述幾何對象之間的關系,不僅符合數學直觀,也能更方便地表達基本幾何事實,而且有助于幾何推理的簡捷化[1][2].GeoGebra作為一款“專為教與學的動態數學軟件”,內嵌有計算代數系統和指令輸入方式,可對幾何對象進行直接代數化處理,從而實現“形”(幾何Geometry)與“數”(代數Algebra)的完美融合.巧合的是,GeoGebra的很多指令規則與點幾何理論完全一致,可以說GeoGebra就是點幾何理論的一個實踐場.應用點幾何理論于GeoGebra實踐中,既是對理論的支持驗證,也有助于軟件的理解把握.
1 點的線性運算
點幾何中定義了“點加點”和“數乘點”,即A+B=(xA+xB,yA+yB)、λA=(λxA,λyA);以此為基礎,推導出兩點線性組合uA+vB=tP的意義和uA+vB=rC+sD的表示,特別地,直線上任意一點都可以表示成P=tA+(1-t)B,△ABC平面上任意點P=xA+yB+(1-x-y)C.
GeoGebra支持點的線性運算.如圖1,在指令輸入框中輸入“A+B”、“-2A”,得到D、E兩點;輸入“(A+B)/2”、“(A+B+C)/3”,得到線段AB的中點F和三角形ABC的重心G;輸入“B-A+C”,可構造平行四邊形ABHC的第四個頂點H.值得說明的是,GeoGebra有很好的幫助功能,如查看代數區中的坐標,可以發現D=(xA+xB,yA+yB)、E=(-2xA,-2yA);而圖1右側的作圖過程,可查看每一個點的屬性;另外A、B、C為給定的初始點.
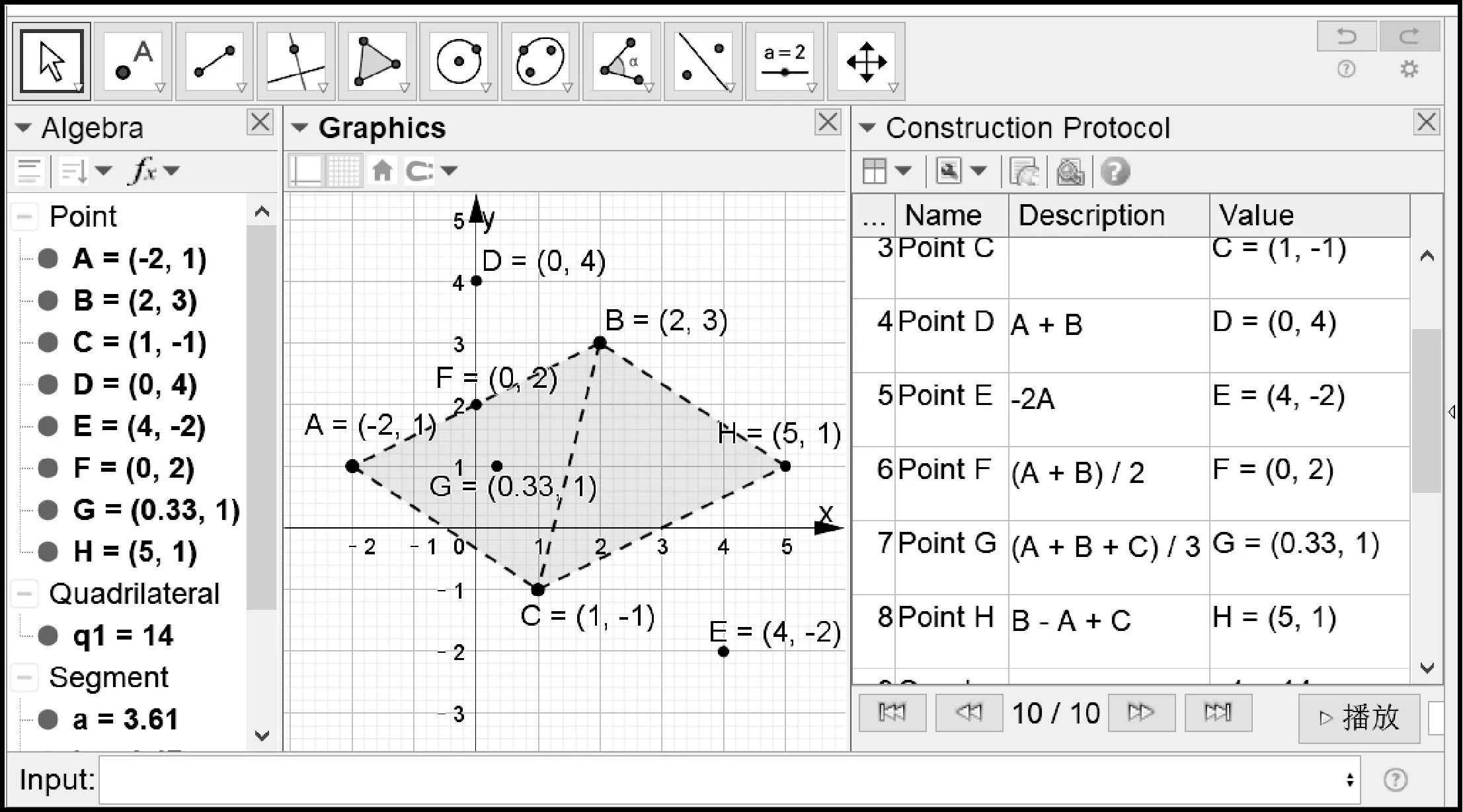
圖1
擴展開去,可通過語句“P=x*A+y*B+(1-x-y)*C”的輸入,來構造△ABC平面上任意一點P;……

