基于ARIMA 模型的未知觀測噪聲協方差矩陣的卡爾曼濾波技術

邢思遠，張 遜，徐國亮

(江蘇自動化研究所，江蘇 連云港222061)

0 引 言

雷達量測數據可以看作是1組有序、隨機的時間序列數據[1]，此數據實際是由目標真值和量測誤差綜合組成。對該量測時間序列的一種處理方法是時間序列分析法。這種方法通過序列自身建立可以直觀體現出觀測數據序列與噪聲序列之間關系的模型，再進一步利用此模型進行分析和研究[2-3]。在某些工程中，存在著無法精確獲得觀測噪聲矩陣的情況，而根據經驗選取的觀測噪聲矩陣值的準確性將直接影響到標準卡爾曼濾波方法的性能，最嚴重的后果就是狀態估計發散而徹底無法工作[4]，這種情況下研究未知觀測噪聲協方差矩陣的卡爾曼濾波方法是很有必要的。本文主要工作就是解決這一問題。通過構建時間序列模型，在此基礎上推導未知觀測噪聲協方差矩陣的遞推式，并用于標準卡爾曼濾波中進行狀態濾波。經過建模仿真實驗驗證，取得了良好的效果。

1 建立時間序列模型

t時刻的序列可以通過公式表示為：

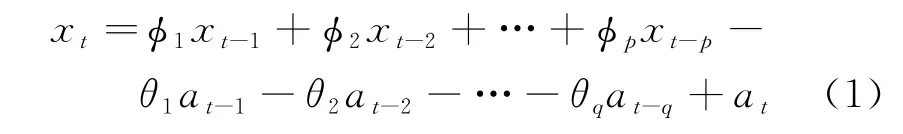
式中：φi(i=1，2，…，p)為自回歸(AR)參數；p為AR 的階數；θj(j=1，2，…，q)為滑動平均參數，q為MA 的階數；{a t}之一序列為白噪聲序列。

式(1)稱為{x t}的自回歸滑動平均模型[5]，記為ARMA(p，q)模型。

ARMA 模型處理的數據要求是平穩的，但在實際的雷達測量中，數據通常是非平穩的。處理方法是通過數據差分除去序列中的趨勢項，直到序列平穩為止。對于該處理后的平穩數據先進行ARMA建模[6]，再根據差分的次數計算出差分算子，最后反向得到原始序列的時間序列模型，即自回歸和滑動平均(ARIMA)模型。

所以，對于非平穩時間序列模型，ARIMA 模型可表示為：

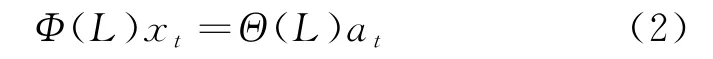
其中：

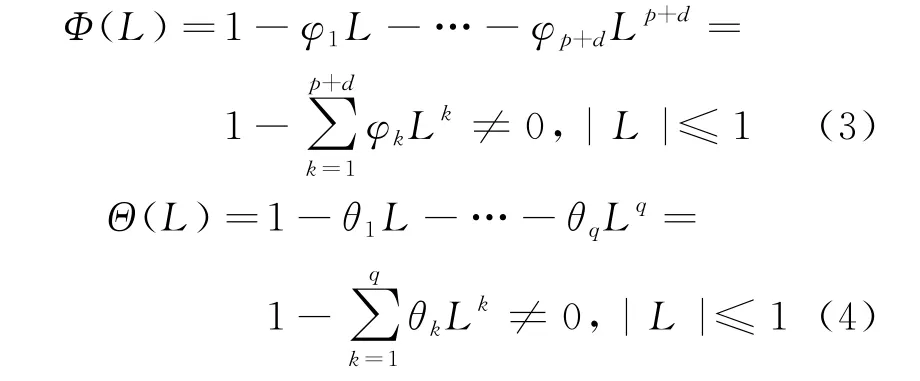
式中：p、q意義與式(1)中相同；d為差分階數；L為后移算子，滿足Lx k=x k-1。

與式(1)相比，式(2)包含d階差分算子?d=(1-L)d，在處理非平穩數據時，通過將d階差分算子作用于原始序列{x t}，獲得平穩的時間序列{x′t}。通過對平穩時間序列建立ARMA(p，q)模型，可以得到原始非平穩時間序列的ARIMA(p，q，d)模型[7]。

對于{x′t}建立的ARMA 模型Φx′t=Θa t，通過令x t=?d x′t，得到關于原始非平穩時間序列的ARIMA 模型Φx t=Θa t，即Φ?d x′t=Θa t。至此，非平穩時間序列的處理過程可以分成3步：

(1)通過差分運算求得原始序列的差分后平穩序列，并得到差分階數d；

(2)對處理后的平穩序列進行ARMA 建模，得到ARMA(p，q)模型；

(3)通過差分算子，求取原始序列的ARIMA模型，ARIMA(p，q，d)。

其中關鍵步驟是求取ARMA 模型，從過程x的N次觀察中估計ARMA 模型需要3個步驟：

(1)確定ARMA 模型的類型，為AR、MA或ARMA 模型；

(2)階數選擇：確定模型階數、參數數量；

(3)參數估計：確定模型的參數模型φi和θj。

具體建模流程如圖1所示。

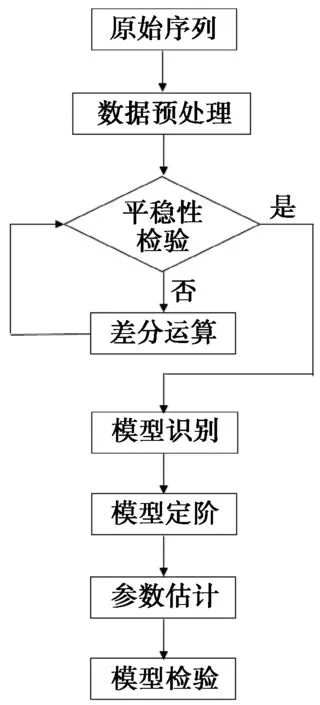
圖1 建模流程框圖

通過上述分析可知，原始序列是非平穩時間序列，數據預處理即是對數據的差分處理過程，直到滿足平穩性檢驗。令序列{x′t}表示經過差分處理之后的平穩時間序列[2]。

平穩性檢驗中采用Daniel方法假設檢驗。做出如下假設：H0表示序列平穩，H1表示序列非平穩。取統計量如下：

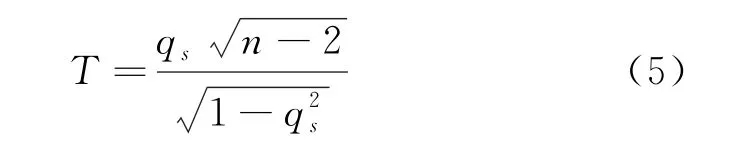
當‖T‖≤tα/2(n-2)時，接受H0假設。若序列非平穩，則對該序列繼續做差分運算。經過d階差分后，得到平穩時間序列[8]。

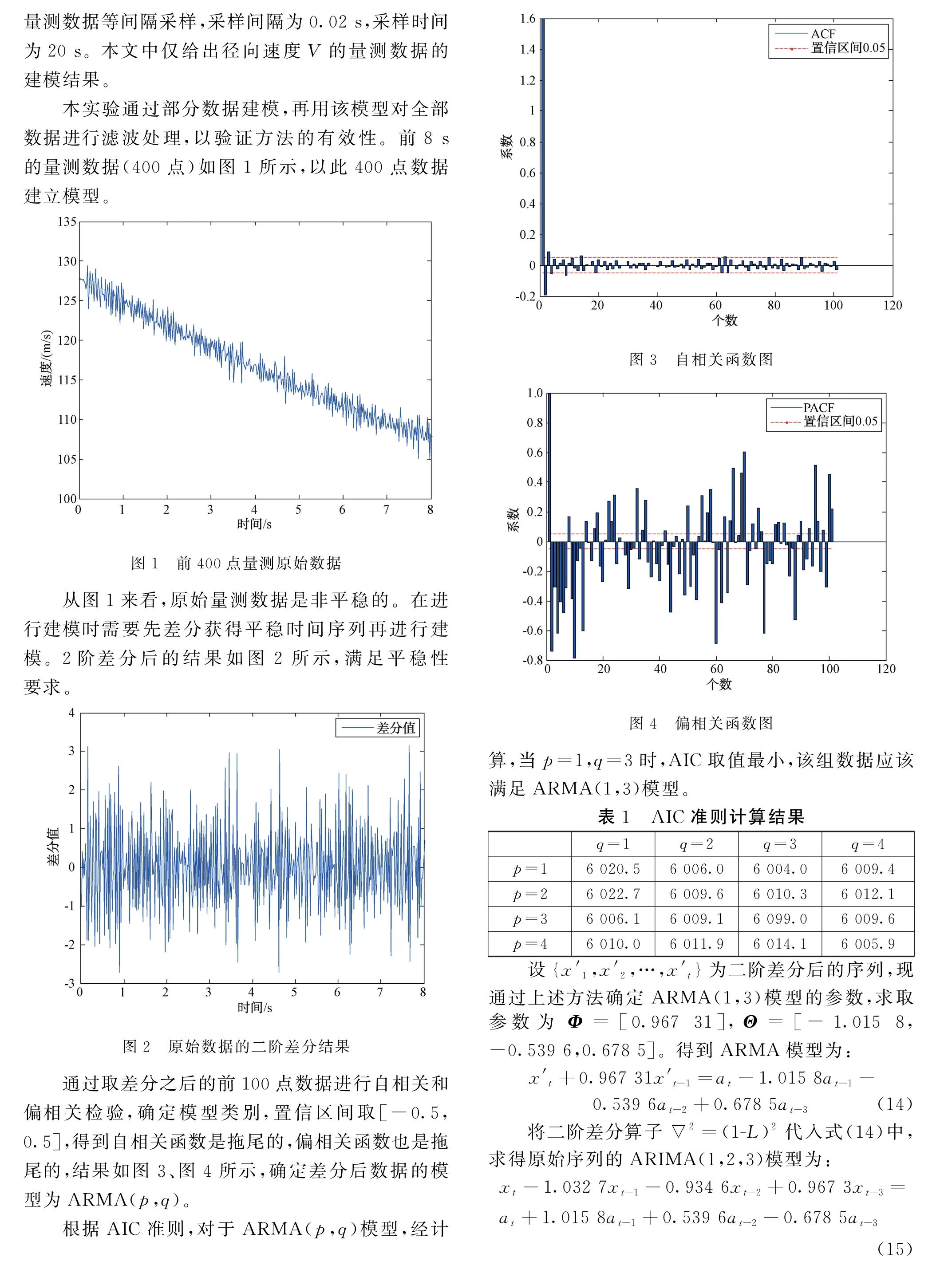
即：

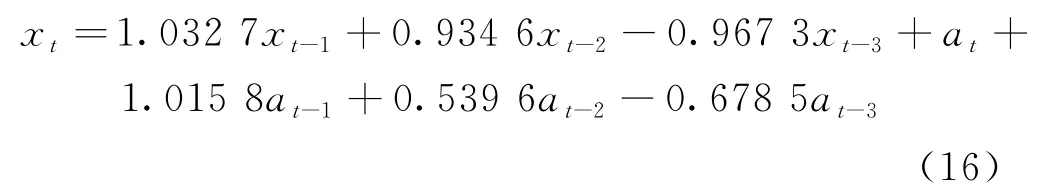
根據式(16)建立卡爾曼濾波模型，可以得到

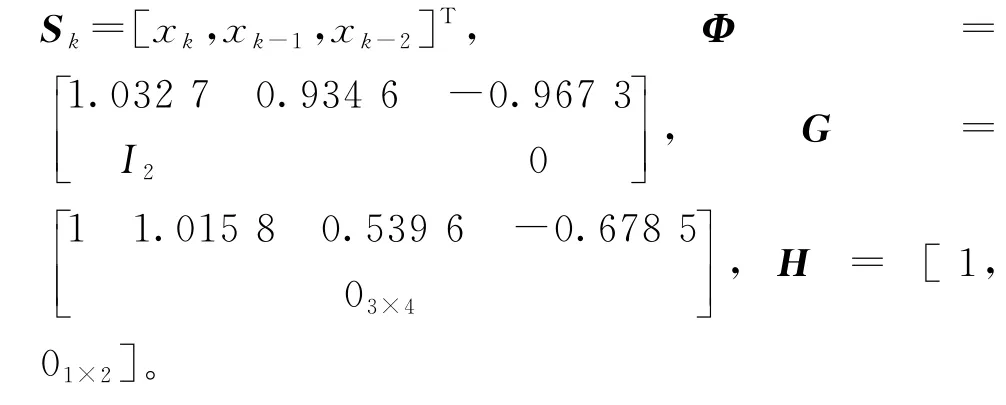
本方法中觀測噪聲協方差矩陣的初始值取值條件是不能為零矩陣，同樣地，取值越接近真實值濾波收斂的速度越快。本實驗中，協方差矩陣取小值，通過圖4的實驗結果可以看到，經過約0.2 s的濾波震蕩之后，開始收斂到真值附近。

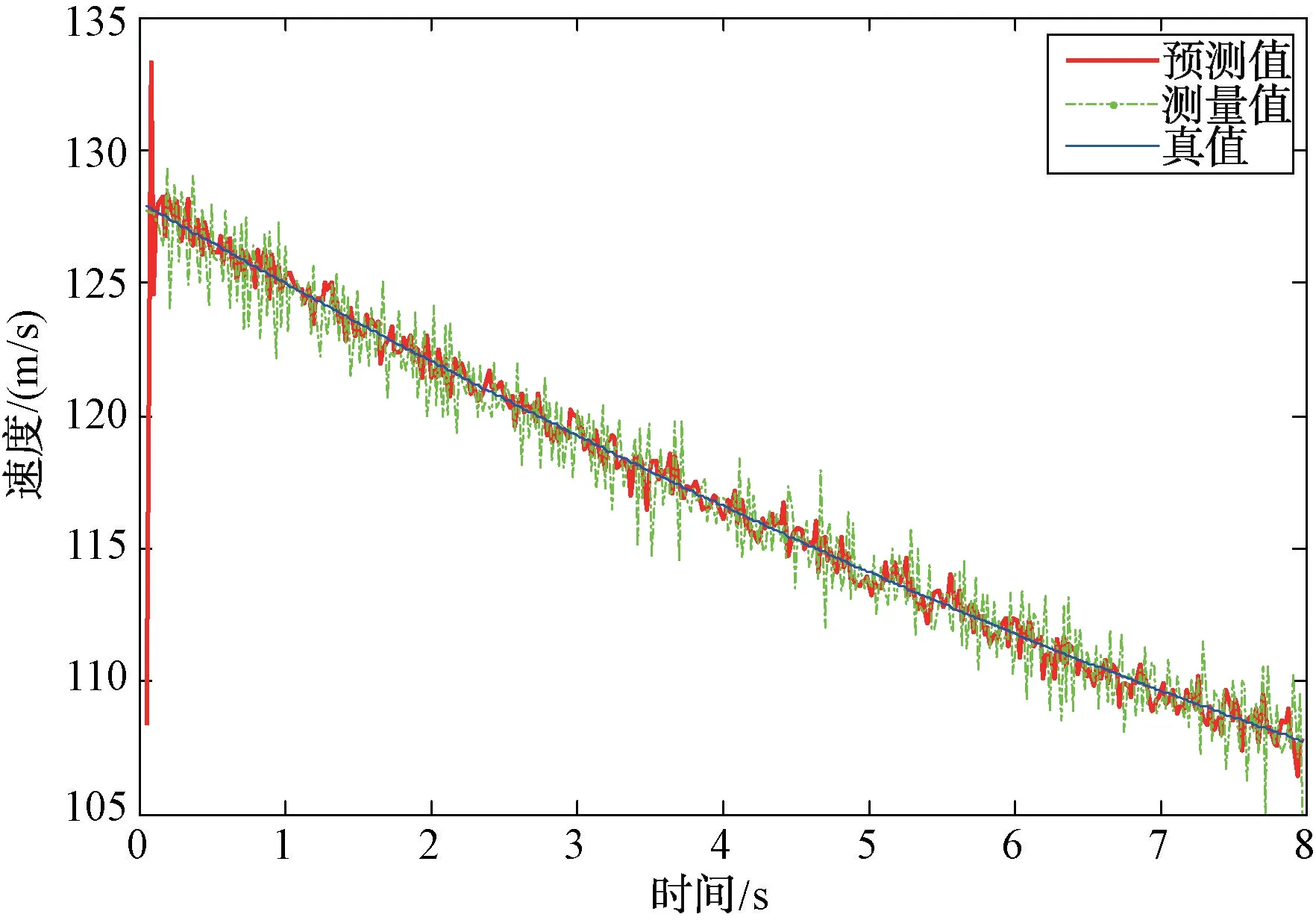
圖4 測量值與預測值結果圖

將該模型應用于仿真中剩余的數據，為查看方便，去除濾波未收斂部分，得到圖5結果。

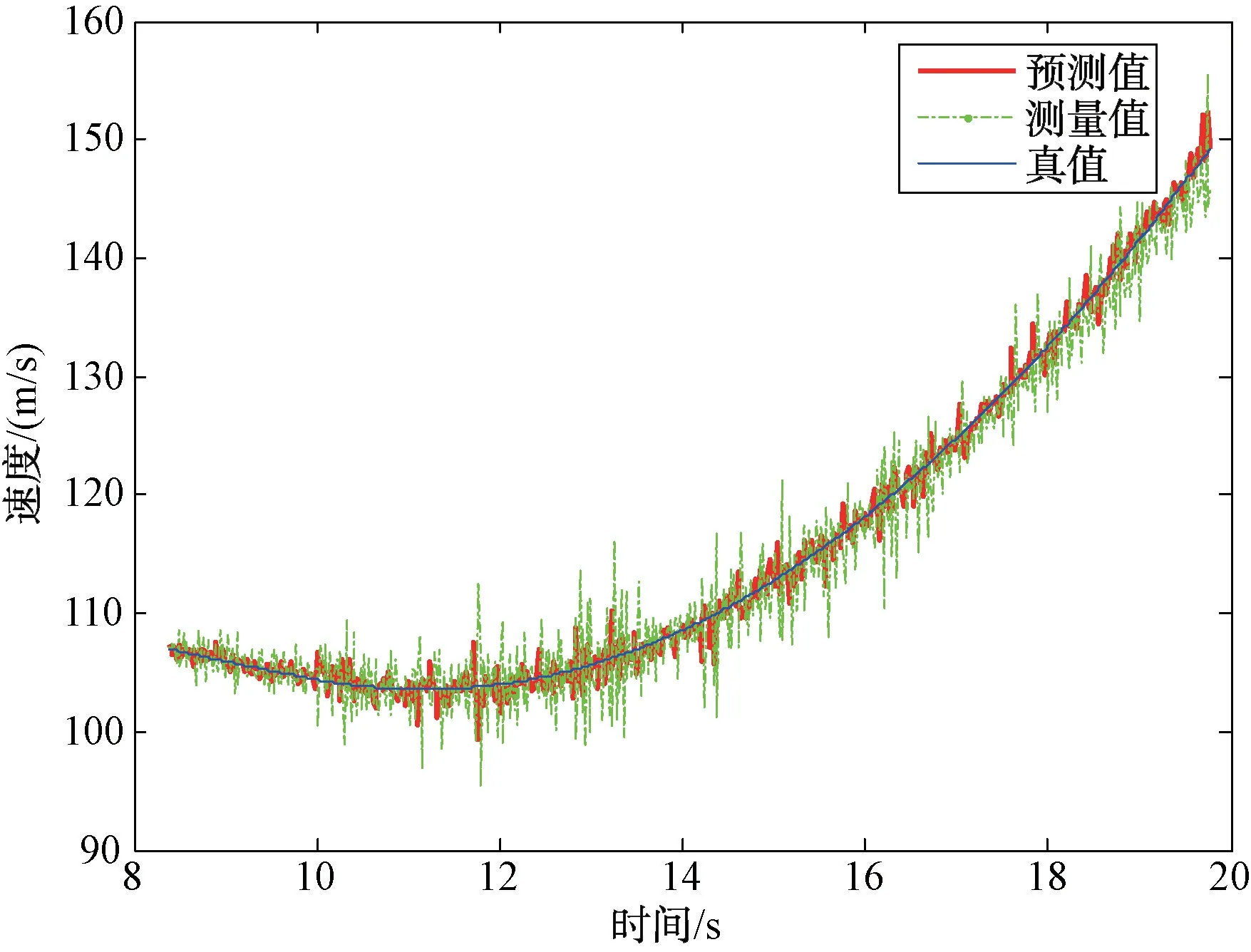
圖5 剩余數據濾波結果

從圖4與圖5可以看出，經過此方法濾波之后的數據要比測量數據更接近真值，在真值附近小幅度震蕩，隨機誤差得到了抑制。通過差分剔除趨勢項后，求得濾波前后隨機誤差方差如表2所示。

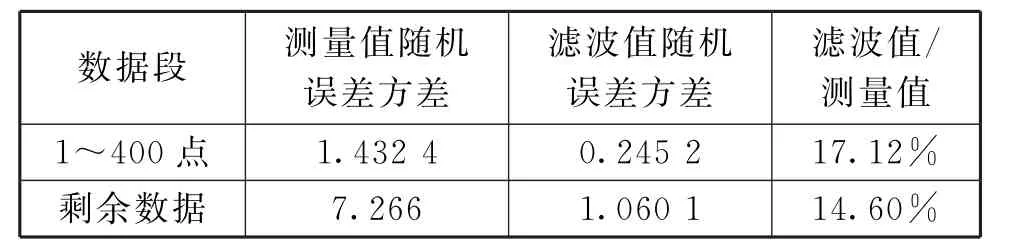
表2 量測數據濾波前后隨機誤差方差統計(m/s)

從表2可以看出，對于前400點量測數據，量測值隨機誤差方差為1.432 4，經過建模、濾波之后降到了0.245 2，隨機誤差方差為原始的17.12%；余下數據通過建立的模型進行濾波之后，誤差方差為原始數據的13.60%，誤差得到了大的抑制。

4 結束語

本文首先通過平穩時間序列建立了ARIMA 時間序列模型，其次推導出觀測噪聲協方差的遞推公式；然后將建立的時間序列模型應用于未知觀測噪聲協方差矩陣的標準卡爾曼濾波。利用前400點有限數據所設計的濾波器對所有數據進行隨機誤差濾波處理，濾波后的誤差分別為原始數據的17.12%和14.60%。數據結果表明：本文提出的基于ARIMA 模型的未知觀測噪聲協方差矩陣的標準卡爾曼濾波能有效地抑制隨機誤差，可以有效地進行數據預測，具有實用意義，對未知觀測噪聲協方差矩陣的卡爾曼濾波有較大的應用價值。