扭轉梁式光纖光柵加速度傳感器分析與設計

周海陽 趙振剛 于 虹 姚 敏

（1.昆明理工大學信息工程與自動化學院；2.云南電網有限責任公司電力科學研究院）

在交通系統、建筑形變、電網輸電及航天器狀態監測等領域［1～4］，為了避免微小損傷長時間累積后造成實際危害，必須重點對工程的健康程度持續監測，盡早處理潛在問題，防止發生事故。 加速度信號測量是工程中常用的一種技術手段。 加速度傳感器通過接收振動參數，不僅能直觀地反映出物體的振動狀態，還可以提取出位移、速度等其他振動特征量，用于健康監測或是故障診斷［5］。 光纖光柵加速度傳感器由于質量輕、體積小、抗電磁干擾能力強且安全性能高而得到廣泛研究和應用［6］。

目前，國內外研究者根據光纖光柵加速度傳感器的原理設計了不同形式的扭轉梁式結構。 王宏亮等研制的光纖布拉格光柵振動傳感器采用了對稱式的雙等強度懸臂梁， 能夠得到可靠的振動信號， 諧振頻率為80.74Hz， 加速度靈敏度約為20.85pm/g［7］。 美國伊利諾伊大學的Talebinejad I等研究了一種基于等強度梁結構的FBG加速度傳感器，諧振頻率為150Hz，而靈敏度只有12.95pm/g［8］。在此基礎上，Basumallick N等經過進一步研究，通過調整光纖傳感器軸到懸臂中軸的距離， 使加速度傳感器的靈敏度比文獻［7］的設計增大了約兩倍，提升到了45.90pm/g，而諧振頻率只有十幾赫茲［9］。 在光纖光柵加速度傳感器的設計中，傳統梁式結構普遍存在傳感器靈敏度值提高會降低諧振頻率、諧振頻率提高會降低靈敏度值這一現象。

筆者提出了一種基于扭轉梁式結構的光纖光柵加速度傳感器。 首先理論分析了扭轉梁結構的加速度信號檢測原理，接著根據仿真結果再對結構參數進行調整提高其性能，最終能夠實現在適當增大加速度傳感器靈敏度值的同時不降低諧振頻率范圍，可檢測高頻信號。

1 扭轉梁光纖光柵加速度傳感器

1.1 光纖光柵傳感理論

根據光纖光柵的耦合模理論［10］，光纖光柵由于波導與光波相互作用，使光纖中傳輸的光波從原來限定在纖芯中前向傳輸的模式耦合，變為限定在包層或纖芯中前向或后向傳輸的模式，從而得到特定的透射和反射光譜特性。 寬帶光若滿足布拉格條件，光纖光柵會將它反射回來，不滿足條件的光則全部投射出光柵［11］。

光柵的布拉格波長λB可由下式確定：

式中 neff——纖芯有效折射率；

Λ——光柵周期。

由式（1）可知，纖芯有效折射率neff和光柵周期Λ是影響光纖光柵反射波長的兩個因素。Λ的改變可以通過外界應力產生的壓縮或拉伸作用實現。 在變化的應力作用下，布拉格波長隨之變化，可用下式進行描述［12］：

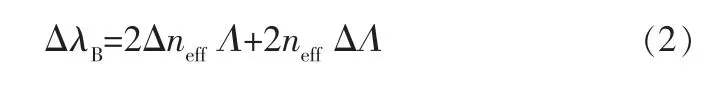
式中 ΔλB——光柵的布拉格波長變化量；

Δneff——纖芯有效折射率改變量；

ΔΛ——光柵周期改變量。

當應變施加在光纖光柵上時，光纖光柵的中心波長隨應變大小不同發生相應變化。 將信號解調后，可獲取中心波長變化量，經過運算后得到加速度信號。

1.2 傳感器結構及原理

扭轉梁式結構的光纖光柵加速度傳感器主要組成部分有：扭轉圓盤、扭轉梁、質量塊，傳感器結構如圖1所示。 主體是有一定厚度的扭轉圓盤，圓盤上緊貼質量塊，在扭轉圓盤的外圍貼有一根處于繃緊狀態的光纖光柵。

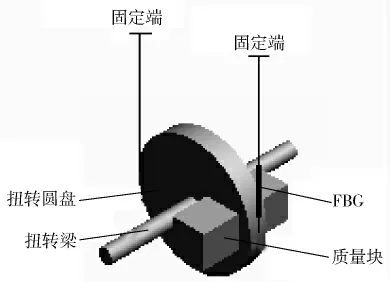
圖1 扭轉梁式光纖光柵加速度傳感器傳感模型

當有外力施加于傳感器上時，在扭轉圓盤上質量塊的帶動下， 扭轉梁產生微小的扭轉形變量， 而與之相連的扭轉圓盤能將這一微小量放大，扭轉圓盤外圍的光柵受到的拉力大小隨扭轉量變化而改變。

截面扭矩T計算公式如下：

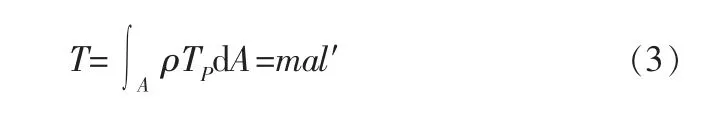
式中 a——質量塊轉動角加速度；

A——截面面積；

l′——慣性力臂；

m——質量塊質量；

TP——截面扭矩；

ρ——質量塊距圓心的距離。

截面扭矩等于慣性力矩［13］，即：

式中 G——切變模量；

x——圓盤兩側距離；

γP——切應變；

φ——扭轉角度。

將式（4）代入式（3）中得截面扭矩為：

式中 IP——橫截面極慣性矩。

因此，截面扭矩T可簡化成：

設扭轉梁長度為l，扭轉圓盤半徑為R，則扭轉角度φ為：

光纖光柵所受應變ε為：

式中 l光——光纖光柵的柵區長度。

諧振頻率f為：

式中 J ——轉動慣量。

將質量塊等效視為扇形體，質量塊、扭轉梁、扭轉圓盤的轉動慣量分別為J1、J2、J3，即：

式中 h1——質量塊厚度；

h2——扭轉圓盤厚度；

r——扭轉梁半徑；

r1——質量塊到扭轉梁中心內圈半徑；

r2——質量塊到扭轉梁中心外圈半徑。

總轉動慣量為J=J1+J2+J3。

2 扭轉梁光纖光柵加速度傳感器有限元分析

2.1 初始結構參數仿真

利用ANSYS軟件對扭轉梁式結構的光纖光柵加速度傳感器進行有限元仿真分析，以獲得不同結構下的物理特性。 仿真流程如圖2所示。

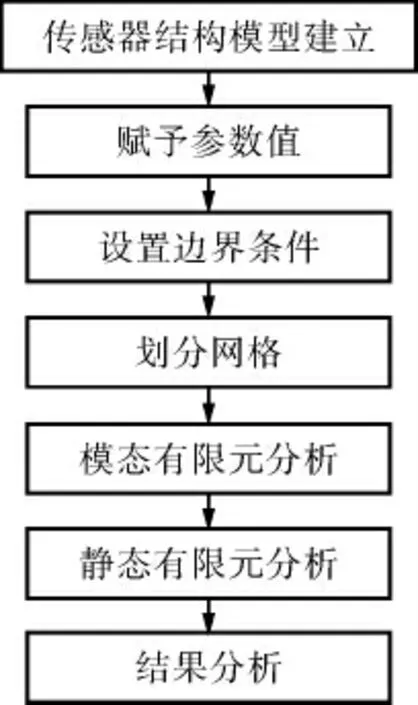
圖2 仿真流程

影響傳感器性能的參數主要有：扭轉梁的直徑和長度，扭轉圓盤的直徑和厚度，質量塊的內徑、外徑、角度及高度等。 對傳感器進行模態有限元分析和靜態有限元分析，初始結構參數如下：

扭轉梁

半徑r 1.5mm

長度l 21mm

扭轉圓盤

半徑R 12.5mm

厚度h23mm

質量塊

內徑r17.75mm

外徑r212.50mm

角度φ 60°

厚度h16mm

對于該傳感器的結構，將“扭轉梁兩端面位移為0”設置為邊界條件。 在進行模態有限元仿真分析時不需要施加負載。 向傳感器施加加速度信號后，分析三階振動結果。 一階振動方向指扭轉梁做沿軸向旋轉的運動；二階振動方向指扭轉圓盤整體在豎直方向產生的運動；三階振動方向指扭轉圓盤整體在水平方向產生的運動。 圖3為對應三階分析的結果。

初始結構方案設置下每一階振動方向對應的振動頻率如下：

一階 1 032.2Hz

二階 2 848.4Hz

三階 3 759.2Hz

對初始方案進行靜態有限元仿真分析時，需要在豎直方向先施加一個大小為1g（g=9.8m/s2）的加速度信號，出現的最大位移為9.804×10-5mm，仿真結果如圖4所示。 圖中紅色區域位置表示出現最大位移，深藍色區域位置表示出現最小位移。

通過模態有限元分析可以發現，當施加加速度信號在傳感器上時，傳感器的扭轉梁在二階和三階方向上受到的影響明顯減小。 此外，通過對比發現高階模態諧振頻率是一階模態諧振頻率的兩倍以上，不會影響低階振動信號的產生。

通過靜態有限元分析可以看出，對傳感器結構施加加速度大小為1g的作用后，質量塊位置和扭轉圓盤外圍都產生了顯著的位移變化，最大位移9.804×10-5mm。

2.2 傳感器的增敏設計

由于實際工程可行性的要求，傳感器靈敏度越高越有利于實際運用。 筆者提出如下方案：

a. 方案一，保持其他參數不變，將扭轉梁的半徑減小到1mm，使之變得對加速度做出更敏感的反應，得到的扭應變量相比原來更大；

b. 方案二，保持其他參數不變，把扭轉圓盤的半徑增大到15mm， 使緊貼在扭轉圓盤側面上的光纖光柵纏繞半徑更大，增大了扭轉圓盤上的扭應變，外力作用更加明顯。

兩種增敏方案下所設置的參數見表1。

表1 兩種增敏方案下傳感器的結構參數

對增敏方案一的傳感器進行模態有限元仿真分析和靜態有限元仿真，分析過程如圖5所示，各階振動頻率如下：

一階 689.7Hz

二階 2 130.6Hz

三階 2 733.2Hz

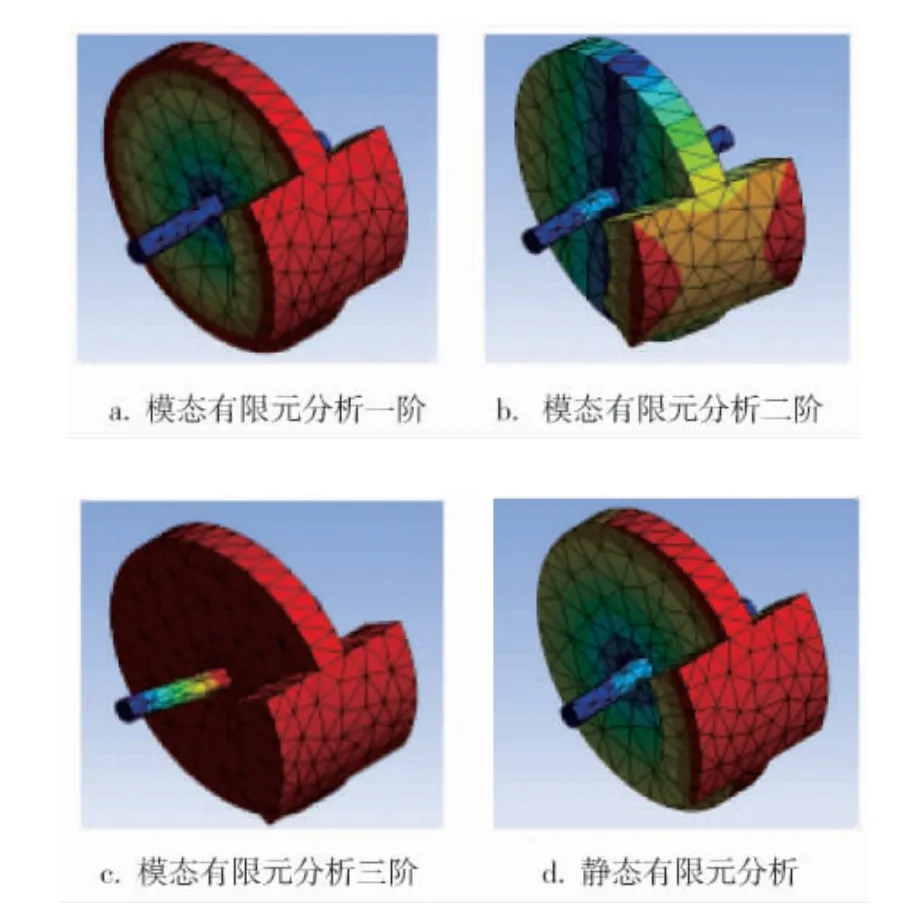
圖5 增敏方案一傳感器結構有限元分析結果

當施加加速度信號在傳感器上時，傳感器的扭轉梁在二階和三階方向上受到的影響明顯減小。 質量塊和扭轉圓盤外圍部分都產生了顯著的位移變化，最大位移為2.137×10-4mm。

對增敏方案二的傳感器進行模態有限元仿真分析和靜態有限元仿真，分析過程如圖6所示，各階振動頻率如下：

一階 1 022.7Hz

二階 2 491.2Hz

三階 3 201.1Hz

圖6 增敏方案二傳感器結構有限元分析結果

該結構的扭轉梁光纖光柵加速度傳感器在1g加速度作用下，質量塊和扭轉圓盤外圍區域均產生最大位移，位移量為1.119×10-4mm。

在增敏方案一中通過改變扭轉梁半徑，傳感器的加速度值有了較大的提高，但傳感器的諧振頻率卻大幅度減小，頻響范圍變窄。

增敏方案二對比初始結構1 032.2Hz的諧振頻率幾乎沒有減小，而且增敏方案二的靜態最大位移為1.119×10-4mm，較初始結構的9.804×10-5mm有了提升，提高了傳感器的靈敏度。

3種方案下的有限元分析結果對比見表2。 可以看出，按照增敏方案二的優化，增大扭轉圓盤半徑，使緊貼在扭轉圓盤側面的光纖光柵纏繞半徑更大，提高了傳感器靈敏度，但同時保證諧振頻率不改變，解決了傳統梁式結構加速度傳感器設計中存在的加速度靈敏度提高會導致諧振頻率降低這一問題。

表2 傳感器的增敏結果對比

2.3 靈敏度計算

根據靜態有限元分析結果，利用最大位移量來計算傳感器的加速度靈敏度。

由于光纖光柵沿傳感器被緊密貼合在扭轉圓盤外圍，扭轉圓盤外圍受到加速度信號影響發生的位移可以轉化為光柵在圓盤切線方向受到的拉力產生的位移。 可計算出光纖光柵所受的應變ε為：

式中 Δx——光柵柵區因受拉變形產生的位移。

傳感器的加速度靈敏度s為［14］：

將初始方案和兩種增敏方案設置的參數代入到傳感器數學模型中，分別計算求出傳感器諧振頻率和靈敏度的理論值、仿真值（表3）。

表3 傳感器理論參數與仿真參數對比

通過對比發現：增敏方案一相對初始結構方案來說，只是減小了扭轉梁的半徑，使扭轉梁變得對加速度信號更敏感， 但從數據中也能發現，無論是仿真值還是理論值，諧振頻率均出現大幅度減小，使傳感器的頻率范圍相比原來更窄。 增敏方案二相對初始方案來說，保持扭轉圓盤質量不改變，增大扭轉圓盤的半徑，這樣使得被繃緊貼合在圓盤側面的光纖光柵半徑變大，從而使扭轉圓盤旋轉時，對光纖光柵帶來的拉力變化更顯著。 增敏方案二諧振頻率的理論值和仿真值與初始方案的相比，雖然有減小但是幅度不大，結構上的改變獲得了靈敏度的提升，效果最優。

3 傳感器的研制及性能參數

為了驗證初始結構和增敏方案的效果，對傳感器進行加工制作。 對應初始結構方案、增敏方案一、增敏方案二的結構，分別制作了3支加速度傳感器，標注為A、B、C，實物如圖7所示。

圖7 傳感器實物

將3支傳感器進行測試，結果見表4。 實際測量的參數與計算值、仿真值存在一定誤差，傳感器的制作過程中已盡可能保證制作工藝和環境條件一致，但仍然存在一定誤差。

表4 傳感器性能參數匯總表

通過對前文提到的3種設計方案進行實物制作和測試后，發現傳感器B相對傳感器A雖然在靈敏度上有了巨大提升，卻以犧牲諧振頻率作為代價，同時與另外兩支傳感器相比，實測值與理論值、仿真值相差較大。 相比較而言，傳感器C與傳感器A的諧振頻率相差不大， 但靈敏度卻有很大提高。 此外，通過對比也發現，傳感器C的線性度、重復性誤差、遲滯性誤差均有所增大，在這些性能指標上不如傳感器A、B。

4 結束語

根據扭轉梁式結構參數，提出了一種光纖光柵加速度傳感器，對傳感器進行了有限元仿真分析、加工制作、性能參數的分析。 研究結果表明，依據增敏方案二所設計的傳感器C與依據初始結構方案所設計的傳感器A相比，諧振頻率保持在1 180Hz左右的同時， 靈敏度有一定提升， 達到6.290pm/g。 與增敏前的結構相比，實測靈敏度相對傳感器A提高了22.97%。 通過改進傳感器的結構，能保證在不降低加速度傳感器諧振頻率的同時提高靈敏度，具有更高的測試帶寬，可實現對高頻信號的檢測。