帝國競爭算法優化板球系統PID參數控制研究

黃文杰 向鳳紅 毛劍琳

（昆明理工大學信息工程與自動化學院）

板球系統具有非線性系統的不確定性，是一類強耦合、欠驅動動力學系統的代表［1］。在這個系統中， 大量的優化方案被應用于小球的定點、軌跡跟蹤等運動。 李愛蓮和吳何琛在圖像處理上的優化方案也被成功應用于其中［2，3］。 PID控制作為一種經典且有效的方法不僅在試驗研究中廣泛應用， 工業生產中的PID控制也很常見。 然而，Roy P等學者發現， 由于板球系統對控制精度的要求較高，且實際控制中具有不確定性，PID控制始終無法在板球系統的控制中保持較好的物理非線性完整度［4，5］。 20世紀70年代以后，智能算法大量問世，遺傳算法（GA）［6］、粒子群算法（PSO）［7］及蟻群算法（ACO）［8］等運算能力較強的控制算法相繼與PID控制法相結合， 大幅度提高了其尋優能力。但是，GA算法在處理較高維數的參數時，易早熟并陷入局部收斂；PSO算法參數較多，在處理關聯性較大的參數能力上顯出不足；ACO算法則有收斂速度慢導致控制時間長的問題［9～11］。 因此，這些算法應用于板球系統這一類欠驅動、強耦合的非線性控制系統時，其效果并不理想。

筆者提出了一種新的可應用于板球系統的基于帝國競爭算法（ICA）的PID控制方法。 選取GBP2001型板球系統作為研究對象， 主要對小球進行定點控制。將試驗數據導入Matlab軟件，與傳統的PID算法和GA-PID算法進行對比， 看出筆者提出的ICA-PID算法在板球定點控制過程中取得了較好的效果。

1 GBP2001型板球系統建模

以固高GBP2001型板球系統（圖1）作為試驗平臺， 以平板的支撐點作為原點建立坐標系，分別在x、y兩個方向對板球系統完成解耦， 得出x方向和y方向的二維分解示意圖如圖2所示。

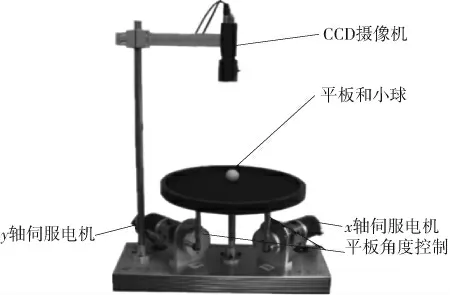
圖1 GBP2001型板球系統

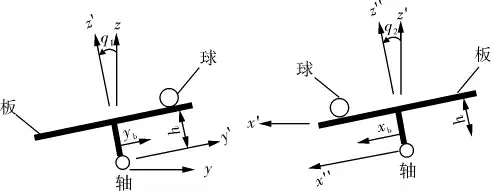
圖2 板球系統二維分解示意圖

板球系統包括小球位置坐標（x，y）、平板轉動角度（q1，q2）等變量，由于板球系統是復雜的非線性系統， 難以獲取其精確的數學模型， 對建模過程中在不影響系統特性的情況下作以下假設：

a. 小球在平板上無滑動和繞小球垂直中心軸旋轉的運動；

b. 忽略小球與平板的角度以及平板面積的影響；

c. 小球在平板上時始終與之保持相接觸的狀態；

d. 建模過程中，將小球和平板之間所有摩擦忽略不計。

建立系統的數學模型對于控制器的設計非常重要，由于板球系統屬于一類復雜的非線性系統，為此筆者從能量的角度建立以拉格朗日法為基礎的數學模型。 板球系統中的各個參數見表1。

表1 板球系統參數表

以平板的幾何中心點為原點建立坐標系，由于在忽略損耗的情況下能量保持守恒，設小球動能為Tb，平板的動能為Tp，則總動能T=Tb+Tp。 對小球和平板分別列出能量方程：

同理， 板球系統總勢能V包括小球勢能Vb與平板勢能Vp，即V=Vb+Vp。 由于在能量分析中取平板為零勢能點，故Vp=0。 小球勢能如下：

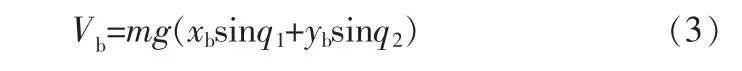
以拉格朗日法建立函數如下：

在實際操作中， 電機轉動位置不受力矩影響，故將式（3）、（4）線性化后可得方程：

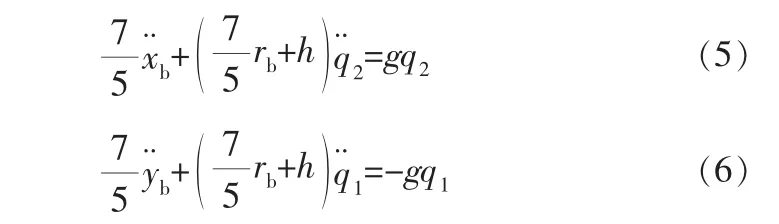
2 板球系統控制器設計

2.1 PID控制器

PID控制器已經廣泛應用在工業生產的過程控制中，它具有安裝簡單、魯棒性強等特點。 PID控制原理如圖3所示。

圖3 PID控制原理

控制算法為：

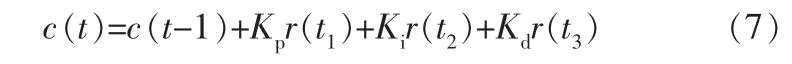
其中，Kp為比例系數，Ki為積分系數，Kd為微分系數；r（t1）、r（t2）、r（t3）是系統的3個輸入量，用控制誤差e（t）來表示：

2.2 板球系統的GA-PID控制器

遺傳算法是借鑒了進化論和遺傳學的一種基于自然選擇和群體遺傳機理的搜索算法［12］。 其算法機理主要包括選擇、 交叉及變異等操作，經過優勝劣汰的過程，種群向最優解不斷進化。 因此， 遺傳算法就是群體不斷淘汰和進化的過程，交叉概率Pc和變異概率Pm的值共同決定了算法的收斂性。 板球系統中應用遺傳算法優化PID參數主要有以下幾個步驟：

a. 隨機產生N個二進制字符串， 取初始種群數量為100、迭代次數為20、交叉概率Pc為0.5、變異概率Pm為0.05；

b. 計算各個體的適應度值以便參數尋優；

c. 應用遺傳算法的復制、交叉和變異算子對群體進行操作；

d. 選擇適應度高的個體，同時淘汰適應度低的個體；

e. 重復步驟c、d， 直至算法收斂或達到終止條件；

f. 最終的Kp、Ki、Kd值表示群體中適應度最好的字符串。

2.3 ICA的應用流程

2.3.1 初始化過程

在ICA中，初始解（country）由向量定義。 筆者研究的問題可以轉化成大小為1×N的向量：

每個國家的成本值用函數f（country）來評估，類似于遺傳算法中的適應度函數：

初始化帝國競爭算法，最初國家的數量定義為Npop， 選擇Nimp作為實力最強的國家建立帝國，其余的Ncol（Ncol=Npop-Nimp）作為帝國殖民地。因此，帝國由帝國主體和一系列殖民地組成。 在最初的帝國集團里， 殖民地數量必須與其能量大小有關， 能量大的帝國擁有的殖民地數量也就越多，反之，則越少。 各個殖民地在帝國主體間按照比例被分配，其分配方法如下：

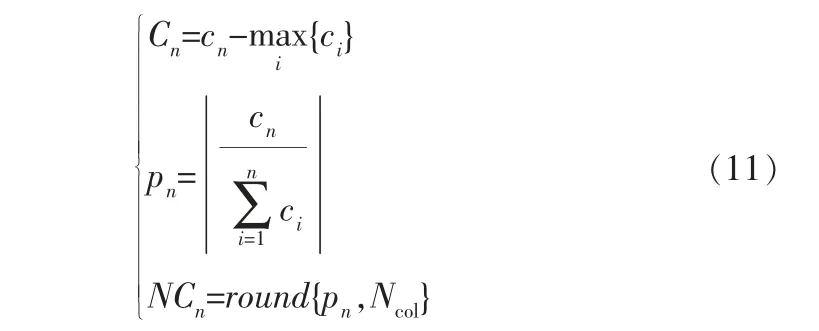
其中cn是第n個帝國的初始成本，減掉帝國中成本最大值后即為相對成本值Cn；pn為第n個帝國初始化分配后的勢力大小；NCn是第n個帝國分配到的殖民地數量。 殖民地在最初分配時依據隨機分配的原則，但勢力強大的帝國會擁有更多的初始殖民地，勢力弱小的帝國會被分配到更少的殖民地數量。

2.3.2 同化過程

在形成了最初的帝國之后，每個帝國的殖民地都開始通過向其相關的方向發展來提高自己的實力。 這個過程的目的是為了使殖民地問題解的結構與帝國所代表解的結構更相似，所以被稱為同化過程（圖4）。

圖4 同化過程示意圖

如圖4所示， 殖民地向帝國方向移動x個單位，其中x是一個隨機變量，服從均勻分布，可表示為：

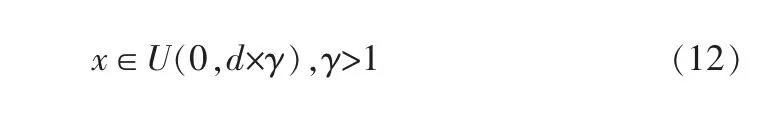
其中，未同化之前帝國與殖民地之間的距離為d；γ是大于1的實數，保證殖民地能從不同的方向靠近帝國。 最初的運動方向本質上不是殖民地和帝國之間的矢量，為了模擬這個事實，將偏差參數θ并入同化過程中有助于提高搜索能力。 θ的恰當選擇對于帝國的集群化和多元化有很大影響，通常θ取π/4能夠很好地達到全局收斂效果［13］。

2.3.3 革命過程

與遺傳算法中的突變過程相似，ICA允許國家的社會政治特征突然出現變化，這個過程被稱為革命。 革命過程的出現能夠防止同化后算法在早期迭代中就收斂到局部最優解。

2.3.4 更新及合并過程

在同化和革命過程之后，一個殖民地可能達到一個比它的成本還低的位置， 如同人類社會中，大多數帝國主義國家會選擇一個具有生存優勢的位置確定都城，這種情況下就需要互換殖民地與帝國的地位：當前帝國變為殖民地，殖民地取代當前帝國。 圖5為帝國更新示意圖。

圖5 帝國更新示意圖

2.3.5 競爭過程

一個帝國集團經過更新、合并等過程之后會具備一定的整體實力，這種整體實力是指主體帝國與所擁有的殖民地的能量的總和。 總成本TCn用帝國初始成本和包含的殖民地成本相加計算：

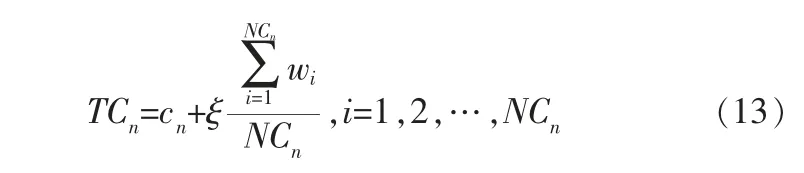
其中，wi為帝國集團的殖民地的代價函數值；ξ是介于0～1之間的非負數，ξ越小，帝國的總成本就越接近帝國國家的成本，反之越小。

帝國競爭算法最重要的步驟之一是構建帝國集團之間的競爭過程。 在這個機制中，最弱國中最弱的殖民地有極大的可能會被較強的帝國搶奪，各個帝國集團在競爭中生存。 最終導致的結果就是強的帝國越來越強， 弱的帝國越來越弱。 為了開始這一過程，首先要對每個帝國的總成本進行標準化，并計算占有概率Pn：

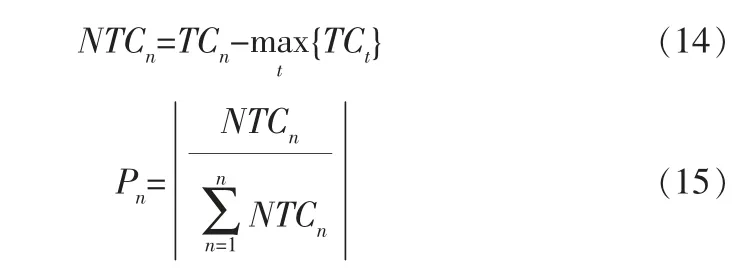
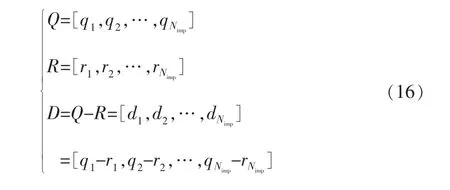
R為與Q大小相同， 參數介于0～1之間的通過均勻分布隨機數組成的向量。由向量Q減去R來計算向量D，D值最大的帝國即可占有自由殖民地。這種帝國獲取殖民地的方式只需極小的計算量，極大地提高了算法的計算效率。 與遺傳算法在交叉操作時選擇母類的輪盤賭過程相似，但該算法因為不需要計算累積分布函數，能夠以更少的迭代次數尋找到全局最優點， 大幅提高了尋優速度，從而減少了板球系統的控制時間。

2.3.6 帝國崩潰與融合過程

在帝國競爭中， 影響力小的帝國會被強大的帝國掠奪從而逐漸失去他們的殖民地， 這導致弱小的帝國隨著時間的推移而崩潰， 最后所有的殖民地都被最強大的帝國占領。 當所有帝國中最強大的一個帝國保存下時算法終止，設置一定的迭代次數， 可選取算法停止時勢利最強的帝國作為輸出的最優解。 將上述算法應用于板球系統PID控制器的整定過程中，并設置跟蹤單位階躍響應曲線的對比試驗驗證算法的優越性。

3 板球系統控制試驗

3.1 板球系統仿真試驗

采用傳統PID、GA-PID和筆者提出的ICA-PID這3種控制方法分別進行試驗， 其中GA-PID控制算法根據文獻［14］的策略，設置種群數量為100、變異概率為0.05、交叉概率為0.5；ICA-PID算法中設總國家數為200、帝國數為8。 3種算法優化同一個數學模型：

PID參數尋優后， 單位階躍響應如圖6所示，參數對比見表2。

圖6 單位階躍響應對比曲線

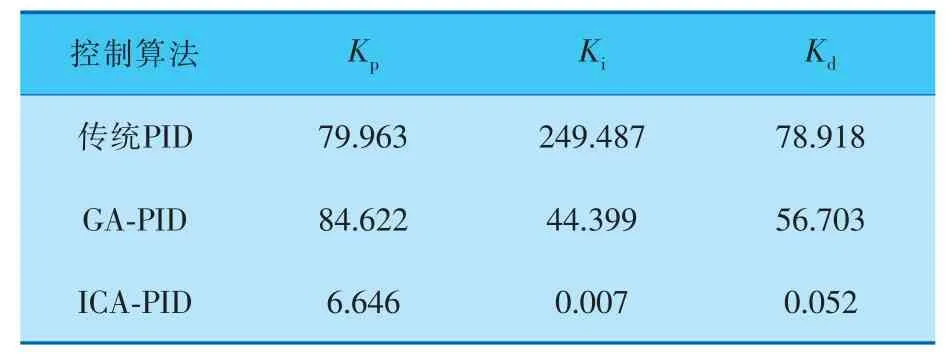
表2 參數對比

綜上可以得出，采用ICA整定的PID階躍響應比傳統PID和GA-PID對控制器的尋優效果好，在板球系統控制試驗中具有調節時間短、收斂速度快和穩態誤差小的優點。

3.2 板球系統軌跡跟蹤試驗

為驗證ICA-PID控制算法的實際可行性，另外設置了基于固高GBP2001型板球系統作為試驗平臺的定點軌跡跟蹤試驗， 開始控制時初始PID參數值設置為Kp=20、Ki=1、Kd=120。 采用上述3種控制算法分別完成小球運動并穩定停止在原點的控制試驗，記錄小球穩定后的試驗數據。

在忽略小球初始位置、光照強度等干擾因素的影響下進行試驗，將最終數據導入到Matlab，以仿真曲線的形式反映小球在x、y兩個方向上的坐標誤差變化和運動軌跡（圖7），具體數據見表3。

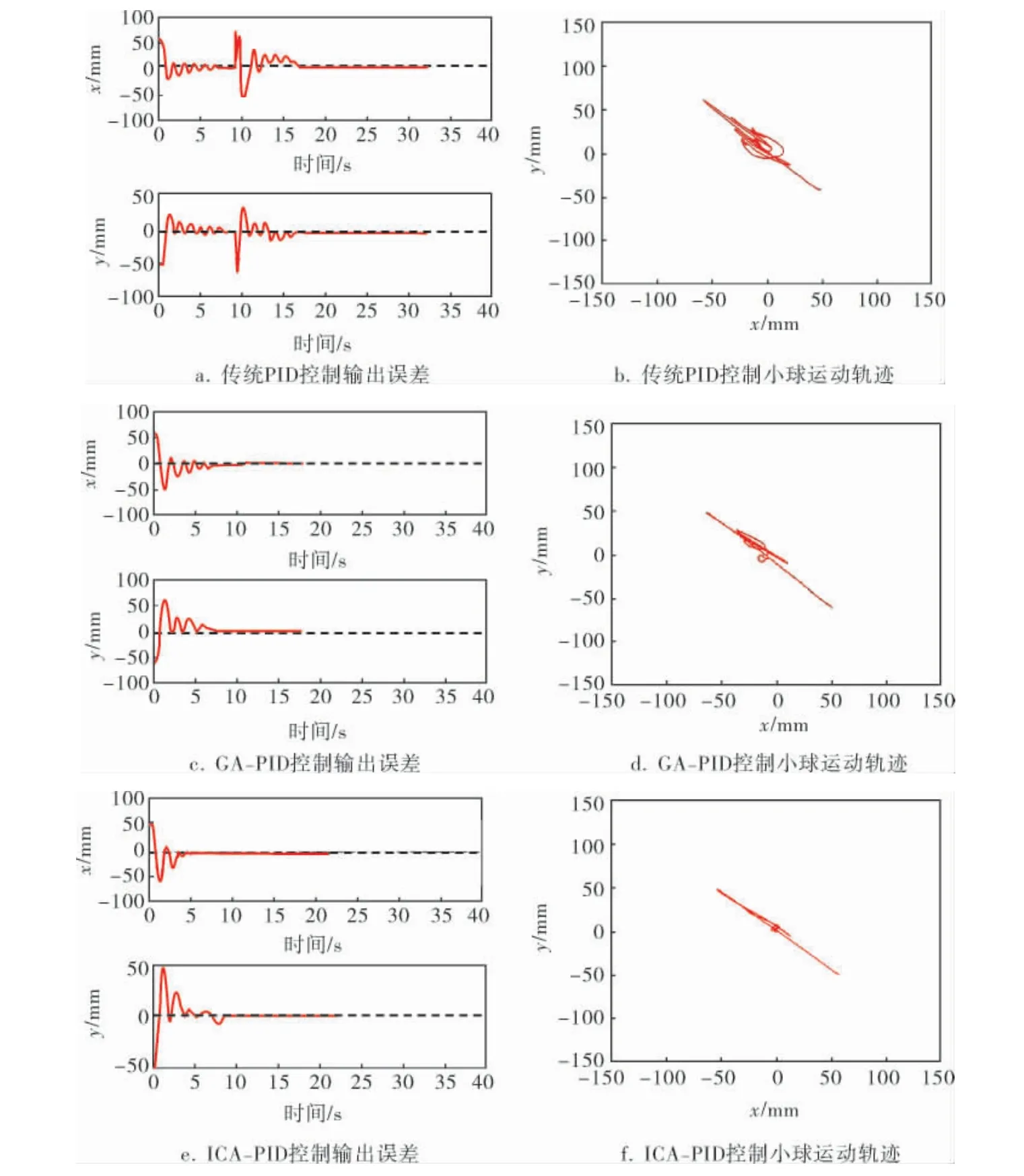
圖7 小球坐標誤差變化和運動軌跡

表3 小球軌跡跟蹤誤差對比

在定點控制試驗中，ICA-PID控制算法的小球軌跡較為簡潔， 穩定后的誤差值相對較小，基本滿足了控制精度的需求。 根據表3，在控制時間方面， 相比于傳統PID控制算法，ICA-PID控制算法能夠大幅度縮短控制時間，減小控制誤差并且優化了PID控制整定參數不良的缺點， 其優化效果相比GA-PID算法在穩定性和縮小超調量方面也具有優勢。

4 結束語

主要研究了GPB2001非線性板球控制系統，提出了ICA-PID算法整定PID控制參數，以實現板球系統控制的優化。 單位階躍響應和小球定點控制仿真試驗，證明了ICA-PID算法在整定PID參數方面具有較強的參數尋優能力，在板球系統中能夠成功應用并且得到不錯的控制效果。