多時滯馬爾科夫跳變系統能量峰值控制方法研究*
(江西理工大學,江西 贛州 341000)
1 引言
馬爾科夫跳變系統是一類特殊的跳變系統,該類系統中各個模態之間的隨機跳變符合一定的統計規律,即系統中各離散有限狀態空間中的不同模態之間的轉移服從馬爾科夫過程。由于隨機馬爾科夫跳變系統能很好地描述一些實際系統,因此自從其被提出后,該類系統的穩定性分析與控制器綜合問題就成為了控制理論研究與應用的熱點之一。本文針對馬爾科夫跳變系統中存在的多時滯現象,基于李雅普洛夫穩定理論研究該類系統的能量峰值穩定性分析與控制器設計方法。得到的相關定理均采用線性矩陣不等式描述,可以方便地通過Matlab線性矩陣不等式工具箱進行求解。
2 模型描述
多時滯馬爾科夫跳變系統的狀態方程描述如下:
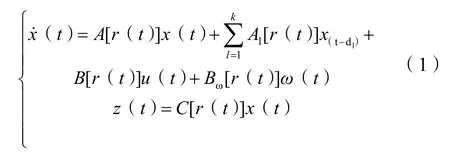
式(1)中:x(t)、u(t)、ω(t)、z(t)分別為系統狀態、控制輸入、外部干擾信號輸入及被控輸出;A[r(t)]、Al[r(t)]、B[r(t)]、Bω[r(t)]及C[r(t)]為適當維數的已知矩陣;dl為系統時滯;r(t)為有限集合r(t)?{1,2,3,…,N}中隨機取值的馬爾科夫隨機過程,跳變轉移矩陣為∏={πij}{i,j∈S}。
轉移概率為:
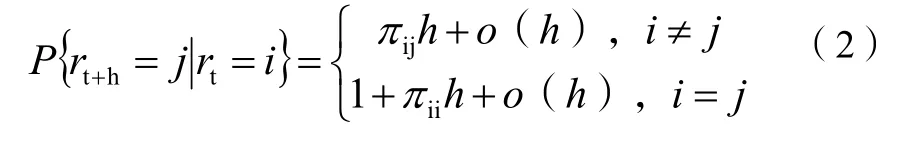
式(2)中:h>0且當j≠i時,表示從時間t的模態i到時間t+h的模態j的狀態轉移概率且有
定義1:對于ω(t)=0均有則馬爾科夫跳變系統被稱為均方漸進穩定。
定義2:如果存在一個常數γ>0使得系統在u(t)=0的情況下均方漸進穩定,且在0初始條件x(t)=0,?t∈[-τ,0]下,對于任意ω(t)∈L2[0,∞),均有則系統為能量峰值穩定。
定義3:如果存在控制器u(t)=K[r(t)]x(t)使得系統閉環狀態下能量峰值穩定,則系統為能量峰值可鎮定。
3 穩定性分析與控制器設計
定理1:對于給定γ>0,如果存在正定對稱矩陣Pi、Q1、U1,非奇異矩陣S,標量βi及γ1i>0使得不等式成立,則系統為能量峰值穩定。

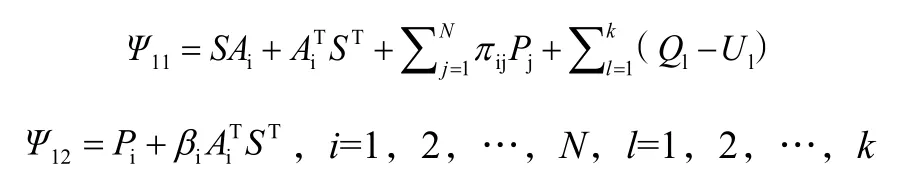
定理2:對于給定γ>0,如果存在正定對稱矩陣非奇異矩陣,標量βi及γ1i>0使得不等式成立,則系統為能量峰值可鎮定。

4 實例
考慮如下雙模態跳變系統,系統包含兩個時滯項,且有d1=0.1,d2=0.2,C1=C2=[0.10.1],B1=B2=[21]T,Bω1=Bω2=
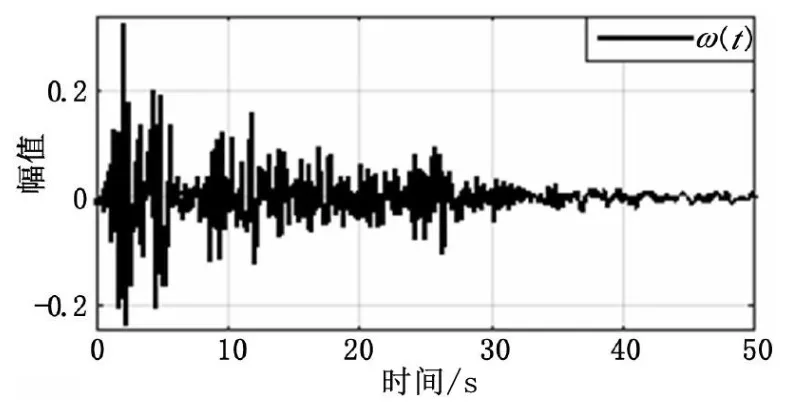
圖1 來自EI Centro1940的地震激勵信號
經計算機仿真可得開環狀態響應曲線如圖2所示。從圖2可知開環狀態下系統是發散的。
基于上文相關參數,現求解定理2可得不等式有解,且得到控制器增益矩陣:K1=[-1.3835-0.9067],K2=[-1.5570-0.7945]
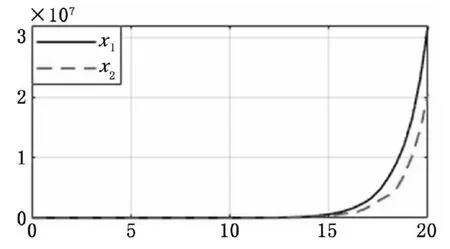
圖2 開環狀態下系統響應曲線
經計算機仿真可得系統在該控制器作用下的狀態響應曲線如圖3所示。從圖3可知系統閉環狀態下是穩定的,且有進而有即閉環系統滿足能量峰值條件。
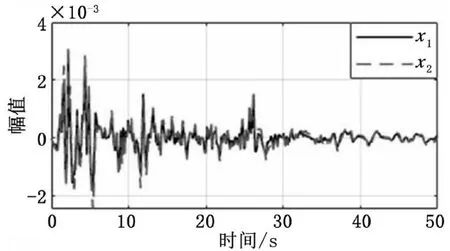
圖3 閉環狀態下系統響應曲線
5 總結
本文基于李雅普洛夫穩定理論及線性矩陣不等式技術研究了多時滯馬爾科夫跳變系統的穩定性分析與控制器設計問題,得到了系統穩定及鎮定控制器存在的充分條件,并通過實例驗證了相關理論的有效性。得到的相關定理均描述成了線性矩陣不等式形式,可以方便地通過Matlab軟件自帶的線性矩陣不等式工具箱進行求解。

