基于包含度的單值中智決策信息系統(tǒng)屬性約簡

陳盼盼，林夢雷

1.閩南師范大學 數(shù)學與統(tǒng)計學院，福建 漳州363000

2.數(shù)字福建氣象大數(shù)據(jù)研究所，福建 漳州363000

1 引言

Pawlak于1982年提出的粗糙集理論[1]是一種用于建模和處理信息系統(tǒng)中不完備和不一致信息的重要數(shù)學工具。粗糙集模型主要是基于等價關系的一對上下近似算子的逼近。然而，在現(xiàn)實生活的許多問題中，由于等價關系要求嚴格，導致粗糙集模型無法應用。因此，文獻[2]通過結合粗糙集和模糊集[3]，提出了粗糙模糊集和模糊粗糙集。同時，對于生活中的決策問題，粗糙模糊集和模糊粗糙集不能同時表示接受、反對和猶豫的程度，文獻[4]將其概念推廣到直覺模糊環(huán)境，提出了直覺模糊集。

作為模糊集和直覺模糊集的推廣，Smarandache提出了中智集[5]的概念。中智集理論是一種新的數(shù)學工具，有助于處理不完全和不確定性問題，一個中智集包含了三個函數(shù)：隸屬函數(shù)、不確定性函數(shù)和非隸屬函數(shù)。這三個函數(shù)的評估程度都是相互獨立的。通過結合中智集理論和粗糙集理論，文獻[6]開創(chuàng)了一種新的混合數(shù)學結構稱為粗糙中智集，并且研究了一些算子和性質。然而，從科學或工程的實際應用角度，粗糙中智集需要重新定義算子。因此，文獻[7]提出了單值中智集，并給出了單值中智集的理論算子和各種性質。單值中智集是一種特殊的中智集，可以方便地用于處理實際問題[8]。由于單值中智集和粗糙集是處理不確定信息的兩種不同的數(shù)學工具，為了同時利用兩者的優(yōu)點，文獻[9]融合了單值中智集和粗糙集提出了單值中智粗糙集模型。粗糙集、中智集、單值中智集和一系列的融合模型在處理不精確信息方面起著重要的作用，并且這些模型都是建立在集合的等價關系、相似關系和廣義二元等關系上，而利用集合的這些關系對實際問題進行決策時過于嚴苛，甚至無法進行合理的決策。因此，文獻[10]利用集合的包含度對集合之間的包含關系進行度量，提出了基于包含度的粗糙集模型。目前一些專家學者也對粗糙集的包含度模型進行了推廣，提出了基于包含度的直覺模糊粗糙集模型[11]。在此基礎上，文獻[12]提出了新的包含度猶豫模糊粗糙集模型。由于單值中智集可以看作是直覺模糊集的推廣，可以方便地處理現(xiàn)實中的不確定性問題和決策問題。但從現(xiàn)有的文獻發(fā)現(xiàn)，已有的單值中智集研究大多集中在直接對單值中智集進行多屬性決策[13-14]，而隨著各種信息技術的快速發(fā)展，這些用于多屬性決策的海量數(shù)據(jù)中存在大量無關以及冗余信息。因此，屬性約簡對于單值中智集的多屬性決策問題更具有實際意義。

2 單值中智集基本概念

定義1[7]設U為非空有限集合，U上的一個單值中智集?是由U→[0,1]的3個有限子集的函數(shù)、和組 成。?可 以 表 示 為或其中:U→[0,1]，:U→[0,1]和:U→[0,1]分別表示A?的真實隸屬函數(shù)、不確定隸屬函數(shù)和虛假隸屬函數(shù)，并滿足

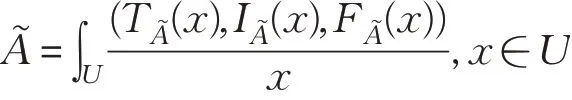
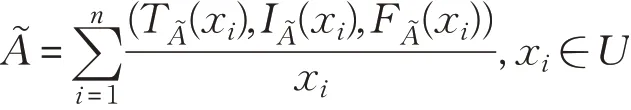
定義2[7]對任意的A?,B?∈SVNS(U)，有如下定義：

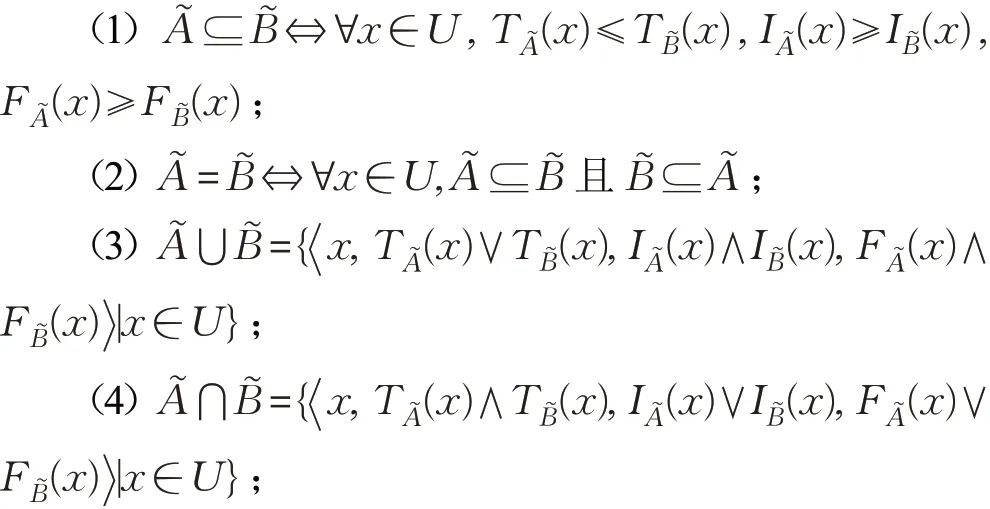
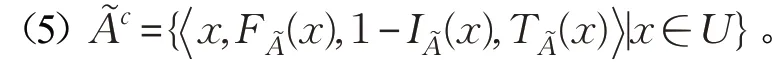
其中，“∨”和“∧”表示取最大和最小。

定理1[15]對任意的，有如下性質：

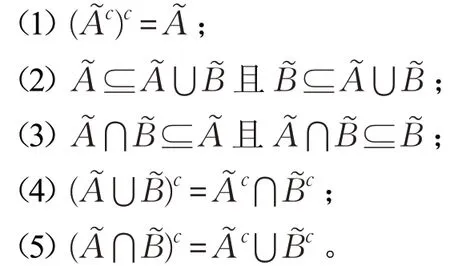
定義3[15]設U為非空有限集合，U上的一個單值中智關系定義為：

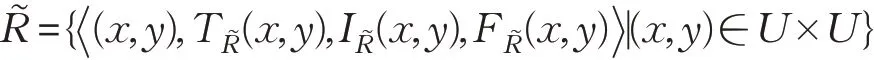
假設U={x1,x2,…,xn}，一個單值中智關系可以表示為矩陣，其中，矩陣中數(shù)對(i,j)位置表示xi和xj之間的單值中智數(shù)。

若單值中智關系R?滿足以下條件則稱為單值中智相似關系：

3 基于包含度的單值中智決策信息系統(tǒng)屬性約簡

3.1 單值中智決策信息系統(tǒng)

定義4設U為非空有限集合，A={a1,a2,…,al}為條件屬性集，表示分別由屬性a1,a2,…,al誘導的單值中智相似關系，則S=(U,A)稱為單值中智信息系統(tǒng)。若d為決策屬性，則S=(U,A?d)稱為單值中智決策信息系統(tǒng)。

假設論域U被決策屬性d劃分為U/d={d1,d2,…,dr}，故劃分的決策類可表示為：

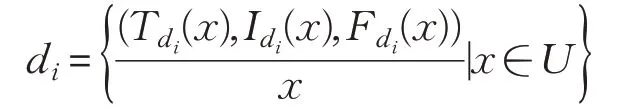
其中

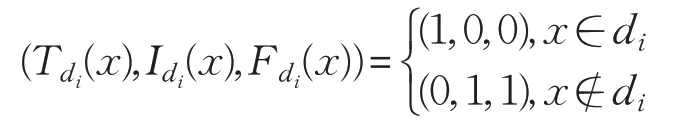
定義5給定S=(U,A?d),U/d={d1,d2,…,dr},表示由條件屬性集A誘導的單值中智關系，?x∈U，x的單值中智決策定義為：

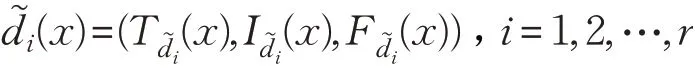
其中

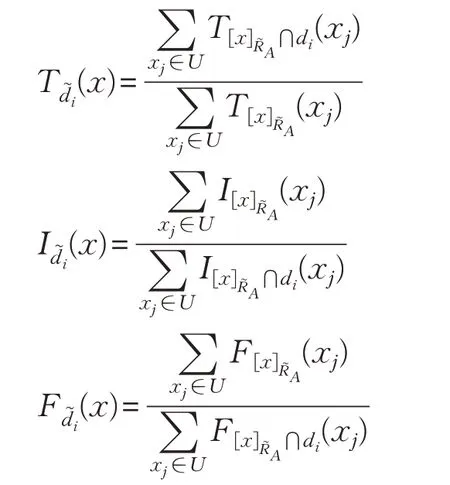
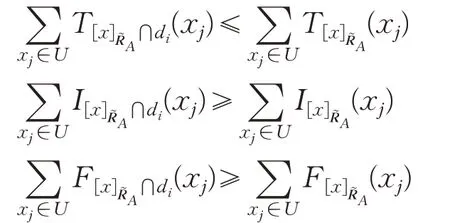
例1設論域U={x1,x2,x3,x4,x5}，條件屬性集A={a1,a2,a3}，論域U被劃分為U/d={d1,d2,d3}，其中d1={x1,x2}，d2={x3,x4}，d3={x5}，A誘導的單值中智關系為：

由已知有：

每個對象的單值中智相似類為：

由定義2的（4）可知：

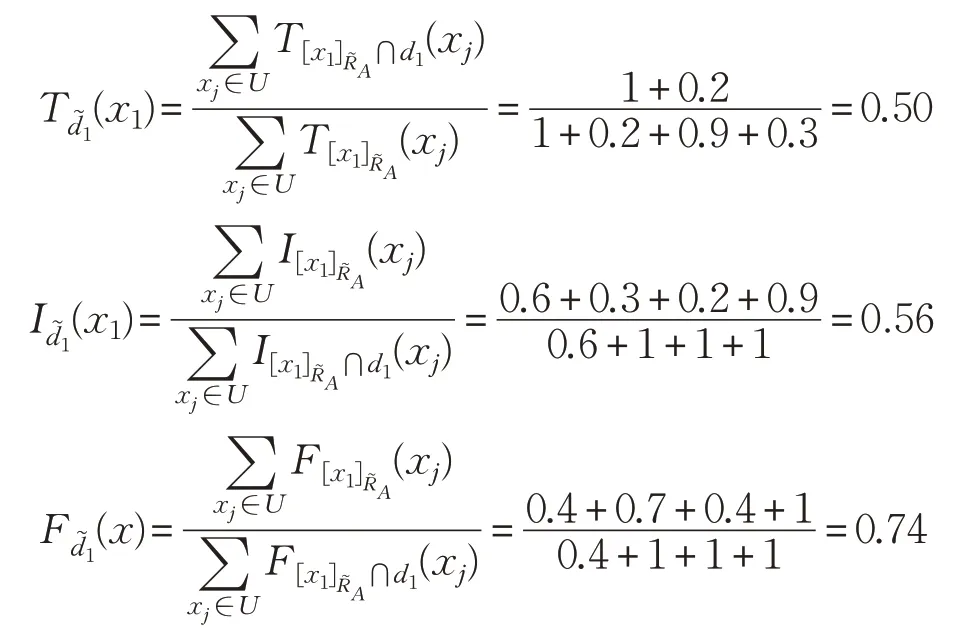
同理可求得：

因此

同樣可求得：

在應用粗糙集和模糊集理論處理生活中的實際問題時，往往用到集合的包含關系，而由于集合之間的包含關系過于苛刻，通常用集合包含度來度量。集合的包含度是集合包含關系的一種推廣，是不確定理論中的一種重要度量工具。同樣，單值中智集在處理生活中的決策問題時，利用單值中智包含度更有利于實際問題的解決。

3.2 單值中智包含度

定義6對于任意的A?,B?,C?∈SVNS(U)，若映射D:SVNS(U)×SVNS(U)→[0,1]滿足：

則稱D為SVNS(U)上的包含度。

基于以上包含度的公理化定義，本文給出單值中智集包含度的兩個計算公式，具體形式為：

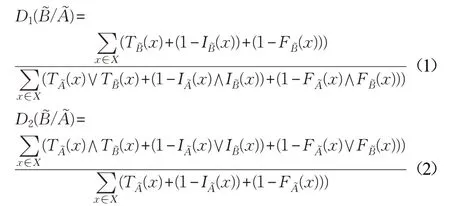
定理3公式（1）、（2）都是SVNS(U)上的包含度。

證明 以式（1）為例證明。

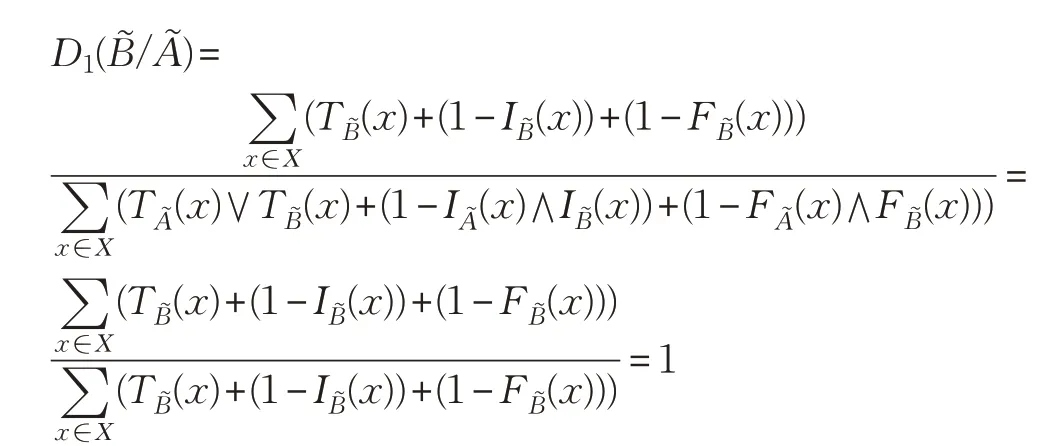
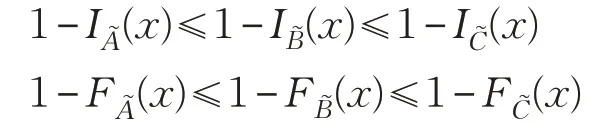
故

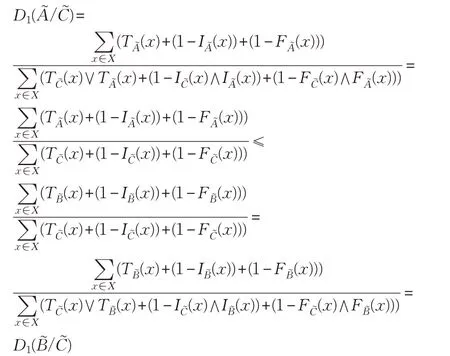
綜上（1）～（3）可知，式（1）為SVNS(U)上的包含度。類似地，可以證明式（2）為SVNS(U)上的包含度。

接下來的證明和計算，均以式（1）為例進行，若采用式（2）則完全類似。

3.3 基于包含度的單值中智粗糙集模型及其性質

定義7對于單值中智決策信息系統(tǒng)S=(U,A?d)條件屬性集A={a1,a2,…,al},U/d={d1,d2,…,dr}，單值中智相似關系，D為SVNS(U)上的包含度，則決策d關于B的近似空間定義為：

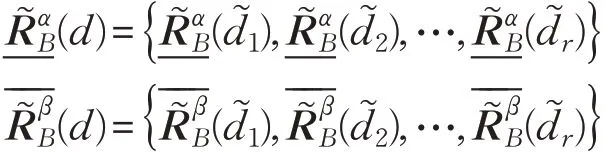
其中：

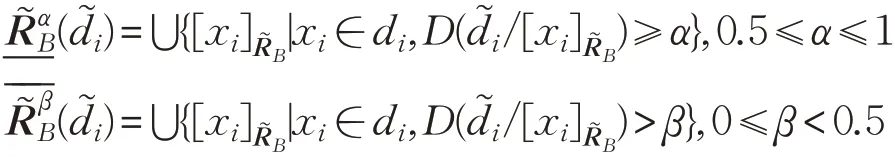
決策系統(tǒng)的正域定義為：

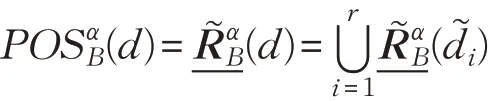
決策系統(tǒng)的邊界定義為：

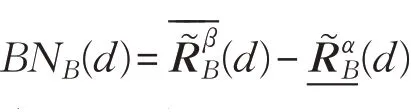
定理4設0.5≤α≤1，0≤β＜0.5，D為SVNS(U)上的包含度，則包含度近似算子滿足下列性質：

證明（1）對于任意α,β和決策類di∈U/d，由定義7可知顯然成立。

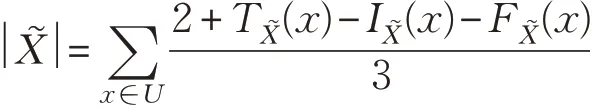
定理5對于任意的A?,B?∈SVNS(U)，有：

（3）同理（2）可證。

定義9給定單值中智決策信息系統(tǒng)S=(U,A?d),決策屬性d對條件屬性B?A的依賴度為：

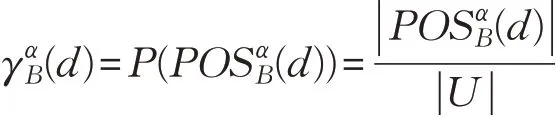
定理6給定單值中智決策信息系統(tǒng)S=(U,A?d),和包含度閾值α,B1,B2?A，如果，則：

定義10給定單值中智決策信息系統(tǒng)S=(U,A?d),B?A，稱B為該單值中智決策信息系統(tǒng)的約簡，如果B滿足：

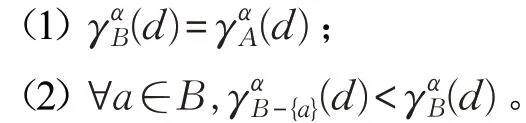
定義11給定單值中智決策信息系統(tǒng)S=(U,A?d),B?A且a∈A-B，單值中智屬性a相對于條件屬性集B的重要度定義為：

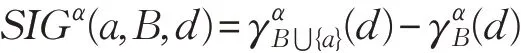
3.4 案例分析

根據(jù)定義11重要度的定義，下面給出基于單值中智正域的屬性約簡算法。該算法采用前向貪心搜索策略，以空集為起點，依次選擇屬性重要度最大的屬性加入約簡集中，直到增加任何屬性，屬性的依賴度不再增大為止。

算法1基于單值中智正域的屬性約簡算法

輸入：S=(U,A?d)；

輸出：約簡B。

（1）初始化B=?

（2）對任意ai∈A-B

計算SIGα(ai,B,d)=(d)-(d)

（3）選擇屬性ak，使其滿足

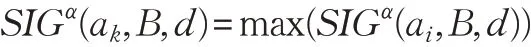
（4）if SIGα(ak,B,d)＞0

B?{ak}→B

返回第（2）步

else

返回B

end

根據(jù)以上算法，給出下面相應的實例進行計算單值中智決策信息系統(tǒng)的約簡。

例2給定單值中智決策信息系統(tǒng)S=(U,A?d)，U={x1,x2,x3}，A={a1,a2,a3}，屬性集誘導的單值中智相似關系分別為R?a1,R?a2,R?a3，令α=0.7，且

決策屬性d將論域劃分為U/d={d1,d2},其中d1={x1,x2},d2={x3}，即決策為{?}。由定義4有：

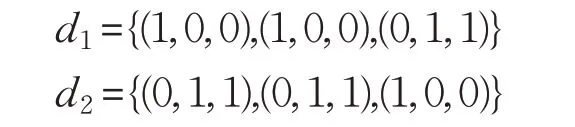
（1）根據(jù)算法1首先令B=?，分別計算單值中智屬性a1,a2,a3的重要度，對于屬性a1有：

由以上定義可得：

利用例1方法有：

根據(jù)包含度計算公式（1）可得：

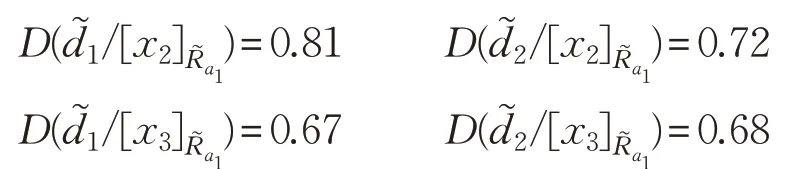
由于x1,x2∈d1,x3∈d2,且，故：

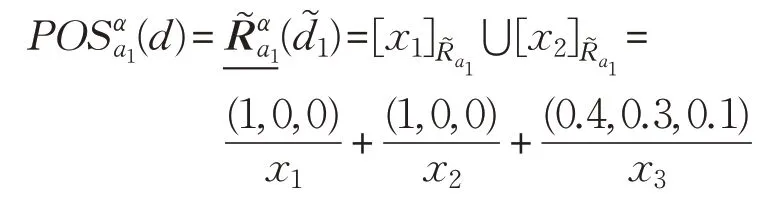
結合定義8和定義9得：

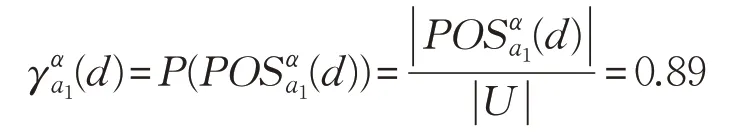
由此，SIGα(a1,B,d)=0.89。

對于屬性a2有：

同理單值中智屬性a1下的計算，可得：

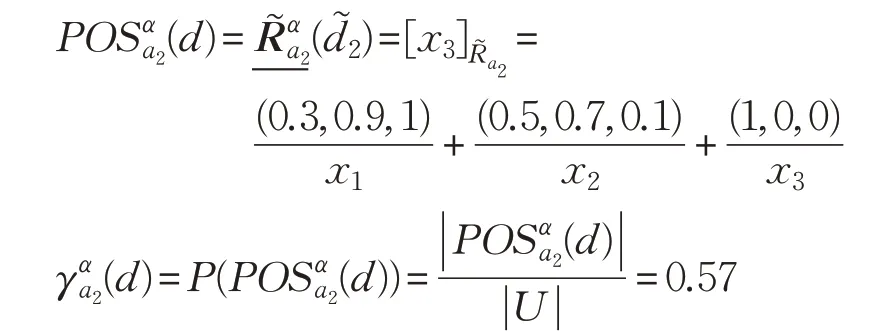
故SIGα(a2,B,d)=0.57。

對于屬性a3有：

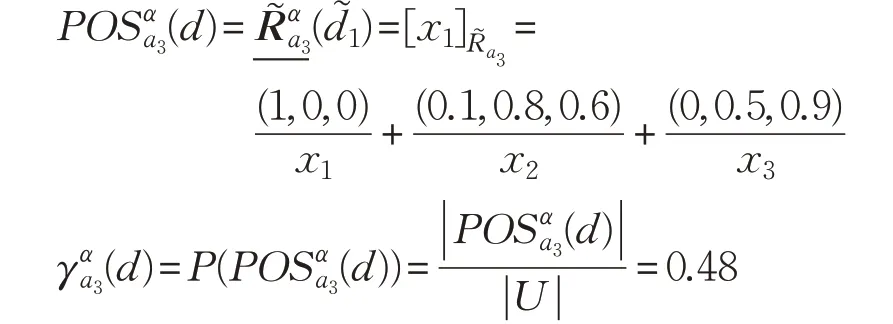
故SIGα(a3,B,d)=0.48。

（2）根據(jù)算法1的步驟（3），選擇單值中智屬性重要度最大的a1，令B=a1，A={a2,a3}，SIGα(a1,B,d)＞0。

同（1）可得：

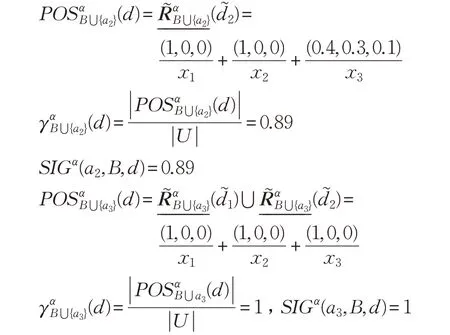
故SIGα(a3,B,d)=1-0.89=0.11,SIGα(a2,B,d)=0,因此，B={a1,a3},A={a2},由于SIGα(a2,B,d)=0,SIGα(a3,B,d)＞0。故該單值中智決策信息系統(tǒng)的約簡為B={a1,a3}。

4 結束語

本文利用單值中智集可以同時描述真實、猶豫和非真實三方面不確定性信息的特點及集合之間的包含程度對不確定信息的度量，給出了單值中智集的包含度定義，并融合單值中智集的包含度和粗糙集進行建模，提出了基于包含度的單值中智粗糙集模型。該模型加入了變精度參數(shù)，使得在處理不確定性問題時能做出更合理的決策，同時降低問題的不確定性。最后，利用該模型對提出的單值中智決策信息系統(tǒng)進行屬性約簡。本文所提模型在處理不確定性問題方面的適用范圍更強，應用領域更廣泛。