機場出租車司機決策問題研究

魏逸凡 東北電力大學理學院

1 .引言

近年來，隨著我國經濟水平的不斷提高，全社會運輸需求增加，航空運輸作為現代交通體系中較為快捷的運輸方式，受到了廣泛歡迎。機場作為航空運輸的基礎，具有壟斷性、稀缺性的特點，在我國得到了極大發展。隨著我國機場數量的增多和航空運輸需求的擴大，我國機場業務量保持著快速穩步增長態勢，旅客吞吐量增速超過10%，貨郵吞吐量保持穩步提高。

2 .模型建立與求解

2.1 模型的建立

2.2.1 出租車司機決策因素機理分析

在乘客下機后要去周邊的目的地，出租車是主要的交通工具之一。送客到機場的出租車司機會在已知某時間段抵達的航班數量和“蓄車池”已有的車輛數的情況下做出決策。以下為兩種決策方案：

（A）前往“蓄車池”等待載客返回市區，依據先來后到排隊入場載客。

（B）直接返回市區拉客。

一般情況下，收益會成影響出租車司機決策的主要因素，司機會權衡方案A 與方案B 的收益與損失。選擇方案A可以收獲載客收益z，但是司機由于前往“蓄車池”等待，所以會付出隱形損失：時間成本k；而方案B 可以收獲回市區后的接客收益，此收益為潛在載客收益s，但是由于回市區未拉到客人，所以會付出一定的空載費用l。

以下為出租車司機決策相關因素影響機理思維導圖：

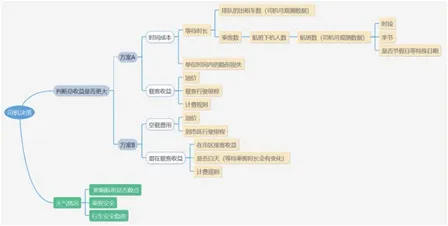
圖1 出租車司機決策相關因素影響機理思維導圖

2.2.2 方案A 的總體收益模型

(1）方案A 的基礎模型

如果司機選擇方案A，那么司機的總體收益QA為：QA=z-k（1）

其中，z 為載客收益，k 為時間成本。

(2）方案A 的總體收益

載客收益z 與當地的油價、載客行駛里程u 與當地的出租車計費規則有關，當地的油價與當地的出租車計費規則為定值。假設載客行駛里程u 服從范圍為[r1-r2，r1+r2]的泊松分布，其中r1為市中心到機場的距離，r2為城市半徑。

由以上模型知，方案A 的總體收益為：

2.2.3 方案B 的總體收益模型

(1）方案B 的基礎收益模型

如果司機選擇方案B，那么司機的總體收益QB為：

QB=s-l （3）

其中，s 為潛在載客收益，l 為空載費用。

(2）空載費用與潛在收益模型

空載費用l 由油價與司機空載到市區的行駛里程決定。油價為當地出租車的平均油價。這里假設司機空載到市區的行駛里程與到市區載客行駛里程u 獨立同分布，均服從范圍在[r1-r2，r1+r2]的泊松分布。其中r1為市中心到機場的距離，r2為城市半徑。

潛在載客收益s 為在出租車司機在空載返回之后進行載客，從而形成潛在的載客收益。潛在載客收益s 與在市區的載客收益z'與在市區等待載客時長tj有關。在市區的載客收益z'與當地的油價、市區載客行駛里程u'與當地的出租車計費規則有關。當地的油價與出租車計費規則均為定值。假設市區載客行駛里程u'服從范圍為[3， 2*r2]的泊松分布，即假設乘客均在城市范圍內活動且最小行駛里程為3 km。

2.3 模型的求解

2.3.1 出租車司機選擇決策模型

出租車司機選擇A 方案與B 方案的主要因素是收益，天氣也是出租車司機進行選擇的因素之一。但是由于天氣因素多變，且如下雨、下雪等天氣由于程度不同，影響判斷的參數難以一一量化，所以本文假設模型的前提為不會遇到對司機決策影響過大的天氣，如果遇到司機會直接選擇B 方案或直接回家。

出租車司機選擇A、B 方案收益之差Z 為：

Z= QA-QB（4）

將方案A的總體收益模型與方案B的總體收益模型帶入式（4），即有：

其中，z 為載客收益，l 為空載費用，s 為潛在載客收益，b 為“蓄車池”車量數，f 為單位時間內的隱形損失，M 為當前時段的客機平均最大容量，N 為當前時段客機的數量，θ為客座利用率，β為可決系數。

決策Dec 為：

A 即為選擇A 方案，B 即為選擇B 方案。當Z=0 時，考慮到在停車場等待司機會付出較少的精力，所以將其劃入A 方案中。

2.3.2 司機選擇策略方案

由出租車司機的選擇決策模型中可以看出，載客收益z 與空載費用l 由油價與司機的行駛里程決定。出租車司機在選擇A 方案時，會出現載客收益z，我們假設了司機載客行駛里程u 服從范圍在[r1-r2，r1+r2]的泊松分布，所以為有區間的隨機值。司機在選擇B 方案時，會出現空載費用l，司機空載到市區的行駛里程與到市區載客行駛里程u 獨立同分布，均服從范圍在[r1-r2，r1+r2]的泊松分布，所以也為有區間的隨機值。

總體收益模型的最后一項參數有：“蓄車池”車量數b、單位時間內的隱形損失f、當前時段的客機平均最大容量M、當前時段客機的數量N、客座利用率θ、可決系數β。最終司機的選擇策略為：首先根據自己的經驗判斷出可決系數的大小，然后觀察“蓄車池”車量數與當前時段客機的數量，最后將相應數值代入出租車司機選擇決策模型即可判斷出A 方案還是B 方案為最優方案。