直升機地面共振影響參數優化設計

馬小艷，陳 浩

(中國直升機設計研究所，江西 景德鎮 333001)

0 引言

直升機地面共振是一種旋翼和機體耦合的動不穩定性問題，是自激振動。主要的自激振源是旋翼后退型擺振運動與旋翼槳轂中心有水平運動的機體模態的耦合。地面共振是直升機在地面開車或滑行、滑跑時發生的。地面共振的發散程度極大，往往在幾秒鐘內就會導致機體及旋翼的破壞[1]。

直升機在地面工作狀態能夠產生地面共振的內因是它存在兩個機械振動系統，且這兩個系統振動特性之間有特定關系。這兩個振動系統是：由各旋轉槳葉繞垂直鉸擺振組成的旋翼振動系統和機體在起落架上組成的機體振動系統。直升機發生地面共振的外因是直升機收到足夠大的外界初始擾動。如果槳葉減擺器和起落架緩沖支柱的阻尼足夠大，或者旋翼系統產生的離心激振力的頻率和全機在起落架上的振動頻率相差足夠遠，那么這兩個系統因外界干擾而激起的振動就會彼此削弱，直至消失，就不會發生地面共振。因此，設計直升機的過程中必須合理選擇旋翼系統和起落架性能參數，以保證直升機在規定的使用條件下不具備發生地面共振的內因條件[2-4]。

直升機地面共振問題是一種危及直升機安全的自激振動問題，其動不穩定分析是直升機型號設計中的一項重要工作[5]。本文以典型直升機為例，通過專門的地面共振分析計算方法[6-8]，對影響地面共振的旋翼系統和起落架參數進行合理優化設計，形成該型機地面共振設計要求分析的思路，在型號的方案設計或詳細設計階段具有重要的設計指導價值。

1 計算方法

直升機地面共振問題，本質上就是帶有彈性支座的旋翼在旋轉平面里的動不穩定性問題。分析計算直升機地面共振采用“空間模型”，分別考慮機體系統和旋翼系統，并作下列假設：

1)在旋翼旋轉平面內，只考慮槳葉繞垂直鉸的擺振運動,不考慮槳葉的揮舞運動和扭轉運動。

2)機身和槳葉都是剛體，不考慮其彈性變形。因為它們的彈性變形與起落架的位移和槳葉繞垂直鉸的擺振位移相比是很小的。槳葉和槳轂用垂直鉸連結。

3)不考慮空氣動力作用。

4) 起落架和減擺器的剛度、阻尼特性都假定為線性的。

機身作為剛體，在空間共有六個自由度：x，y，z，φ，θ，β，定義如下：

x描述機體在X軸方向的平動自由度，方向同X軸；

y描述機體在Y軸方向的平動自由度，方向同Y軸；

z描述機體在Z軸方向的平動自由度，方向同Z軸；

φ描述機體繞Y軸的轉動自由度，方向按左手定則；

θ描述機體繞X軸的轉動自由度，方向按左手定則；

β描述機體繞Z軸的轉動自由度，方向按右手定則。

圖1 機體系統模型

對于每一片槳葉，只考慮槳葉繞垂直鉸擺振這一個自由度，用ξi表示。因此，旋翼系統實質上只是旋轉平面動力系統。

圖2 旋翼系統模型

經過多槳葉坐標變換以后，旋翼旋轉平面動力系統可用兩個自由度η、ζ來表示：

綜合上述分析，整個動力系統計算模型共考慮八個自由度。

對應機身六個自由度的廣義力平衡方程見公式(1)-(6)，對應廣義坐標的旋翼運動方程見公式(7)-(8)，具體推導過程見文獻[2]。

(1)

KZNxN-(2KZMzM+KZNzN)sinα]z+

(2)

(3)

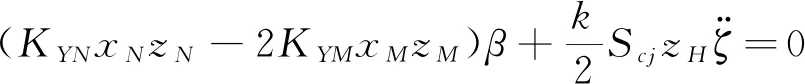
(4)

(5)

(6)

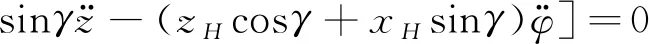
(7)

(8)

直升機地面共振計算采用特征值計算方法[9-10]。將運動方程(1)-(8)簡寫成下列形式：

(9)

式中，{X}={x,φ,y,θ,z,β,η,ζ}T為8個元素的向量，[M]、[C]、[K]為系數矩陣。

在運動方程(9)中，令：

則得狀態方程：

(10)

式中，

為16個元素的向量，

在某一旋翼轉速Ω下，先計算系數矩陣[M]、[K]、[C]；再按上式形成[A]、[B]矩陣；然后，選用任一解特征值的標準程序求方程(9)的特征值σi±jωi(i=1,2, ……,8)，特征值的實部σi表示系統的阻尼，虛部ωi表示系統的頻率。

根據旋翼擺振后退模態的特征值實部判別系統的穩定性：若特征值實部小于0，則在該旋翼轉速下系統是穩定的，若特征值實部大于0，則系統不穩定。如此，取不同的Ω，可在(Ω，σ)平面上得到一條連續曲線，即“地面共振”阻尼曲線。根據該曲線的正負，就可以確定“地面共振”不穩定區域或臨界穩定轉速。同樣，根據旋翼擺振后退模態的特征值虛部，在(Ω，ω)平面上得到一條連續曲線，即“地面共振”頻率曲線。

在地面共振計算中，轉速穩定裕度η=nc/Ω0-1，Ω0為旋翼可能達到的最大轉速，nc對應不穩定區下邊界的轉速。

2 優化設計

要使直升機不發生地面共振，一般設計上要考慮兩個方面：頻率設計和阻尼設計。頻率設計要求旋翼擺振后退型模態頻率與機體在起落架上的各階固有頻率避開得足夠遠，這是防止直升機發生地面共振首先應滿足的要求；阻尼設計要求旋翼-機體系統提供的可用阻尼應大于該動力系統為維持臨界穩定狀態所需的阻尼，并有一定阻尼儲備量。

以典型直升機最大起飛重量裝載狀態為例，進行地面共振影響參數優化設計。由該型直升機地面共振計算結果可知，影響其地面共振特性的主要是機體側向二階模態。

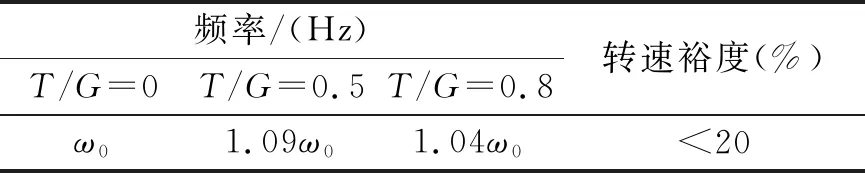
表1 二階模態頻率對比

2.1 頻率設計

頻率設計要求主要是為了保證在旋翼額定轉速外有足夠的轉速裕度。在直升機方案設計階段，一般要求該轉速裕度不小于20%。基于此要求，需要對側向二階模態進行調頻率，即將側向二階頻率ω0調到1.41ω0，見圖3。

圖3 頻率匹配圖

在起落架其他條件不變的情況下，影響機體側向二階頻率的因素主要是機輪側向剛度。表2給出了機輪側向剛度對側向二階模態頻率的影響。

由表2可知，若要滿足有不低于20%的轉速裕度，機輪側向剛度系數取2.0，即需將機輪側向剛度提高到原來的2倍以上。

表2 機輪側向剛度對側向二階模態頻率的影響

實際上，受搖臂和緩沖支柱側向剛度以及機輪與地面摩擦力影響，很難保證機輪側向剛度有如此大幅的提高。故為保證大重量時有足夠的轉速裕度，可考慮調整旋翼擺振后退型模態頻率ωξ。表3提出了不同機輪側向剛度時對粘彈(或液彈)減擺器剛度系數的要求。

表3 粘彈(或液彈)減擺器剛度系數要求

若旋翼采用粘彈(或液彈)減擺器，能夠保證在整個減擺器擺振幅值范圍內有20%的轉速裕度。

2.2 阻尼設計

阻尼設計需要保證旋翼-機體動力系統有足夠的阻尼抑制地面共振發生。基于此原則，開展地面共振特性對減擺器阻尼、起落架阻尼的敏感性分析，對相關影響參數優化設計，見圖4。

圖4 影響參數分析結果

3 綜合驗證

基于綜合分析，考慮減擺器阻尼增加20%，緩沖支柱剛度減少50%，機輪側向阻尼增加20%，分別計算表4中的三種工況。地面共振阻尼曲線見圖5。

表4 旋翼、起落架參數對地面共振特性的綜合影響

備注：a為減擺器阻尼，b為緩沖支柱剛度，c為機輪側向阻尼。

圖5 地面共振阻尼曲線

由表4和圖5可知，綜合優化旋翼、起落架參數后，取減擺器阻尼系數1.2，緩沖支柱剛度系數0.5，機輪側向阻尼系數1.2，在不同升力比狀態，該型直升機不存在不穩定區，且轉速裕度均大于20%。

4 結論

通過對典型直升機地面共振影響參數優化設計，可得到如下結論：

地面共振設計應首先考慮頻率設置要求，保證在減擺器整個擺振幅值范圍內均有足夠的轉速裕度，可通過優化機輪側向剛度調整機體在起落架上的頻率來實現該目標。

在保證方案可行性的情況下，為盡可能增大系統的穩定性，需綜合協調考慮旋翼減擺器、緩沖支柱以及機輪的剛度和阻尼。

本文提及的地面共振影響參數優化設計思路通俗易懂，考慮因素全面，能夠為直升機型號在方案設計或詳細設計階段提供設計指導，具有重要的應用價值。