基于數字補償器的比例調速閥特性仿真

趙海娟， 張寶成， 黃家海， 王 鶴, 束世辰

(1.太原理工大學機械與運載工程學院， 山西太原 030024； 2.太重集團榆次液壓工業有限公司， 山西榆次 030600; 3.北自所(北京)科技發展有限公司, 北京 100120)

引言

比例調速閥作為液壓系統重要的控制元件，廣泛應用于液壓執行元件的流量控制，在變負載工況下，為保證執行機構的平穩運行，比例調速閥需要較高的穩定性。傳統的壓差補償型[1-2]比例調速節流閥在閥口串聯或并聯機械式壓力補償器，維持節流閥兩端壓差近似恒定，但其控制精度低、頻響低。為了改善這一技術難題，王慶豐等[3]、MULLER等[4]提出了一種數字流量補償技術，該技術采用壓力傳感器檢測閥進出口壓力，并將壓力信號輸入數字流量補償器實現對流量的精確控制。HUANG等[5]提出一種帶先導數字補償器的兩級比例調速閥。根據半經驗流量計算公式的近似表達式計算補償電壓，改變先導閥閥芯開口補償閥口壓差變化引起的流量變化。王灝等[6]提出以雙線性插值法為工作原理的流量補償控制器，根據主閥閥口壓差精確推算出先導閥的補償電壓，控制主閥流量恒定不變。近年來國內外學者還采用了不同的控制方法提高比例系統控制性能。LI Rong等[7]在電液比例控制系統中采用基于MATLAB的PID校正技術，使小慣性系統在負載變化率較低時，擁有更好的時域與頻域性能指標。談懷江等[8]在大流量比例閥開度控制中，利用模糊控制在線動態調整PID控制參數。付永領等[9]采用滑模變結構控制策略控制機電控制器,設計了雙滑模變結構控制器，提高了系統的頻響和控制精度。以上研究表明： 控制算法提高了系統的控制精度與穩定性，在當前控制算法下，比例調速閥具有較高的靜態特性與等流量特性。但當系統存在瞬時負載干擾，輸出流量會出現較大的流量超調現象，嚴重影響比例調速閥的動態性能。

本研究選擇具有流量放大原理的二級比例流量閥(Valvistor閥)[10-12]作為研究對象，鑒于當前采用的補償方法無法改善由于負載階躍引起的流量超調問題，采用壓差前饋控制[13]與廣義預測控制結合的控制策略解決上述問題。廣義預測控制[14-16](Generalized Predictive Control,GPC)以受控自回歸積分滑動平均模型(CARIMA)為預測模型，利用系統輸入輸出與期望數據預測未來時刻輸出數據，通過優化成本函數，得到最優控制增量，加快閥芯響應速度，精確控制Valvistor閥的輸出流量；主閥口壓差通過壓力傳感器反饋到數字補償器中，經壓差前饋控制器計算得出控制電壓，與廣義預測控制最優控制增量共同作用于先導閥。

1 工作原理

圖1為新型比例調速閥工作原理。新型比例調速閥由流量放大型Valvistor閥、先導比例節流閥、壓力傳感器、數字補償器組成。主閥下腔由閥芯表面的反饋窄槽與控制腔連接，控制腔與先導閥進口連接，行成流量-位移反饋。根據流量反饋原理，先導閥控制電壓變化時，先導閥流量qp變化，導致主閥控制腔壓力pc變化，主閥芯位移改變，當主閥流量qm是先導閥流量qp的線性放大時，主閥閥芯停止運動，流量達到穩定。

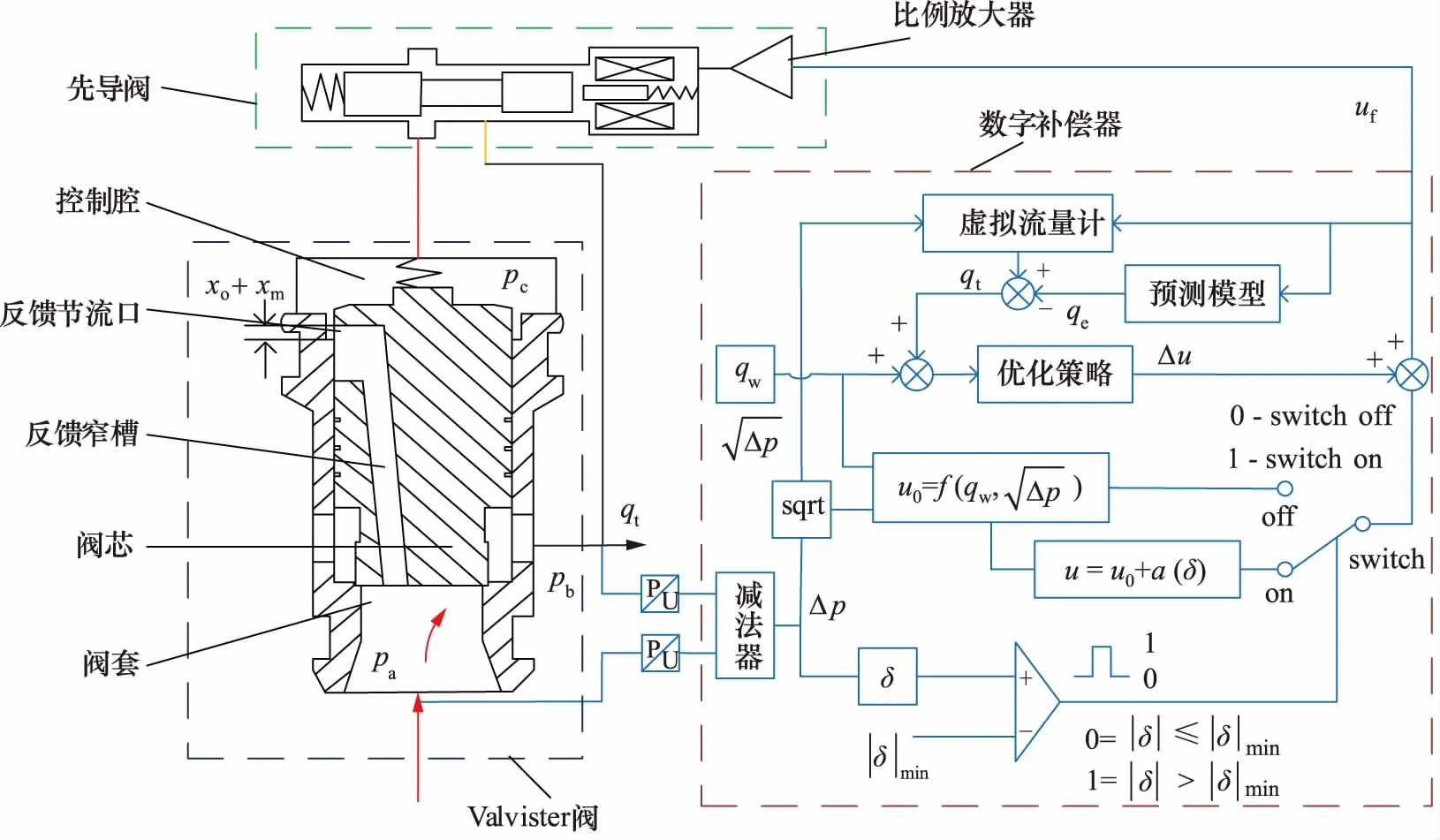
圖1 基于數字補償器的比例調速閥工作原理圖

t時刻主閥口壓力pa,pb由壓力傳感器反饋到數字補償器，設置主閥口壓差變化量以|δ|min為基準，若主閥口壓差變化量小于|δ|min, 只通過GPC對先導閥控制電壓進行補償，不做壓差前饋補償；若主閥口壓差變化量大于|δ|min,則利用期望流量qe、壓差變化量δ經壓差前饋控制器對先導閥控制電進行補償，減小閥芯沖擊。之后將補償后的控制電壓與GPC控制所得控制增量共同作用，對調速閥輸出流量進行精確控制。

2 數學建模

根據力學平衡與流量連續性方程對二級比例插裝閥(Valvistor閥)進行分析，建立其數學模型，推導出數字補償器參數矩陣，設計數字補償器。其中比例調速閥主要參數設置如表1所示。

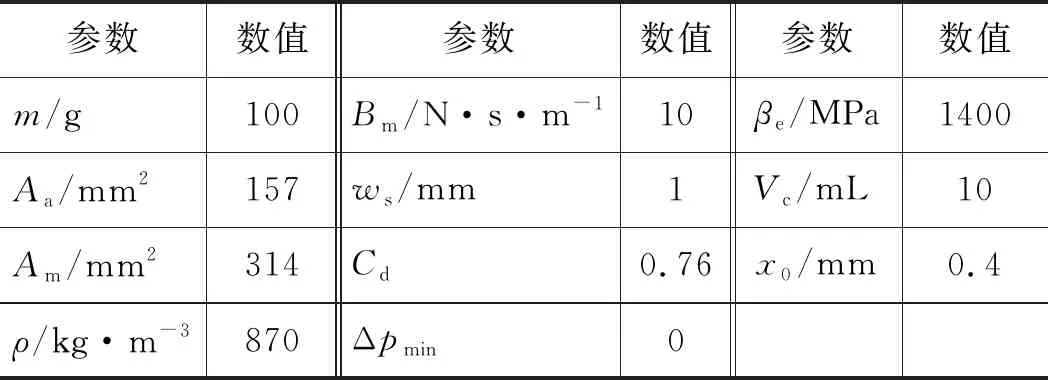
表1 比例調速閥主要參數設置

2.1 Valvistor閥的數學模型

通過主閥口流量qm為：

(1)

wm=π(dm-xm/2)sinα

(2)

式中，Cdm—— 主閥流量系數

wm—— 主閥面積梯度

dm—— 主閥芯直徑

xm—— 主閥芯位移

α—— 主閥芯錐角

ρ—— 油液密度

pa—— 進油口壓力

pb—— 出口壓力

主閥芯動力學方程為：

(3)

式中，m—— 主閥芯質量

Am—— 主閥芯上端面積

pc—— 控制腔壓力

當主閥芯處于穩態，且2Aa=Am時，式(3)可簡化為：

Δp=2Δpp

(4)

由式(3)可知主閥壓差Δp是先導閥壓差Δpp的2倍，其中Δpp=pc-pb，Δp=pa-pb。

忽略先導閥動態特性的影響，先導閥位移與輸入電壓存在以下關系：

xp=kpup

(5)

式中，xp—— 先導閥芯位移

kp—— 比例電磁鐵增益

up—— 先導閥控制電壓

通過先導閥口流量qp為：

(6)

式中，Cdp—— 先導閥流量系數

wp—— 先導閥面積梯度

通過反饋槽流量qs為：

(7)

式中，Cds—— 反饋槽流量系數

ws—— 反饋槽面積梯度

x0—— 主閥芯預開口量

級間流量連續性方程為：

(8)

式中，Vc—— 主閥與先導閥間容腔體積

βe—— 彈性模量

若系統處于穩定狀態，則式(7)可簡化為：

qp=qs

(9)

將式(1)、式(3)、式(6)、式(7)、式(8)進行拉氏變換和小增量線性化處理，分別得到：

Qm=KQmXm

(10)

ms2Xm+BmsXm=-pcAm

(11)

Qp=KQpUp+KPppc

(12)

Qs=KQsXm-KSppc

(13)

(14)

將式(10)、式(12)、式(13)帶入式(14)可得：

(15)

將式(15)帶入式(10)、式(11)可得：

(16)

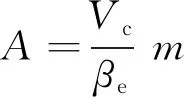
C=Am2+KSpBm+KPpBm

D=AmKQs

K=AmKQpKQm

(17)

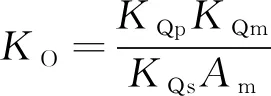
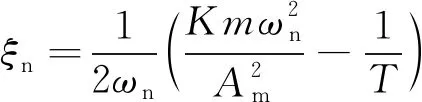
將表1中數據代入式(17)，得到傳遞函數：

(18)

將式(18)進行離散變化：

(19)

式中，a=43.5，b=19.5，c=62，ω=44.3，k=2.29由式(19)可得GPC預測模型的參數矩陣：

A=[1，-1.68，0.82,-0.13,0.01,0]

B=[-0.012，0.016]

(20)

2.2 數字補償器的數學模型

數字補償器由減法器、壓差前饋控制器與GPC控制器組成。主閥進出口壓力由壓力傳感器反饋到減法器計算出實時壓差Δp=pa-pb，與期望流量作用于插值表得到先導閥的控制電壓u0。

在t秒壓差與(t-1)秒壓差差值δ達到設定值時，對控制電壓進行補償：

δ=Δp(t)-Δp(t-1)

(21)

(22)

當|δ|≤0.5 MPa 時，對u0不進行補償，則：

u(t)=u0(t)

(23)

當|δ|>0.5 MPa時，控制器將根據壓差變化量與先導閥控制電壓u0計算出先導閥實時控制電壓u：

u=u0+a(δ)δ>0.5 MPa

u=u0+b(δ)δ<0.5 MPa

(24)

式中，a(δ),b(δ)是關于δ的函數，根據不同的δ值范圍選取不同的值。

壓差前饋控制對負載干擾進行補償的同時引入廣義預測控制作為反饋，加快比例調速閥系統的響應速度與魯棒性。

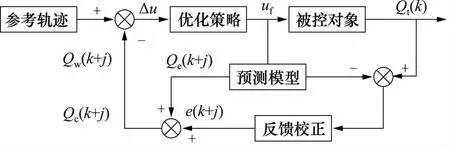
圖2 預測控制結構框圖

廣義預測控制是基于CARIMA模型的多步預測控制，包括預測模型，滾動優化以及反饋校正。預測控制結構框圖如圖2所示。預測模型根據對象的歷史信息和上一采樣點的輸入，預測未來的狀態或輸出。采用了最小方差控制中受控自回歸積分滑動平均模型描述受控模型：

A(z-1)Qe(k)=B(z-1)uf(k-1)+ξ(t)/Δ

(25)

式中，A(z-1)=1+a1z-1+…+anaz-na

B(z-1)=1+b1z-1+…+bnaz-na

Δ=1-z-1—— 差分算子

k—— 采樣控制的離散時間點

q-1—— 后移算子

A，B——q-1的多項式

an，bn—— 多項式的系數

na，nb—— 應其階次

ξ—— 誤差值

Qe—— 預測流量

uf—— 控制電壓

根據GPC原理，利用預測模型，由直到k時刻的的輸入輸出數據，對系統在k+j時刻的最優輸出值Qe(t+j) 進行預測，使用以下丟番圖(Diophantine)方程進行其推導：

(26)

(27)

Ej(z-1)B(z-1)=Gj(z-1)+z-jHj(z-1)

(28)

其中：

Ej(z-1)=e0+e1z-1+…+ej-1z-j+1

Gj(z-1)=g0+g1z-1+…+gj-1z-jv+1

式中,j=1,2,…，為預測步長。

在式(25)兩端乘以ΔEj(z-1)，并將式(26)帶入，得到式(29)：

Qc(k+j)=G(z-1)Δu(k+j-1)+Fj(z-1)·

Qe(k)+Hj(z-1)Δu(k-1)+Ej(z-1)ξ(k)

(29)

其中前三項為最優預測值，最后一項為預測誤差，即：

Qc(k+j)=Qe(k+j)+Ej(z-1)ξ(k)

(30)

最優預測值為：

Qe(k+j)=Gj(z-1)Δu(k+j-1)+

Fj(z-1)Qe(k)+Hj(z-1)Δu(k-1)

(31)

假設系統的期望值為Qw(k+j)，將當前輸出Qt(k)到期望值的參考軌跡進行柔化過渡(0≤α<1)：

Qw(k+j)=αQw(k+j-1)+(1-α)Qt

(32)

在廣義預測控制中優化目的是使預測輸出與參考軌跡的跟蹤誤差最小,此k時刻的優化性能指標如下：

(33)

式中,E—— 數學期望

Qw—— 輸出的期望參考值

N1，N2—— 分別為優化時域的始值與終值

NU—— 控制時域，即在NU步后控制量保持不變

將式(31)、式(32)代入式(33)得到GPC優化控制增量：

Δu(k)=(GTG+λI)-1GT[Qw(k+1)-

FQe(k)-HΔu(k-1)]

(34)

將控制增量與壓差前饋控制得到的控制電壓相加得到：

uf=u(k)+Δu(k-1)

(35)

3 仿真結果分析

本研究主要以16通徑Valvistor閥為模型，溢流閥近似等效負載，如圖3所示，在AMESim中搭建了比例調速閥與壓差前饋控制器仿真模型，如圖4所示在Simulink中搭建廣義預測控制器仿真模型，將模型進行聯合仿真得到比例調速閥的靜動態特性。

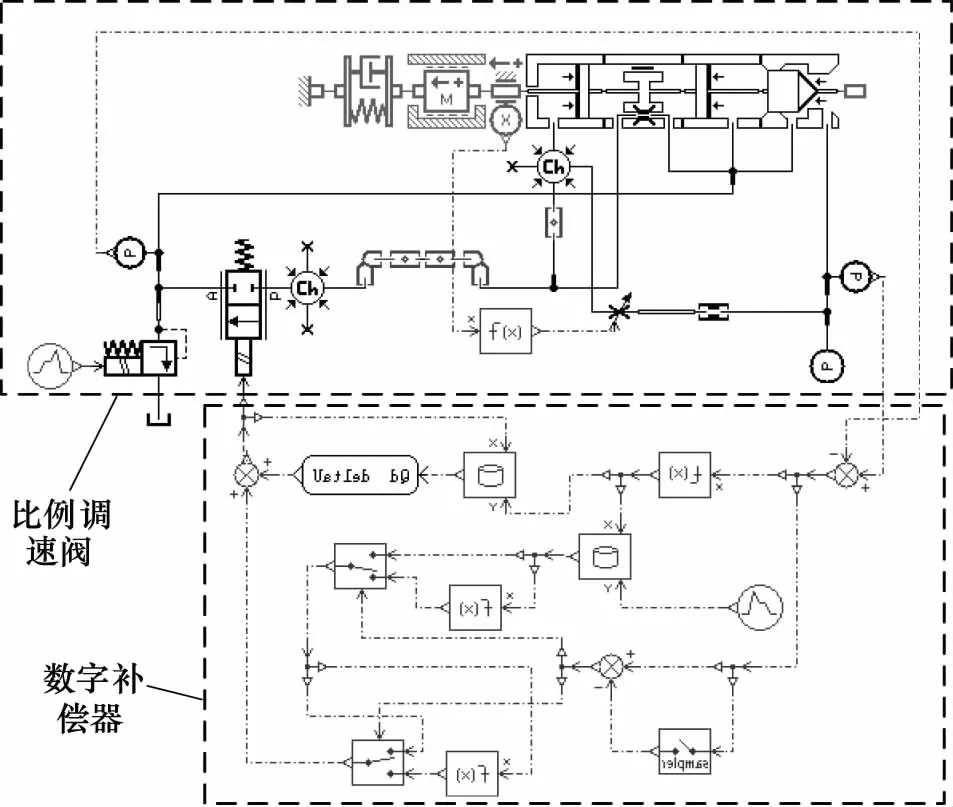
圖3 基于數字補償器的比例調速閥仿真模型

3.1 靜態特性分析

如圖5所示，在保持系統壓差10 MPa恒定不變的條件下，輸出流量與期望流量值正比為1。如圖6所示為靜態負載情況下，改變系統壓差從2 MPa到10 MPa，取4組不同的期望流量值，分別為30, 70, 100, 130 L/min，進行仿真。由仿真結果可知輸出流量基本不受負載變化影響。兩組靜態特性曲線表明比例調速閥在新型數字補償器控制下具有良好的等流量特性。

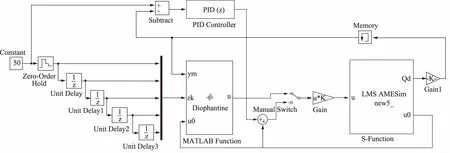
圖4 數字補償器的仿真模型

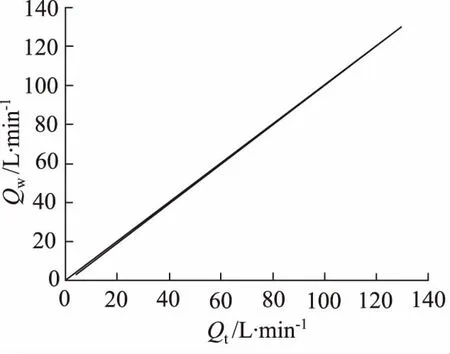
圖5 靜態控制特性曲線

圖6 等流量特性曲線

3.2 動態特性分析

為了更好地驗證本研究所設計的壓差前饋+GPC對流量超調的補償，將其仿真結果與雙線性插值法，閥芯位置反饋PID控制相比較。其中：采樣周期T=0.0001 s，通過多次調整，壓差前饋+GPC控制中預測時域N1=13、控制時域Nu=15、控制加權系數λ=10,柔化因子α=0.1。

輸入期望流量值為50 L/min，保證主閥入口壓力10 MPa不變，當t=0.3 s時改變負載壓力，使主閥進出口壓差由8 MPa階躍為3 MPa時，如圖7a所示, 流量超調量分別為30%，16%,6%，流量超調降低了80%；如圖7b所示，此時閥芯位置動態響應時間分別為0.02, 0.02, 0.015 s；當t=0.7 s改變負載壓力使閥口壓力由3 MPa突變為8 MPa，如圖7c所示, 流量超調量分別為50%，32%，28%，流量超調降低了44%；如圖7d所示，此時閥芯位置動態響應時間分別為0.17, 0.17, 0.013 s。由上述數據分析可知：在相同輸入信號下，當主閥進出口壓差突減，閥芯響應快沖擊小，流量超調小。主閥進出口壓差突增時，閥芯沖擊大，抗負載干擾能力減弱。

當輸入期望流量值為100 L/min時，保證主閥入口壓力如圖8所示，t=0.3 s改變負載壓力，使主閥進出口壓差由8 MPa階躍為3 MPa時，流量超調量分別為32%，27%，24%，流量超調降低了25%。

如圖9所示，t=0. 3 s時,閥芯位置動態響應時間分別為0.02, 0.04, 0.01 s由上述分析可知：輸入信號增大時，閥芯響應速度減慢，流量超調變大。

從仿真結果可知：在相同的工況下，3種控制方法相比，壓差前饋+GPC控制下的Valvistor閥響應速度最快、流量超調最小，具有較高的抗負載干擾能力。

4 結論

提出了新型數字補償器用于比例調速閥流量跟蹤控制。首先，針對負載階躍使比例調速閥發生流量超調使其性能下降的問題設計了壓差前饋控制器，該控制器在檢測到負載突變時能夠快速作用減小主閥芯沖擊。其次將基于離散時間模型的廣義預測控制應用到比例調速閥控制中，提高閥芯響應速度與流量跟蹤性能。通過對Valvistor閥工作原理和數學模型的分析，搭建基于AMESim， MATLAB/Simulink仿真模型并完

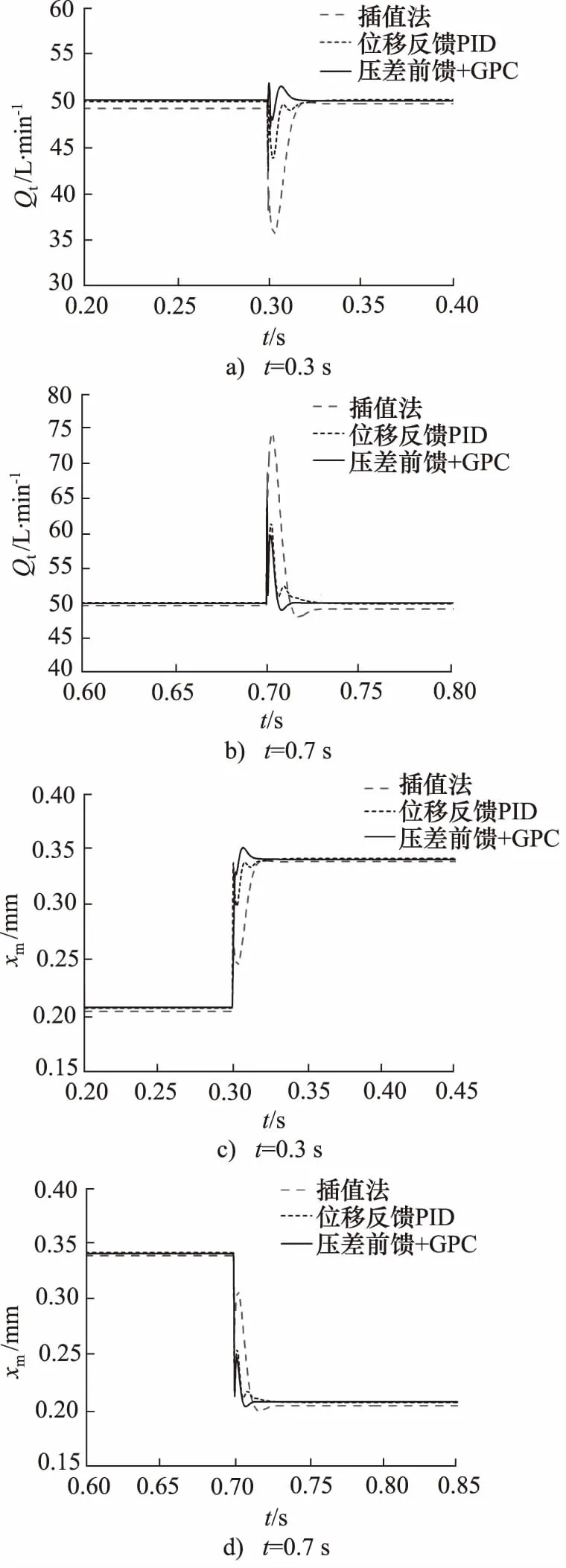
圖7 qw=50 L/min負載壓力階躍曲線

圖8 qw=100 L/min工況下流量曲線

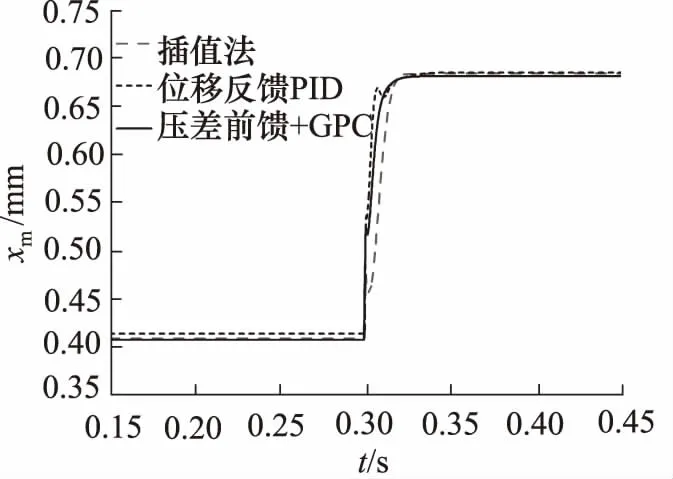
圖9 qw=100 L/min工況下閥芯位移曲線

成仿真驗證，將壓差前饋控制+GPC控制特性與雙線性插值算法控制、位移反饋PID控制特性進行對比。仿真結果證明，提出的新型數字補償器具有良好的流量跟蹤性能，在負載突變時，響應速度最快、流量超調最小，具有較高的抗負載干擾能力，明顯優于另外2種控制方法。另外，該方法中控制器具有一定的自適應性，控制參數容易調節，實用性較強。