基于CFD技術的調速型液力偶合器兩相流分析方法研究

張嘉華， 崔紅偉,2， 常宗旭,2， 廉自生,2， 呂建虎

(1.太原理工大學機械與運載工程學院， 山西太原 030024； 2.太原理工大學煤礦綜采設備山西省重點實驗室， 山西太原 030024； 3.山西晉鼎高科機電設備有限公司， 山西太原 030024)

引言

液力偶合器屬于典型的液力傳動裝置，其主要作用是實現液體能向機械能的轉化，通常安裝于動力機和工作機之間，實現兩者間動力的傳遞。調速型液力偶合器依靠內部工作腔中工作液體的動能來傳遞動力，具有調速節能、隔離緩振、過載保護、空載啟動、可遠程調速等優點。作為柔性傳動環節在與其他工業設備匹配工作時，能夠極大地提升傳動品質。液力偶合器在啟動過程中往往處于部分充液狀態，此時液力偶合器的內流道中流場是包含液體和氣體的復雜氣液兩相環流運動，相比于全充液工況，對于其流場特性的預測更加復雜。同時，啟動工況的轉矩傳遞特性決定了液力偶合器與電機的特性匹配關系和能否實現平穩啟動，這在液力偶合器的實際使用與設計中十分重要[1]。

目前國外學者已經通過成熟的粒子圖像測速(PIV)和激光多普勒測速(LDV)以及應用陣列傳感器等對液力元件內流場分布特性進行研究[2-3]。 DA SILVAA M J等[4]研究了桃形腔偶合器的測試模型，并將平面陣列傳感器安裝在葉輪葉片的吸力面側，以水為工作介質，通過傳感器直接檢測葉片表面的水液分布狀況。HOPPE D等[5]將γ射線成像技術應用于桃形腔的偶合器流場分布特性測試中，獲得了0.25速比，30%充液率時，工作腔內不同軸向剖面的兩相環流的體積率空間分布特性。

由于實驗結果精度不理想、使用成本較高，雖然國內也有一些學者利用流動測試技術對液力元件的流場分布特性進行了研究，但最終獲得的信息比較有限[6]。同時隨著CFD技術的發展和計算機軟、硬件性能的不斷提高，CFD技術開始在液力元件的設計與性能預測上得到更加深入的應用[7-10]。目前國內多數文獻中針對液力元件工作腔流場兩相流動的研究主要基于束流理論，孔令興等[11]在液力緩速器內流場研究中利用束流理論對葉輪的全流道流場數值計算模型進行設計、計算，分析了其轉矩傳遞特性與內部流場分布特性，獲得了較為精確的結果。HUR N等[12]建立了液力偶合器的全流道模型，并利用數值計算方法對不同充液率及不同速比下工作腔內流體的流型進行了預測，并對其成因進行了深入分析。閆清東等[13]利用CFD技術，分別對帶泄漏區與無泄漏區的液力變矩器單流道模型進行穩態數值模擬，通過對比數值計算結果的預測精度，分析了泄漏區損失的影響因素與損失大小的變化趨勢。LIU Chunbao等[14]基于ANSYS Fluent深入分析了尺度解析法(SRS)在多種應用廣泛的液力傳動機械流場分析中的應用，為數值計算過程中常用湍流模型的選用提供了十分可靠的參考數據。魏巍等[15]研究了液力緩速器在低充液率下工作腔內氣相主導的流動規律與降低空轉狀態下的功率損失，基于此，確定低液體填充率擾流柱的有效性的判定方法。

目前，國內外針對礦用調速型液力偶合器的基于CFD技術的兩相流特性分析相對不足，分析結果將為液力偶合器的選型與結構設計提供重要的理論依據。因此本研究選用某型礦用調速型液力偶合器作為研究對象，基于流場數值分析原理，對不同工況條件下的流場體積率分布特性與輸出轉矩特性進行對比分析。

1 控制方程與兩相流模型

由于液力偶合器葉輪的旋轉速度較高，以及葉輪與流場之間存在著劇烈的相互作用，工作室的內部流場是具有復雜流動條件的三維高度湍流。考慮到該液力偶合器具有獨立的散熱系統，同時溫度變化對流場分布與轉矩傳遞影響較小，因此忽略工作過程中流場溫度的變化以及能量耗散，內流場流動滿足動量守恒方程和質量守恒方程[16]。

工作腔內水液和空氣的三維黏性兩相環流的連續方程為：

(1)

αk—— 第k相的體積分數

通過對每一相的動量方程求和，可獲得兩相流動的動量方程，表示為：

(2)

式中，n—— 相數

▽ —— 哈密爾頓算子

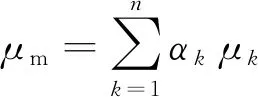
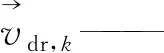
由于礦用調速型液力偶合器的工作特性由流場中水液流動特性所決定，因此在兩相流計算中設定液相(w)為主相，氣相(a)為第二相，滑移速度(即相對速度)定義為氣相的速度相對于液相的速度：

(3)

(4)

根據第二相的連續方程，可知第二相的體積分數方程為：

(5)

在CFD軟件中，Euler方法通常用于計算和處理雙流體模型中每個相的連續介質，也稱為Euler-Euler多相流模型[17]。歐拉-歐拉多相流有如下特點：流體相間連續，在宏觀尺度上各相混合，尺度大于分子尺度，但小于解析尺度(網格尺度)；在CFX中以體積率表示流體的區域相分布情況；每一相有自己的流場參數；各相通過相間的完全相通的計算量傳輸模型進行耦合[18]。

在CFX軟件中針對自由表面流的“歐拉-歐拉多相流”模型又可就不同情況而言細分為2種不同的模型：均一化模型和非均一化模型[19]或稱相間傳遞模型。當兩相之間同享同一速度場、湍流域時，一般宜采用均一化模型模擬；當兩相間具有分界面且有各自不同的速度場、湍流域時，通常采用非均一化模型。液力偶合器一般工作在氣、液相共存的部分充液狀態，且在目前的許多研究中一般均認為氣液兩相為分層流動，在兩相流模型中通過稱為自由表面的交互面實現氣相與液相間物理量的傳遞。因此，選擇非均一化模型用于部分充液狀態的流場模擬。由于礦用調速型液力偶合器的工作特性由流場中水液流動特性所決定，因此在兩相流計算中設定液相為主相，空氣相為附加相，水與空氣之間的表面張力系數設置為0.0726 N/m2。

考慮到兩相流問題求解的復雜性，其求解過程中使用的迭代步數要比一般問題更多，相應的求解時間也更長，收斂難度更大，因此需要采用迎風對流格式和一階湍流方程作為初值的求解條件，并進一步設定高精度對流格式與湍流方程在初值結果的基礎上進行高精度求解。在收斂性的判定上綜合考慮殘差值及流量的不平衡率作為收斂判據。

2 計算分析模型

2.1 數值計算模型

液力偶合器經常工作于不同的速比和充液率下，定義泵輪與渦輪的轉速比i=nT/nP，其中nT為渦輪轉速，nP為泵輪轉速，充液率q為工作腔內充注液體體積VL與工作腔容積V之比，即q=VL/V。圖1顯示了調速型液力偶合器的充液調速工作原理。低充液率時，渦輪轉速較低，水液環流主要在渦輪中，隨著充液率增加，速比同時增大，工作腔中水與空氣的體積比增加，傳遞的扭矩增加，當水液填充率達到100%時進入額定工作狀態。

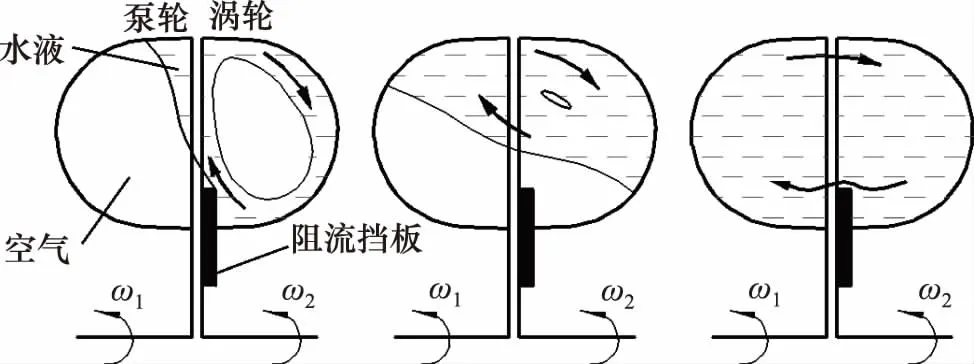
圖1 調速型液力偶合器工作原理

以循環圓外徑D=575 mm的某型礦用調速型雙腔液力偶合器的輸出端葉輪流場為分析模型，葉輪腔形為圓形腔，為了在啟動時獲得一定的限矩能力，在泵輪和渦輪中間安裝有阻流擋板，阻流擋板直徑為循環圓外徑的0.55倍左右。泵輪和渦輪葉片數量分別為46, 45。由于該偶合器的2對葉輪為對稱結構，因此選用其中一對葉輪并獲取其相應的幾何互補模型作為流場進行分析，葉輪與流場的幾何互補模型如圖2所示。

根據葉輪結構的循環對稱的特點，為了提高計算效率，設某葉輪葉片數目為x，利用周期性邊界條件，只需建立其1/x模型即單周期模型作分析就可循環擴展得到整個流場的流線和壓力場分布及整個葉輪的等效應力和整體變形情況，如圖3所示。

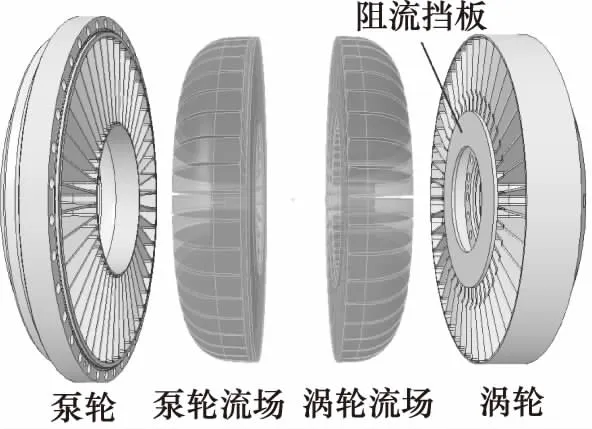
圖2 葉輪與流場幾何模型

圖3 周期循環模型示意圖

利用ICEM軟件，為了保證流場特性計算的準確性與穩定性，采用幾何適應性較強的非結構四面體網格進行流道模型的網格劃分，設定全局網格尺寸為2 mm，建立質量較高的流場網格模型，如圖4所示。

圖4 液力偶合器流道網格模型

2.2 仿真計算條件

由于液力偶合器有專門的循環散熱系統，因此穩態仿真中假設工作水液作等溫流動且不存在流量泄漏，工作水液為不可壓縮的黏性流體，根據先前的研究，液流對葉片的沖擊導致的流道變形較小，可忽略其對流場的影響。同時忽略水液入、出口及葉輪間隙泄漏液流對流場的擾動。泵輪和渦輪內流場之間的界面采用混合入口和出口的邊界條件，考慮到計算成本與求解精度，在CFX軟件中采用基于混合平面模型(Mixing Plane-MP)的級聯法(Stage)對2個流道同時求解，在交界面進行周向平均和交互傳遞，在每一參考框架內均可獲得穩態解。湍流模型采用CFX中具有較高計算精度的SST模型。

為對2種不同兩相流模型下液力偶合器的轉矩特性與流場分布特性進行準確分析，設置泵輪轉速為1475 r/min，在上述流場計算條件下分別對20%, 50%, 80%充液率，0至0.99速比時的流場分布特性與轉矩傳遞特性進行了計算與分析。

3 結果分析

基于CFX軟件分別采用2種不同的兩相流模型進行了流場分析，采用均一化兩相流模型時，氣液混合流體充滿葉輪內流道，采用非均一化模型時流場為氣液分層狀態，因此均一化模型的體積率分布為流道內的均勻分布狀態，在此僅對采用非均一化兩相流模型時的流場體積率分布進行了分析，比較和分析了采用兩種模型所計算的轉矩傳遞特性。

3.1 體積率分布

部分充液工況下，液力偶合器內腔流道內水液分布如圖5所示，其中，淺色區域代表水體積率分布為1，即完全被水液占據。深色區域表示水液體積率為0的區域，即它被氣相占據。兩相交界面處則處于兩相混合交互滲透狀態。圖5b為動輪速比分別為0.2, 0.5, 0.8時，充液率分別為20%，80%時的循環圓軸面體積率分布情況。可見循環圓軸面上氣液兩相呈明顯的分層流動的特點，由于循環圓軸面受葉片攪動和沖擊作用較小，因此在循環圓軸面兩相分布圖中沒有明顯的大面積兩相間滲透現象。

從圖5中可以看出，由于液力偶合器葉輪轉速較大，水密度大于空氣密度，因此在離心力的影響下水液主要分布在循環圓外環。由于泵輪轉速始終大于渦輪，泵輪中水液受到較大的離心力，部分水液被擠壓至渦輪，因此渦輪流道中的水液始終多于泵輪。同時隨著葉輪速比不斷增大，渦輪轉速逐漸提高，渦輪中水液受到的離心力也逐漸增大，因此渦輪中水液所占比例逐漸降低。

如圖6所示，以速比0.2為例，對內流道葉片附近的兩相體積率進行分析。其中圖6a為泵輪葉片壓力面和渦輪葉片非沖擊面的氣-液兩相體積率分布，可見由于泵輪葉片直接帶動水液流動，并且泵輪轉速高于渦輪轉速，渦輪中水液體積率大于泵輪。在較小充液率時(q=0.2)，泵輪葉片壓力面上出現了較為明顯的兩相混合的趨勢。而隨著充液率的增加，水液所占體積率明顯從渦輪葉片非沖擊面向泵輪葉片壓力面、從循環圓外環處小循環向流道大循環發展。圖6b中為泵輪葉片吸力面和渦輪葉片沖擊面體積率分布云圖。由于泵輪加速后流出的高速水液直接沖擊在渦輪葉片沖擊面上， 因此渦輪葉片沖擊面上大部分面積被水液占據，而泵輪葉片吸力面上大部分面積被空氣占據。與圖6a中泵輪葉片沖擊面相比泵輪葉片吸力面體積率更低，而渦輪葉片沖擊面體積率高于非沖擊面。在較高充液率時，由于水液在流道中循環范圍增大，阻流擋板對液流產生了一定的阻擋效果，因此在泵輪壓力面與渦輪沖擊面的流場入口與出口處，相應的產生了低壓區與高壓區，并改變了流場的循環流動趨勢。

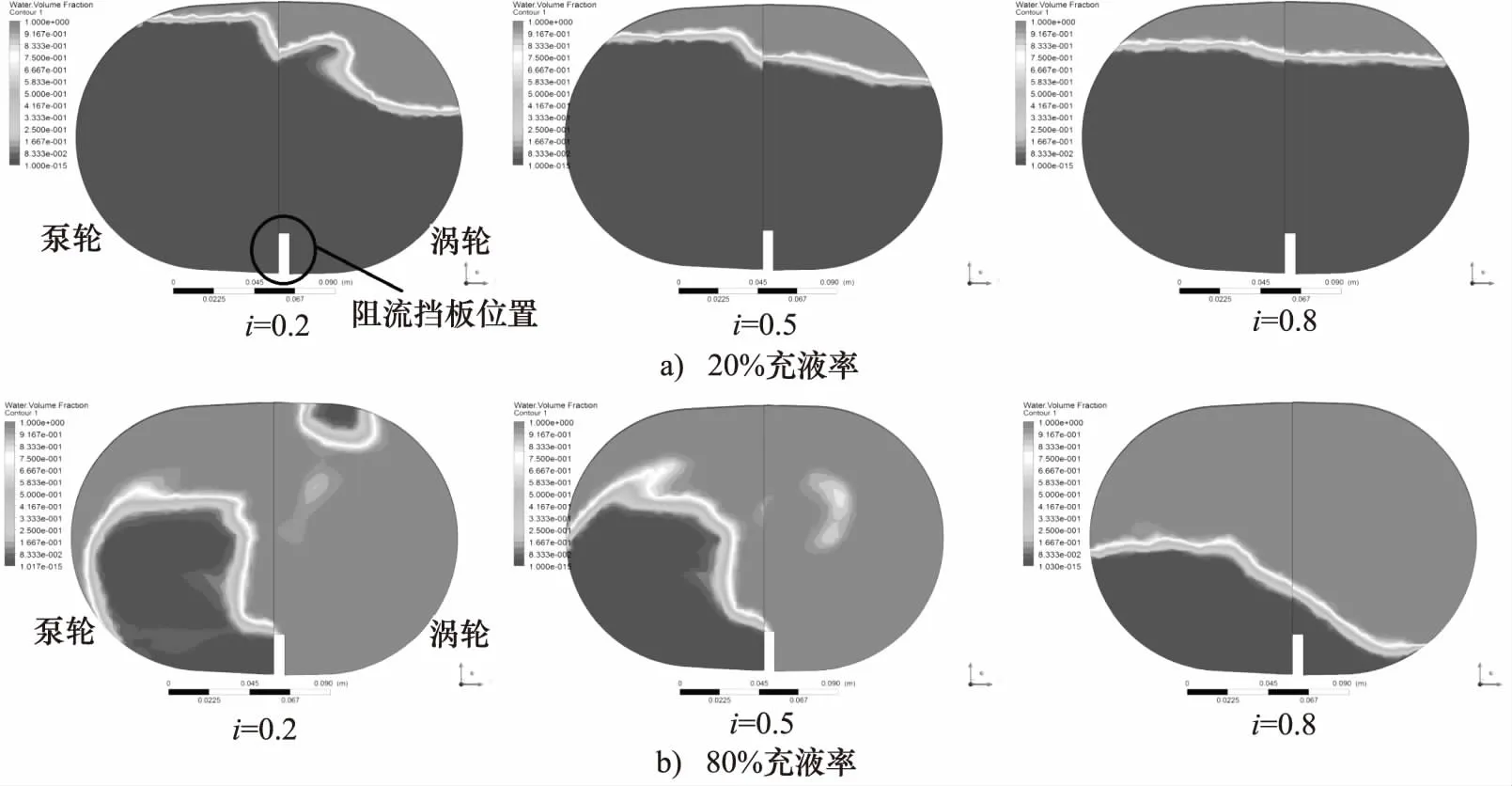
圖5 循環圓軸面容積分布圖

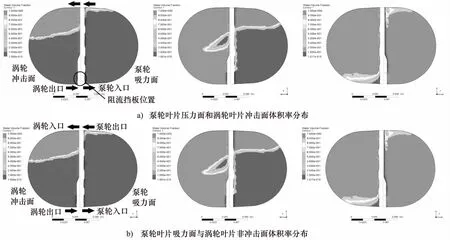
圖6 葉片表面容積分布圖

3.2 轉矩傳遞特性分析

圖7為分別采用2種兩相流模型的調速型液力偶合器輸出端葉輪流場輸出轉矩特性。液力偶合器在速比增大的過程中，泵輪和渦輪流道內水液體積率趨于相等，本質上是由于渦輪轉速增大，渦輪出口水液壓力增大，使泵輪壓力面與吸力面、渦輪沖擊面與非沖擊面壓力差減小，轉矩傳遞特性上表現為偶合器輸出轉矩值隨速比增大不斷減小，并在極限速比時趨于0。同時在較高充液率下，由于隨著速比的升高，液流循環中心逐漸由循環圓內環向循環圓外環移動，阻流擋板對偶合器轉矩的限制作用隨之減小，并在流場不受阻流擋板影響時轉矩下降速度大幅減慢甚至出現一定的回升現象，由于隨著充液率的升高，流場脫離阻流擋板影響的對應速比也不斷增大。為了便于對比分析在20%, 50%, 80%充液率下分別采用均一化模型和非均一化模型兩相流模型，對液力偶合器的轉矩傳遞特性曲線進行預測，結果如圖7所示，非均一化模型計算的不同充液率下的特性曲線體現了一定速比時的轉矩跌落速率減慢或轉矩回升特性，說明了對液力偶合器環流狀態變化預測的準確性。而均一化模型，作為一種簡化的兩相流模型，擁有較高的計算效率，對液力偶合器在較高充液率時的轉矩數值計算結果有一定的參考價值，但無法體現對流場分布及阻流擋板對流場的影響，導致計算的轉矩結果偏高，同時下降趨勢不夠準確。

圖7 轉矩傳遞特性對比曲線圖

4 結論

(1) 本研究應用CFX軟件中的非均一化計算模型對調速型液力偶合器內流道中氣-液兩相流場進行了數值計算，得到了輸出轉矩整體降低并在一定速比時下降速率突降的轉矩傳遞特性，與流場體積率分布特性理論分析結果基本一致，驗證了數值計算方法對流場特性預測的可行性。數值計算結果證明，基于CFD技術的分析方法可用于分析液力偶合器內流場特性。根據從2種兩相流模型獲得的轉矩分析結果，采用非均一化模型獲得的轉矩傳遞特性更準確；

(2) 通過對比3種不同水液充液率及不同轉速比下的氣-液兩相分布特性可得：同一速比時，隨著充液率的升高，氣-液兩相界面的傾斜幅度變大，環流變化趨勢明顯；充液率一定時，隨著速比的升高，渦輪中的水液容積不斷減小，水液環流在達到一定速比時不受阻流擋板的影響。通過對內流場分布特性的分析，對為液力偶合器的結構優化提供了一定的理論依據。