函數圖象變換的規律及應用
陳上太
從高考的命題趨勢來看,函數圖象變換是高考的熱門考點,在函數、三角函數中都有涉及,能綜合考查考生的數形結合能力以及邏輯推理能力.函數圖象的變換主要是指函數圖象的平移變換、伸縮變換、對稱變換等.本文主要總結函數圖象變換的規律,并指導考生運用這些規律去解答相關的高考題.
1 函數圖象變換的規律
1.1 平移變換
1)把函數y=f(x)的圖象向左平移a(a>0)個單位,可得函數y=f(x+a) 的圖象;把函數y=f(x)的圖象向右平移a(a>0)個單位,可得函數y=f(x-a)的圖象;
2)把函數y=f(x)的圖象向上平移b(b>0)個單位,可得函數y=f(x)+b的圖象;把函數y=f(x)的圖象向下平移b(b>0)個單位,可得函數y+b=f(x)(即y=f(x)-b)的圖象.
1.2 伸縮變換

2)函數y=Af(x)(A>0且A≠1)的圖象是把函數y=f(x)的圖象上所有點的縱坐標伸長(當A>1時)或縮短(當0 1)y=f(x)與y=f(-x)的圖象關于y軸對稱; 2)y=f(x)與y=-f(x)的圖象關于x軸對稱; 3)y=f(x)與y=-f(-x)的圖象關于原點對稱; 5)y=f(x)關于點(a,b)對稱的函數是2b-y=f(2a-x) (即y=2b-f(2a-x)). 將函數y=sinx依次進行如下變換: A. 3x-2y+2=0 B. 2x+3y+7=0 C. 3x-2y-12=0 D. 2x+3y+8=0 (1)寫出曲線C1的方程; y=(x-t)3-(x-t)+s. (2)在曲線C上任取一點B1(x1,y1),設B2(x2,y2)是B1關于點A的對稱點,則有 所以x1=t-x2,y1=s-y2. 代入曲線C的方程,得x2和y2滿足方程: s-y2=(t-x2)3-(t-x2), 即 y2=(x2-t)3-(x2-t)+s. 故點B2(x2,y2)在曲線C1上. 反過來,同樣可以證明在曲線C1上的點關于點A的對稱點在曲線C上.因此,曲線C與C1關于點A對稱.1.3 對稱變換
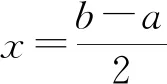
2 函數圖象變換規律的應用
2.1平移變換



2.2 平移和伸縮變換


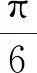
2.3 對稱變換


2.4 平移與對稱變換




