一種基于切換拓撲的離散時間一致性協議

杜宇凡

(廣東工業大學計算機學院 廣東省廣州市 510006)

近年來，多智能體系統協同控制方面的研究取得了突破性的進展。一致性協議是多智能體理論中的一個核心問題。設計一致性協議旨在使得智能體狀態在協議控制下最終能達到一致性。

Krause等人[1]提出了一種基于切換拓撲的離散時間一致性協議，即經典的Hegselmann—Krause模型，各智能體取其通信范圍內的鄰居智能體的狀態平均值作為下一次迭代狀態。在該協議下，多智能體系統通常不能始終保持連通，系統最終會演化成多個小群體，每個小群體之間的距離超過通信范圍，不再相互通信。

Zheng等人[2]提出了一種基于切換拓撲的離散時間一致性協議，各智能體取其自身狀態與通信范圍內的鄰居智能體的組合狀態作為下一次迭代狀態。Zheng[2]等人證明了，在該協議下，如果多智能體系統能始終保持連通，且調整因子滿足小于時，系統最終能收斂到全局的狀態平均值。

Xie等人[3]提出了一種基于切換拓撲的離散時間一致性協議，各智能體取其自身狀態與通信范圍內的最近鄰居智能體的組合狀態作為下一次迭代狀態。該方法只需考慮兩側的最近鄰居智能體的狀態信息，大大減少了計算量。Xie等人[3]證明了，在該協議下，如果多智能體系統能始終保持連通，且調整因子滿足小于時，系統最終能收斂到全局的狀態平均值。調整因子的范圍進一步擴大，這樣有助于加快系統的收斂速度。

然而，怎樣才能保證多智能體系統始終保持連通？上述一致性協議都沒有涉及到這個關鍵問題。一旦系統在演化過程中喪失了連通性，智能體的狀態值就不能達成一致。本文從保持連通性的角度出發，設計了一種改進的Hegselmann-Krause一致性協議，使得多智能體系統可以始終保持連通，并最終一定能達成一致。

本文的章節安排如下：II章節主要介紹一些閱讀本文所必需的基礎知識，包括圖論與矩陣論，離散一致性協議等等，并在末尾對本文研究的主要問題做了簡單的闡述。III章節陳述了本文的主要結果，提出了一種基于切換拓撲的離散時間一致性協議。IV章節通過仿真實驗驗證了該協議的有效性。最后，V章節給出了本文的結論和未來的研究展望。

1 預備知識及問題描述

1.1 圖論與矩陣論

我們把一個具有n個智能體的多智能體系統描述為一個具有n個頂點的無向圖其中V是圖G的頂點集，滿足是頂點的順序標號。E是圖G的邊集，滿足圖G的一條邊表示一對頂點i和j互為鄰居，鄰居之間可以彼此接收到對方發送出的信息。頂點i的鄰居集可表示為是圖G的鄰接矩陣，其元素與邊相關：。

引理 圖G的拉普拉斯矩陣L具有以下性質：

（1）0是矩陣L的一個特征值，1是其對應的特征向量，滿足L1=0；

（2）如果圖G是連通無向圖，那么0是矩陣L的單一特征值；

（3）如果圖G是連通無向圖，那么矩陣L是對稱正半定矩陣且有n個非負實數特征值，可按升序排列為其中被稱為圖G的代數連通度。

1.2 離散一致性協議

考慮一個具有n個智能體的多智能體系統，這些智能體的狀態值處于一個實數集R。我們用G={V,E,A}表示智能體所對應的圖結構，每個智能體的狀態值用xi(k)表示，其中k為迭代次數。

Krause等人[1]提出了一種基于切換拓撲的離散時間一致性協議：

即智能體i下一次的狀態為所有鄰居智能體（包括自身）的狀態平均值。系統不能達成一致性，會演化成多個觀點值。

Zheng等人[2]提出了一種基于切換拓撲的離散時間一致性協議：

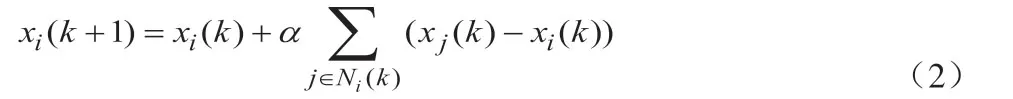
即智能體i下一次的狀態為其自身狀態與通信范圍內的鄰居智能體的組合狀態。Zheng[2]等人通過李雅普諾夫函數理論證明了在該協議下，若多智能體系統能始終保持連通，且調整因子a滿足小于時，系統最終能收斂到全局的狀態平均值。

Xie等人[3]提出了一種基于切換拓撲的離散時間一致性協議：

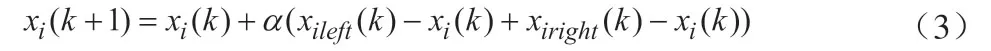
即智能體i下一次的狀態為其自身狀態與通信范圍內的最近鄰居智能體的組合狀態，是智能體i兩側的最近鄰居智能體的狀態。Xie等人[3]通過李雅普諾夫函數理論證明了在該協議下，若多智能體系統能始終保持連通，且調整因子a滿足小于時，系統最終能收斂到全局的狀態平均值。以上兩個一致性協議(2),(3)都是假設系統能保持連通，但是系統往往不能始終保持連通。一旦系統連通性不能保持，一致性就不能達成。我們在下文中提出了一種離散一致性協議，保證系統能始終保持連通，并能穩定地達成一致性。

1.3 問題描述

對于任意的智能體初始狀態向量x(0)，和智能體i,j=1,...,n，如果存在離散一致性協議使得各智能體狀態在有限次迭代次數內最終趨于一致，則稱該協議解決了一致性問題。

2 主要結果

我們給出如下定義：

智能體i下一次的狀態為自身狀態和兩側最遠鄰居智能體狀態的平均值。若智能體i的左鄰域為空集，即左側沒有最遠鄰居，則忽略左鄰域，只考慮右側的最遠鄰居；若智能體i的右鄰域為空集，即右側沒有最遠鄰居，則忽略右鄰域，只考慮左側的最遠鄰居。

以上描述用一致性協議描述如下：

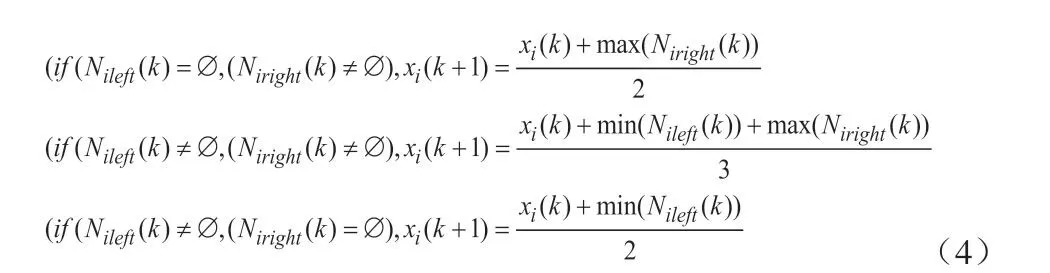
接下來，我們將證明，對于初始時刻連通的初始拓撲，在一致性協議（4）下系統一定能保持連通性，并最終一定能達成一致性。

定理1：如果兩個智能體i,j在第k次迭代中具有相同的狀態，那么這兩個智能體i,j在第k+1次迭代中具有相同的狀態。即如果

證明：如果兩個智能體i,j在第k次迭代中具有相同的狀態，它們就有著相同的兩側最遠鄰居，那么在k+1次迭代中，兩個智能體i,j也會具有相同的狀態。

特別地，如果兩個智能體i,j在第k次迭代中具有相同的狀態，那么它們在隨后的迭代中就有相同的狀態。

定理2：對于初始時刻連通的初始拓撲，在第k次迭代中，邊界智能體（狀態值最大的和最小的智能體）有且僅有一個鄰居，其余智能體有且僅有兩個鄰居。狀態值最小的智能體，其左鄰域為空集，在右鄰域上有且僅有一個鄰居；狀態值最大的智能體，其右鄰域為空集，在左鄰域上有且僅有一個鄰居。

證明：基于初始時刻連通的初始拓撲，對于除了邊界智能體以外的智能體，它們在左右鄰域上一定能搜索到智能體作為它的鄰居，所以它們一定會有兩個鄰居。而狀態值最小的智能體在左鄰域上搜索不到鄰居，只有在右鄰域上能搜索到鄰居；狀態值最大的智能體在右鄰域上搜索不到鄰居，只有在左鄰域上搜索到鄰居。

定理3：對于初始時刻連通的初始拓撲，假設有兩個非邊界智能體i,j，滿足那么智能體i,j在其左右鄰域的最遠鄰居滿足：

定理4：對于初始時刻連通的初始拓撲，在一致性協議（4）下系統一定能保持連通性。即如果系統在第k次迭代中是連通的，系統在第k+1次迭代中就一定是連通的。

證明：假設在第k次迭代中系統n個智能體的狀態值為

由于系統在第k次迭代中是連通的，因此依次有序的兩智能體的狀態值的差值均小于r，即

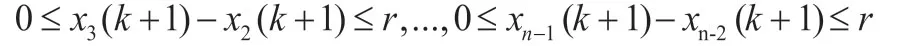
則根據定理2，智能體i和j均有兩個鄰居，那么有

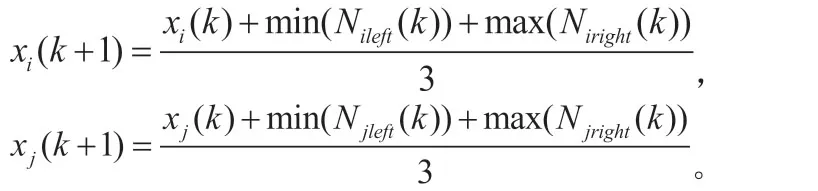
然后我們討論邊界智能體xn(k)在k+1次迭代中可能會發生的情況。

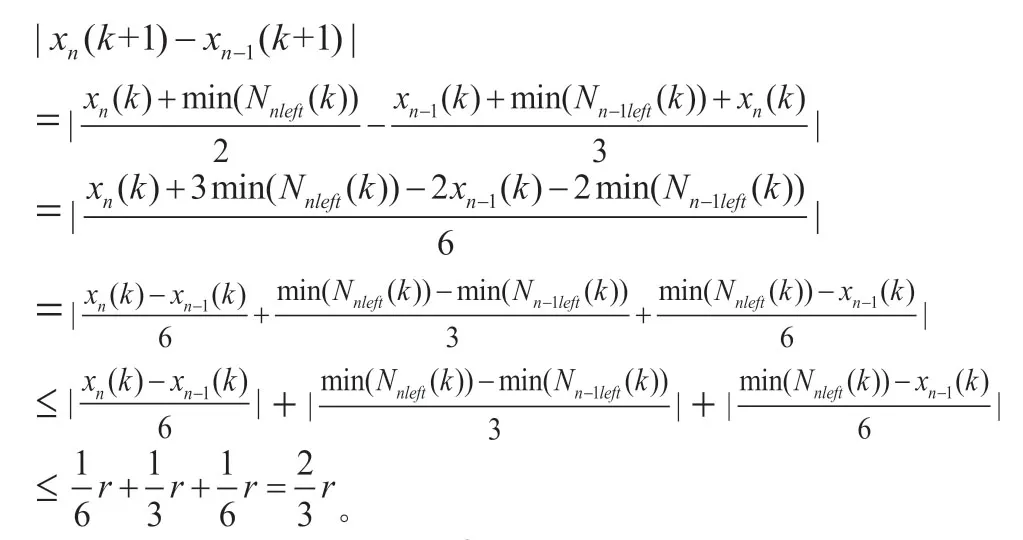
于是我們可知，如果系統在第k次迭代中是連通的，系統在第k+1次迭代中就一定是連通的。證畢。

定理5：對于初始時刻連通的初始拓撲，在一致性協議（4）下系統一定能達成一致性。

證明：我們首先證明，在每一次的系統迭代中，系統的最大狀態值單調遞減，系統的最小狀態值單調遞增。

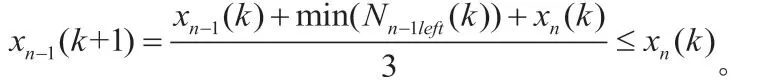
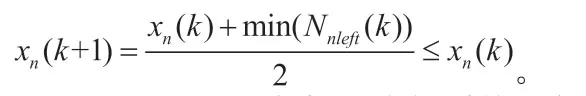
于是我們又在每一次的系統迭代中，系統的最大狀態值單調遞減，類似地，系統的最小狀態值單調遞增。系統的區間長度在不斷減小。

而根據定理4，系統在迭代過程中又能一直保持連通，那么在有限次的迭代次數中，必定存在一個迭代次數t，使得系統的區間長度小于r。

當到達這個迭代次數t時，狀態值最大的智能體在左鄰域上選擇的鄰居就是狀態值最小的智能體，狀態值最小的智能體在右鄰域上選擇的鄰居就是狀態值最大的智能體。于是，在t+1次迭代中，這兩個智能體的狀態發生了重合，它們的狀態值等于在t次迭代中這兩個智能體的狀態平均值。

在后續的迭代次數中，系統的區間長度仍在不斷減小。但是系統中智能體的狀態值至少會兩兩重合一次。那么經過有限次的迭代次數后，系統中的所有智能體的狀態值會完全相同，即系統一定能達成一致性。

于是我們可知，對于初始時刻連通的初始拓撲，在一致性協議（4）下系統一定能達成一致性。證畢。

3 仿真實驗

本文的仿真實驗是基于Matlab數學軟件來進行的。在仿真實驗中，以智能體的位置信息作為狀態值，以智能體進行匯聚為例，考慮初始時刻系統的初始拓撲是連通的。我們以Xie等人在[3]中提出的基于切換拓撲的離散時間一致性協議作為對比對象，主要討論本文提出的一致性協議和該協議在性能上的共同點和不同點。

對于兩種一致性協議而言，每一個智能體在進行狀態演化的過程中，都只需要存儲和計算自身和兩個鄰居智能體的狀態信息（[3]中的協議（3）是選擇兩個與自身狀態差值最近的智能體，而本文是選擇兩個與自身狀態差值最遠的智能體），因此在每一步的迭代過程的計算量都只需要兩次，兩種協議在系統演化所需要的計算資源上是相同的。

但是，當系統的初始拓撲是隨機分布的情形時，[3]中的協議不一定能保證系統拓撲在智能體的狀態演化過程中始終保持連通，系統拓撲可能不會收斂到一致性。而本文提出的一致性協議（4），經過了嚴格的證明分析，無論系統的初始拓撲是何種情形，系統拓撲在智能體的狀態演化過程中一定能保持連通，并能收斂到一致性。而且，本文的鄰域選取策略是選擇兩個與自身狀態差值最遠（而非最近）的鄰居智能體，因此一致性協議（4）的收斂速度上比[3]中的協議（3）有較明顯的加快。

接下來，我們通過對[3]中的一致性協議（3）和本文提出的一致性協議（4）進行四組仿真實驗，作出對比分析。每一組仿真實驗中智能體的初始狀態信息是相同的，即1)和2），3)和4)，5)和6)，7)和8)中的多智能體系統具有相同的初始拓撲。

1.一致性協議（3）：11個智能體的狀態值均勻分布在[0,5]的區間內，通信半徑r=1，調整因子。在智能體的狀態演化過程中系統拓撲始終保持連通，經過約100次迭代后，11個智能體的狀態值達成一致，匯聚在一個點2.5上，具體情況如圖1所示。

2.一致性協議（4）：11個智能體的狀態值均勻分布在[0,5]的區間內，通信半徑r=1。在智能體的狀態演化過程中系統拓撲始終保持連通，經過約15次迭代后，11個智能體的狀態值達成一致，匯聚在一個點2.5上，具體情況如圖2所示。

3.一致性協議（3）：20個智能體的狀態值均勻分布在[0,10]的區間內，通信半徑r=1，調整因子。在智能體的狀態演化過程中系統拓撲始終保持連通，經過約300次迭代后，20個智能體的狀態值達成一致，匯聚在一個點5上，具體情況如圖3所示。

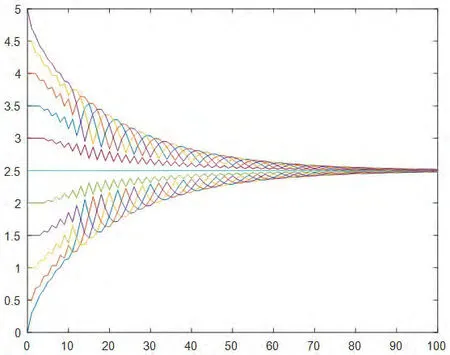
圖1：協議（3）下初始拓撲均勻分布在區間[0,5]的演化過程

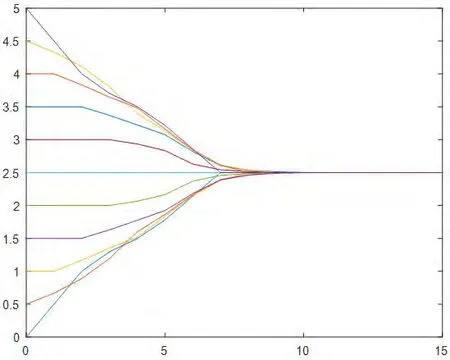
圖2：協議（4）下初始拓撲均勻分布在區間[0,5]的演化過程

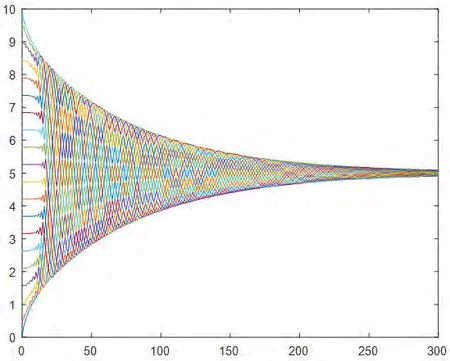
圖3：協議（3）下初始拓撲均勻分布在區間[0,10]的演化過程

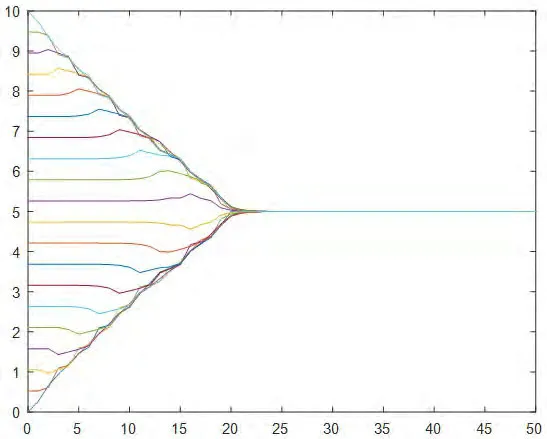
圖4：協議（4）下初始拓撲均勻分布在區間[0,10]的演化過程

4.一致性協議（4）：20個智能體的狀態值均勻分布在[0,10]的區間內，通信半徑r=1。在智能體的狀態演化過程中系統拓撲始終保持連通，經過約50次迭代后，20個智能體的狀態值達成一致，匯聚在一個點5上，具體情況如圖4所示。

5.一致性協議（3）：11個智能體的狀態值隨機分布在[0,5]的區間內，通信半徑r=1，調整因子。在智能體的狀態演化過程中系統拓撲不能始終保持連通，經過約50次迭代后，11個智能體的狀態值分裂成兩個集群，分別是點0.9和點3.4，具體情況如圖5所示。

6.一致性協議（4）：11個智能體的狀態值隨機分布在[0,5]的區間內，通信半徑r=1。在智能體的狀態演化過程中系統拓撲始終保持連通，經過約15次迭代后，11個智能體的狀態值達成一致，匯聚在一個點2.5上，具體情況如圖6所示。

7.一致性協議（3）：20個智能體的狀態值隨機分布在[0,10]的區間內，通信半徑r=11，調整因子。在智能體的狀態演化過程中系統拓撲不能始終保持連通，經過約80次迭代后，20個智能體的狀態值分裂成四個集群，分別是點1.3，點3.2，點5.8和點8，具體情況如圖7所示。

8.一致性協議（4）：20個智能體的狀態值隨機分布在[0,10]的區間內，通信半徑r=1。在智能體的狀態演化過程中系統拓撲始終保持連通，經過約50次迭代后，20個智能體的狀態值達成一致，匯聚在一個點4.8上，具體情況如圖8所示。

通過以上仿真，可以觀察到，當系統的初始拓撲是隨機分布時，系統拓撲可能不能始終保持連通性，因而會分裂成多個集群。而在本文提出的一致性協議（4）下，無論系統的初始拓撲是均勻分布還是隨機分布，系統拓撲在智能體的狀態演化過程中一定能保持連通，并且各智能體的狀態值一定能漸近收斂到初始時刻的全局幾何中心，即達成一致性。而且，由于智能體的鄰域選取策略是選擇兩個與自身狀態差值最遠（而非最近）的鄰居智能體，系統的收斂速度明顯加快。

4 結束語

在本文中，我們針對通信范圍有限的多智能體系統，提出了一種離散時間一致性協議。在一維情形下，對于任意初始時刻連通的初始拓撲，基于該協議，智能體都能保持連通性，并一定能漸近收斂到它們的初始狀態平均值。

我們未來的工作是設計一個更好的切換拓撲下的離散時間一致性協議。有三點值得進一步研究：

（1）尋找更好的方法來保持切換拓撲的連通性；

（2）設計更簡潔合理的一致性協議；

（3）更快的收斂速度。

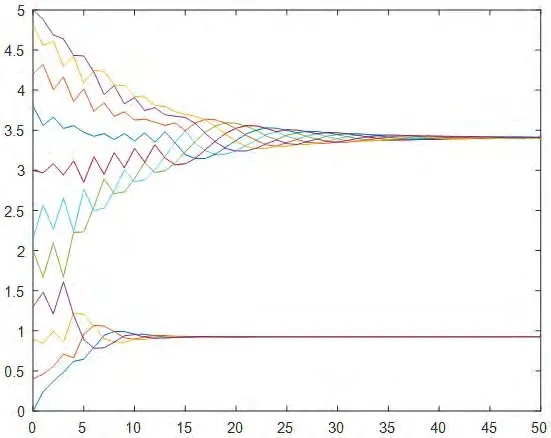
圖5：協議（3）下初始拓撲隨機分布在區間[0,5]的演化過程

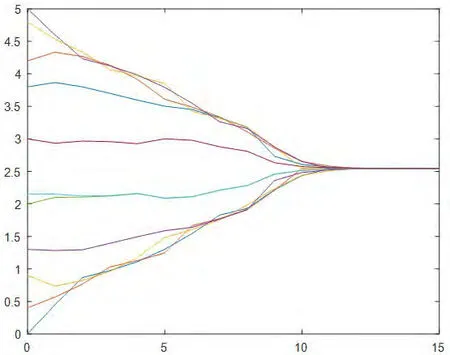
圖6：協議（4）下初始拓撲隨機分布在區間[0,5]的演化過程

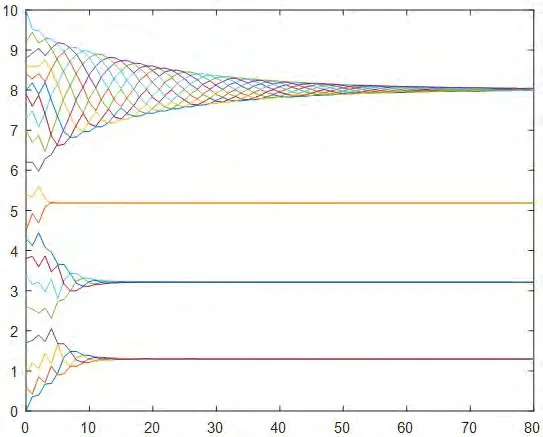
圖7：協議（3）下初始拓撲隨機分布在區間[0,10]的演化過程

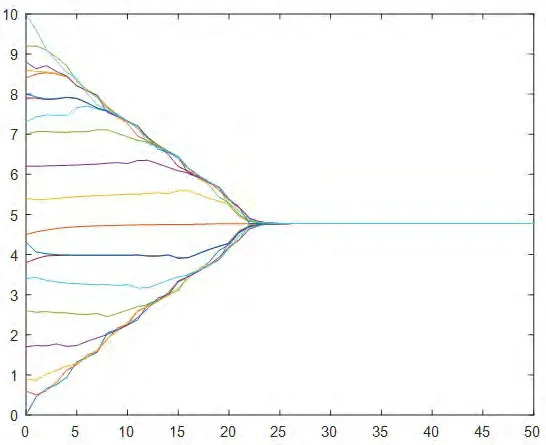
圖8：協議（4）下初始拓撲隨機分布在區間[0,10]的演化過程