研磨介質形狀對球磨機特性影響的DEM 模擬研究

浙江大學能源工程學院化工機械研究所 浙江杭州 310027

在 球磨機的工作過程中，研磨介質對于球磨機工作特性的影響主要表現在研磨介質的形狀、大小和填充率等方面。為了提高球磨機的工作效率，選取合適的研磨介質非常重要。目前球形研磨介質和圓柱形研磨介質的應用最為廣泛。隨著近年來計算機技術的蓬勃發展，在顆粒體系的研究中，離散單元法 (Discrete Element Method，DEM) 逐漸走入人們的視野，該方法在顆粒的混合分離[1]、物料破碎[2]及氣固兩相流動耦合[3]研究等許多領域得到了應用。Mishra 和Rajamani 首次利用二維 DEM 模型對球磨機內的顆粒運動進行研究[4]；隨后，Cleary 也利用該方法研究了球磨機轉速對顆粒行為 (如轉矩、功率等方面) 的影響[5]。為了使模擬過程更加接近實際情況，Cleary 首次利用三維 DEM 模型[6-7]來預測球磨機的能量損耗，并對于該模型的精確度做出了驗證[8]；隨后基于該模型，研究人員在填充率、轉速和提升條的形狀及數量，以及顆粒的材料特性等方面進行了許多研究[9-11]。

由于非球形研磨介質的建模難度較大，過去研究人員多針對球形研磨介質，采用 DEM 模型進行模擬。在球磨機實際操作過程中，非球形研磨介質的應用范圍也非常廣泛，而目前仍然缺少對非球形研磨介質與球形研磨介質在球磨機內顆粒行為差異的系統性研究。筆者在超橢球模型[12-13]的基礎上，建立了 4 種不同形狀的顆粒模型 (包括 1 種球形顆粒及 3 種圓柱形顆粒)，首先驗證了離散單元法預測球磨機內研磨介質運動的精度，隨后對不同形狀研磨介質在球磨機內的工作過程進行模擬，對其在功率、運動特性、碰撞能量及磨損等方面的差異進行了比較。

1 研究方法

1.1 研磨介質模型

在三維笛卡爾直角坐標系中，當超橢球中心位于坐標原點、主軸位于坐標軸上時，得到的曲面方程稱為超二次曲面方程[14]，其標準公式為

式中：a、b、c為顆粒沿主軸方向的半軸長；s1、s2為形狀參數，選取不同的形狀參數可以得到不同形狀的封閉曲面。

圖1 所示為 4 種研磨介質，其相應的尺寸參數如表 1 所列。

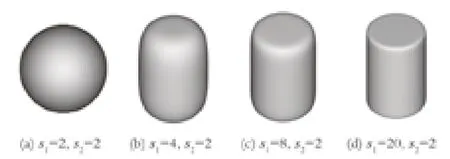
圖1 4 種研磨介質Fig.1 Four kinds of grinding media

1.2 研磨介質運動方程

DEM 中的研磨介質運動方程遵循牛頓運動定律，對于球磨機內的單個研磨介質i，其瞬時運動狀態由 2 種力決定，分別為接觸力和重力。

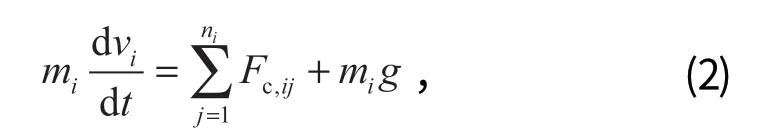
式中：mi為研磨介質的質量；Fc,ij為研磨介質i和j的接觸力 (j可以是與i碰撞的研磨介質或襯板)；ni為碰撞次數；g為重力加速度。

研磨介質的旋轉由其轉矩決定，

式中：Ii為慣性張量；Tc,ij為接觸轉矩；ωi為角速度。

球形研磨介質由于具有對稱性，其慣性張量Ii和接觸轉矩Tc,ij很容易通過計算得到。然而當非球形研磨介質旋轉時，全局坐標系中的慣性張量Ii是隨時間變化的，所以非球形研磨介質的慣性張量Ii和接觸轉矩Tc,ij難以通過同樣的計算方法得到。為了解決這個問題，需要一個局部坐標系：首先，在全局坐標系中確定的接觸轉矩Tc,ij通過旋轉矩陣轉換成局部坐標系，一旦研磨介質之間發生接觸，通過標準的軟球線性彈簧-阻尼模型[15]就可以確定研磨介質之間的接觸力，然后再通過這些接觸參數計算接觸轉矩；隨后，利用轉換矩陣將局部坐標系下的旋轉運動用全局坐標系來表示，并確定非球形研磨介質在全局坐標系中的位置。眾多研究[16-19]已對非球形顆粒在 DEM 框架內的建模進行了描述，在此不再詳述。

1.3 接觸模型

為了計算研磨介質之間的接觸力，采用線性彈簧-阻尼模型[15]。研磨介質i和j之間的法向接觸力Fc,n,ij和切向接觸力Fc,t,ij分別為

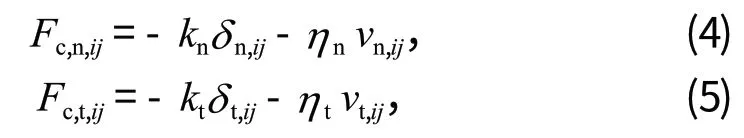
式中：kn、kt分別為法向彈簧剛度和切向彈簧剛度；δn,ij、δt,ij分別為 2 個接觸研磨介質間的法向位移和切向位移；ηn、ηt分別為法向阻尼系數和切向阻尼系數；vn,ij、vt,ij分別為研磨介質之間的法向相對速度和切向相對速度。

當 2 個接觸的研磨介質 (或研磨介質和襯板) 之間發生滑動，滿足以下等式時：

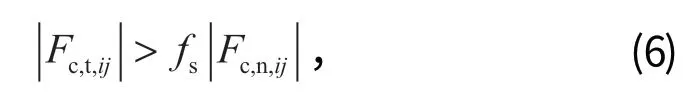
采用庫侖摩擦模型來計算切向接觸力

式中：Tc,n,ij、Tc,t,ij分別為由法向接觸力和切向接觸力引起的轉矩；L為從研磨介質中心到接觸點的距離矢量；Tc,r,n,ij、Tc,r,t,ij分別為通過滾動產生的法向轉矩和切向轉矩，滾動軸的方向分別與法向接觸力平行和垂直；kr,n,ij、kr,t,ij分別為法向和切向扭轉約束剛度；αn,ij、αt,ij分別為 2 個接觸研磨介質之間的法向和切向扭轉位移；ηr,n,ij、ηr,t,ij分別為法向和切向扭轉阻尼系數；ωn,ij、ωt,ij分別為接觸磨介在法向和切向上的相對角速度。

當法向轉矩和切向轉矩滿足以下關系時：

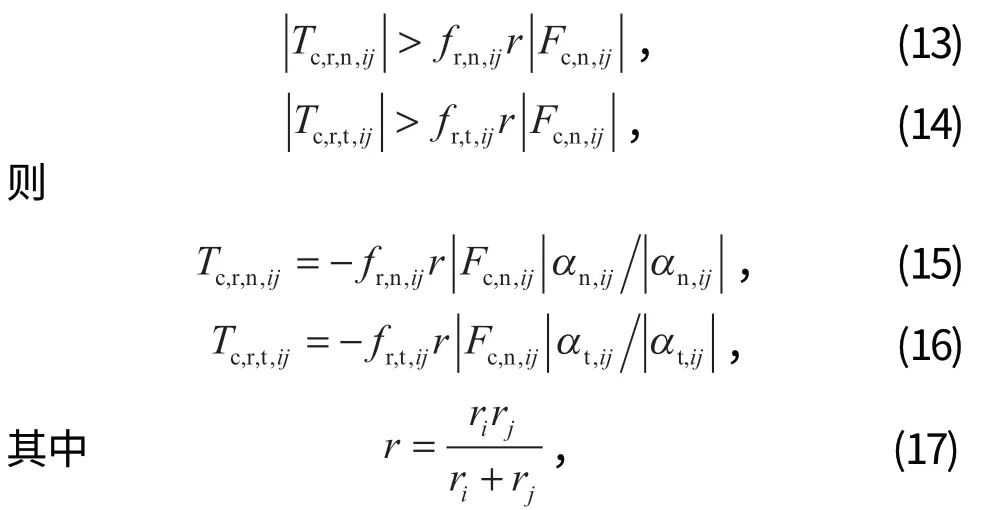
式中：fr,n,ij和fr,t,ij分別為法向和切向滾動摩擦因數；r為研磨介質的有效半徑；ri和rj為 2 個接觸的研磨介質i和j的等效半徑，如果是研磨介質與壁面接觸，則有效半徑即為研磨介質的半徑。

1.4 磨損模型

采用剪切沖擊能量模型 (SIEM)[20]計算球磨機襯板的磨損。撞擊后襯板表面的損失量

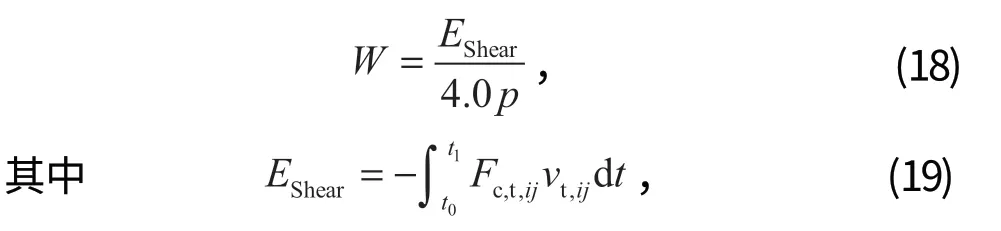
式中：EShear為剪切沖擊能量；p為接觸面的塑性流動壓力，通常是維氏硬度的 1～5 倍；t0、t1分別為研磨介質開始接觸的時間和分開的時間。

在沖擊期間，累積計算由表面吸收的剪切沖擊能量EShear，并在以下兩式同時成立時計算磨損：Fc,t,ij vt,ij< 0，Fc,t,ij vij< 0。

根據 Finnie 等人的試驗數據[21]，鋼材的塑性流動壓力設置為維氏硬度的 1.5 倍。關于剪切沖擊能量模型 (SIEM) 的更多細節可以參考我們之前的論文[20，22]。

2 模擬參數及計算條件

為了驗證 DEM 對球磨機內研磨介質行為預測的準確性，選取 Bian 等人[23]的試驗進行模擬驗證。試驗選取內徑為 573 mm、軸向長度為 160 mm 的球磨機，球磨機滾筒內部裝有 24 個高度為 10 mm、頂部寬度為18 mm 的提升條。模擬時選取與試驗相同的設備。

選用的研磨介質基于超橢球模型構建。如前文所述，當s1=s2=2 且a=b=c時，研磨介質為標準的球體；保持s2=2 不變，增大s1的值，研磨介質的邊緣表現得越來越尖銳，且整體形狀上越來越趨向于圓柱體。圖 1 所示的 4 種研磨介質的s1值分別為 2、4、8 和 20，s2值均為 2。對于s1為 4、8、20 的研磨介質，設定c=1.5a=1.5b，這樣可以得到長徑比均為1.5 的 3 種近似圓柱體的研磨介質。除此之外，將每種形狀的研磨介質分成等效直徑分別為 8、13、15 和 20 mm 的 4 組，得到 16 種不同的研磨介質，具體如表 1所列。

在 5 種不同的球磨機轉速條件下，對每種研磨介質進行模擬，球磨機轉速分別為 33.45、39.02、41.82、44.60 和 50.18 r/min，即球磨機臨界轉速的60% (球磨機轉速與臨界轉速的百分比用ψ表示)、70%、75%、80%、90%。利用自行開發的 DEM 程序進行模擬，其優勢在于可以精確描述非球形顆粒的形狀，并在保證模擬精度的前提下，完成對圓柱形研磨介質運動行為的預測。材料參數如表 2 所列。

表2 材料參數Tab.2 Parameters of material

3 結果分析

3.1 模型驗證

選取 Bian 等人[23]的試驗來驗證自行開發的球磨機 DEM 模型，試驗選取了 4 種不同尺寸的鋼球，具體數量及配比如表 3 所列。從 DEM 模擬中可以獲取球磨機的功率，并將模擬結果與試驗結果做比較，如圖 2 所示。由圖 2 可以看出，除了球磨機轉速為臨界轉速的 90% 以外，其余 3 種情況的模擬與試驗結果基本吻合，因此，可以說筆者選取的模擬方法具有相當高的精度。另外，為了保證模擬精度，在后面的研究中盡量避免球磨機在超過 90% 臨界轉速條件下工作。

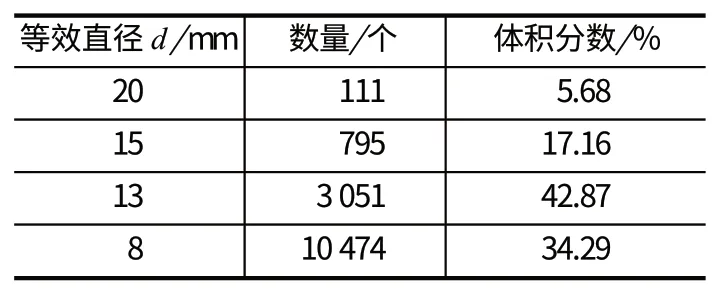
表3 球形研磨介質粒度分布[23]Tab.3 Size distribution of spherical grinding media

3.2 研磨介質的運動特性

為了研究球磨機內球形研磨介質和圓柱形研磨介質的運動特性，采取 Owen 等人[24]所選用的命名法，對 4 種關鍵位置給出定義，如圖 3 所示。

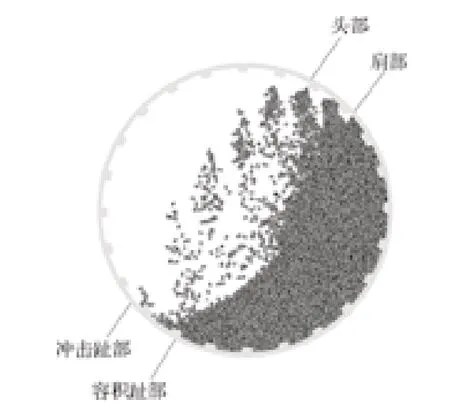
圖3 球磨機內研磨介質關鍵位置的定義Fig.3 Definition of key location of grinding media in ball mill

(1) 頭部 研磨介質與襯板接觸的最高位置稱為頭部，該位置是物料流離開襯板的最高點，也就是物料瀑流區域的頂部。

(2) 肩部 連續流動的研磨介質的頂部稱為肩部區域，該區域的研磨介質向下流向趾部區域。

(3) 沖擊趾部 研磨介質直接撞擊襯板的區域最高點稱為沖擊趾部。

(4) 容積趾部 連續流動的研磨介質的末端區域稱為容積趾部，該區域中的磨介運動方向改變并隨襯板移動。

選擇等效直徑為 8 mm 的球形和圓柱形研磨介質進行模擬，從模擬結果得出 3 種圓柱形研磨介質的分布并沒有顯著差別，因此僅選用一種圓柱形研磨介質(s1=20，s2=2) 與球形研磨介質進行比較。將位置量化為由 12 點鐘方向順時針掃過的角度，可以反映出不同研磨介質在球磨機穩定工況下的分布差異，模擬結果如圖 4 所示。顯然，球形和圓柱形研磨介質的頭部和肩部位置的垂直高度都隨著球磨機轉速的增加而增加。另外，在相同轉速下，圓柱形研磨介質具有比球形研磨介質更高的頭部和肩部位置，也就是說圓柱形研磨介質更容易被提升到一個較高位置。就沖擊趾部的位置而言，相同轉速下圓柱形研磨介質也具有比球形研磨介質更高的垂直高度。另外，2 種研磨介質容積趾部的垂直高度隨著球磨機轉速的增加而降低，相同轉速下，圓柱形研磨介質具有比球形研磨介質更低的容積趾部位置。

圖4 球磨機內球形和圓柱形研磨介質在不同轉速下的關鍵位置角度Fig.4 Angle of key location of spherical and cylindrical grinding media in ball mill at various rotary velocity

當球磨機旋轉時，研磨介質從滾筒底部移動到肩部位置，隨后開始滑動，在重力作用下在自由表面滑動到趾部位置從而完成循環。根據 Ma 和 Zhao[25]之前的研究，圓柱形顆粒之間的互鎖作用對顆粒的運動有著重要的影響。在球磨機中互鎖現象依然存在，它限制了堆疊的圓柱形研磨介質彼此之間的滑動。因此相對于球形研磨介質，肩部位置的圓柱形研磨介質更加難以滑動。在容積趾部同樣如此，圓柱形研磨介質更難以分散在球磨機的底部，這使得大多數堆疊的圓柱形研磨介質 (即類似于腎臟形狀的部位) 的流動間歇性較高。

根據之前的研究結果[24]，球磨機的工作條件 (如轉速、填充率和提升條形狀等) 對研磨介質運動行為有著顯著的影響。在本研究中，由于提升條高度及研磨介質填充率等參數保持恒定，因此研磨介質的運動行為差異主要受球磨機的轉速以及研磨介質的形狀所影響。為了更直觀地觀察穩定狀態下研磨介質運動狀態的差異，截取球磨機在 33.45 (ψ=60%) 和 44.60 r/min (ψ=80%) 2 種轉速下的研磨介質的運動瞬態圖，如圖 5 所示。

從圖 5 可以看到，邊緣較為光滑的圓柱形研磨介質 (s1=4) 比其他 2 種棱角更加尖銳的圓柱形研磨介質 (s1=8 和s1=20) 更接近于球形研磨介質 (s1=2)，且隨著s1的增加，研磨介質在磨機中的分布變得更加密集。如前文所述，在相同的球磨機轉速下，圓柱形研磨介質具有較高的肩部和頭部位置，以及比球形研磨介質更低的容積趾部位置 (即圓柱形研磨介質的瀑流彈道軌跡更高)。為了探究原因，截取轉速為44.60 r/min (ψ=80%) 時球磨機頭部位置的球形和圓柱形研磨介質的瞬態圖，如圖 6 所示。

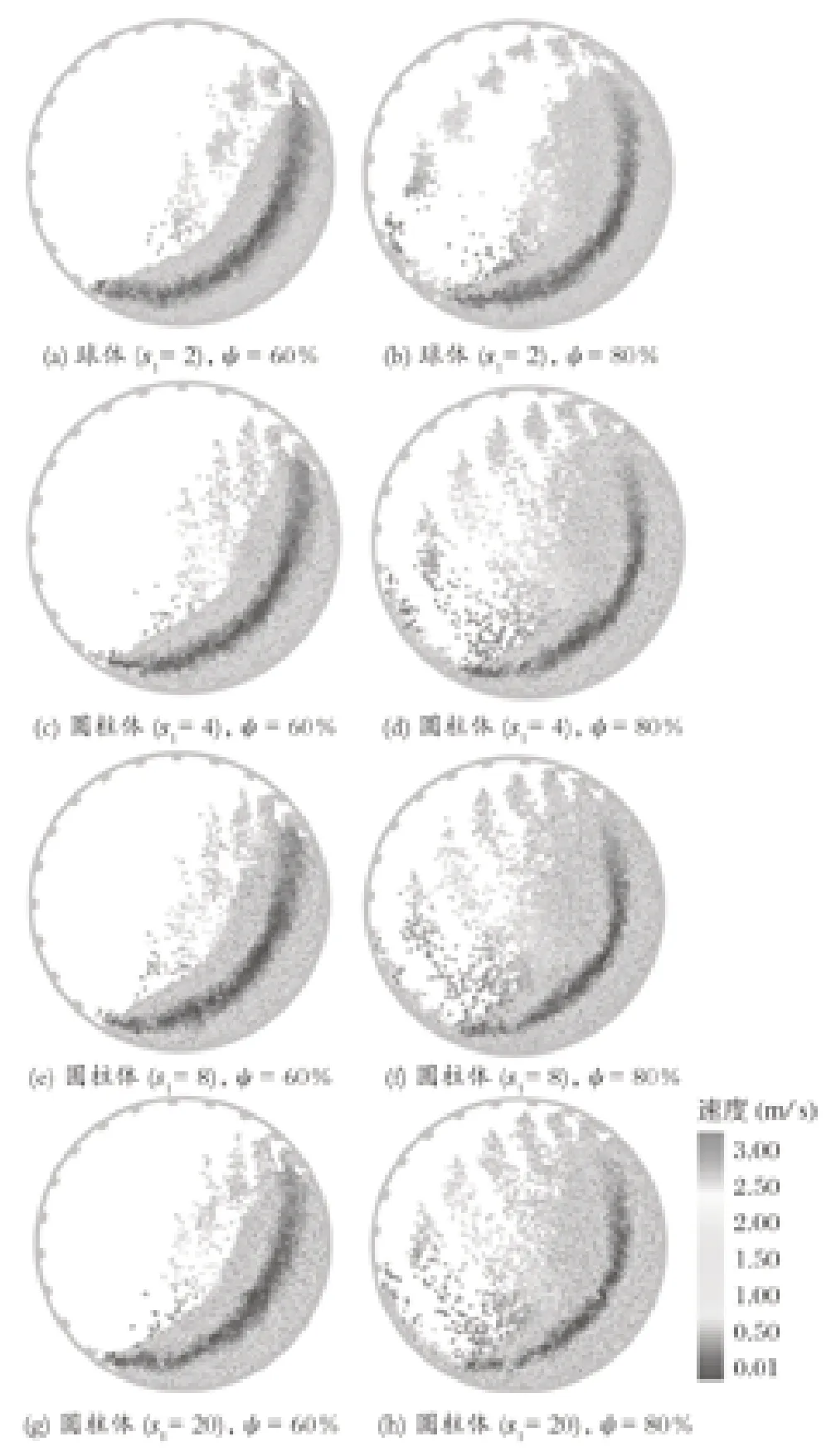
圖5 不同轉速下研磨介質的運動狀態Fig.5 Motion state of grinding media at various rotary velocity

圖6 球磨機頭部位置的球形和圓柱形研磨介質瞬態圖Fig.6 Transient state of spherical and cylindrical grinding media at toe of ball mill

顯然，在球磨機頂部的圓柱形研磨介質分布比球形更加密集，這意味著更多的圓柱形介質可以通過提升條提升到球磨機的頂部，并且球形研磨介質相對于圓柱形研磨介質更容易從提升條滑落或滾落。從圖 6可以發現，當研磨介質即將離開提升條時，圓柱形研磨介質的母線或兩個端面更傾向于緊貼在提升條上，這導致圓柱形研磨介質和提升條之間存在更嚴重的滑動摩擦，使得圓柱形研磨介質相對于球形研磨介質更難以在低位脫離提升條。因此，提升條會在高位拋出更多的圓柱形研磨介質，這種現象在球磨機轉速較高的情況下尤其明顯。

3.3 功率損耗

為了研究研磨介質的形狀和尺寸對球磨機功率的影響，對上述 4 種等效直徑為 8、13、15 和 20 mm 的研磨介質進行模擬。圖 7 顯示了球磨機不同轉速下 4種研磨介質的功率。

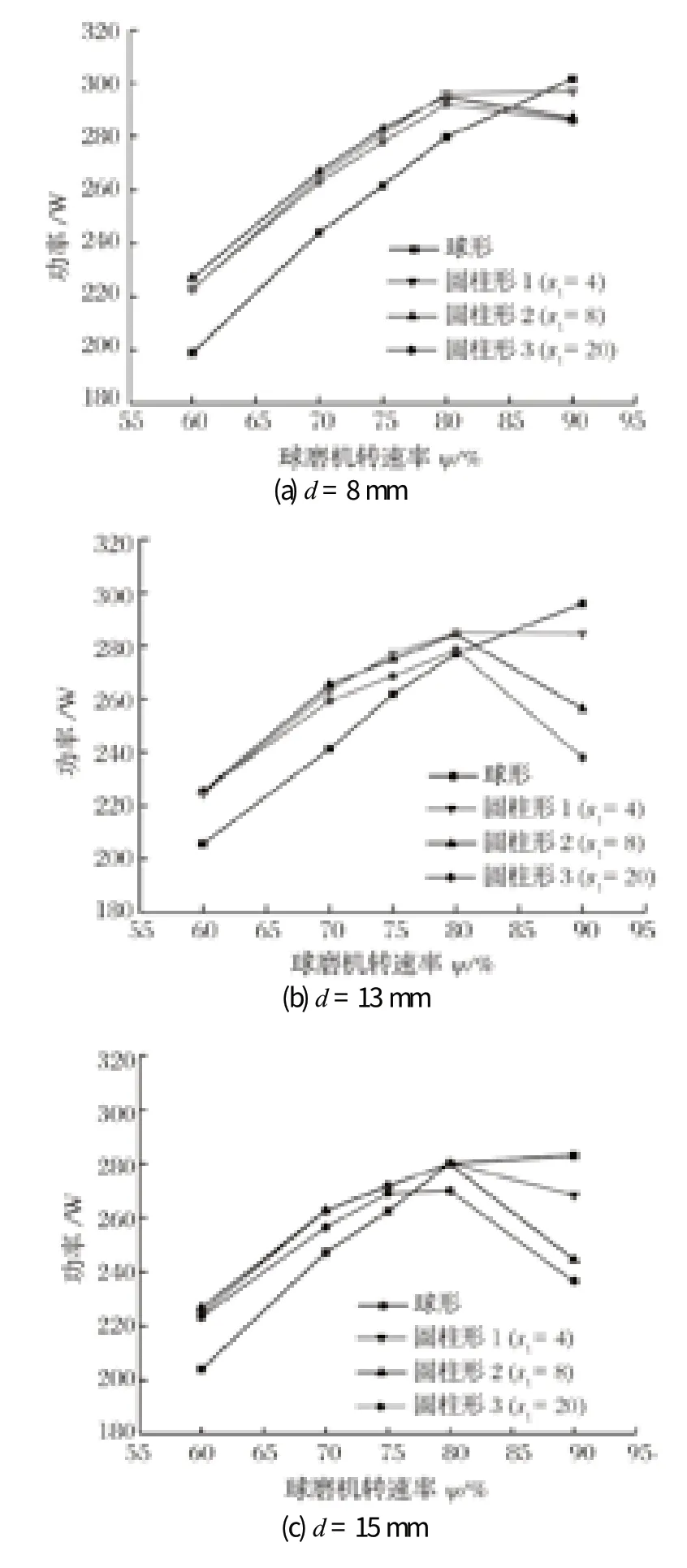
圖7 不同轉速下 4 種研磨介質的球磨機功率比較Fig.7 Comparison of power of ball mill containing four kinds of grinding media at various rotary velocity

從圖 7 可以觀察到，球形研磨介質除直徑為 20 mm 的情況外，功率通常隨著轉速的增加而增加，而圓柱形研磨介質的功率在達到峰值后下降。當球磨機的轉速低于 44.60 r/min (ψ=80%) 時，圓柱形研磨介質在相同轉速下的功率消耗明顯高于球形。隨著球磨機轉速的進一步增加，圓柱形研磨介質的離心運動越來越明顯，從而導致功率下降。而當研磨介質的尺寸增加時，這種現象更加明顯。如前文所述，這是由于圓柱形研磨介質與提升條之間存在更多的線接觸和面接觸，從而產生了更大的滑動摩擦力，使得圓柱形研磨介質更容易被提升器提升，所以當球磨機的轉速較高時更容易離心，這導致裝有圓柱形研磨介質的球磨機的功率低于球形研磨介質。當研磨介質的尺寸增加時，所有研磨介質都更容易離心，因此功耗大大降低。

3.4 碰撞能量

圖8 顯示了轉速為 33.45 r/min (ψ=60%) 時研磨介質之間的碰撞頻率和能量耗散率曲線。從圖 8 可以明顯看出，由于相似的形狀，s1=8 和s1=20 這 2 種圓柱形研磨介質的碰撞頻率和能量耗散率曲線幾乎重合。與這 2 種圓柱形研磨介質相比，在碰撞能量小于6×10-6J 時，球形和另一種圓柱形研磨介質 (s1=4)的碰撞頻率和能量耗散率曲線較低，特別是球形研磨介質的曲線明顯低于其他形狀的介質。隨著碰撞能量的增加，在能量介于 6×10-6～2×10-4J 之間時，球形研磨介質的曲線大幅增加，超過了其他 3 條曲線；隨著能量進一步增加，碰撞頻率和能量耗散率達到最大值后逐漸減小，球形研磨介質的曲線下降得更快，并且明顯低于其他研磨介質的曲線。基于以上分析可以得出結論：在較低轉速 (ψ=60%) 時，球形研磨介質的碰撞頻率和能量耗散率的分布與圓柱形研磨介質相比較窄，碰撞的能量范圍更加集中。

在轉速為 44.60 r/min (ψ=80%) 時，研磨介質之間的碰撞頻率和能量耗散率曲線如圖 9 所示。與低轉速 (ψ=60%) 情況相比，球形研磨介質的曲線沒有明顯變化，然而圓柱形研磨介質的碰撞頻率和能量耗散率的分布變得更加均勻，最大值明顯低于球形研磨介質。其原因可能是圓柱形研磨介質相對于球形被拋在空中的數量較多，使得圓柱體之間的碰撞比球體之間的碰撞更加復雜。

3.5 襯板磨損

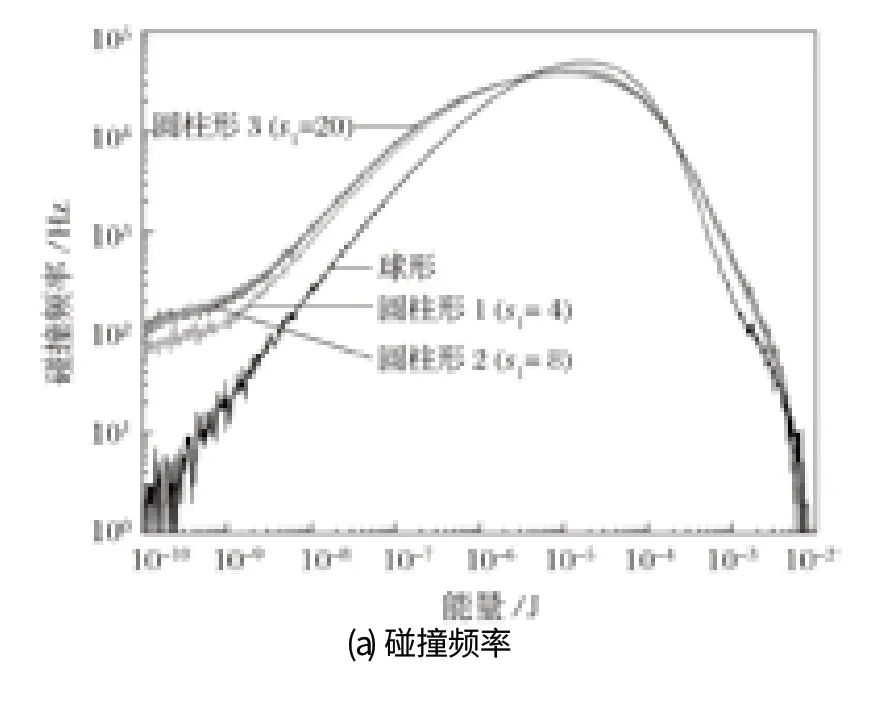
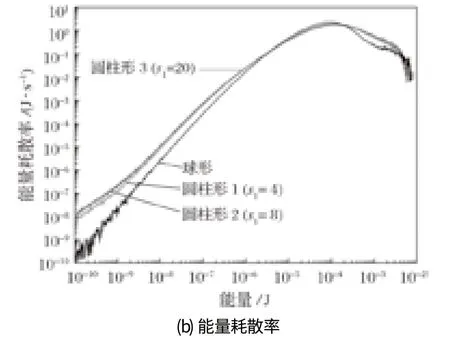
圖9 轉速為 44.60 r/min (ψ=80%) 時研磨介質間的碰撞頻率和能量耗散率曲線Fig.9 Curve of impact frequency and energy dissipation rate of grinding media at rotary velocity being 44.60 r/min (ψ=80%)

襯板磨損問題是球磨機應用中的常見問題。在相同的工作條件下，選擇球形和圓柱形研磨介質 (s1=20) 來探索研磨介質形狀對襯板磨損的影響。對 2 種研磨介質在球磨機穩定狀態下旋轉一圈所造成的襯板磨損量進行對比，結果如圖 10 所示。顯然，研磨介質對襯板的磨損量隨著球磨機轉速的增加而增加。與球形研磨介質相比，相同轉速下圓柱形研磨介質對襯板的磨損更加嚴重。經分析認為是由于以下兩個原因：首先，與同一轉速下的球形研磨介質相比，提升條會拋出更多高速運動的圓柱形研磨介質，直接撞擊襯板造成極大的磨損，這也解釋了轉速越高兩者差值越大的原因；其次，在圓柱形研磨介質和襯板之間存在更多的滑動，導致更多的滑動摩擦力做功，使得磨損現象更加明顯。

圖10 不同轉速下 2 種研磨介質對球磨機襯板的磨損量比較Fig.10 Comparison of liner wear amount of ball mill containing two kinds of grinding

4 結論

基于超橢球模型并利用離散單元法研究了 4 種不同形狀研磨介質對球磨機內物料運動行為的影響，主要可以得到以下結論：

(1) 在研磨介質運動特性方面，在相同的工作條件下，相對于球形研磨介質，圓柱形研磨介質的頭部、肩部以及沖擊趾部垂直高度較高，容積趾部高度較低。

(2) 在功率損耗方面，在相同的工作條件下，圓柱形研磨介質的功率一般高于球形研磨介質，但在球磨機高轉速條件下，由于圓柱形研磨介質存在更明顯的離心運動，會使得功率顯著下降。

(3) 在碰撞能量方面，在較低轉速 (ψ=60%) 條件下，圓柱形研磨介質之間的碰撞頻率和能量耗散率分布得更為均勻，當轉速較高 (ψ=80%) 時，這種現象更加明顯。

(4) 在設備磨損方面，在相同的工作條件下，圓柱形研磨介質對襯板的磨損大于球形研磨介質。