基于改進的SURF 算子和透視變換模型的圖像配準*

徐 明 刁 燕 羅 華 黎 彪

（四川大學機械工程學院 成都 610065）

1 引言

21 世紀以來，由于科技的進步，計算機進入大眾的視野以及計算機技術得到飛快的發展，圖像處理技術也得到前所未有的飛躍，圖像配準作為圖像處理的重要組成部分已經廣泛應用于模式識別、醫學圖像處理、計算機視覺等領域［1～3］。

目前研究的圖像配準方法中，主要可以分為兩大類：一類是基于灰度的配準方法，另一類是基于特征的配準方法［4～5］。第一種是基于灰度的圖像配準方法，比較簡單，也容易理解，主要是通過兩幅圖像的灰度值的變化來進行匹配，但是此方法穩定性差，匹配精度低；相比之下，第二種是基于特征的匹配方法，具有很好的穩定性和魯棒性，對光照、旋轉、尺度等變化有很好的不變性，是當前圖像配準方法中最流行的方法［6］。

學者們在進行圖像配準的過程中，為了提高配準的精度，他們對圖像的特征點［7］、特征輪廓［8］進行研究。2004 年，Lowe 完善了尺度不變特征（Scale Invariant Feature Transform，SIFT）算法［9］，通過建立尺度空間、構建圖像金字塔、生成特征描述子來尋找圖像的穩定特征點，雖然這種方法有良好的穩定性，但是SIFT 算法復雜度高、耗時長、計算量大，匹配效率低。2006年，Bay對SIFT算法進行了改進——加速魯棒特征（Speeded Up Robust Feature，SURF）算法［10］，該方法具有很好的魯棒性，相對SIFT 算法速度提高了3 倍，但對于圖像旋轉和尺度變換過大時，依然存在誤匹配，使得匹配精度低。

針對上述方法的優點以及方法存在的不足，本文提出了一種基于改進的SURF 算子和通過透視變換模型的圖像配準算法。

2 SURF算法原理

2.1 積分圖像

SURF 算法中通過利用積分圖像，圖像與高斯二階微分模板的濾波運算就可以轉換成通過對積分圖像的簡單加減，從而減少運算量，提高計算速度。因此，計算圖1 中S 區域的灰度值積分就可以通過S=A-B-C+D來求得。

圖1 積分圖像法

2.2 DoH近似

圖像I中像素點(x，y)，有尺度為σ的Hessian矩陣：

式中，Lxx(x，σ)表示圖像I(x，y)與高斯函數二階微分在點x處的卷積，同理，Lxy(x，σ)和Lyy(x，σ)也有類似的定義。

高斯函數的高階微分與離散的圖像函數I(x，y)做卷積運算時相當于高斯濾波模板對圖像做濾波處理。在實際的運用過程中，用盒子濾波運算來替代卷積運算，簡化了對高斯二階微分模板的計算。對于σ=1.2 的高斯濾波器，我們設定9×9大小模板尺寸的盒子濾波器，并用它作為最新的尺度空間值來對圖像進行濾波斑點檢測。使用Dxx、Dxy和Dyy來表示模板與圖像卷積運算后的結果，來用替代Lxy、Lxy、Lyy。如圖2所示。

因此，便可以對已得到的Hessian 矩陣的行列式進行簡化：

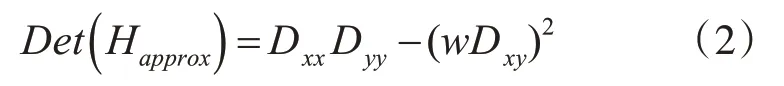
式中：Det(Happrox)表示在x點鄰域的盒子濾波響應值，主要用來檢測極值點；w是一個參數，通常取0.9。

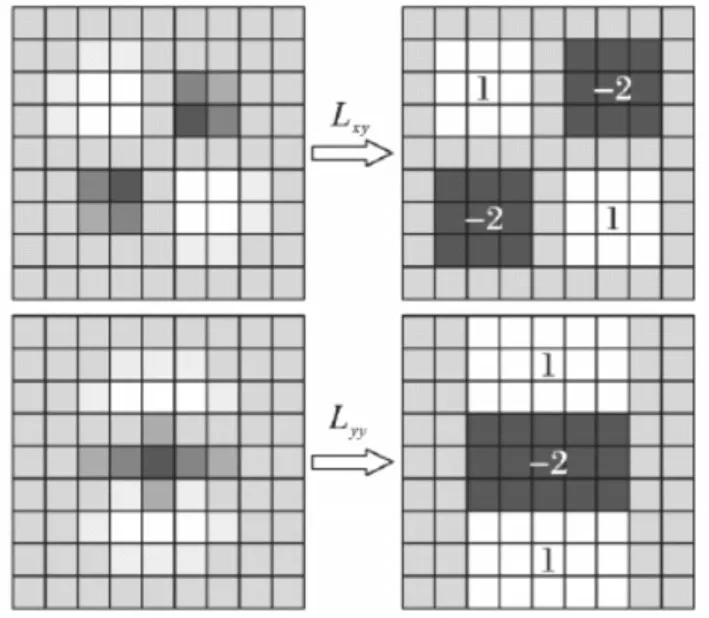
圖2 盒子濾波器

2.3 尺度空間建立

為了能夠獲得不同尺度上的斑點，必須通過建立圖像的尺度空間金字塔，如圖3所示。

圖3 圖像金字塔

建立圖像金字塔的基本思路是：保持原圖像大小不變，通過改變濾波器的大小，但要保證濾波器內核為奇數，就能夠得到不同的尺度空間。SURF算法采用不斷增大盒子模板的尺寸，利用不同尺寸的盒子濾波器模板與積分圖像得到Hessian矩陣的響應值，然后在響應圖像求得極值點，計算出不同尺度的特征點。

2.4 特征點定位

為了在不同尺度空間定位出特征點，需要在響應圖像上進行3×3×3 鄰域的非極大值抑制，使同尺度中相鄰的8個像素點與其上下相鄰尺度的各9個像素點相比較，如圖4所示。

圖4 非極大值抑制

在進行極值比較的過程中，如果該極值大于或小于相鄰26 個點的極值，則該點保留下來，作為初步的特征點。然后通過擬合三維二次函數對興趣點進行定位，使其達到亞像素級，從而獲得穩定的特征點。

2.5 確定特征點主方向

由于關鍵點鄰域像素的梯度方向是不同的，為了使目標圖像具備旋轉不變形，就要為每一個興趣點指點一個確定的方向，確定特征點主方向。首先以上述得到的特征點為中心，在半徑為6s的鄰域中計算x和y方向上的Harr小波響應，小波的邊長為4s，計算半徑為6s（s為特征點所在的尺度值）鄰域內的點分別在x，y方向上的Harr 小波響應，Harr 小波邊長取4s，并對響應值進行高斯加權。然后，在60°的扇形區域內由相應的高斯加權權重得到新的矢量，選擇最長的矢量為該特征點的主方向，如圖5所示。

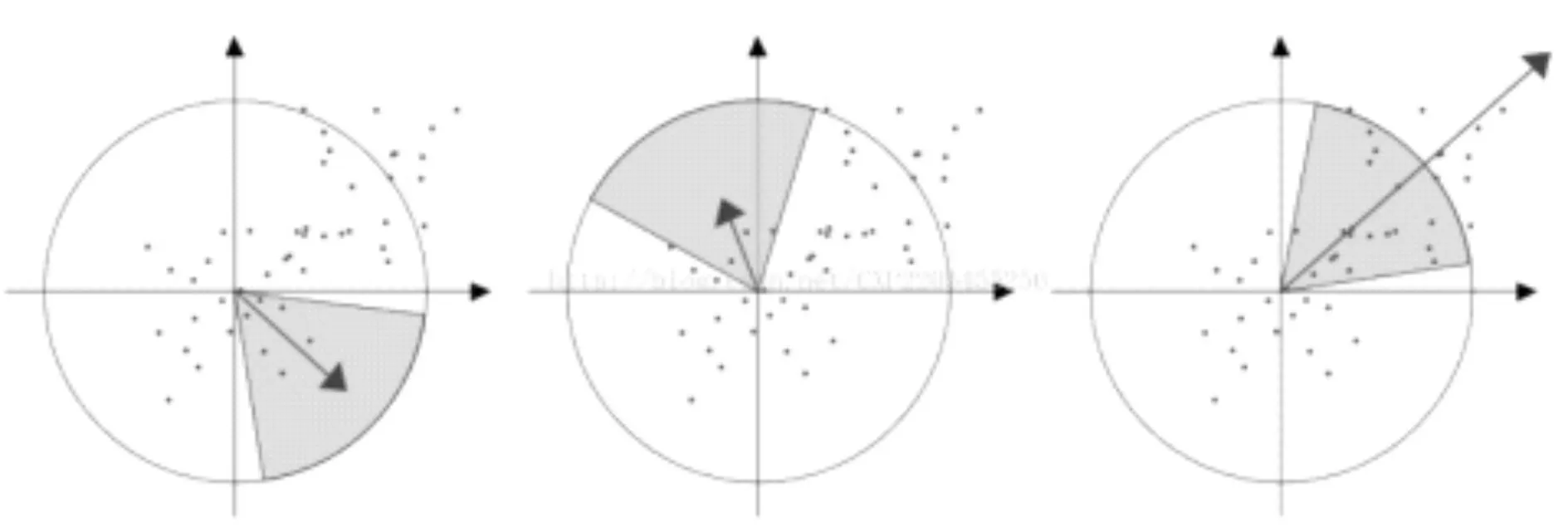
圖5 選取特征點的主方向

2.6 生成描述子

上述的操作已經知道了特征點的位置以及特征點的主方向，接下來就是要在局部區域內計算出特征描述子。首先根據特征點的主方向調整坐標系使其方向一致，以保證旋轉不變性。再以特征點為中心，在特征點周圍選取一個鄰域為20s×20s的正方形框，把它劃分為4×4 個子區域，然后用尺寸寬度為2s的Harr小波模板對每個子區域進行響應值計算，得到每個子區域的響應信息。由于每個子區域攜帶4 個信息，所以得到的特征描述子由4×4×4=64 維特征矢量構成。

3 結合改進的SURF 算子及其配準過程

3.1 改進的SURF特征描述符

SURF 算法在對彩色圖像配準中，首先要將彩色圖像處理成灰度圖像，并且只用到了彩色圖像的亮度信息，并不能充分利用彩色圖像的色彩信息，因此在配準過程中會丟失相關的信息，從而降低了彩色圖像的配準率。本文將只含有灰度信息的SURF 特征描述符增加了圖像的色彩信息，形成改進的SURF特征描述符。

通過對SURF 特征點以及特征點鄰域內RGB的顏色信息進行分析，可以在SURF 特征描述符的基礎上增加RGB 色彩分量描述符來描述特征點的色彩信息，步驟如下。

假定SURF特征點在(x，y)處RGB 三通道的值分別為r、g和b，且r，g，b?[0，255]，SURF特征點和特征點鄰域內像素點的總數為n。

S1：在RGB 彩色空間中，分別計算出圖像特征點以及特征點鄰域內所有像素點的每個通道的均值μr、μg、μb。

將μr、μg、μb三個值組成一個包含RGB 色彩均值的三維向量E=(μr，μg，μb)。

S2：在RGB彩色空間中，分別計算圖像特征點以及特征點鄰域內所有像素點的每個通道的方差δr、δg和δb。

將δr、δg和δb三個值組成一個包含RGB色彩方差的三維向量S=(δr，δg，δb)。

S3：將E和S分別歸一化處理，得到三維RGB色彩均值向量En和三維RGB色彩方差向量Sn。

S4：將En與Sn合并，構成了一個包含了色彩信息的六維RGB色彩分量描述向量Vc。

S5：在特征點鄰域4×4 的子區域范圍內，將原有的 SURF 特征描述向量Vs=(i1，i2，…，i64)上疊加六維RGB 色彩分量描述向量Vc，組成改進的且包含色彩信息的70維SURF特征描述向量。

3.2 FLANN算法進行特征點匹配

FLANN 算法是 Muja 和 Lowe［11～12］于 2009 年 提出的，主要是基于K 均值樹或KD-TREE 操作實現的，根據數據集的分布特點和空間資源消耗的要求來推薦搜索類型和檢索參數。FLANN 算法模型的特征空間一般是n 維實數向量空間Rn，該算法的核心是通過歐式距離來尋找與實例點最鄰近的點，歐氏距離的定義如式（8）所示。

如果D 值越小，就表示這些特征點對之間的距離越“近”，也就說明了這些特征點相似程度越高。

本文通過KD-TREE 方法將數據點在n 維空間Rn劃為幾個特定的部分，其作用主要是在KD-TREE中檢索與查詢點距離最近的歐式距離［13］。

在向量空間Rn中，通過KD-TREE結構將所有的歐氏距離存儲，就能夠更有效查詢與參考點最相近的點。KD-TREE的整個搜索過程是從上而下的一個遞歸的過程。首先是以特定的基準將目標點和分割點分開，然后進行比較，再判斷目標點是在左邊的區域還是右邊的區域；一直循環與對應點進行比較，直到目標搜索成功。

3.3 RANSAC算法特征點篩選

由FLANN 算法通過初步匹配得到的特征點中還存在大量匹配錯誤的特征點，為了減少誤匹配點，保證配準的準確性，需要采用隨機采樣一致性算法（Random Sample Consensus，RANSAC）對特征點 進 行 篩 選 。RANSAC 是 Fischler 和 Bolles［14］在1981 年最先提出，是目前剔除錯誤匹配點方法中最廣泛使用的一種。使用RANSAC 方法的流程如下所示。

Step1：在初步匹配集P中隨機抽出4 組特征點對（要求4 個特征點不共線），計算出變換矩陣H，記為模型M；

Step2：計算P中所有數據與模型M的投影誤差，如果誤差小于閾值t，就將誤差加入內點集I，并且記錄此模型下的統計誤差；

Step3：對上述步驟進行重復，當計算得到新的模型，比較其統計誤差error與errormin大小，如果error更小，就需要更新模型M和errormin。

Step4：計算出最優模型M和最大內點集I。

在步驟1 中，取4 組特征點對是因為本文選擇的幾何變換模型是透視變換模型，該模型中有8 個未知的參數，至少需要8 個方程來對其進行求解，一組特征點對可以列出兩個方程，因此需要選擇4組特征點對。

3.4 透視變換

由匹配點來對源圖像和目標圖像之間進行坐標轉換，可以得出兩幅圖像的關系，即透視變換矩陣H，如下所示。

若p=(u，v) ，q=(x，y) 為一對匹配的特征點對，則投影變換公式為

其中，(u，v)為源圖像中的坐標，為變換之后的目標圖像的坐標，由得到的最優模型M可計算出H中的各參數hi(i=0，1，2，…，7)，再通過透視變換就可以完成源圖像到目標圖像之間的配準。

4 實驗結果與分析

針對本文提出的改進SURF 算法，通過Mikolajazyk［15］數據集對本算法進行驗證。分別從圖像的光照變化、平移與模糊變化、旋轉與尺度變化和視角變化四組情況下驗證本文算法與SURF 算法的匹配性能。

4.1 運行環境

實驗條件是在硬件條件為Intel 酷睿i7-7200U CPU @3.5GHz、8G內存、64位操作系統的Windows10 PC 機上處理數據，其應用的軟件為VS2015，開源計算機視覺庫OpenCV3.4。

4.2 配準實驗結果及分析

1）第一組是在光照變化下對圖像的測試，通過改變圖像的光照情況，圖6（a）為原始輸入圖像，左圖為測試圖像，右圖為基準圖像。圖6（b）和圖6（c）分別是用SURF 算法和本文算法來對兩幅圖像進行角點匹配，再利用本文算法得到的精確匹配點計算出單應矩陣：

通過得到的單應矩陣H可以實現對圖像的精確配準，如圖6（d）所示。

圖6 光照變化圖像配準

2）第二組是在平移和模糊變化下對圖像的測試，圖7（a）為原始輸入圖像，左圖為測試圖像，右圖為基準圖像。圖7（b）和圖7（c）分別是用SURF 算法和本文算法來對兩幅圖像進行角點匹配，再利用本文算法得到的精確匹配點計算出單應矩陣：

通過得到的單應矩陣H可以實現對圖像的精確配準，如圖7（d）所示。

圖7 平移與模糊變化圖像配準

3）第三組是在大角度旋轉和尺度變化下對圖像的測試，通過對圖像進行旋轉和尺度變化的情況，圖8（a）為原始輸入圖像，左圖為測試圖像，右圖為基準圖像。圖8（b）和圖8（c）分別是用SURF 算法和本文算法來對兩幅圖像進行角點匹配，再利用本文算法得到的精確匹配點計算出單應矩陣：

通過得到的單應矩陣H可以實現對圖像的精確配準，如圖8（d）所示。

圖8 旋轉與尺度變化圖像配準

4）第四組是在視角變化下對圖像的測試，圖9（a）為原始輸入圖像，左圖為測試圖像，右圖為基準圖像。圖9（b）和圖9（c）分別是用SURF 算法和本文算法來對兩幅圖像進行角點匹配，再利用本文算法得到的精確匹配點計算出單應矩陣：

通過得到的單應矩陣H可以實現對圖像的精確配準，如圖9（d）所示。

圖9 視角變化圖像配準

本文實驗是在相同條件下對SURF 算法和本文所優化的算法從匹配的準確性進行比較。從表1 中可以看出：對同一對測試圖像來說，SURF 檢測的特征點總點數要多于本文優化算法的特征點數，但匹配的精度低于本文優化算法的精度。所以從表中可以反映出，本文提出的方法對光照、平移和模糊、旋轉和尺度、視角變化在匹配正確性以及匹配精度方面性能更優。

表1 四組圖像匹配結果對比

5 結語

針對圖像的匹配性能差以及誤匹配率高，提出了一種基于改進的SURF 算子和通過透視變換模型的圖像配準算法，通過和SURF 算法進行對比，提高了圖像的匹配精度，并利用單應矩陣實現圖像配準。由于圖像配準可以應用于圖像識別，計算機視覺等熱門領域，所以在后續的研究中，希望能提高圖像匹配的效率，獲得更加穩定的圖像特征匹配。