云計算中基于遺傳算法的數據布局策略*

覃偉榮

（欽州學院資源與環境學院 欽州 535011）

1 引言

隨著計算機業務應用程序的不斷發展，數據量正在呈指數級增長，網絡設備的增加和互聯網的發展，使得數據的生成和存儲容量爆炸式增長，數據中心面臨著龐大的訪問量［1］。傳統的數據庫管理無法滿足數據的龐大和數據結構的復雜，進而難以實現數據存儲和管理要求。分布式云計算系統架構可以為計算資源提供更高的性能，并且優化海量存儲資源。然而，在分布式云計算系統中，數據密集型計算需要處理大量的數據，在多數據中心環境中，某些數據必須放在指定的數據中心內且不能傳輸［2］。云計算處理不可避免的引起數據中心之間的數據調度，由于數據量巨大且網絡帶寬有限，數據中心之間的數據調度已成為網絡傳輸中的巨大問題［3］。

關于分布式系統中的數據布局已有很多研究［4～6］，通常可以分為兩種類型：靜態數據布局［7］和動態數據布局［8］。大多數靜態數據布局算法需要完全掌握網絡環境負載信息，例如所有文件的存儲時間和訪問速率［9］。動態數據布局算法在線生成文件磁盤分配方案，并以此適應不同的網絡負載模式，進而不必對分配文件進行先驗處理。動態數據布局策略在每個請求上更新布局策略，當數據量相對較小時，Web代理緩存才會有效［10］。文獻［11］基于數據相關性建立數據布局策略，但數據相關性的定義并不滿足數據布局，且沒有提出有效的方法來減少數據中心之間的數據調度量。

為了滿足分布式云計算中數據布局的合理性，本文利用遺傳算法合理布局數據策略。通過數據中心之間的數據調度建立分布式云計算的數學模型，結合適應度函數的倒數建立目標函數來評估每個個體的適合度。在初始種群按照優勝劣汰的原則生成后，每一代的進化產生更好的近似解，運用輪盤賭法則選擇具有高適合度值的適當個體，并且消除具有低適應值的個體。通過遺傳算法的交叉和變異操作改變數據集的布局位置。最終在在優勝劣汰的原則下找到最優個體。

2 云計算中的數據調度模型

在云計算系統中，數據存儲通常達到PB 級規模，復雜多樣的數據結構對數據服務類型和高級別要求的數據管理帶來了巨大壓力［12］。本文以數據中心之間的數據調度模型為基礎，并建立精確數據布局的理論基礎。

假設云計算系統具有l個數據中心，依據數據中心固有屬性劃分為N個不同的數據集。根據用戶請求數據資源，將數據集不同的操作分配到M個計算中。數據調度的模型，如圖1所示。

圖1 數據中心之間數據調度的物理模型

假設云計算系統中的數據集合為

其中，n是數據集的數量，數據集di的大小為εi。

系統中的l個數據中心表示為

系統中的m個計算表示為

每次計算的執行頻率可表示為

其中，μi是單位間隔內計算ci的執行頻率。

本文定義一個處理因子αij，其中

因此，可以得到計算集C和數據集D的關聯矩陣表示為

在本文中，數據副本不在考慮之列。同樣，本文定義了一個布局因子βjk，其中

由數據集D和數據中心S之間的關聯矩陣（布局矩陣）可以表示為

關聯矩陣（布局矩陣）B用于表示數據中心S中存儲數據集D的狀態。其中，依據權重原則矩陣B中每行的元素之和為1：

其中，第k列的元素總和是數據中心Sk中存儲數據集的數量，當數據集放入數據中心Sk時，存儲的數據應滿足Sk的基本容量，則

定義矩陣Z表示為

假設

則矩陣Z=[zik]m×l，zik是數據中心一次計算ci時處理的數據集的數量。每個列中的元素的總和表示為，它是在所有的計算被執行一次時在數據中心Sk中處理的數據集的數目。定義一個函數u(zik)表示為

計算ci執行過程中訪問的數據中心數量為計算c執行一次的數據調度次數為i當布局矩陣為B時，在單位區間內系統中所有計算的執行期間的數據調度總數可以表示為

本文的目標是找到最佳的數據布局解決方案B*最小化Γ(B)：

3 遺傳算法

3.1 算法選擇

在大數據布局問題中，由于B矩陣稀疏分布，則解空間非常龐大。傳統的優化算法有窮舉搜索算法、蒙特卡洛算法、遺傳算法、模擬退火算法等。

窮舉搜索算法［13］是搜索最優布局矩陣的直接方法。它計算出所有可能的數據布局B矩陣，然后遍歷找到最小的Γ(B) ，此時布局矩陣是最優解。然而窮舉搜索算法的計算復雜度很高，近似于(ln)。在分布式云計算系統中，數據集n的數量使得計算復雜度對系統求解更加困難。此外，還存在一些約束條件，如存儲容量限制和無副本限制使得布局問題成為NP 難問題。因此，只有當數據集的數量很小時，才能使用窮舉搜索算法。

蒙特卡洛算法［14］利用概率論和統計方法。在數據布局中，通過隨機生成一定數量的B矩陣作為樣本，計算每個樣本矩陣B上的數據中心之間的數據調度，并找出具有最小數據調度的布局矩陣。與窮舉搜索算法相比，蒙特卡洛算法的計算復雜度有所提高，但B矩陣在解空間中稀疏分布，蒙特卡洛算法的搜索效率仍然不高。它在生成布局矩陣時具有很強的規律性和約束條件。

遺傳算法通過問題狀態空間進行定向搜索，其比隨機搜索算法［15］、枚舉法［16］或演算進化算法［17］更加有效。因此，利用遺傳算法可以解決大數據中的數據布局問題。

3.2 算法應用

遺傳算法針對優化問題的候選解決方案群體（稱為個體），每個個體適應環境的程度由適應度來表示，在每一代中，對種群中每個個體的適應值進行評估，從當前種群中隨機選擇具有較高適應值的個體，然后進行交叉和變異算子操作來形成新一代，最后在算法的下一次迭代中使用新一代候選解決方案［18］。

1）編碼

數據中心的數據集由矩陣B表示可以表示遺傳算法的數據布局，結合矩陣的字符串結構直接將布局矩陣作為基因型進行編碼。

2）個體和種群

個體作為種群搜索空間中的點，數據布局的搜索空間由布局矩陣的集合組成。種群構成整個搜索空間的子集。

3）適應度函數

適應度函數在遺傳算法的數據布局問題中，目標函數 Γ(B) 可以作為目標函數的倒數，即F=1/Γ(B)。

4）遺傳算子

（1）選擇：輪盤賭選擇是遺傳算法中用于選擇潛在重組方案的遺傳算子，更高的適合度的染色體更容易被選擇。輪盤賭選擇的步驟如下：

步驟1：在種群中獲得N個個體的適應度值f(i)。

步驟2：假設存在個體k，其被選擇的概率為p(k)：

步 驟 4：生 成 隨 機 數r(0 ≤r＜1) ，如 果q(k-1)＜r＜q(k)，則選擇個體k。

（2）交叉：假設B1與B2配對，產生兩個隨機數r1、r2(0 ＜r1＜r2＜n)作為交叉點，則交換這兩個點之間的基因產生子代。在布局矩陣上進行兩點交叉算子的4×3布局矩陣，如圖2所示。

圖2 兩點交叉算子布局矩陣示意圖

（3）變異：對于二進制字符串，染色體變異一個或多個基因。如果基因組位是1，則改變為0，反之亦然。當在布局矩陣中使用變異算子時，生成隨機數r1（0 ≤r1＜n），改變數據集的位置，然后生成兩個隨機數r2、r3(0 ≤r2≠r3＜l)，如果為1，則將其從1 變為0，從 0 變為 1；如果為0，則將其從0變為1，同時將同一行中的另一個1從1更改為0，以確保每行只有一個1，從而改變數據集dr1在數據中心的布局。在布局矩陣上進行兩點交叉算子的4×3布局矩陣變異，如圖3所示。

圖3 在布局矩陣上進行變異算子

4 基于遺傳算法的數據布局過程

步驟1：根據實際情況確定人口規模（G），交叉率（Pc）和變異率（Pm）。

步驟2：生成初始種群：初始種群BG(0)由G種位矩陣組成。矩陣的所有元素都設置為0，然后生成n個隨機數 {r1，...，ri，...，rn} ，(0 ≤ri＜l)，進而生成矩陣Bi，隨機數ri表示數據集di被放入數據中心，然后布局因子從0 變為1，如果生成的矩陣不滿足式（10）中的約束條件，則放棄它并生成新的矩陣。

步驟3：計算種群BG(t)中每個個體的適合度MaxGen：通過矩陣乘法得到矩陣Z，即Z=A·B。矩陣Z中行i的非零元素的數目是計算ci期間訪問所有數據中心的次數，當計算ci執行一次時，數據調度的數量為然后，可以計算出來在單位間隔內執行系統中所有計算期間B中的數據調度總數，即：

步驟4：計算種群BG(t)中每個個體的數據調度 Γ(Bt)的數量，Bt的適應值表示為F=1/Γ(Bt)。在計算每個人的適合度值和所選擇的概率之后，通過輪盤賭從BG(t)中選擇G個個體。

步驟5：利用交叉率Pc作為交叉操作的染色體百分比，對選定的布局矩陣執行交叉算子。

步驟6：利用變異率Pm作為參與變異操作的染色體百分比，對所選擇的布局矩陣上執行變異算子。如果群體的大小是G并且每個個體具有n個基因，則待變異的基因數量為G·n·Pm。因此，可以生成隨機數r(0 ≤r≤1)，如果r＜Pm，則相應的基因將發生變異。

步驟8：根據式（7）中的布局因子βjk的定義，在找到近似最優解B*之后，數據集dj的布局可以通過B*中的布局因子βjk來確定。

5 仿真實驗

5.1 仿真環境

為了驗證本文所提出的基于遺傳算法的數據布局策略，構建了面向“Digital city”的數據存儲和訪問平臺。該平臺由20 個Dell Power Edge T410 服務器組成，每個都有8 個英特爾Intel Xeon E5606 CPU（2.13 GHz），16G DDR3 內存和 3TB SATA 磁盤組成。通過在數據中心部署獨立的Hadoop 分布式文件系統和VMware，因此將每個服務器都充當數據中心。在千兆以太網環境下，用戶可以通過Flex 4.5 開發的數字城市應用演示系統提交數據并進行計算。

5.2 仿真結果與分析

本文在數據布局中應用遺傳算法對布局策略進行綜合性能測試。為了驗證遺傳算法在數據布局中的可行性，比較了遺傳算法和窮舉搜索算法求解數據中心之間的數據調度，在數據集的數量很小時，不同數量的最小數據調度數和關系數據集之間的關系由折線圖表示。為了比較數據集數量發生變化時，不同算法搜索的數據中心之間的數據調度。通過對3個數據中心進行400次測試計算。在遺傳算法中，蒙特卡洛算法的迭代次數為106次，初始種群的規模設置為200，最大迭代次數設置為1000，交叉率和變異率分別為0.6和0.01。

數據中心之間的數據調度的算法對比，如圖4所示。從圖4 中，可以發現隨著數據集的數量變化，三種算法的結果在每種情況下都是相同的。通過遍歷得到窮舉搜索算法的結果，相應的結果是最優的數據布局矩陣，因此，利用遺傳算法和蒙特卡洛算法也可以找到最優的數據布局矩陣。

數據調度的最小次數，如圖5 所示。數據調度的最小次數隨著生成代數的增加而減小，并且優化結果更加接近最優解。其中，當數據集數量為8 個時，產生代數的收斂拐點在400。

圖4 三種算法在不同數據集的數據中心之間的數據調度

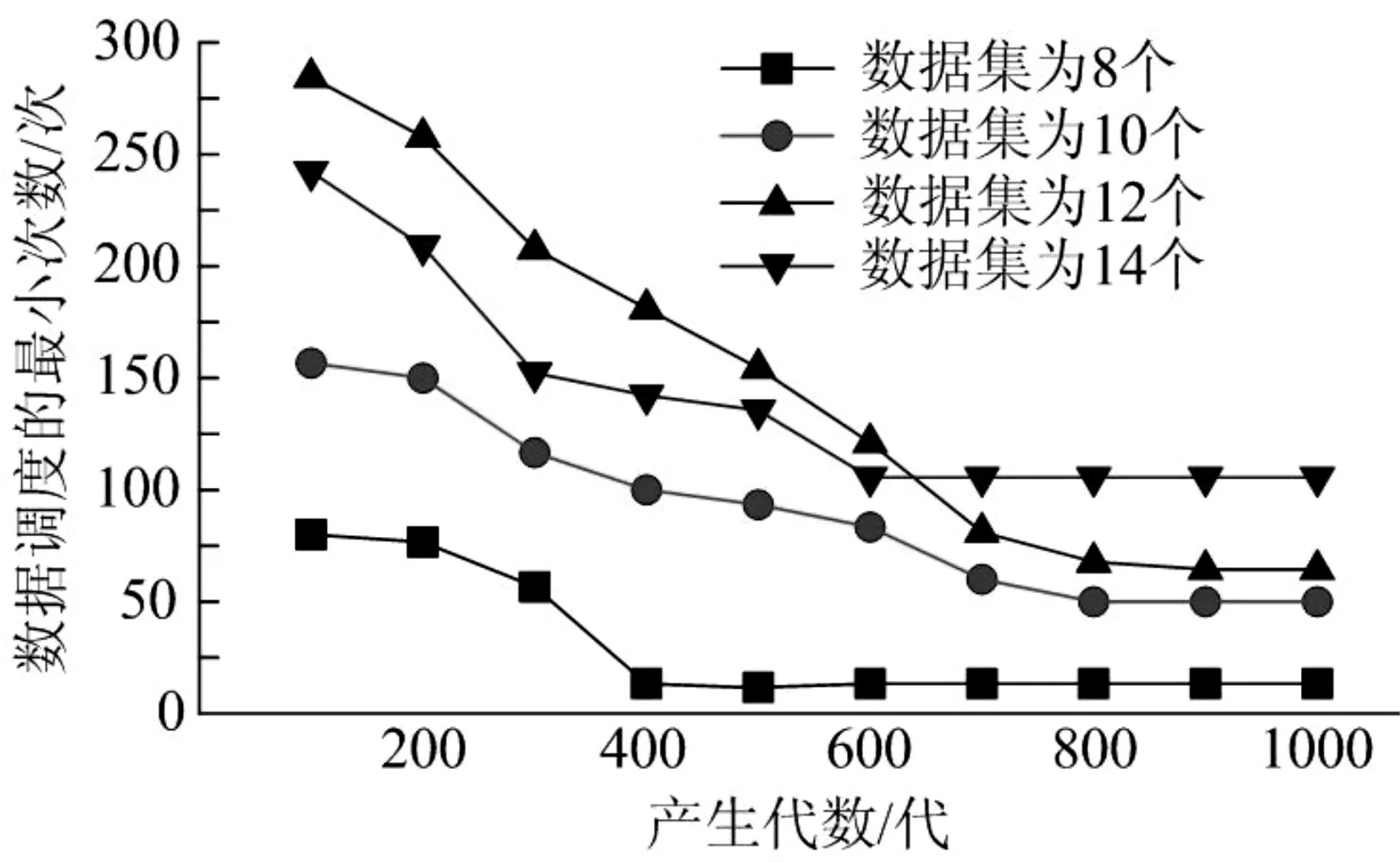
圖5 數據調度的最小次數

在數據集數量較大的情況下，將遺傳算法搜索的近似最優解數據中心的數據調度與蒙特卡羅算法搜索的結果進行了比較，并比較了各算法的優化時間。通過隨機測試計算2500 次不同數據集的數據中心。在遺傳算法中，蒙特卡洛算法的迭代次數為109次，初始種群的大小設定為5×103，最大代數設置為2000，交叉率和變異率分別為0.5和0.05。

從圖6 和圖7 中，可以看到數據集或數據中心的增加導致數據中心之間的數據調度的增長。通過對數據的比較，發現在遺傳算法中近似最優數據布局矩陣的數據中心之間的數據調度總是小于蒙特卡洛算法。因此，對于數據布局問題，在大數據集的情況下，遺傳算法的搜索結果優于蒙特卡羅算法。

圖6 不同數據集之間的數據調度

圖7 數據中心之間的數據調度

圖8 給出了不同數量的數據集的最小數據調度數與子代之間的關系。在實驗中，數據中心的數量固定為5 個。數據集的數量固定為60 時，在30個數據中心上隨機運行了2500次測試計算，如圖9所示。隨著子代的增加，數據調度次數變小，優化結果更接近最優解。

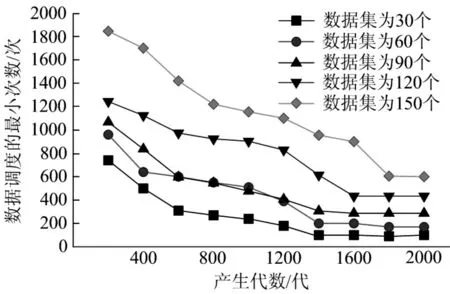
圖8 數據調度的最小次數

圖9 數據中心中數據調度的最小次數

6 結語

在分布式云計算的環境中，將數據布局到合適的數據中心已經成為一個關鍵問題。本文建立了數據集、數據中心和計算之間的數學模型。利用三種不同的算法來搜索近似最優數據布局矩陣，通過將遺傳算法與窮舉搜索算法和蒙特卡洛算法進行比較可得，遺傳算法可以找到最優的數據布局矩陣。