Meta分析模型及其應用
劉瑞銀, 暢藝婷
(沈陽師范大學 數學與系統科學學院, 沈陽 110034)
0 引 言
Meta分析是對某一特定問題的諸多研究結果進行綜合評價的一種統計方法,1976年由Glass首次命名為meta分析,并將其定義為以綜合已有的研究結果為目的,對單項研究結果進行綜合的統計學方法。Meta分析最早被應用于教育學等社會科學領域,20世紀90年代開始被廣泛應用于自然科學領域[1-6]。
假設研究的總體為X~F(x;μ,σ2),其中均值μ為感興趣的總效應量。現有K個調查小組對該問題進行調查研究,得到了K組樣本x1,x2,…,xK,其中
每一組的樣本均值記為ti,又稱作子效應量。樣本均值ti的誤差記為vi,其中i=1,2,…,K。Meta分析指的是,在不知道原始樣本x1,x2,…,xK,只知道由原始樣本估計的子效應量ti及子效應量的誤差數據vi的情況下,如何對效應量μ進行估計。
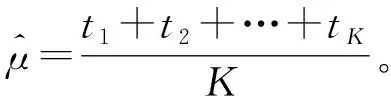
這里需要特別注意的是,研究中感興趣的效應量不一定是均值,而是根據實際情況而定的統計量。在本文中,不加注明的話,假設是均值。
1 Meta分析
Meta分析根據所建立模型的不同可以分為固定效應模型和隨機效應模型。下面分別介紹meta分析的這2種模型,并對它們進行比較。
1.1 固定效應模型
在固定效應模型下,假設所有的研究都來自于同一個總體[8],那么它們估計的效應量μ是相同的,也就是說μ1=μ2=…=μK=μ,實驗數據來自均值為μ方差為σ2的分布,即xij~F(x;μ,σ2),觀測效應Ti的分布為Ti~F(x;μ,vi)。在這種模型下只有一種誤差即組內誤差。如圖1所示,總體是均值為μ方差為σ2的分布,觀測效應為Ti,ei為隨機誤差,也就是組內誤差,觀測效應Ti的表達式為
Ti=μ+ei
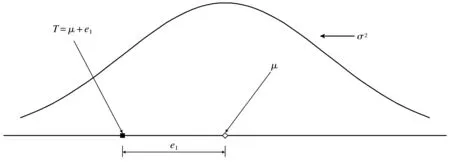
圖1 固定效應模型Fig.1 Fixed effect model
研究中通常用樣本量來作為權重,例如攜帶1 000個個體的研究得到的權重會是攜帶100個個體的研究的權重的10倍。但是這種方法并不精確,因此meta分析提出運用每組研究的方差的倒數來作為每組研究的權重[9],也就是說第i個研究的權重wi為
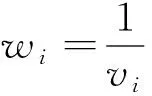
(1)
其中vi為第i組研究中子效應的方差。
Meta分析的計算方法及步驟如下[10-12]:
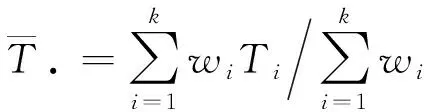
(2)
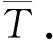
聯合效應的方差為權重和的倒數,表達式為
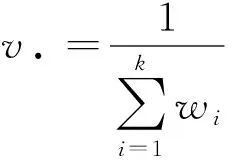
(3)
推導過程如下:
聯合效應的標準誤差為
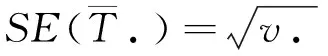
(4)
則95%的置信區間為
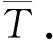
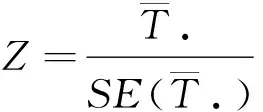
(6)
單尾檢驗p值為
p=1-Φ(|Z|)
(7)
雙尾檢驗p值為
p=2[1-Φ(|Z|)]
(8)
其中Φ為標準正態分布的分布函數。
1.2 隨機效應模型
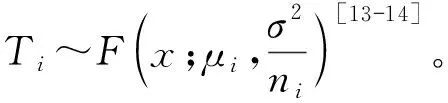
Ti=μ+εi+ei
其中:εi為組間誤差;ei為組內誤差。

圖2 隨機效應模型Fig.2 Random effect model
隨機效應模型將誤差分為2個部分,組內誤差和組間誤差,當分配權重的時候也是運用這2個部分來計算,這樣會更加精確。設總方差為Q,其公式如下
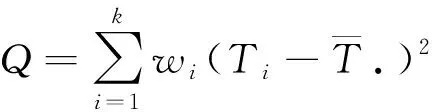
(9)
它是由組內方差和組間方差相加得到的,如果方差的來源只有組內方差,那么Q的期望值就會等于自由度df,其中
df=(NumberStudies)-1
證明如下:
其中
帶入(10)式得
其中總方差Q減去自由度df得到的是額外方差,也就是組間方差,記為τ2,其表達式為
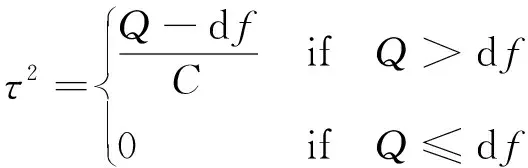
(11)
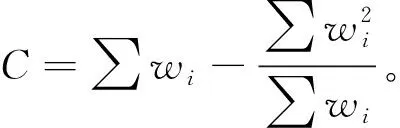
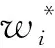
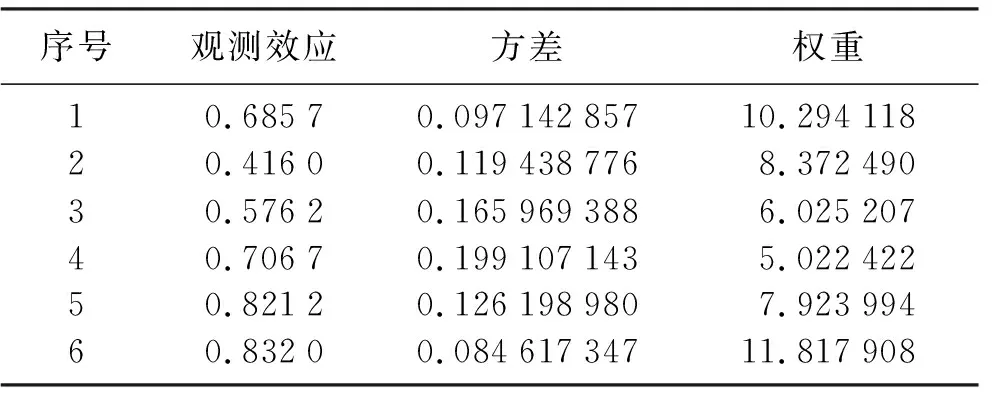
表1 植物種群密度和植物質量對植物代謝率的影響
由于隨機效應模型的計算公式與固定效應模型的形式一致,這里不再重復。
2 實例分析
表1是2012年統計的植物種群密度和植物質量對植物的代謝率的影響[16],其中原假設為植物種群密度和植物質量對植物的代謝率無影響,備擇假設為植物種群密度和植物質量對植物的代謝率有影響。
若將該研究模型看作固定效應模型,利用R語言進行計算,每一組的權重可以根據式(1)給出,根據式(2)到式(8)其他計算結果為
v=0.020 2
LowerLimit=0.678 6-1.96*0.142 2=0.399 9
UpperLimit=0.678 6+1.96*0.142 2=0.957 3
P1T=1-(Φ(|4.772 4|))<0.000 1
P2T=2[1-(Φ(|4.772 4|))]<0.000 1
由于2個p值都小于0.000 1,所以拒絕原假設,也就是說有理由相信植物種群密度和植物質量對植物的代謝率有影響。
若將其看做隨機效應模型,由式(9)得到總方差Q的值為
因該模型自由度為5,大于總方差Q,由式(10)知,組間方差τ2為0,所以該模型為固定效應模型。
3 結 語
因固定效應模型假定所有研究都來自一個總體,即影響每個研究的效應的元素是相同的,所以估計值也就是聯合效應是相同的,模型誤差僅來自于每個研究固有的隨機誤差,即組內誤差。但隨機效應模型假定每個研究來自不同總體,所以得到的是一個分布,估計值是分布的均值,模型的誤差不僅來自于組內誤差,還來自于研究與研究間的組間誤差。另外,在處理一些比較極端的實驗時,固定效應模型會忽視一些比較小的研究,但是隨機效應模型不會,因此隨機效應模型的權重會比固定效應模型平衡一些。
因此當選擇固定效應模型來進行計算時,有理由相信所有研究的功能是相同的,研究的目的是計算共同的效應然后將其推廣到其他相同總體的例子中。如選擇隨機效應模型,由于數據來自前人研究,所以研究功能不同,這些研究對象或干預可能會對結果有影響,對此研究目的是將其推廣到一系列不同總體中。但如研究數量較小,不太可能精確估計組間誤差,所以此時選擇固定效應模型。

