鈾濃縮工廠生產(chǎn)任務(wù)安排的簡單建模和求解

任寧 李世豪 毛樸

摘 要對(duì)鈾濃縮工廠各條生產(chǎn)線合理安排生產(chǎn)計(jì)劃可以有效提高生產(chǎn)效益，因此提出了采用線性規(guī)劃的方法建立多條生產(chǎn)線的生產(chǎn)任務(wù)安排計(jì)劃的數(shù)學(xué)模型，以確定每條生產(chǎn)線在各個(gè)工況和各個(gè)時(shí)間段的最佳生產(chǎn)計(jì)劃的安排方案。根據(jù)建立的線性規(guī)劃模型計(jì)算案例的最優(yōu)解，與平均分配法進(jìn)行對(duì)比。

關(guān)鍵詞鈾濃縮;生產(chǎn)計(jì)劃;線性規(guī)劃

0 引言

鈾濃縮工廠的任務(wù)就是生產(chǎn)豐度高于天然鈾品的一定豐度的鈾品。由于鈾濃縮工廠的每條生產(chǎn)線在不同工況下，產(chǎn)品的產(chǎn)量會(huì)有所不同。對(duì)于擁有多條生產(chǎn)線鈾濃縮工廠，合理安排生產(chǎn)任務(wù)的生產(chǎn)時(shí)間可以有效提高目標(biāo)產(chǎn)品的生產(chǎn)效益。目前國內(nèi)沒有相關(guān)的研究，本文采用線性規(guī)劃的方法建立了生產(chǎn)任務(wù)安排的模型，并通過求解案例來與平均分配法進(jìn)行對(duì)比，同時(shí)討論了建立的模型所適用的前提條件。

1 數(shù)學(xué)模型的建立

生產(chǎn)計(jì)劃的最優(yōu)化求解的數(shù)學(xué)模型的建立分為兩部分：約束條件和目標(biāo)函數(shù)的確定。其中約束條件是所建立的數(shù)學(xué)模型中的解必須滿足的條件。目標(biāo)函數(shù)則是評(píng)價(jià)滿足約束條件的解是否是最優(yōu)解的依據(jù)。對(duì)于鈾濃縮工廠的生產(chǎn)任務(wù)安排計(jì)劃，本文將各條生產(chǎn)線在各種工況的生產(chǎn)時(shí)間作為變量，確定相應(yīng)的約束條件和目標(biāo)函數(shù)，求解出各條生產(chǎn)線各種工況的安排時(shí)間的最優(yōu)解。

1.1 約束條件

1.1.1 任務(wù)量確定的約束條件

由于鈾濃縮工廠每條生產(chǎn)線在某種運(yùn)行工況下，目標(biāo)產(chǎn)品的流量基本不會(huì)有太大變化，可以認(rèn)為是定值，但目標(biāo)產(chǎn)品有任務(wù)量的要求，因此任務(wù)量所確定的約束條件為線性不等式方程組。也即是：

1.1.2 時(shí)間限期確定的約束條件

目標(biāo)產(chǎn)品的產(chǎn)量還有時(shí)間限制，因此需要確定各條生產(chǎn)線的分配生產(chǎn)時(shí)間與限制時(shí)間的約束條件。由于各個(gè)生產(chǎn)任務(wù)的時(shí)間限制不盡相同，如果不對(duì)各個(gè)生產(chǎn)任務(wù)進(jìn)行排序的話，計(jì)算量較大。本文根據(jù)生產(chǎn)任務(wù)安排的實(shí)際情況，將各個(gè)生產(chǎn)任務(wù)按照限期的先后順序確定，則可以建立各條生產(chǎn)線的分配生產(chǎn)時(shí)間與限制時(shí)間的約束條件的不等式方程。

1.2 目標(biāo)函數(shù)

對(duì)于鈾濃縮工廠的生產(chǎn)任務(wù)安排，目標(biāo)函數(shù)的計(jì)算基礎(chǔ)有多種選擇：可以選擇分離功，也可以選擇以某種豐度的六氟化鈾濃縮為目標(biāo)產(chǎn)品的產(chǎn)量。本文以后者為基礎(chǔ)確定目標(biāo)函數(shù)。方法為：先預(yù)期在未來某種豐度的產(chǎn)品的需求量最大，將生產(chǎn)任務(wù)安排后剩下的時(shí)間用來生產(chǎn)該需求量最大的產(chǎn)品，當(dāng)剩余時(shí)間用來生產(chǎn)預(yù)期需求量最大的產(chǎn)品的產(chǎn)量達(dá)到最大值時(shí)，此時(shí)生產(chǎn)任務(wù)安排即為最優(yōu)。按上述方法得到的目標(biāo)函數(shù)是線性函數(shù)，即：

2 數(shù)學(xué)模型的求解

由于建立的數(shù)學(xué)模型的約束條件和目標(biāo)函數(shù)均為線性函數(shù)，因此，該數(shù)學(xué)模型的求解也就是線性規(guī)劃求解。單純形法是人工求解線性規(guī)劃的常用方法。單純形法的基本原理是線性規(guī)劃問題的可行解集（若非空）是凸集[1]，也即是線性規(guī)劃問題的其中的一個(gè)極點(diǎn)必然為最優(yōu)可行解集。因此對(duì)于m個(gè)約束條件，必然有m個(gè)解，其他解均為0。對(duì)于上文建立的數(shù)學(xué)模型，采用單純形法需要加入人工變量，將線性規(guī)劃方程化為標(biāo)準(zhǔn)型才可求解。單純形法適用于生產(chǎn)任務(wù)和生產(chǎn)線較少的運(yùn)算，由于鈾濃縮工廠的約束條件方程個(gè)數(shù)為（n+1）·m，因此對(duì)于多條生產(chǎn)線的多個(gè)生產(chǎn)任務(wù)的數(shù)學(xué)模型，借助于matlab、lingo或excel等軟件求解相對(duì)更為方便、快捷，且準(zhǔn)確率更高。

3 計(jì)算案例

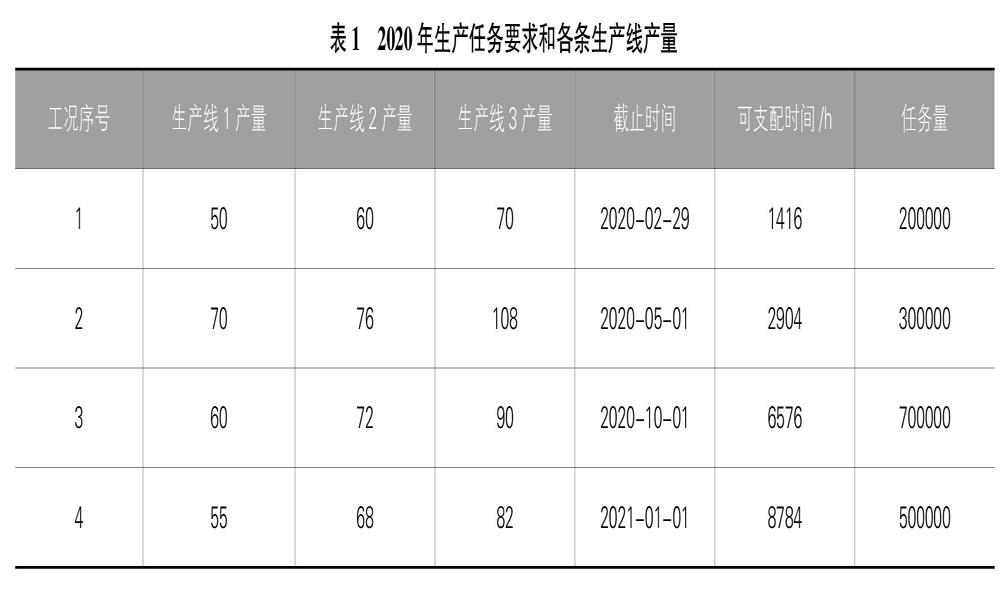
假設(shè)某個(gè)鈾濃縮工廠有三條生產(chǎn)線，從2020年1月1日0：00開始按照生產(chǎn)任務(wù)要求安排生產(chǎn)計(jì)劃，具體的生產(chǎn)任務(wù)量、生產(chǎn)截止時(shí)間要求和各工況下各條生產(chǎn)線相應(yīng)的預(yù)計(jì)生產(chǎn)量如表1所示。

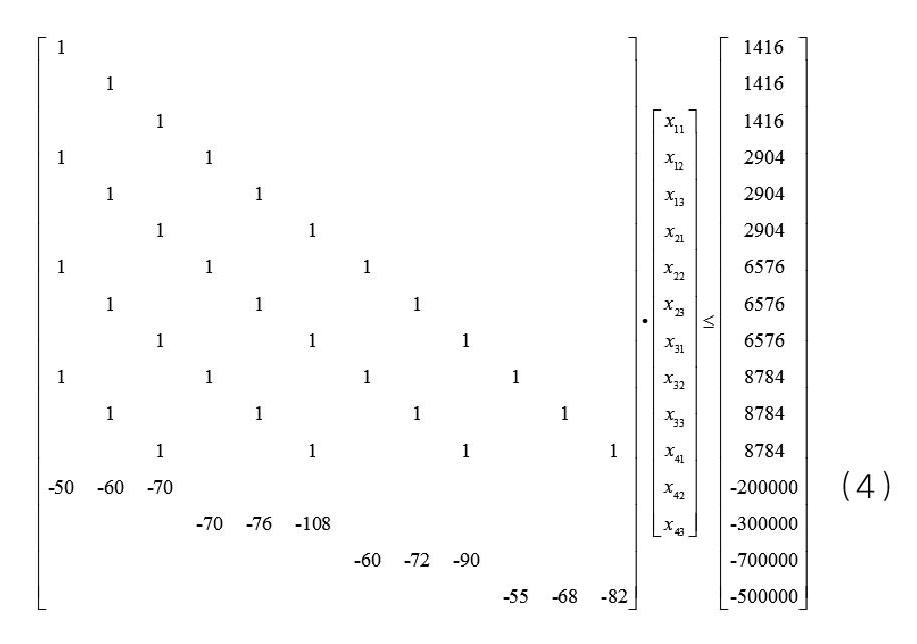
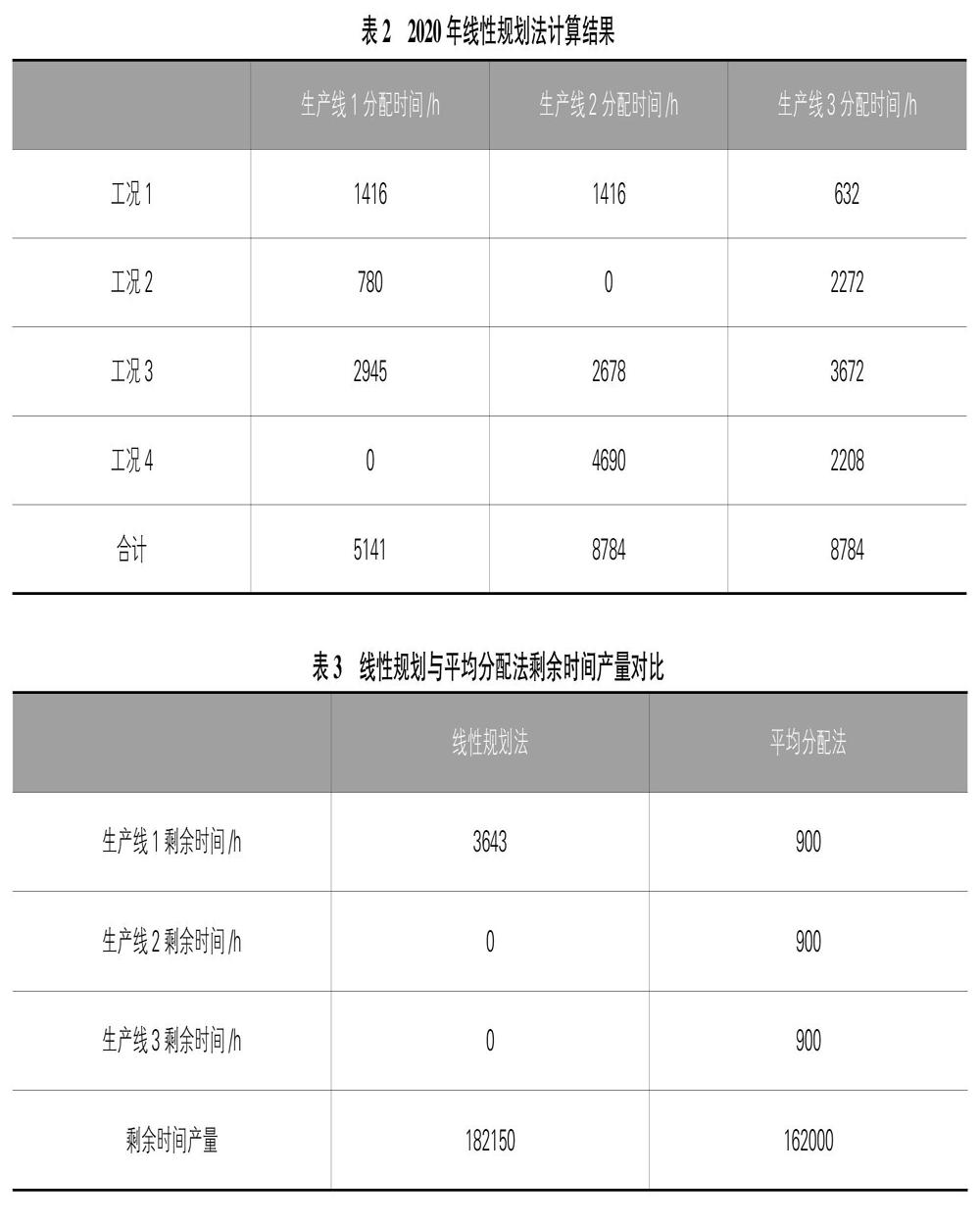
表1中工況序號(hào)代表各個(gè)工況按照截止時(shí)間進(jìn)行的排序。預(yù)計(jì)2021年的工況1產(chǎn)品的需要量最大，也即是安排2020年完成生產(chǎn)任務(wù)后的剩余時(shí)間全部用來生產(chǎn)工況1的產(chǎn)品。根據(jù)前文建模思路建立相應(yīng)的線性規(guī)劃方程如式（4），求解的生產(chǎn)任務(wù)時(shí)間安排如表2。

平均分配法則是對(duì)每條生產(chǎn)線完成每個(gè)生產(chǎn)任務(wù)分配相同的時(shí)間，這里也假設(shè)2020年完成生產(chǎn)任務(wù)的剩余時(shí)間全部用來生產(chǎn)工況1的產(chǎn)品。線性規(guī)劃與平均分配法的剩余時(shí)間利用結(jié)果如表3所示。

對(duì)于完成生產(chǎn)任務(wù)后的剩余時(shí)間，采用線性規(guī)劃法和平均分配法用以生產(chǎn)目標(biāo)產(chǎn)品，在這個(gè)計(jì)算案例中，線性規(guī)劃法的剩余時(shí)間產(chǎn)量約為平均分配法的1.124倍。

4 結(jié)論

建立的線性規(guī)劃模型并求解出來的生產(chǎn)任務(wù)安排明顯優(yōu)于平均分配法，可以用來判斷預(yù)期某工況對(duì)應(yīng)的流量在時(shí)間期限內(nèi)是否能完成生產(chǎn)任務(wù)，也可以找到最優(yōu)的生產(chǎn)任務(wù)安排方式，提高單位時(shí)間多條生產(chǎn)線的產(chǎn)量，或者在產(chǎn)量富余時(shí)，為合理降低主機(jī)負(fù)載提供決策依據(jù)。本文的研究結(jié)果預(yù)期可對(duì)鈾濃縮工廠生產(chǎn)計(jì)劃的編排起到積極的指導(dǎo)作用。

參考文獻(xiàn)

[1]《運(yùn)籌學(xué)及其應(yīng)用》朱求長，武漢：武漢大學(xué)出版社，2012.1：19.