對數正態分布貝葉斯更新方法比較研究

楊振中

摘 要設備可靠性數據是PSA定量化分析的基礎，對于可靠性數據，一般分為通用數據和電廠的特定數據。由于兩種數據在應用中均存在一定的缺陷，現在通用的做法是將通用數據作為先驗數據，然后結合電廠的特定數據貝葉斯更新得到后驗分布在PSA模型中使用。在操作實踐中，發現對數正態分布的通用數據，在進行后期的貝葉斯擬合時存在一定的困難。在工程實踐上，一般將其轉化為Gamma或Beta分布再進行處理，并形成了幾種成熟的解決方案。本文對對數正態分布轉化為Gamma分布的幾種方法做了比較研究，并簡述其差異和特性。

關鍵詞貝葉斯方法;PSA;Gamma分布;Beta分布;對數正態分布

0 前言

隨著PSA技術在核電廠廣泛的推廣，PSA的應用也逐漸地深入，這就對作為PSA技術基礎的可靠性數據工作提出了更高的要求。現階段，國內各個電廠一級PSA模型基本已開發完畢，隨著電廠運行時間的積累，勢必伴隨著電廠的變更改造和設備可靠性數據的更新。電廠的變更改造是對模型結構的修改，而設備可靠性數據的更新即是對模型中數據的修改，通過這一過程，保證模型反映電廠實際，這也就是所謂的living PSA。PSA技術發展至今，針對數據的處理方法基本上有三種思路。第一種是采用國際上已發布的同型電廠通用數據，現在主流的就是美系的NUREG-6928、法系的EPS-900數據源，此外我國國家核安全局在國內機組運行數據統計的基礎上，于2016年發布了我們自己的通用數據;第二種是使用核電廠自己的運行數據做經典估計。對于第一種方法，同型電廠與自身電廠不可避免的存在差異，所以直接使用通用數據并不能完全反映特定電廠的所有特征。對于第二種方法，由于在最初階段電廠的運行時間并不長，并且核電廠設備的可靠性一般較高，所以收集到的可靠性數據較少，往往是沒有數據，使用經典估計存在著困難。最好的方法就是將第一種與第二種方法結合起來，這也就是在可靠性數據處理中最常用的貝葉斯方法。在這種方法中，將通用數據作為先驗數據，將電廠收集到數據作為特定數據，然后應用貝葉斯公式進行擬合，使得到的后驗數據同時包括了兩方面的特征。

使用貝葉斯方法時需將數據的先驗分布通過貝葉斯定理轉化為后驗分布。在貝葉斯處理中，存在一種共軛分布的現象，就是對于既定的樣本數據的分布，存在一種先驗分布函數，使得后驗分布函數和先驗分布函數同屬于一個分布族。對于運行失效來說，這個分布是Gamma分布，對于需求失效而言，為Beta分布。對于Gamma和Beta分布，其通過貝葉斯轉化之后仍為Gamma和Beta分布，可以說處理起來是非常方便的。但很多的數據源，如法國EDF、EPRI的數據，假設失效率的先驗分布是對數正態分布，對于這樣的數據，在貝葉斯轉化時存在一定困難。

本文在總結貝葉斯處理方法和原理的基礎上，對對數正態分布的先驗數據貝葉斯擬合的幾種主要方法做比較研究，并分析其優劣。

1 可靠性數據的三種典型分布

由定義可以看出，部件運行失效的概率服從泊松分布，λ是泊松分布的參數。而泊松分布的共軛分布是Gamma分布，所以對于運行失效率，常以Gamma分布來表示。

由定義可以看出，需求失效概率p服從二項分布，而二項分布的共軛分布是Beta分布，所以需求失效常以Beta分布來表示。

此外，在可靠性和維修性方面，隨機變量的對數可能符合正態分布，對此情況在可靠性數據的統計分析中也常應用對數正態分布。

1.1 Gamma分布

Gamma分布因其概率密度函數很像Gamma函數定義中積分號內的被積部分而得名。對于X服從形狀參數為α，尺度參數為β的Gamma分布，我們記為：

因其在數學上處理方便，且有兩個參數α，β的調節，適應范圍很廣，所以工程上常常將運行失效率的分布假設為Gamma分布，如美國所做的柴油發電機可靠性分析、IAEA-TE CDOC -478中收集的瑞典可靠性數據[1]。在意義上，Gamma分布可看作是泊松分布參數（單位時間內隨機事件發生率）的概率分布，且泊松分布的共軛分布即為Gamma分布。

1.2 Beta分布

1.3 對數正態分布

對數正態分布有如下特點。

對數正態分布是自變量取對數時，其故障密度函數符合正態分布的一種偏態性概率分布。它的故障率基本屬于遞增型的，但遞增的速度是變化的，先快后慢然后趨于平緩。對數變換可將較大的數縮小為較小的數，且越大的數縮小的越多，這一特性可以使較為分散的數據通過對數變換相對的集中起來，所以常把跨幾個數量級的數據用對數分布去擬合。在機械零件及材料的疲勞壽命中，對數正態分布應用的較多。在核電廠設備可靠性參數、共因參數方面，對數正態分布同樣有著大量的應用。

2 貝葉斯方法

Bayes方法在20個世紀50年代提出，用于解決復雜系統的可靠性評估問題，在處理小樣本數據時具有明顯優勢，在武器和航天等領域取得很好的評估效果和經濟效益。經過半個多世紀的發展，Bayes小樣本理論已經形成了比較成熟的研究體系。

Bayes方法同經典的統計理論的區別是所求參數的本身被看成隨機變量，如單元的壽命，求得的后驗分布為參數的概率分布區間。Bayes方法利用了先驗分布，不需要很大的樣本也可以得到較好的概率估計值。相比經典方法而言，Bayes方法的優勢在于能夠充分利用各類先驗信息，包括可靠性試驗數據、歷史數據、專家信息和仿真試驗信息等，降低了經典方法對現場試驗樣本容量的依賴程度，使得在相同評估精度要求條件下，現場樣本容量可以相對減少。需要強調的是，Bayes方法不是少用信息，而是充分運用產品試驗過程中的各類信息（可靠性試驗數據、歷史數據、專家信息和仿真信息等），因而在實際工程可以得到較好的應用[2]。

連續分布的貝葉斯公式是可靠性數據分析中經常用到的，因為對于部件的運行失效率λ和需求失效率γ（這里統一用θ表示）而言，在其可能的區間里，其分布顯然是連續的。設{x1，…，xn}代表一個樣本，它服從一個具有似然函數L、連續參數θ和先驗密度g（θ）的一個分布。那么，θ的后驗分布密度為：

對于對數正態分布作為先驗分布的情況，如果直接進行貝葉斯估計，需要進行煩瑣的數值積分，且得到的后驗分布不一定是正態分布，這樣會對今后進行PSA定量化的不確定性分析帶來困難[2]。在工程上，對于對數正態分布的情況，一般的解決方法是將其轉化為Gamma分布和Beta分布，由于在設備可靠性較高的情況下，Beta分布可近似看作Gamma分布處理，所以本文著重討論對數正態分布轉化為Gamma分布的情形。

3 對數正態分布為先驗分布的貝葉斯處理

工程上，如果先驗分布是對數正態分布，一般將其轉化為Gamma分布，然后進行貝葉斯處理。這一轉化過程，采用的是一種數學上的近似，在實踐領域也有了多種成熟的方法。

3.1 轉化方法

1）EF值轉化法：在這種方法中，令轉化前后的mean值和EF值相等。

由于先驗分布的mean值和EF值已知，所以問題轉化為已知Gamma分布的mean值和EF值，求取α和β。

Gamma分布均值mean，誤差因子EF，由于mean已知，只需通過EF求取出α，即可確定β。這里我們可以選用查表的方法，也可以選用數值計算對α的數值進行搜索。

清華大學就EF值轉化法進行過成功應用，并且已經在大亞灣核電廠的數據處理中進行了實踐[3]。

2）95%分位點轉化法：在轉化過程中，使這兩種分布在兩個關鍵點（均值和95%分位點）上重合，找到滿足上述條件的Gamma分布參數α，β，即完成了將先驗分布的對數正態分布轉換為Gamma分布的工作。

在具體轉化時，同樣已知均值mean和EF，利用對數正態分布的函數關系，求出其x0.95，利用參考文獻[4]中與α的關系曲線，可以求得α值。再根據已知的mean關系，即可得出Gamma分布。同方法1），也可以利用數值計算的方法完成對α的搜索。

在國內，機械科學研究院與秦山核電壓水堆電廠即秦山一二期與方家山電廠的數據處理采用該種方法。

3）方差轉化法：這種方法是令轉化前后的均值和方差相等。由已知LN分布的均值和EF值，可以方便地求出其方差。再利用Gamma分布均值mean，可以順利地求出α和β。通過三種方法的比較，可以看到此種方法最為簡便。在實際應用中，秦山三期重水堆采用的是該種方法。

3.2 三種轉化方法的比較

1）三種方法的準確性分析

假設一均值mean=0.5，誤差因子EF=3的對數正態分布，當累計失效次數為2，累計運行小時數為2500時，得到如下后驗分布圖像。

由圖1可以看出，當失效數據較小時，三種轉化方法差異不大，與LN分布經數值積分后的貝葉斯轉化結果也無明顯偏差。

假設對數正態分布的均值和誤差因子不變，當累計失效次數為6，累計運行小時數為4500時，得到如下圖像。

由圖2可知，當失效數據較大時，EF值轉化法與LN經數值積分后的結果最為接近，95%分位點法次之，總體上這兩種方法差異不大，而方差轉化法的誤差偏大。

2）LN分布EF值與Gamma分布α值相關性比較

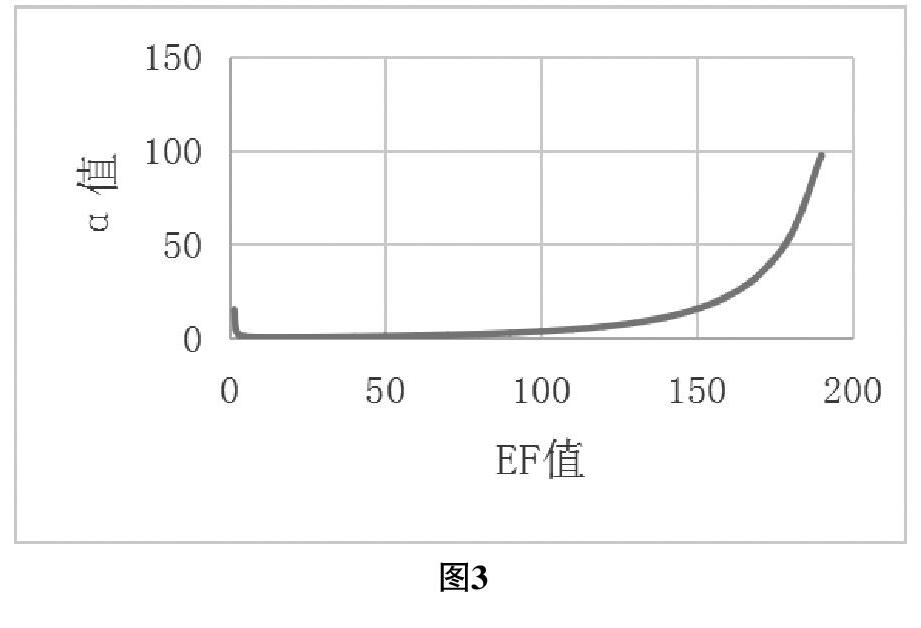
設先驗數據的分布類型為對數正態分布，其先驗均值為0.5，利用EF值轉化法，可得EF關于α的關系曲線如圖3所示。

由圖3可以觀察到，當EF值較小時，α值是關于EF值的減函數，隨著EF值的增大，α值的變化有一個相對平緩的區間，此時的α相對于EF的變化敏感性不強。隨著EF值繼續增大，α值有一個迅速增大的過程，從形態上來看，呈現出指數增長的特征。

4 結論

在針對核電廠小樣本失效概率分析的情況下，貝葉斯方法有著其明顯的優越性，所以在核電廠PSA分析中有著廣泛的應用。但是當先驗分布為對數正態分布的情況，在求取后驗分布時又面臨著數學上的困難。為此工程上形成了三種行之有效的解決方案。經過對三種方法進行對比，發現EF值轉化法較為復雜，但所得結果準確性較高;95%分位點法次之;方差轉化法最為簡單，但形成的偏差也最大。此外，研究發現，LN分布的EF值與轉化后Gamma分布的α值并不呈單調關系，前部隨著EF值增大會有一個遞減的過程，且當EF值增大超過一定數值后，α將會呈現一個指數增大的過程。

參考文獻

[1]馬靜嫻，閆國奎，劉志軍.用貝葉斯方法處理核電站PSA分析中的設備可靠性數據[J].2004年全國機械可靠性學術交流會論文集.

[2]劉方亮.核電廠小樣本數據Bayes處理方法應用研究[D].清華大學碩士學位論文，2010年.

[3]茆定遠，薛大知.核電站PSA分析中可靠性數據處理的貝葉斯方法，核動力工程Vol.21.No.5 Oct.2000.

[4]Some Properties of Distributions Useful in the Study of Rare Events，IEEE Transaction on Reliability Vol.R-31，No.1，APRIL 1982.