深埋復合式襯砌隧道二襯分擔比研究

周 建，楊新安,蔡 鍵，楊 帆

(1.同濟大學 道路與交通工程教育部重點實驗室，上海 201804；2.浙江溫州沈海高速公路有限公司，浙江 溫州 325000)

0 引言

復合式襯砌是礦山法施工隧道主要采用的支護方式，初期支護(簡稱初支)和二次襯砌(簡稱二襯)是復合式襯砌的主要組成部分[1-3]。一般情況下，初支基本穩定后施加二襯，當初支具備一定強度后，初支將一部分圍巖壓力轉移至二襯，形成“圍巖+初支+二襯”的復合式承載結構。然而，關于二襯承擔圍巖壓力的比例(二襯分擔比)至今存在諸多疑惑。

在隧道設計過程中，二襯分擔比對隧道支護參數的選擇具有直接影響，長期以來二襯分擔比均通過實測數據確定，如房倩等[4]通過對鐵路隧道6個不同斷面初支、二襯間接觸壓力的監測，得到在一定條件下初支和圍巖承擔全部荷載、二襯作為安全儲備的結論；孫毅等[5]將監測結果與數值模擬結果進行對比分析，發現實測的鐵路隧道二次襯砌受載量遠小于其承載極限能力；何本國等[6]對深埋鐵路隧道現場支護結構荷載量測試驗，得出二襯作為重要支護形式平均分擔50.1%荷載的結論；Prof[7]指出:噴射混凝土與二襯復合體視為承受全部荷載的永久支護；劉善琪[8]采集齊岳山隧道3個斷面的圍巖與初支、初支與二襯之間的壓力，得到二襯最大承受30%左右的壓力；田鵬[9]依托蘭新鐵路第二雙線大梁隧道，得到二次襯砌圍巖壓力分擔比例平均值在45.0%～70.3%的結論。上述學者根據依托工程實例監測數據，得到各自的二襯分擔比，然而監測數據僅對所建工程服務，故不能作為指導工程實踐的依據。劉學增等[10]基于山嶺公路隧道圍巖壓力的監測數據，得到不同級別圍巖二襯分擔比，但研究內容僅限于山嶺公路隧道，存在局限性；李鵬飛等[11]根據圍巖壓力監測數據，得到圍巖壓力的分布規律，但難以預測隧道二襯分擔圍巖壓力的比值；所以，關于能夠指導工程實踐的隧道二襯分擔比的建議值有待進一步研究。

2010版《公路隧道設計細則》(JTG/T D70—2010)[12]和2016版《鐵路隧道設計規范》(TB1003—2016)[13]均認為I～Ⅲ級圍巖二襯可作為安全儲備，而IV級及以上等級圍巖《公路隧道設計細則》(JTG/T D70—2010)僅給出雙車道二襯分擔比建議值，《鐵路隧道設計規范》(TB1003—2016)提出二襯根據地質情況宜按荷載結構設計，兩種主流隧道規范未能明確給出IV級及以上軟弱圍巖二襯分擔比建議值。本研究認為在隧道工程建設所處地質條件越來越復雜的新形勢下，IV級及以上軟弱圍巖二襯分擔比建議值有待完善。

本研究根據深埋隧道圍巖與初支、初支與二襯的監測數據，列出了不同圍巖級別隧道斷面圍巖壓力隨埋深、跨度變化的分布散點，并與經驗公式計算值對比，探究經驗公式的適用性；另外，探討了不同圍巖級別隧道的二襯分擔比分布區間，運用“疊合梁”理論與實測數據的二襯分擔比進行對比分析，并對“疊合梁”理論的適用性作出評價。

1 初支與二襯荷載的傳遞機理

現階段，關于二襯分擔比理論方面研究十分有限，僅有“疊合梁”理論來分析初支與二襯荷載之間的關系，部分研究成果均有提及[14-16]，但尚未通過大量實測數據來證明該理論的適用性。

文獻[17]研究根據復合式襯砌特點，初支結構幾乎通過徑向傳力于二襯結構，從而使得初支與二襯組成“疊合梁”式結構，提出了初支荷載傳遞至二襯的理論方法，并作出如下假定：(1)初支與二襯為圓形梁單元并緊密貼合；(2)復合式襯砌所受外力為均布壓力。“疊合梁”力學模型如圖1所示，圖中r0，r1和r2分別為隧道、初支內邊緣和二襯內邊緣的等效半徑。

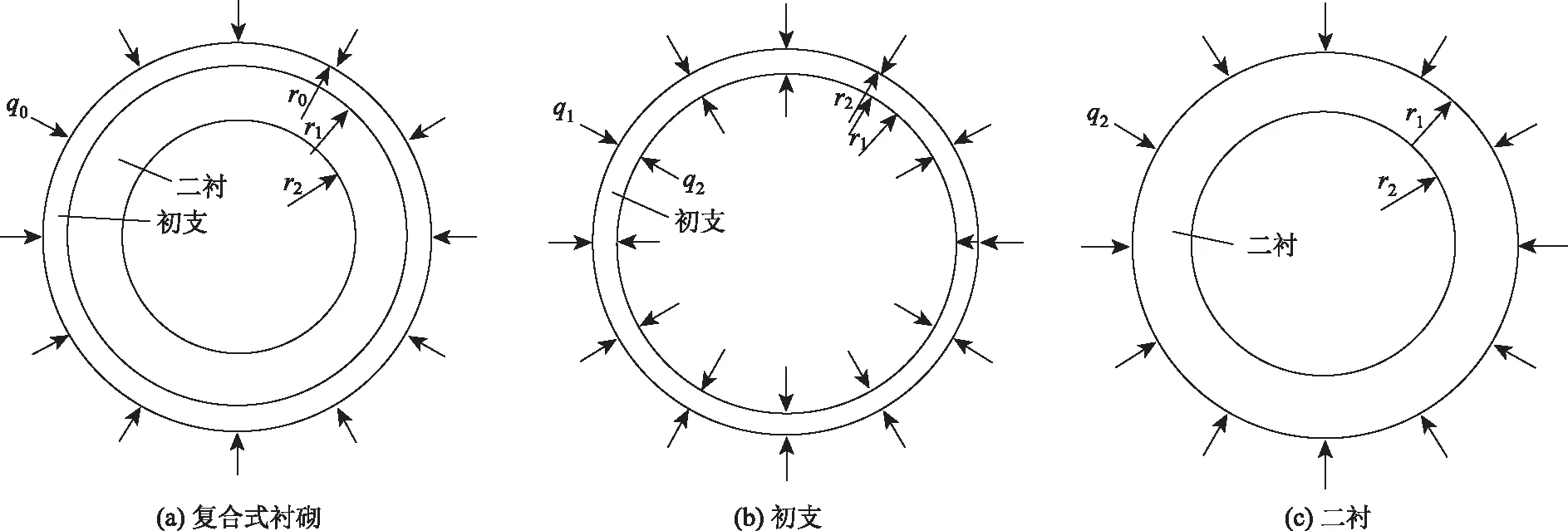
圖1 “疊合梁”結構力學模型Fig.1 Structural mechanical model of “composite beam”

在大多數情況下，隧道洞室斷面為非圓形，本研究整理的隧道斷面形狀為馬蹄形或直墻拱形，在計算洞室塑性區半徑時通常將非圓形斷面按某種標準等效成圓形斷面，對于馬蹄形和直墻拱形斷面常采用外接圓半徑法，如圖2所示。圖中實線為斷面真實的形狀，虛線為等效圓的形狀。

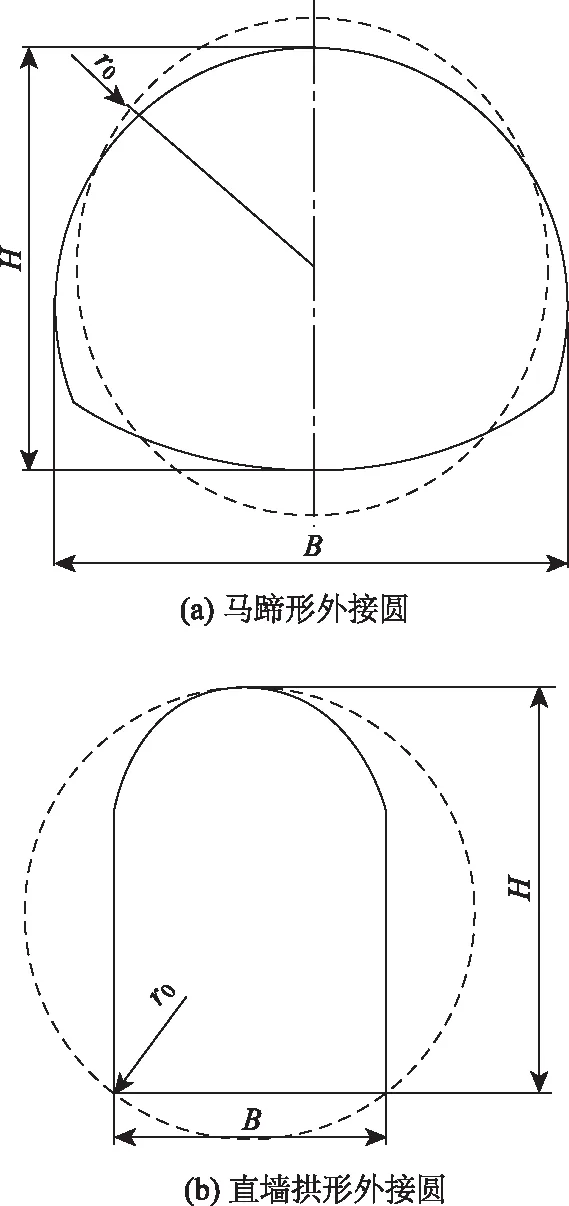
圖2 外接圓半徑法示意圖Fig.2 Schematic diagram of circumscribed radius method

文獻[18]指出:高跨比在0.8～1.25之間的隧道其等效圓計算半徑可以參考以下公式：

(1)

式中，H，B分別為隧道斷面高度、寬度。

對于大跨度或高邊墻的隧道斷面，通過典型類比法得到此類隧道的半徑公式為：

(2)

根據“疊合梁”理論，初支結構在作用力q1和q2作用下，其內邊緣位移U1為：

(3)

二襯外邊緣位移U2為：

(4)

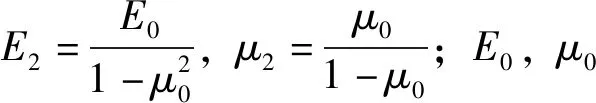
根據初支與二襯接觸面位移變形協調條件:U1=U2，可求得q2，定義二襯荷載分擔比G0為：

(5)

則二襯荷載分擔比的表達式為：

(6)

2 深埋隧道二襯分擔比分析

2.1 深埋隧道圍巖壓力監測數據分析

初支與圍巖間的接觸壓力是計算深埋隧道二襯分擔比的重要組成部分，一般情況下，通過計算洞壁所受圍巖壓力q1來等效初支與圍巖間的接觸壓力，所以，工程實踐十分重視圍巖壓力的監測與計算，設計人員常依據《公路隧道設計規范》(JTG/T D70—2010)、太沙基公式、普氏理論等圍巖松弛壓力經驗公式預測圍巖壓力，雖然計算結果常與實測值存在差距，但目前尚未建立符合客觀實際情況的圍巖壓力理論方法，李鵬飛等[19]給出了埋深、跨度等參數不同時經驗公式的適用范圍，但沒有給出監測數據的驗證；因此，經驗公式是否適用于深埋巖質隧道仍值得探究。本節以深埋隧道初支與圍巖監測數據為基礎，對隧道斷面主要受力部位(左拱腳、左邊墻、左拱腰、拱頂、右拱腰、右邊墻和右拱腳)圍巖壓力監測數據進行整理，共統計31座隧道120個斷面，統計樣本如表1所示。斷面分布按圍巖級別分類如下：Ⅲ級圍巖43個，Ⅳ級圍巖34個，Ⅴ和Ⅵ級圍巖43個(其中Ⅵ級圍巖6個)。由于本研究的隧道范圍為深埋隧道，因此，將斷面各測點圍巖壓力的平均值作為統計數據。最后，將圍巖壓力實測值與《公路隧道設計細則》(JTG/T D70—2010)、太沙基理論、普氏理論經驗公式的計算值對比分析，試圖尋找圍巖壓力實測值與經驗公式計算值的某種聯系。

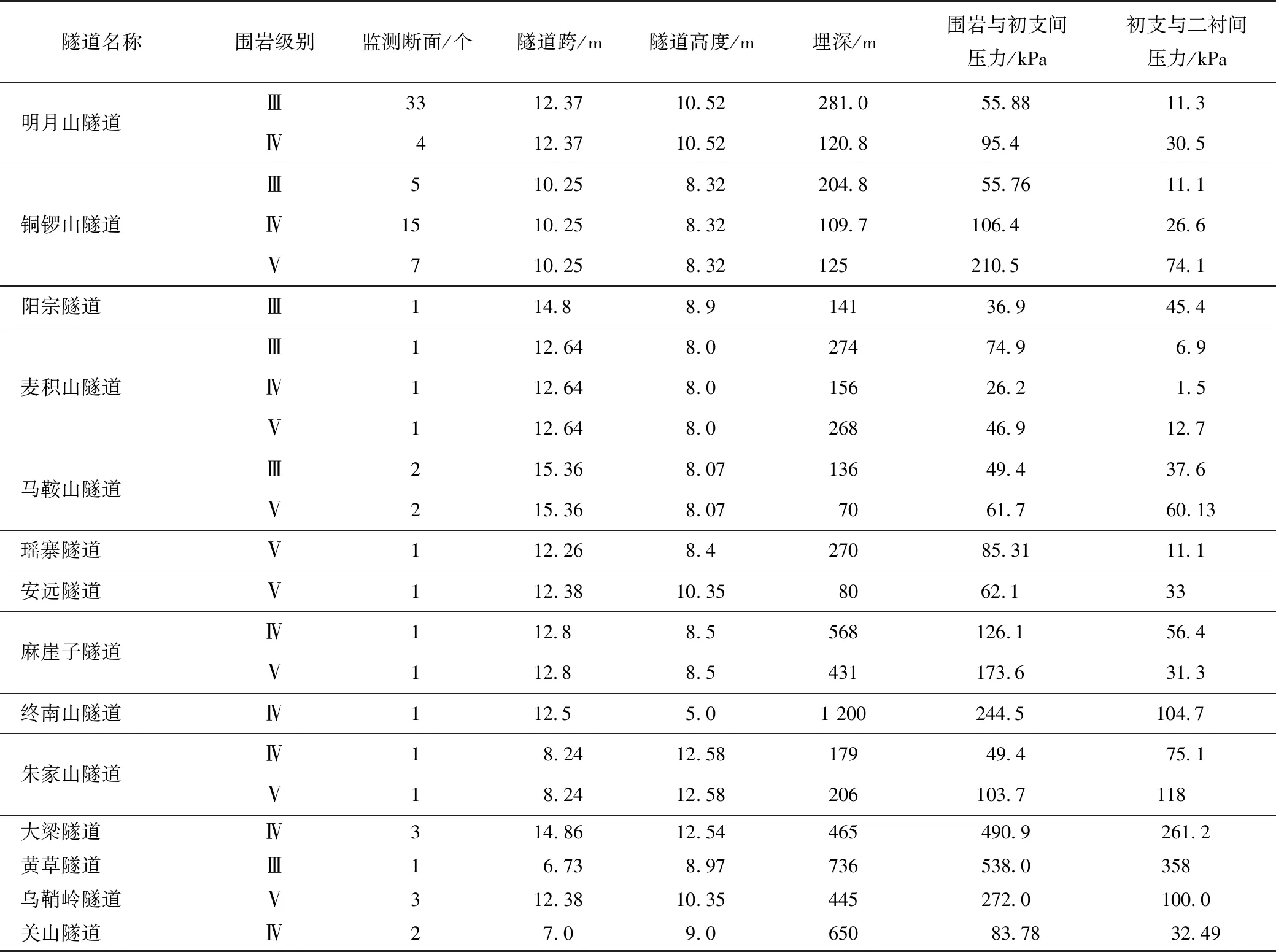
表1 深埋隧道支護監測樣本

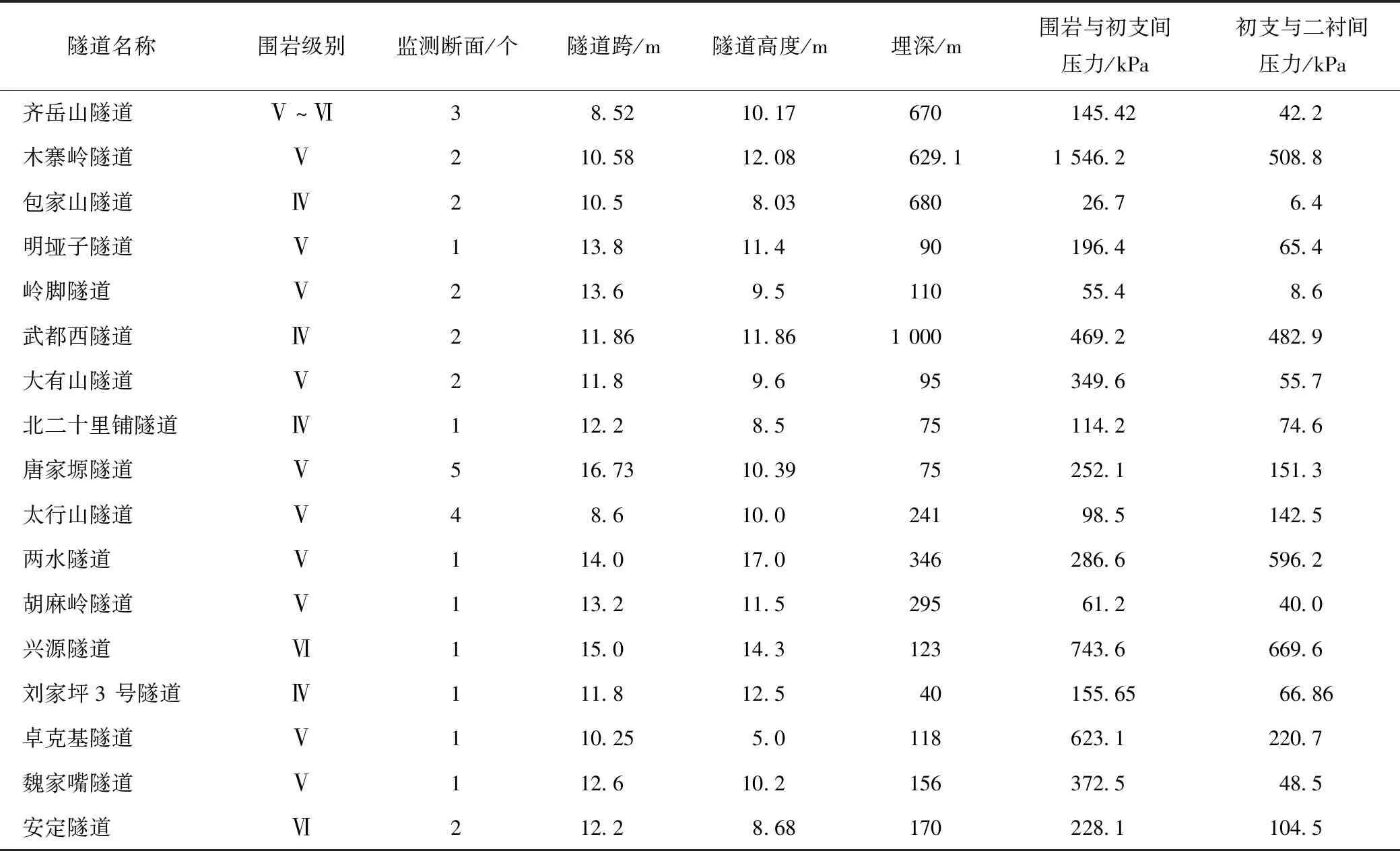
續表1

從表1不難看出，深埋復合式襯砌隧道支護結構接觸壓力總體隨著圍巖級別或隧道埋深的增加而增加，而與隧道跨度﹑高度無明顯聯系。

為簡化理論計算，作如下假設：(1)對于深埋隧道，將隧道中心的埋深記為隧道埋深；(2)統計的圍巖壓力是各斷面監測部位圍巖壓力的平均值。圍巖的物理力學參數可參考隧規，各參數均設定為均值，如表2所示。

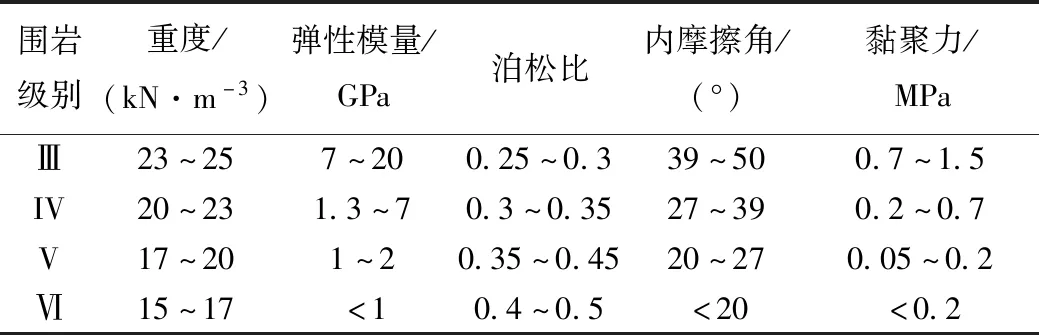
表2 圍巖物理力學參數

通過側向壓力q1/B(單位:kPa/m)來間接反應圍巖壓力的變化，如圖3所示。圖3中(a)、(b) 和(c)依次為Ⅲ，IV，V和Ⅵ級側向圍巖壓力q1/B與埋深H之間的關系圖(為了保持較好的擬合度，剔除少數壞點)。

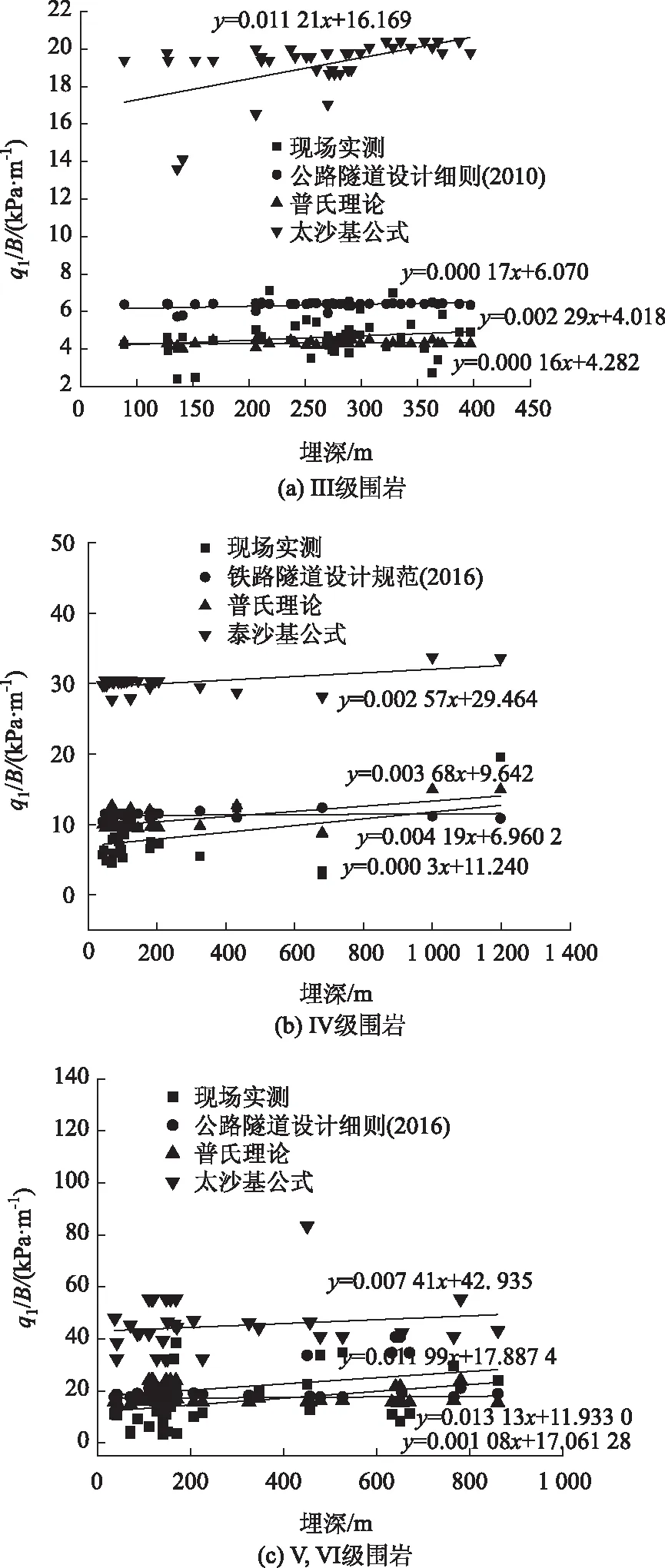
圖3 圍巖側向壓力q1/B與埋深H之間的關系Fig.3 Relationships between lateral pressure q1/B and buried depth H of surrounding rock

對圍巖壓力的數據分析可得出：隨著埋深的增加，圍巖壓力總體呈增大的趨勢，不過增大幅度不大。少數斷面(圖3未列出)在埋深不大情況下圍巖壓力卻較類似斷面大很多，其原因是受高地應力的影響。從圖3中不難看出，經驗公式計算值與實測值接近程度從優到劣依次為：普氏理論、《公路隧道設計細則》(JTG/T D70—2010)、太沙基公式。普氏理論計算值雖然較接近實測值，但在埋深部分區段甚至低于實測值，不利于工程實踐預測。對于Ⅲ，Ⅳ級圍巖，太沙基公式計算值是實測值的4倍左右，Ⅴ，Ⅵ級圍巖太沙基公式計算值是實測值的2～3倍，其若作為指導工程實踐的依據，則極不經濟。至于太沙基公式為何與實測相去甚遠，隧規認為：Ⅰ～Ⅳ級圍巖中的深埋隧道，圍巖壓力為主要形變壓力，而Ⅳ～Ⅵ級圍巖中深埋隧道的圍巖壓力為松散荷載，太沙基公式將圍巖視為松散體，主要考慮重力作用，所以，巖石越完整，沙基公式計算值與實測值相差越大。在埋深800 m以內，《公路隧道設計細則》(JTG/T D70—2010)計算值一般是實測值的1.3～1.5倍，埋深超過1 000 m，此規范難以適用，因此，滿足埋深小于800 m時，《公路隧道設計細則》(JTG/T D70—2010)預測圍巖壓力較為合適。

為了提高從初支到二襯荷載傳遞理論的精確性，現在上述經驗公式中選取合適的計算公式，根據圖3線性擬合變化的特點，將普氏理論計算值修正為：

(7)

2.2 二襯分擔比數據分析

關于“疊合梁”理論部分文獻多有提及，但對該理論的適用性尚未作出系統評價，通過對深埋隧道不同圍巖級別二襯分擔比的實測數據與“疊合梁”理論對比分析，試圖驗證“疊合梁”理論的適用性，數據對比如圖4所示。

圖4 “疊合梁”理論和現場實測的二襯分擔比散點分布圖Fig.4 Scatter diagrams of secondary lining sharing ratio obtained by“composite beam” theory and field measurement

根據圖4實測值與“疊合梁”理論計算值散點分布可知:

(1)從實測數據可以看出，隨著圍巖級別的增大，二襯分擔比G0越大，Ⅲ，Ⅳ，Ⅴ和Ⅵ級圍巖的G0多集中于20%～30%，30%～45%，40%～70%；雖然Ⅲ級圍巖二襯結構承受荷載相對不大，且隧規認為“Ⅲ級圍巖二襯結構可看作安全儲備”，圖4(a)中數據驗證了這一說法的普遍性，但根據監測數據，仍有極少數斷面二襯分擔比因高地應力超過50%，個別斷面甚至達到83.7%的現象。因此，對于高地應力Ⅲ級圍巖隧道，二襯結構設計需謹慎對待。Ⅳ，Ⅴ和Ⅵ級圍巖少數斷面二襯分擔比超過100%，這是因為該部分隧道地應力高、圍巖條件差，初支未及時施作而導致二襯承擔較大荷載，超過了隧規提出的二襯分擔比建議值。以上從側面反映了分析二襯分擔比對支護設計有重要的指導作用。

(2)從“疊合梁”理論計算值與實測值對比可以看出：從數據總體反映來看，“疊合梁”理論計算值比實測值大，圍巖級別越小，G0差距更明顯，Ⅲ，Ⅳ，Ⅴ和Ⅵ級圍巖二襯分擔比“疊合梁”理論計算值是實測值的4倍、3倍和1.5倍左右。顯然，“疊合梁”理論不適用于計算Ⅲ，Ⅳ級圍巖二襯分擔比；在沒有高估初支結構承擔荷載能力的前提下，Ⅴ和Ⅵ級二襯分擔比的預測可由“疊合梁”理論計算值乘以0.7來實現。

2.3 “疊合梁”理論的問題分析

在運用“疊合梁”理論計算二襯分擔比時發現，二襯分擔比受支護材料物理力學參數的影響甚微，而受初支厚度D1與二襯厚度D2的影響頗大，在此，設計支護材料基本物理力學參數如表3所示，來探究二襯分擔比與D1，D2之間的關系，如圖5所示。

表3 隧道等效半徑及支護材料物理力學參數

圖5 二襯分擔比與初支、二襯厚度的關系曲線Fig.5 Curves of secondary lining sharing ratio vs. thicknesses of primary support and secondary lining

從圖5表面上看，在D1一定的條件下，D2越大，二襯分擔比G0越大；D2不變時，G0隨D1增大呈現減小的趨勢。進一步分析圖5 數據，可得到“疊合梁”理論存在以下兩方面缺陷：(1)對于巖性較完整的圍巖，初支足夠承擔圍巖荷載，增加二襯厚度并不能提高G0，而“疊合梁”理論G0卻有一定的增大幅度，與事實相悖。(2)根據2010版《公路隧道設計細則》有關隧道復合式襯砌厚度設計分析，二襯混凝土厚度是初支混凝土厚度的2～4倍，其中對于Ⅲ級以上的圍巖，D1在0.08～0.28 m之間，D2在0.35～0.60 m之間，對應到圖5中，G0應在60%以上，而Ⅲ，Ⅳ級圍巖G0基本在45%以下，圖5要想降低G0至Ⅲ，Ⅳ級圍巖水平，則需使得D2<0.3 m，D1>0.6 m，這與隧規嚴重不符。因此，可斷定“疊合梁”理論不適用于Ⅳ級及以下圍巖隧道二襯分擔比計算。

3 結論

本研究基于圍巖與初支、初支與二襯間接觸壓力的監測數據，獲得以下幾方面成果：

(1)通過經驗公式計算值與實測值的對比，經驗公式計算值與實測值接近程度從優到劣依次為：普氏理論、2010版《公路隧道設計細則》、太沙基公式；滿足埋深小于800 m時，2016版《鐵路隧道設計規范》預測圍巖壓力較為合適；計算復合式襯砌隧道二襯分擔比，圍巖與初支的接觸壓力可根據修正的普氏理論計算。

(2)通過對Ⅲ級以上圍巖二襯分擔比分析，Ⅲ，Ⅳ，Ⅴ和Ⅵ級圍巖的二襯分擔比多集中于20%～30%，30%～45%，40%～70%；在地應力較高或圍巖條件太差的情況下，二襯承擔主要荷載，因此，在隧道支護設計時應引起重視。

(3)將“疊合梁”理論計算值與實測數據的二襯分擔比進行對比，得出了巖性越完整的圍巖“疊合梁”理論計算誤差越大的結論。另外，“疊合梁”理論受支護厚度D1，D2的影響甚大，難以適用于Ⅳ級及以下圍巖二襯分擔比的計算，對于Ⅴ和Ⅵ級圍巖二襯分擔比的預測可由“疊合梁”理論計算值的70%來實現。