高邊坡爆破振動傳播規律及其控制技術

林海松

(南寧交通投資集團有限公司，南寧 530022)

控制爆破技術作為一種高效的施工技術，長期受到工程建設領域的青睞，被廣泛應用于水利水電工程、道路基礎設施建設、礦產開采及城鎮建(構)筑物的拆除等領域。在水利水電工程中，鑒于土石方開挖規模大、機械施工成本高、交通設施不便等原因，采用控制爆破技術進行巖土的開挖往往是較為安全、經濟及快速的施工手段。但是，爆破作業為工程及建設施工帶來巨大經濟及社會效益的同時，也會產生許多負面效應，如爆破振動、爆破飛石、沖擊波、噪聲、爆破煙塵等有害效應。隨著人民生活水平及我國社會經濟的不斷進步，相關法律、法規及行業標準嚴格規定了爆破有害效應的安全允許值。因此，分析、研究爆破有害效應的產生及衰減規律，進而提出對應的控制措施，減弱爆破危害，同時兼顧爆破效果是工程爆破領域的研究重點。爆破振動作為爆破過程中最為顯著的有害效應，近年來是爆破工程技術領域及科學研究領域的焦點。但由于炸藥爆炸過程的瞬時性，加上爆破作用的介質常常為巖石、土體，均為不連續介質，使爆破振動波傳播過程具有較大的模糊性、復雜性及隨機性。因此，開展爆破振動的相關研究工作十分困難[1]。

爆破振動的傳播及衰減受多種因素的影響，主要包括爆區地質情況、爆破時的最大段藥量、傳播距離及爆區地形地貌等。前蘇聯爆破專家薩道夫斯基提出：爆破所產生的質點振動峰值速度與爆破時的最大段藥量Q及爆源距R成函數關系。傳統的爆破振動研究方法則是通過大量的爆破振動監測數據，利用薩道夫斯基公式進行數據回歸，進而求解出相關的未知參數K、α的值[2]：

(1)

由于與爆破振動相關的因素較多，且其與爆破振動的傳播與衰減規律之間有著十分復雜的函數關系，加上相關基礎理論研究的不足，導致采用傳統經驗公式不能較為準確的預測爆破振動的傳播規律。周同齡等[3]、王在泉等[4]、唐海等[5]、張勤彬等[6]通過實際工程驗證，在爆破區域與爆破振動監測點間存在明顯高程差的條件下，采用傳統的薩道夫斯基公式進行爆破振動預測時，其結果精度較低。因此，在具有明顯高程差的爆破區域進行爆破振動相關研究工作時，應考慮高程效應對爆破振動傳播及衰減規律的影響。

1 反映高程效應的爆破振動分析

無論在科學研究還是工程技術領域中，每一個單一的物理量都和其他單一的各物理量之間存在著相互關系，利用特定的分析方法推導出因變量與自變量間的函數關系是其基礎研究的重點。量綱分析方法則是利用各物理量間所遵循的固定表達形式來分析各物理量之間的函數關系。在對某個特定的因變量進行分析時，必須系統完整地找出與之相關的各個自變量，并統一單位制，在量綱分析方法中，最重要的則是所有物理量的量綱需滿足齊次定理，量綱齊次定律中規定等式兩邊的量綱必須一致。π定理(又稱布金漢定理)提出了：一個實際問題中有n個自變量，已選取m個(n>m)具有獨立單位制的物理量存在，則該問題中存在有n-m個無量綱的變量[7]。

工程實踐及相關研究表明，采用傳統的薩道夫斯基公式表征爆破振動的傳播及衰減規律僅適用于場地較為平整的爆破區域。在爆破區域與監測點間存在明顯高程差的條件下，采用此預測經驗公式表征爆破振動的傳播規律十分不準確。因此，需引入高程差H表征對爆破振動傳播及衰減規律的影響。

在爆破振動傳播過程中，爆破所引起的建(構)筑物質點峰值振動速度v不僅和爆破最大段裝藥量Q、爆源距R、爆破振動波的傳播介質及爆破區域地質地形地貌有關，還和爆源與測點間的高程差H、巖體的密度ρ、爆破振動波波速c、炸藥爆轟時間t有關[6]，根據量綱分析可得出10個與爆破振動波相關的物理量(見表1)。

表1 爆破振動所包含的物理量

根據表1所列出的因變量及自變量可知，爆破振動波傳播過程主要涉及了10個變量，則變量總數n=10，其中取Q、R、c取為具有獨立量綱的物理量，即m=3，根據π定理，爆破振動速度的量綱分析問題中存在n-m=7個無量綱的變量，無量綱參數以π為代表：

(2)

式中：v、Q、R、c的單位制分別為LT-1、M、L、LT-1，根據π定理可知，為使等式兩邊成立，等式右側的分子分母的量綱需滿足齊次定理，則待定參數α、β、γ的值為α=0、β=0、γ=1，于是可以得出π=v/c。

同理，根據量綱齊次定理可以得出其余幾個無量綱參量為

(3)

通過化簡可以得出π1～π6分別為

(4)

由此可知爆破所引起的質點峰值振動速度與上述無量綱量存在一定的函數關系，其表達式如下[7]

(5)

對于特定的爆破環境，爆破振動波的傳播速度c及巖體的密度ρ均可視為常量，本文僅探討爆破振動與最大段藥量Q、爆源距R、高程差H及場地系數K之間的相互關系，故爆破所引起的質點振動峰值速度可以轉化為

(6)

考慮H/R與爆破振動波傳播與衰減間的相互關系，將等式兩端取對數得出

(7)

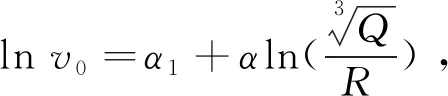
(8)

根據式(8)，令lnK1=α1，去掉等式兩邊的取對數符號可得

(9)

得出的是不考慮高程差情況下的質點振動峰值速度，也正是傳統的薩道夫斯基公式，故將式(9)帶入式(7)中，得出

(10)

假設lnK2=α2，則在考慮高程效應后，爆破振動峰值速度計算公式可以表達為

(11)

式中：K1為場地系數；K2為地形地貌影響系數；Q為爆破最大同段藥量；α為衰減系數；H為測點與爆源之間的高程差；R為爆源距，即爆源中心與測點的直線距離；β為高程影響系數。

2 工程應用

1)工程概況。該航運過壩工程位于廣西壯族自治區南寧市，處于該地區主要水系的核心部位，該工程是迎接廣西壯族自治區成立60周年的重點項目之一，建成后將成為該地區的一處綜合性水利樞紐工程。該航運過壩工程為單線單級2 000 t的船閘，設計水頭高度為8.38 m，輸水系統采用閘室底長廊道側支孔形式輸水。該工程主要包括上游引航道、船閘主體(包括進水口、跨船閘交通橋，上、下閘首、閘室)、下游引航道以及上、下游連接段航道、船舶侯閘錨地等，該工程軸線直線段總長約2.8 km。由于施工期間涉及規模較大的巖土開挖，且施工區域主要為巖質堅硬的灰巖，巖體結構相對完整，風化程度不高，土石方開挖量約為1 500 萬m3，采用傳統的機械開挖施工進度相對較慢、成本較高，不能滿足該工程施工進度的要求，故選用爆破技術進行巖土開挖作業[8]。

2)爆破參數及起爆網路。爆破施工區域采用深孔臺階爆破方式，炮孔直徑d取90 mm，藥卷直徑取70 mm，臺階爆破高度H取9 m，超深h取1 m，炮孔深度L取10 m，底盤抵抗線W0取3.5 m，孔距a取3.5 m，排距b取3 m，填塞長度l不小于3.5 m，單孔裝藥量Q為40 kg。

為了對比不同爆破器材的減振效果，共進行了兩次對比性爆破試驗，并采用不同的起爆網路，第1次采用孔外多孔間延時的導爆管雷管起爆網路，孔內采用高段位MS15段雷管進行延時，孔外采用低段位MS3段進行接力傳爆，每3發為一簇聯；第2次采用數碼電子雷管逐孔起爆網路，孔間延時50 ms[8]。

3)爆破振動監測。由于爆破區域周邊環境相對復雜，零散民房位于爆破區域的西北側，距離爆區中心最近僅有268 m，除此之外還有在建的船閘主體工程、壩體及護坡等附屬建(構)筑物，為了對爆區周邊的民用建筑、一期船閘主體工程及新澆筑的護坡進行保護，在爆破點附近設置了5處爆破振動監測點(見圖1)。

圖1 爆區周邊環境及爆破振動監測點布置
Fig.1 Layout of monitoring points for blasting vibration and surrounding environment in blasting area

3 高邊坡爆破振動傳播規律

1)爆破振動監測結果與分析。在5個需要被保護的建(構)筑物近爆區端各安裝上1臺中科院中科測控生產的爆破振動監測儀TC-4850，對各測點的爆破振動進行監測、記錄。為了真實的反映爆破所引起的建(構)筑物質點的振動速度，各監測點均采用石膏耦合劑將振動傳感器與地基貼合在一起，各測點的振動峰值速度如表2所示。

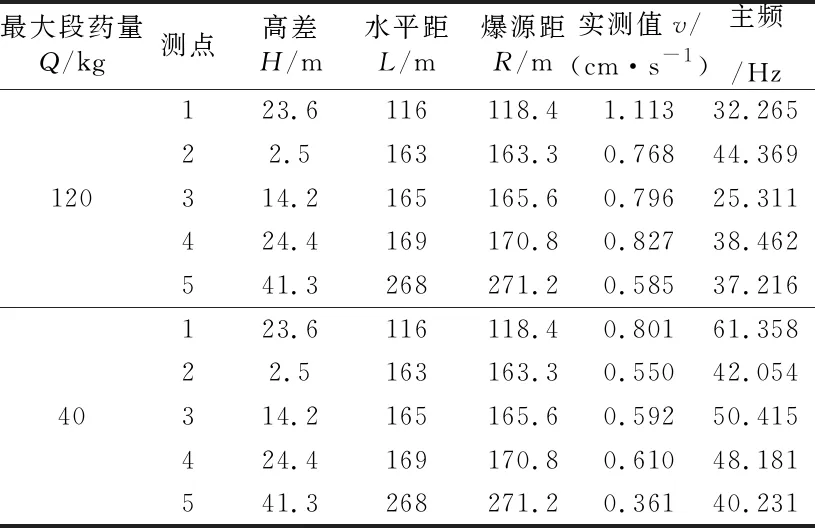
表2 各測點的峰值振動速度

由表2可知，最大段起爆藥量不同時，所對應的爆破峰值振動速度也有較大差別，最大段藥量越大，爆破所產生的質點振動峰值速度也就越大，減小最大段起爆藥量，爆破所產生的質點峰值振動速度也大大減小。通過多次爆破振動測試還可以發現，采用導爆管雷管進行爆破作業時，其所產生的爆破振動主頻大部分都小于采用數碼電子雷管的爆破振動主頻，根據《爆破安全規程》(GB 6722-2014)，頻率越高的爆破振動速度安全允許值越大[9]，故采用數碼電子雷管起爆網路在精確延時及提高爆破振動主頻上具有獨特的優勢。

2)爆破振動的非線性回歸分析。非線性回歸分析方法是利用已知數學模型中因變量與自變量之間的非線性關系，通過大量實驗數據依據牛頓迭代原理進行數據回歸，求解方程中的未知參數，進而獲得相應的具體表達式的一種科學研究方法[10]。

根據式(1)傳統的薩道夫斯基公式及式(11)考慮高程效應的爆破振動預測模型，采用表2的相關數據進行非線性回歸分析，通過回歸分析軟件，編寫相應代碼得出了兩種不同預測模型的預測值(見表3)，并得出了式(1)中的未知參數K為145.00，α為1.474；式(11)中的未知參數K1為143.65，K2為0.123，α為0.847，β為0.044；則采用式(1)進行非線性回歸得到的預測模型為

(12)

采用式(11)進行非線性回歸得到的預測模型為

(13)

表3 非線性回歸得到的PPV預測值

3)高邊坡爆破振動傳播規律。實際工程中一般采用爆破振動峰值速度來反映爆破振動的強度，根據表2所得到的爆破振動實測值及表3爆破振動速度預測值，通過比較5個對應監測點的爆破振動峰值速度結果，得到了實測值與采用式(12)、式(13)兩種不同預測模型所得到的預測值之間的關系(見圖2)。

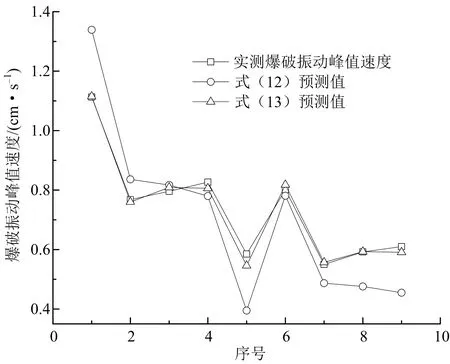
圖2 實測爆破振動峰值速度及預測值的對比
Fig.2 Comparison of measuredPPVand predicted values

由圖2可知，采用傳統的薩道夫斯基公式在高程差變化較為明顯的區域進行爆破振動預測時，其精度遠遠低于改進后的考慮高程效應的爆破振動預測模型。采用式(12)進行爆破振動預測時，其精度為83.48%，平均偏差為16.52%；采用式(13)進行爆破振動預測時，其精度為97.03%，平均偏差為2.97%，精度較高，說明采用改進后考慮高程效應的式(13)能較好的反映該地區爆破振動的傳播及衰減規律。

結合表2、表3(測點2～測點4)的實測數據及預測值可以得出：在水平距離L大致相同的情況下，高程越大的監測點所對應的爆破振動峰值速度越大，正高程對爆破振動具有一定的放大效應，但由于爆破振動波傳播過程中會有能量的消耗，該放大效應并非隨著高程的不斷增加而一直增加，當其增大到一定程度時，放大效應表現得不明顯，甚至表現為削弱效應。

4 爆破振動控制技術

無論是工程領域還是科學研究領域，爆破振動研究的最終目的均是分析其傳播衰減規律，并采取相應的技術措施來控制爆破振動的危害，進而減小爆破振動產生的負面效應。當前爆破振動控制技術主要分為3大類：爆破振動主動防護技術、被動防護技術、保護性防護技術。

1)爆破振動主動防護技術。主要是通過控制爆源能量的釋放，從根本上減小爆破振動效應。爆破工程實踐中，技術人員通常采用控制最大單段起爆藥量、合理調整延時時間、合理設置孔網參數等技術對爆破振動進行控制。近年來，數碼電子雷管憑借其精確的延時性能及有效提高爆破振動主頻的特征，在全國各地得到了廣泛的應用及推廣，大大減小了爆破振動的危害效應。

2)爆破振動被動防護技術。該類技術主要是通過傳播途徑削弱爆破振動波的能量，進而控制爆破振動有害效應。其主要的技術措施有，在爆區及被保護對象間開挖減振溝、采用預裂爆破技術及孔底空氣間隔技術等。相關研究表明，減振溝寬度越大、深度越深，控制爆破振動危害的能力就越強，預裂爆破技術及孔底空氣間隔裝藥技術也能在一定程度上削弱爆破振動的危害。

3)爆破振動保護性防護技術。此類技術主要是對被保護對象進行加固處理，以預防爆破振動對其產生較大的影響。但是，此技術實施成本較高，一般僅用于重點保護對象的爆破振動控制中。

5 結論

1)通過理論推導得出了反映高程效應的爆破振動預測模型，經實際工程驗證，得出了在具有明顯高程差的爆破區域，采用傳統的薩道夫斯基公式進行爆破振動預測時，其精度較低，平均偏差為16.52%。采用改進后反映高程效應的預測模型，其預測精度較高，達97.03%，能較好地反映該工程的爆破振動傳播及衰減規律。

2)通過數據對比可以得出：在水平距離L大致相同的情況下，正高程對爆破振動具有一定的放大效應，但該放大效應并非隨著高程的不斷增加而一直增加，當其增大到一定程度時，放大效應表現得不明顯，甚至表現出削弱效應。

3)兩次爆破作業時儀器所監測、記錄的爆破振動均小于2 cm/s，依照《爆破安全規程》(GB 6722-2014)中的規定[9]，該高邊坡的爆破施工不會對船閘壩體、新澆筑的護坡及測點所在民房造成較大的損傷。

4)減小最大單段起爆藥量能大大減弱爆破振動效應，數碼電子雷管的應用有助于削弱爆破振動危害，同時采用數碼電子雷管可以一定程度的提高爆破振動波的頻率，對保護建(構)筑物具有積極意義；同時，對于重要建(構)筑物保護，可在爆區及被保護建筑間開挖一條減振溝或鉆鑿一定數量的減振炮孔(不裝藥)，用于緩沖、釋放爆破振動波的能量，另外還可以采用預裂爆破技術、孔內空氣間隔裝藥減振技術對爆破振動進行預防、控制[11]，但實踐表明，單純采用某一種減振技術的減振效果并不理想，同類工程可采用綜合減振技術來控制爆破振動危害。