核電站中氣溶膠再懸浮的CFD研究

江 斌，黃 挺，陳 煉，常華健,2

(1.國核華清(北京)核電技術研發中心有限公司，北京 102209；2.清華大學 核能與新能源技術研究院，北京 100084)

壓水堆核電站在嚴重事故晚期時，由于可能出現的氫氣燃燒或爆燃等現象造成的瞬時氣流沖擊，會使得已沉積在安全殼壁面內的氣溶膠再次懸浮到氣空間中，導致安全殼氣空間內裂變產物濃度再次上升，從而可能導致放射性物質的再次釋放。由于氣溶膠再懸浮會對事故晚期放射性源項產生影響，最終影響釋放到環境中的放射性物質總量，因此有必要對該類現象進行深入研究。

已有用于反應堆嚴重事故評估的系統分析程序如ASTEC等[1]，根據不同原理開發了氣溶膠再懸浮機理的計算模型。但該類程序是集總參數程序，不能精細獲悉氣溶膠不同時刻粒子的位置分布等物理量，這不利于了解事故細節。

GASFLOW是一款用于模擬流體動力、傳熱傳質、化學反應、氣溶膠輸運與沉降及其他嚴重事故時反應堆內相關現象的CFD程序[3]。GASFLOW采用隱式連續歐拉-任意拉格朗日歐拉(ICE’d ALE)的方法求解三維可壓縮多組分的納維-斯托克斯方程，該方法屬于有限差分法，最初由Hirt等[4]提出，可適用于求解所有流速的計算流體力學問題。每個版本的GASFLOW都經過了國際上多項標準實驗的驗證，其計算結果也被多個亞洲和歐洲國家的權威機構所認可。拉格朗日方法描述了物質顆粒的運動，它是時間和空間的函數；歐拉方法描述了空間固定體積中的流動情況，求解其控制方程相對于拉格朗日方法更容易。ICE’d ALE方法能求解包括壓聲速和超聲速在內的所有流動問題，因為其具有與隱式連續歐拉法類似的隱式方程。其優勢包括可采用比顯式方法大得多的時間步長，以及能求解全拉格朗日方法無法求解的問題。控制方程可利用有限體積法在經典的交錯網格上求解，其中，流體的狀態量通過控制體中心網格求解，而速度矢量通過控制體面網格求解。由于采用了非貼體網格和亞網格技術，以及簡化的工程建模方法，使得GASFLOW在計算大型安全殼內的流場時具有很高的效率。

本文以GASFLOW3.3為基礎，對氣溶膠粒子進行受力分析，利用力學平衡原理建立氣溶膠再懸浮模型，并與國際標準例題ISP40的STORM試驗SR11[5]結果進行對比，在此基礎上對GASFLOW中再懸浮模型的改進提出合理化建議。

1 模型描述

根據經濟合作與發展組織(OECD)能源署[6]的有關定義，再懸浮是指由于流體流動的拖曳力，結構表面已經沉積的氣溶膠或凝聚物以細小碎片的形式懸浮起來。再懸浮也可由重新定位的熔體上注水產生的蒸汽尖峰或氫燃燒產生的流動所觸發。

目前，有關氣溶膠再懸浮的模型通常分為兩類，一類為力學平衡(FB)模型，另外一類為能量累積(EA)模型[7]。GASFLOW中用于模擬氣溶膠行為的模型包括拉格朗日粒子模型、隨機湍流粒子擴散模型、粒子沉降模型、粒子再懸浮模型及粒子云模型[8]。GASFLOW3.3采用了FB模型，對單一氣溶膠粒子進行受力分析，且為計算簡便，將粒子近似為球體。實際兩相流動中，經常采用基于體積的當量球半徑來計算粒子拖曳力[9]。圖1為穩定發展的湍流場中，沉積于壁面上的單一球形粒子的受力分析示意圖。

對于單一球形粒子，其受到的各力表達式如下。

(1)

(2)

(3)

(4)

(5)

Ff=fsFn=fs(Fg+Fa-Fb-Fl)

(6)

目前，我國所開發利用的鉬資源一般來自單一鉬礦石類型、銅鉬礦石類型和鎢鉬礦石類型等。從以鐵為主的鐵鉬型礦石中回收鉬的生產實踐尚不多見。本技術為從鐵鉬型礦石中回收鉬提供了一條切實可行的技術路線，對處理同類型性質礦石具有很大的借鑒價值，具有較好的推廣前景。

圖1 穩定且完全發展的湍流場中單一球形粒子的受力Fig.1 Force acting on single spherical particle with steady and fully developed turbulent flow

此外，流體中的粒子通常還會受到壓力梯度力、虛擬質量力、Basset力、Magnus力、Saffman力和熱泳力等作用。盡管作用在粒子上的力十分復雜，但在氣溶膠懸浮體系中，由于氣體的密度通常遠小于粒子的密度，與粒子本身慣性相比，浮力、壓力梯度力和虛擬質量力等均很小，可忽略不計[12]。在以上兩相間的相互作用力中，拖曳力是十分重要的力，它是對兩相間的相對流動、傳熱和傳質等起著重要作用的力。根據Evett等[13]的公式可計算出拖曳力。

上述受力中，重力、浮力和黏性力僅取決于粒子和氣體的物理性質，與氣流速度無關。主要的黏性力是范德瓦爾斯力、靜電力和其他黏性力。這些力主要受到下列因素的影響：粒子的材料、形狀和尺寸，表面的材料、粗糙度和污染程度；環境氣體的相對濕度和溫度；粒子-表面接觸的持續時間和初始接觸速度。而拖曳力和升力取決于氣流速度且隨氣流速度的增大而增大。當氣流速度增大到一定程度，拖曳力等于靜摩擦力時，氣溶膠粒子開始運動并離開沉積表面，此時：

Fd=fs(Fg+Fa-Fb-Fl)

(7)

將式(1)～(5)代入式(7)中，可得：

(8)

式(8)是以Ugcp為未知數的方程，通過求解該方程可得出單一粒子的最小懸浮速度，將其用Ugcp0表示。當氣流速度大于該速度時，氣溶膠粒子就可懸浮起來。

2 幾何建模及計算條件

2.1 幾何建模

STORM試驗臺架位于意大利的Ispra，是由聯合研究中心JRC運行維護的。STORM試驗SR11分為兩個獨立階段，第1階段集中在氣溶膠粒子由于熱泳和湍流影響導致的沉積現象，第2階段關注的是已沉積的氣溶膠粒子在逐步增加的氣流下導致的再懸浮現象。

GASFLOW是一個適合于大尺度、安全殼內的工程CFD程序，對于細長小管徑是否適用需進一步研究。為便于對模型適用性進行分析，利用GASFLOW建立一長方形管道模型，其方形管口尺寸為0.5 m×0.5 m，長度為5.005 5 m，初始條件與SR11設置完全一致。設定初始狀態下氣溶膠的沉積區域如圖2所示。

在保證氣溶膠充分沉積后，在管口處設定一持續1 s的速度邊界，使管內產生一水平方向的流場，該風流將使沉積的氣溶膠產生再懸浮，再懸浮率η的計算公式為：

(9)

其中：N0為初始狀態下沉積在表面的氣溶膠顆粒數量；Nr為氣流停止時沉積在表面的氣溶膠顆粒數量。

圖2 氣溶膠初始沉積區域示意圖Fig.2 Schematic diagram of aerosol initial deposition area

2.2 初始條件

表1列出計算分析的初始條件。其中邊界層厚度、拖曳力系數粗糙度因子和顆粒與沉積表面的平衡間距粗糙度因子是GASFLOW3.3中與再懸浮模型相關的3個主要輸入參數。核電站在嚴重事故條件下，安全殼內氣溶膠粒子中包含了各種核素成分，粒徑的典型值為1.0 μm[14]，因此本文選取該典型直徑進行分析。

表1 計算的初始條件Table 1 Initial condition for calculation

由于氣溶膠粒子運動具有隨機性，因此數目越多的粒子數量越能更好地反映再懸浮的隨機特性。但太多粒子數量會占用大量的計算資源，因此需對初始氣溶膠粒子的數量進行合理選定。

圖3示出在表1設定的初始條件下，氣溶膠再懸浮率隨氣溶膠粒子數量的變化。由圖3可看出，當氣溶膠粒子數量大于等于1×105時，氣溶膠再懸浮率的計算結果基本保持不變，因此選定氣溶膠粒子數量為1×105個進行后續的分析計算。

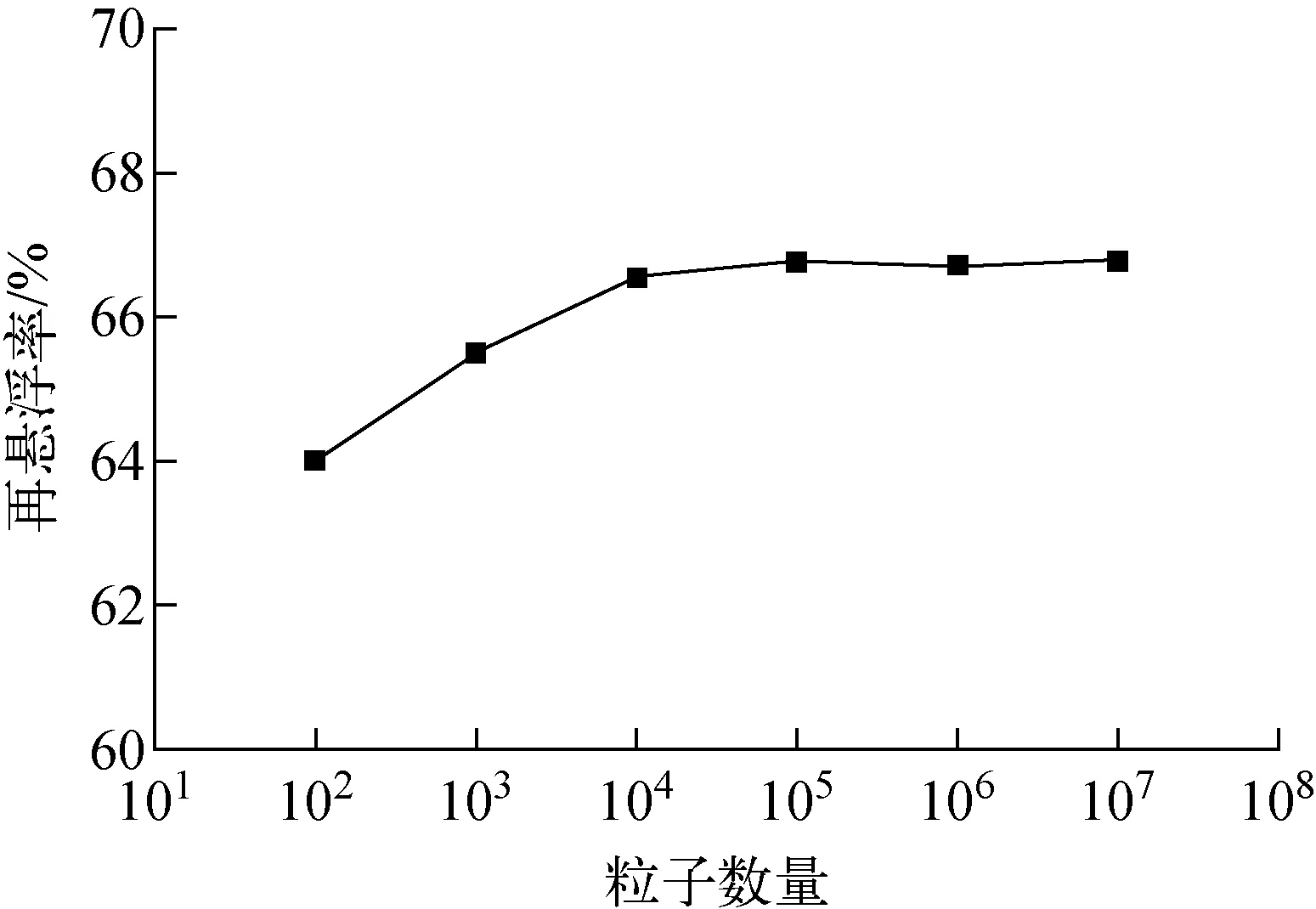
圖3 不同氣溶膠粒子數量的再懸浮率Fig.3 Resuspension rate for different aerosol particle numbers

GASFLOW是利用拉格朗日粒子追蹤法進行計算分析的，為計算的簡便，同時在工程角度適用的情況下，不考慮粒子間的相互作用，且粒子與流場間的作用和傳熱微乎其微，因此也不予考慮。

3 計算結果及分析

3.1 再懸浮率

圖4示出STORM試驗SR11的結果及ASTEC和GASFLOW程序的計算結果。其中FB-1、FB-2、RNR-1和RNR-2分別代表ASTEC程序中SOPHAEROS模塊采用的兩種不同模型計算的結果。FB-1和FB-2均采用FB模型，區別在于FB-1的黏性力系數為1.0×10-6N/m，FB-2的黏性力系數為1.0×10-5N/m。RNR-1和RNR-2均采用EA模型，區別在于RNR-1的最大時間步長為1.0 s，RNR-2的最大時間步長為30.0 s。GASFLOW-1和GASFLOW-2采用的是FB模型，區別在于GASFLOW-1的楊氏模量為2.1×1012dynes/cm2, GASFLOW-2的楊氏模量為2.1×1013dynes/cm2。從圖4可看出，GASFLOW與ASTEC程序的計算結果有所不同，這是由于兩者采用的是不同模型，且圖5示出兩個不同時刻氣溶膠粒子的位置分布。由圖5可看出，距流場越近再懸浮粒子的數量越多，這是由于距流場不同，所受到的升力大小也不同。

圖4 再懸浮率試驗與計算結果的對比Fig.4 Comparison of resuspension rate between test and calculated results

ASTEC是集總參數程序，GASFLOW是CFD程序，因此計算結果有所差別。GASFLOW-1和GASFLOW-2的計算結果也有所差別，這是由于兩者的楊氏模量不同，因而導致兩者的黏性力不同，再懸浮率也不同，這一結論與FB-1和FB-2的計算結果不同是一致的，說明黏性力是影響再懸浮率的一個重要因素。同時還可看出，GASFLOW-1和GASFLOW-2與試驗結果SR11的差距在20%以內，在工程應用范圍內符合較好，GASFLOW能較好模擬氣溶膠的行為，可在工程應用中提供參考。

3.2 位置分布

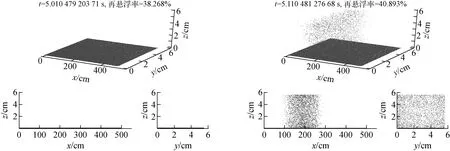
圖5 不同時刻氣溶膠的位置分布Fig.5 Position distribution of aerosol at different time

圖6 氣溶膠再懸浮率隨時間的變化Fig.6 Change of aerosol resuspension rate with time

圖6示出氣溶膠再懸浮率隨時間變化的定量分析。由圖6可看出，氣溶膠的再懸浮是一瞬態過程，再懸浮率隨時間的變化是一階梯狀的過程。

4 結論

研究結果表明，GASFLOW3.3中的再懸浮模型基本可用來模擬核電站中氣溶膠的再懸浮行為，根據計算結果可得到以下結論。

1) GASFLOW與ASTEC程序的計算結果有所區別，黏性力是影響再懸浮率的一個重要因素。

2) 氣溶膠的再懸浮是一瞬態過程，再懸浮率隨時間的變化是一階梯狀的過程。只要已沉積的氣溶膠粒子最小懸浮速度小于氣流速度，氣溶膠粒子就可懸浮。

3) 由計算結果可看出，GASFLOW作為一個CFD程序，計算結果與SR11試驗結果的差距在20%以內，在工程范圍內是可接受的。GASFLOW能較好模擬氣溶膠的行為，并展示不同時刻氣溶膠粒子位置的分布，可為工程應用提供參考。

4) 氣溶膠再懸浮現象是安全殼內嚴重事故晚期的一個重要現象，從試驗結果和兩個程序計算的結果可看出，均有超過50%的氣溶膠粒子在嚴重事故晚期發生再懸浮，這一比例對于源項的影響很大，在源項分析中需多加關注。同時，更加合理精確的氣溶膠再懸浮模型有待進一步開發。