H13熱作模具鋼熱- 機械疲勞損傷和壽命的預測

張永強 徐國財 左鵬鵬 黎軍頑 吳曉春

(1. 大冶特殊鋼有限公司, 湖北 黃石 435001; 2. 上海大學材料科學與工程學院, 上海 200444;3. 省部共建高品質特殊鋼冶金與制備國家重點實驗室, 上海 200444)

H13熱作模具鋼具有良好的強度和韌性，被廣泛用于制作壓鑄、擠出和鍛造模具，由于使用條件嚴酷，模具會發生不同形式的失效[1]。例如，在壓鑄過程中，與金屬液直接接觸的模具表面同時受到熱和應力的強烈作用，會使模具因熱疲勞和溶蝕而失效[2]；在熱擠壓過程中，模具除了承受長時間的熱作用外還承受不斷增大的機械載荷[3]，紅熱金屬與模具產生嚴重的摩擦熱，導致模具磨損[4]；在熱鍛過程中，模具拐角處往往會產生應力集中，從而過早出現微裂紋，導致模具斷裂[5]。熱作模具在使用中不僅受到熱的作用，還承受較大的外加載荷，僅將模具的失效歸因于熱疲勞是片面的，因此研究人員開始嘗試將用于研究高溫合金失效的熱- 機械疲勞(thermo- mechanical fatigue, TMF)試驗應用于H13鋼熱作模具的失效分析。例如，方健儒等[6]研究了熱作模具鋼在控制應力幅條件下的等溫疲勞和同相位 (in- phase, IP) 的熱- 機械疲勞壽命，發現，應力幅相同，同相(IP)熱- 機械疲勞壽命低于上限溫度的等溫疲勞壽命；Chen等[7]基于連續損傷模型研究了H13鋼在疲勞- 蠕變交互作用下的損傷行為，并通過500 ℃等溫疲勞和疲勞- 蠕變試驗進行驗證，指出采用疲勞- 蠕變循環中累積塑性應變描述損傷更為合理；左鵬鵬等[8]基于應變控制的熱- 機械疲勞試驗，研究了4Cr5MoSiV1鋼的同相(IP)和反相(out- of- phase, OP)熱- 機械疲勞滯后回線的變化，認為材料的微觀組織(含高密度位錯的板條馬氏體和彌散分布的碳化物)隨循環次數的增加而發生循環軟化，并對其熱- 機械疲勞壽命進行了預測。

本文根據ASTM E2368- 10熱- 機械疲勞試驗標準[9]，采用MTS熱- 機械疲勞試驗機對H13熱作模具鋼在200～600 ℃、機械應變為0.7%和0.9%的條件下進行了熱- 機械疲勞試驗，根據循環損傷理論分析了鋼的熱- 機械疲勞損傷，并結合唯象壽命模型預測了鋼的熱- 機械疲勞壽命。

1 試驗材料與過程

1.1 試樣

試驗用H13鋼采用電爐熔煉并經電渣重熔，化學成分如表1所示。熱處理工藝：在真空爐中1 030 ℃奧氏體化30 min油淬，隨后590 ℃×2 h回火2次，硬度為(46±1.0) HRC。熱- 機械疲勞試驗試樣的幾何尺寸如圖1所示。

表1 試驗用H13鋼的化學成分(質量分數)Table 1 Chemical composition of the investigated H13 steel (mass fraction) %

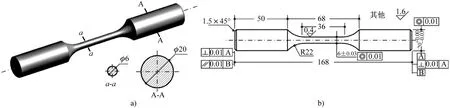
圖1 熱- 機械疲勞試驗試樣Fig.1 Thermo- mechanical fatigue test specimen

1.2 試驗過程

按ASTM E2368- 10熱- 機械疲試驗標準要求，采用MTS Landmark 370.10型熱- 機械疲勞試驗機對H13鋼進行熱- 機械疲勞試驗。試樣標距為12 mm，感應加熱，冷卻介質為壓縮空氣。在熱- 機械試驗加載中，總應變(εTot)與機械應變(εM)和熱應變(εTh)之間的關系如式(1)和式(2)所示：

εTot=εM+εTh

(1)

εTh=α(T-T0)

(2)

式中：α為熱膨脹系數，T為試樣溫度，T0為參考溫度。采用式(2)標定熱應變，熱膨脹系數α為1.49×10-5/℃。采用典型的同相位(φ=0°, IP)和反相位(φ=180°, OP)兩種載荷模式進行試驗，如圖2所示。試驗溫度為200～600 ℃，參考溫度為400 ℃，機械應變為0.7%和0.9%，應變比R為-1，循環周期為200 s，試驗至試樣斷裂。

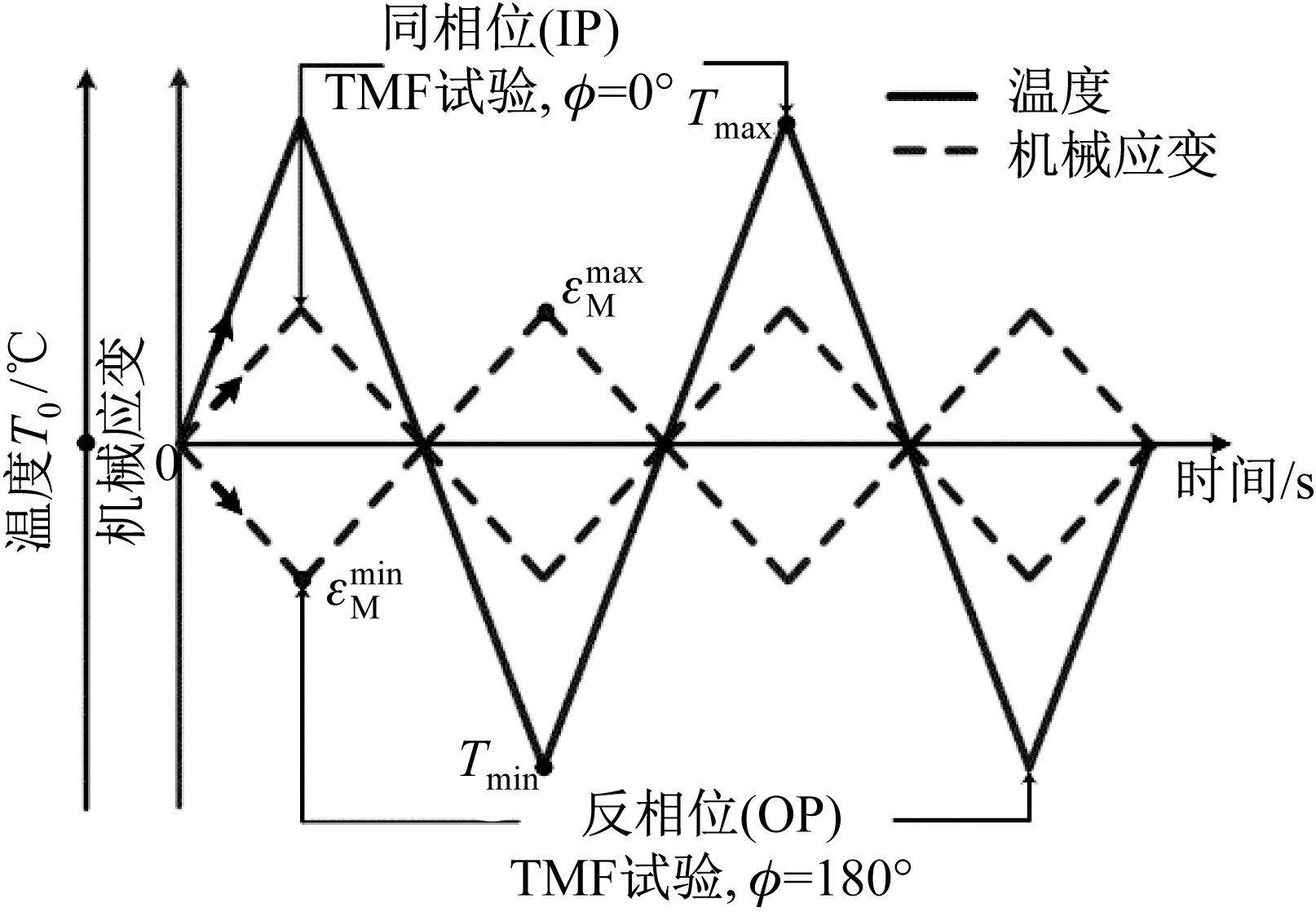
圖2 同相(IP)和反相(OP)熱- 機械疲勞試驗示意圖Fig.2 Schematic of in- phase (IP) and out- of- phase (OP) thermo- mechanical fatigue tests

2 結果與分析

2.1 應力- 應變響應行為

圖3是機械應變為0.7%和0.9%，在同相(IP)和反相(OP)加載條件下第一、第二和半壽命周期的應力- 應變響應曲線。同相(IP)加載時，溫度和機械應變同時達到最大或最小值，反相(OP)加載則相反。盡管加載過程中機械應變保持良好的對稱性，但無論是在同相(IP)還是反相(OP)加載情況下，試樣的最大拉應力和最大壓應力都顯示出了明顯的不對稱性，并且這種應力的不對稱出現在每一個熱- 機械循環中，這與H13鋼在不同溫度的抗拉強度和楊氏模量密切相關。在相同的應變載荷下，低溫(200 ℃)時材料的形變抗力較大，所需的應力也較大，應力- 應變響應曲線表現出明顯的加工硬化和應力松弛。同相(IP)加載時，隨著循環次數的增加，材料每個循環周發生的塑性應變也隨之增大；在反相(OP)加載時，對應循環周的塑性應變大致相當。機械應變的增加使對應循環周的塑性應變明顯增大，導致材料的損傷加劇，高溫和低溫半周材料都產生塑性應變，高溫半周明顯大于低溫半周。

圖3 第一、二和半壽命周時H13鋼的應力- 應變曲線Fig.3 Stress- strain curves at the time of first, second and half life cycles for H13 steel

2.2 循環損傷

張哲峰等[10- 11]在研究材料的低周疲勞時提出以能量作為主要損傷參量的滯回能模型，并建立了循環滯回能與損傷參數之間的關系：

(3)

式中：Di和Wi分別為第i周的損傷參數和滯回能；W0和β為材料常數，W0被定義為材料的本征疲勞韌度，β為損傷轉化指數。根據上述模型，當損傷參數疊加得到的D值達到1時材料就發生破壞。如圖4所示，第i周的滯回能Wi與該周的應力和應變范圍存在如下線性關系：

(4)

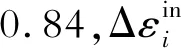
圖5表示H13鋼試樣滯回能隨熱- 機械循環周次的變化。由圖5可知，滯回能隨熱- 機械循環次數的增加而增加，到達一定的循環周次后突降，試樣經歷了明顯的損傷累積和疲勞失效過程。不同循環次數時的應力- 應變響應曲線的形狀由“細長形”向“扁平形”轉變，最后呈完全不同于正常循環的畸形。在相同的機械應變條件下，不同相位加載時，相同的循環次數對應的滯回能大小略有差異，同相(IP)熱- 機械疲勞稍大于反相(OP)熱- 機械疲勞。例如，機械應變為0.7%、熱- 機械循環200周次時，同相(IP)熱- 機械疲勞的滯回能為7.434 4 MJ/m3，反相(OP)熱- 機械疲勞的滯回能為6.908 8 MJ/m3。當溫度和機械應變相位相同時，機械應變越大，對應的滯回能也越大。例如，機械應變為0.7%和0.9%、熱- 機械循環200周次時，同相(IP)熱- 機械疲勞的滯回能分別為7.434 4和11.726 6 MJ/m3，兩者相差約4.292 2 MJ/m3。反相(OP)熱- 機械疲勞的情況也相同。滯回能不僅局限于其數值的大小，更重要的是其與疲勞壽命的關系，當滯回能曲線從“水平”轉變為“豎直”時，該區間對應的循環周次近似地反映了H13鋼的熱- 機械疲勞壽命。

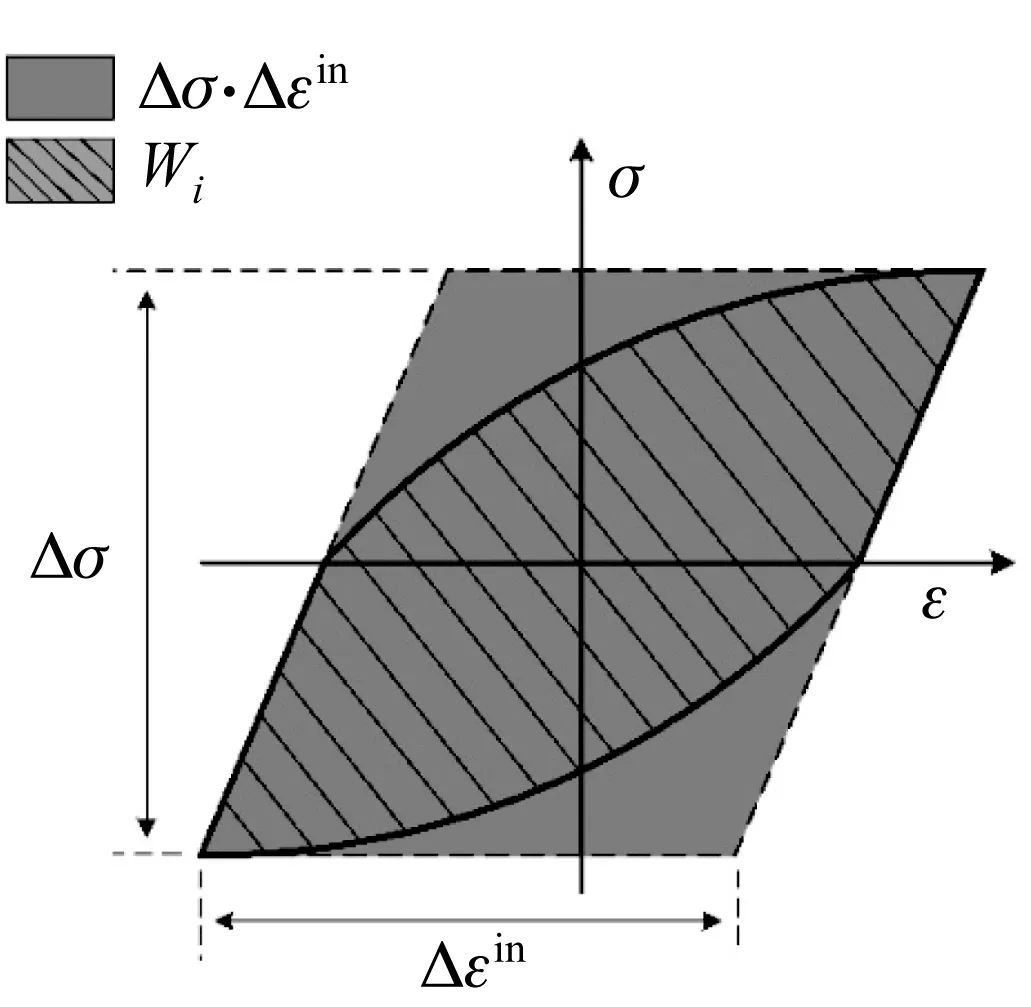
圖4 滯回能與應力- 應變范圍的關系Fig.4 Relation of the hysteresis energy to the stress- strain range

圖5 熱- 機械疲勞過程中H13鋼試樣滯回能隨循環次數的變化Fig.5 Variation of the hysteresis energy with the number of cycles during the thermo- mechanical fatigue test for H13 steel specimens

2.3 疲勞壽命

由于熱- 機械疲勞的復雜性，迄今未有統一的模型能準確預測材料的熱- 機械疲勞壽命。在熱- 機械疲勞壽命預測模型中，基于能量建立的拉伸遲滯能(Ostergren)模型[12- 13]被認為較適合于預測熱- 機械疲勞壽命。Ostergren模型采用凈拉伸滯后能(σtmax·Δεin)表征疲勞損傷，認為材料的疲勞壽命主要是非彈性應變和循環拉應力共同作用的結果，其數學模型為：

(σtmax·Δεin)·Nfm=C

(5)

式中：σtmax為最大拉應力，Δεin為非彈性應變范圍，Nf為斷裂時的循環周次，m和C為材料常數。該模型中應力和應變參數取自半壽命周期應力- 應變響應曲線。由此建立的H13鋼的同相(IP)和反相(OP)熱- 機械疲勞壽命的預測模型如下：

IP- TMF:

(σtmax·Δεin)·Nf1.098 4=1 672.553 43

(6)

OP- TMF:

(σtmax·Δεin)·Nf1.124 68=3 404.709 0

(7)

試驗測定和預測的機械應變為0.7%和0.9%時H13鋼的熱- 機械疲勞壽命如圖6所示。圖6中表明：(1) 機械應變相同，鋼的同相(IP)與反相(OP)熱- 機械疲勞壽命稍有差異，前者略大于后者；(2) 相位相同，隨著機械應變的增大，鋼的熱- 機械疲勞壽命明顯降低。例如，實測的機械應變為0.7%和0.9%的同相(IP)熱- 機械疲勞壽命分別為287和207周次，后者下降了約27.9%；(3) 根據Ostergren壽命預測模型預測的機械應變為0.7%和0.9%的同相(IP)和反相(OP)熱- 機械疲勞壽命分別為323、313周次和198、194周次，實測和預測的同相(IP)和反相(OP)熱- 機械疲勞壽命均比較吻合。

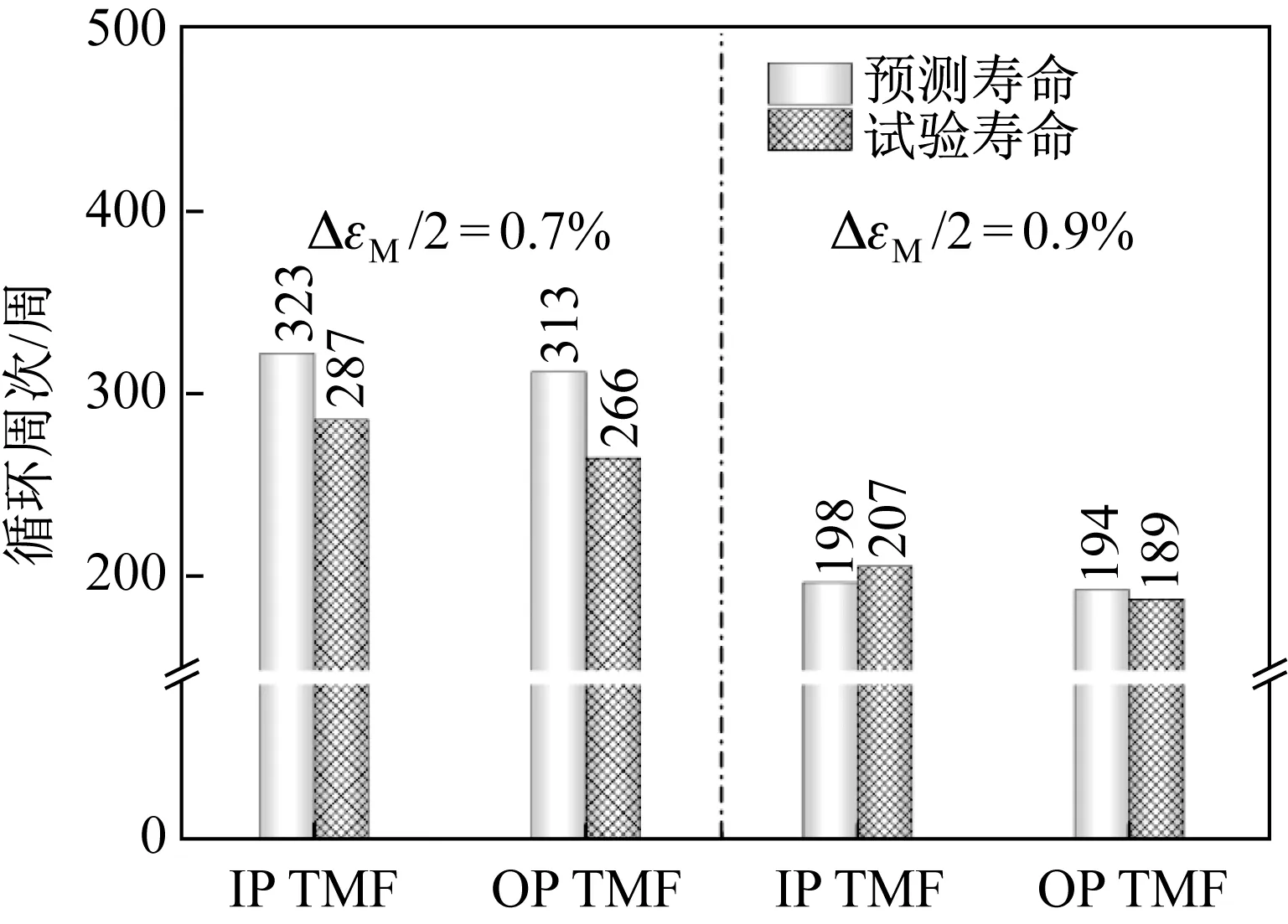
圖6 試驗測定和預測的H13鋼的熱- 機械疲勞壽命Fig.6 Thermo- mechanical fatigue lives of H13 steel obtained from the test and the prediction

3 結論

(1)在同相(IP)和反相(OP)熱- 機械疲勞過程中，盡管機械應變保持了良好的對稱性，但應力- 應變響應曲線明顯不對稱。隨著機械應變的增大，材料的損傷加劇，在應力- 應變響應曲線的高溫和低溫半周均產生塑性應變，且高溫半周明顯大于低溫半周。

(2)熱- 機械循環過程中，滯回能隨循環次數的增加而增大，達到一定的循環周次后出現突降，應力- 應變響應曲線從細長形轉變為扁平形，最后呈完全不同于正常循環時的畸形，H13鋼經歷了明顯的損傷積累和疲勞失效過程。

(3)機械應變為0.7%的H13鋼，根據Ostergren壽命模型預測的同相(IP)和反相(OP)熱- 機械疲勞壽命分別為323和313周次，而機械應變為0.9%的H13鋼，預測的同相(IP)和反相(OP)熱- 機械疲勞壽命分別為198和194周次，預測壽命與實測結果均較吻合。