基于概率包絡的輪對軸承故障診斷方法

丁家滿，原 琦，李 川

(昆明理工大學 信息工程與自動化學院，云南 昆明 650500)

在城市軌道交通迅速發展的今天，輪對軸承作為列車運行的核心部件，因為長期處在高速運轉的工作環境下，導致輪對軸承極易產生損壞。在列車高速運行情況下，一旦軸承發生故障將造成車輛延誤，若對故障發現不及時并且沒有采取相應有效措施，容易引起重大事故，甚至造成嚴重人員傷亡。因此，開展列車輪對軸承狀態監測和故障診斷方面的研究尤為重要，而且十分必要[1-3]。

常見的列車輪對軸承狀態監測與故障診斷方法有共振解調方法、沖擊脈沖方法、小波分析等[4-6]，這些方法在早期輪對軸承故障診斷中應用較為廣泛，在單一故障診斷方面取得較好的診斷效果，近些年涌現出了諸如基于模糊理論、知識推理、遺傳算法和人工神經網絡等具有智能特點的故障診斷方法[7-11]。文獻[12]采用高斯RBF神經網絡建立智能故障診斷系統用于機械齒輪箱故障診斷。文獻[13]結合小波分解和集合經驗模態分解來提取信號故障特征，利用能量判別法和搜索算法進行故障模式識別。文獻[14]利用局部均值分解對信號進行分解，從中提取時域統計量和能量等特征參數作為神經網絡的輸入參數，訓練故障診斷模型。然而，在現實中，隨著輪對軸承之間的耦合性越來越高，造成故障的原因大多數是多重原因，輪對軸承信號的采集也是多方面的，采集到的故障信號信息也存在不確定性，即便符合某種分布，很可能也存在波動情況。例如軸承振動信號基本符合正態分布，但信號均值在[a,b]之間，方差在[c,d]之間漂移。另外，在對原始信號進行特征提取會帶來特征以外的信息缺失問題。對于這種情況，采用傳統方法，簡單使用分布函數來代替或者用區間來表達都不合適，都存在無法完整描述、信息丟失的問題。

針對上述問題，本文引入概率包絡理論，以SVM為分類模型，提出一種基于概率包絡的輪對軸承故障診斷方法(PE-SVM)。在對原始輪對軸承信號分布類型檢驗的基礎上，建立概率包絡模型，提取其幾何形狀特征作為SVM的輸入，訓練并得到診斷模型。診斷結果表明該方法較好地包容了輪對軸承故障診斷中存在的不確定性問題，提高了診斷精度。

1 概率包絡基礎理論

1.1 概率包絡定義

概率包絡(Probability Envelope，PE)結合概率論和區間理論，通過計算隨機變量的累計概率函數(Cumulative Probability Distribution Function,CDF)積分面積變化范圍，將不確定性變量的波動漂移包裹在一個具有上下邊界的區域內，防止信息丟失。概率包絡同時考慮了不確定參數固有的隨機性和不精確性。

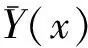
(1)

(2)

則CDF函數的范圍為PE，可表示為

(3)

利用PE將變量X的累積概率函數限制在一個范圍內，即有

(4)

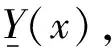
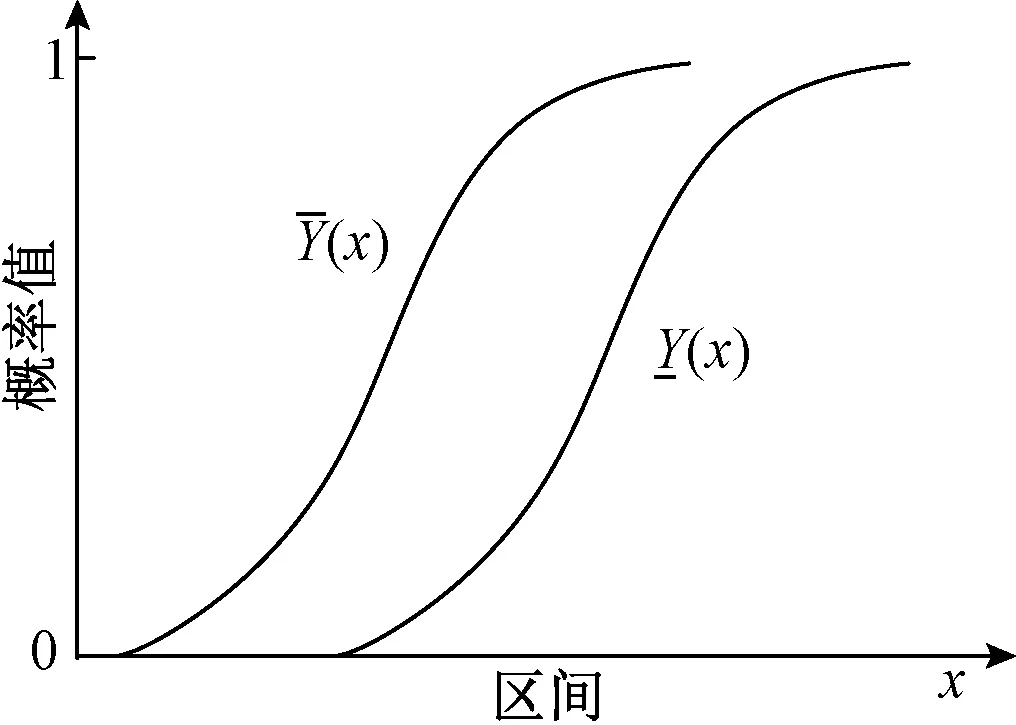
圖1 概率包絡示意

1.2 證據結構體

證據結構體(Dempster-Shafer Structure,DSS)由有限個焦元組成，每個焦元由一個區間和區間信度組成，即

{([x1,y1],m1),([x2,y2],m2),…,([xn,yn],mn)}

所有焦元對應的信度之和為1，即∑mi=1。

假若樣本空間為R，則處于這個鄰域R的證據結構體m即mass函數可以表示為

2R→[0,1]

則置信函數為

(5)

似然函數為

(6)

1.3 概率包絡與證據結構體

概率包絡的核心是由多個DSS構成，與證據結構體之間可以相互轉化。

由DSS可以繪制出概率包絡下邊界為

(7)

概率包絡上邊界為

(8)

如果將概率包絡看成整體，那么證據結構體就是它的組成部分。將所有證據結構體xi值按mi間隙縱向排列并將其連接成線可以得到概率包絡上邊界。同理，將所有證據結構體yi值按mi間隙縱向排列并將其連接成線可以得到概率包絡下邊界。反之，將概率包絡水平均勻切成n片，可以近似得到多個證據結構體，切線兩個端點組成證據結構體的區間，切片的高度為其信度(均勻切片，故所有證據結構體的信度相等，為n分之一)，如圖2所示。

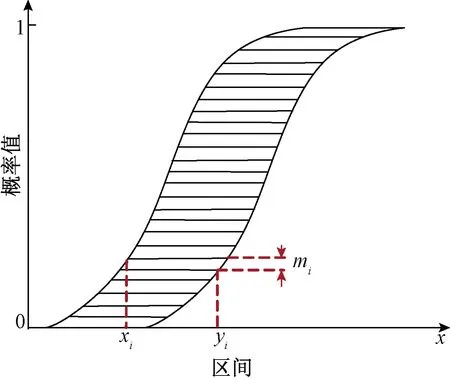
圖2 概率盒的等信度離散化

2 基于概率包絡的輪對軸承診斷方法

2.1 概率包絡建模

針對故障信號出現的各類不確定性問題，利用概率包絡建模將采集到的不確定信號繪制在一個包絡結構體內。在分析軸承故障信號分布特點的基礎上，采用3種建模方法，其建模過程分為以下幾個步驟：

step1對采集到的原始信號進行時頻域概率分布比對，判斷其分布類型。

step2若原始信號基本遵循某種概率分布規律，則利用原始參數概率包絡建模方法(the Probability Envelope Modeling Method Based on Original Parameters,OPPEM)進行概率包絡建模。

step3若原始信號不遵循某種概率分布規律時，提取其無量綱特征并分析其分布特點，判斷是否遵循某種概率分布規律，若滿足則采用特征參數概率包絡建模方法(the Probability Envelope Modeling Method Based on Characteristic Parameters,CPPEM)。

step4若所提取的特征信息無法確定概率分布類型時，則采用概率包絡定義建模方法(the Probability Envelope Modeling Method Based on Definition,DPEM)。

建模流程如圖3所示。

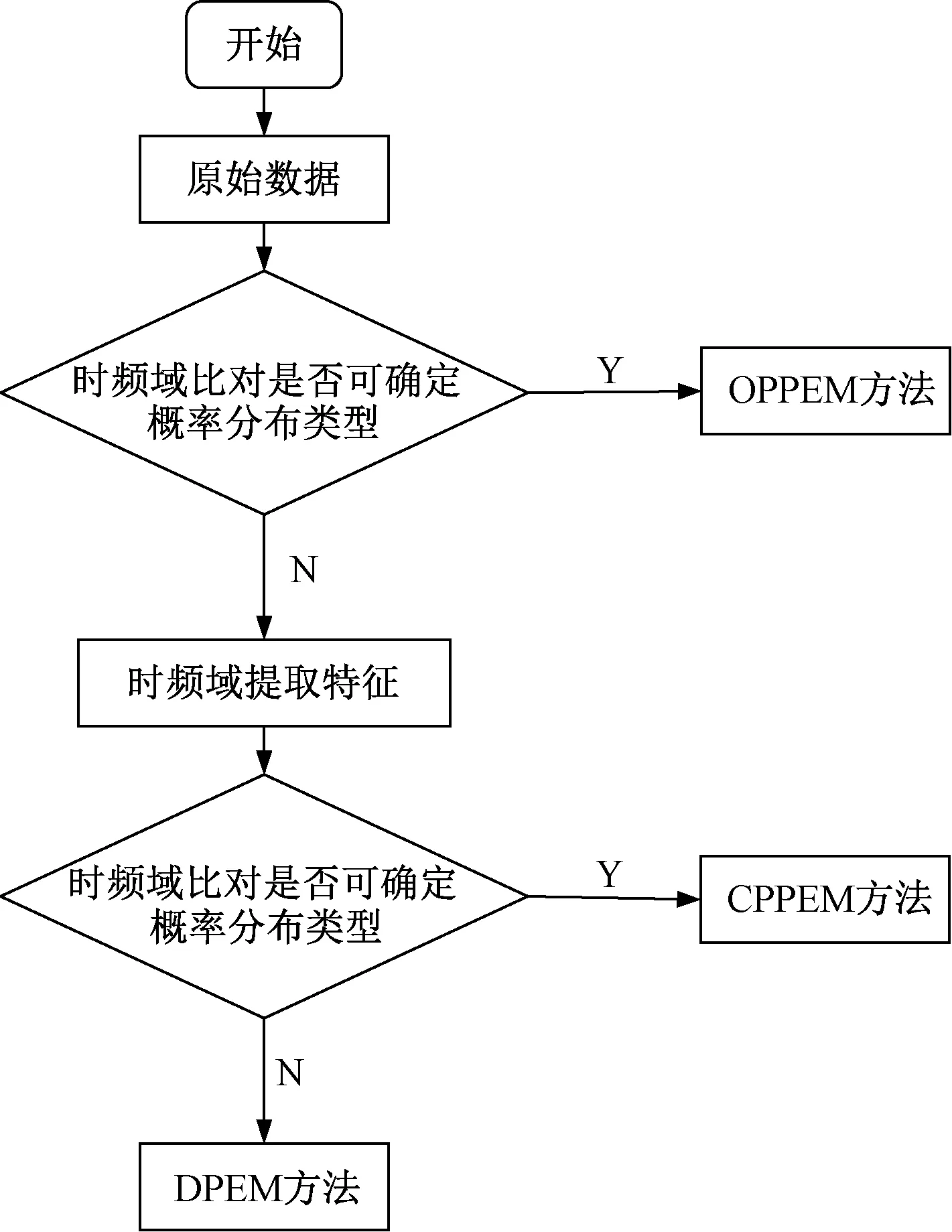
圖3 建模流程

2.2 概率包絡特征提取

在針對不同的分布采用不同的建模方法對信號進行概率包絡建模后，提取出概率包絡的特征量作為后續診斷的特征不僅可以增加診斷精度而且可以降低因為數據規模增大帶來的時間消耗問題。本文通過提取概率包絡的幾何形狀構成特征向量。

(1)累積包絡寬度

累積包絡寬度主要是為了描述信號數據的不確定的范圍，其計算公式為

(9)

(2)對數累積包絡寬度

其本質是對累積包絡寬度取對數運算，在壓縮不確定范圍的同時，消除模型的異方差等特性，其計算公式為

(10)

(3)累積區間寬度

累積區間寬度主要是為了描述不確定性信號的取值平均范圍，其計算公式為

(11)

(4)邊界值

其本質是獲取PE的累積置信區間，即PE上下界的各自加和，計算公式為

(12)

(5)矛盾區間統計

矛盾區間統計本質是計算DSS的上界值大于下界值的特殊信號點的個數，其計算公式為

(13)

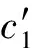
(6)權重區間

其本質是計算對數累積包絡寬度之外的焦元權重區間，其計算公式為

(14)

2.3 基于概率包絡的故障診斷

基于概率包絡的故障診斷方法的主要思想是將提取到的概率包絡的幾何形狀作為特征向量輸入到支持向量機SVM，訓練得到分類器，進行故障診斷。

基于概率包絡故障診斷算法如下：

Input: 信號數據{x1,x2,…,xm}

Output: 故障分類診斷結果

Step1forn=1 tom

Step2概率包絡建模

Step3提取特征向量{y1,y2,…,yn}

Step4end

Step5將特征數據切分為訓練集{a1,a2,…as}和測試集{b1,b2,…bt}

Step6初始化參數K(K折交叉驗證)

Step7forj=1 toK

Step8選取徑向核函數

Step9確定參數懲罰因子C和σ

Step10end

Step11fori=1 toS

Step12確定松弛變量和權重系數:ε，w

Step13訓練模型

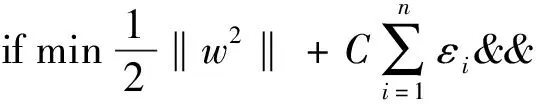
yi(wTxi+b)≥1-εi(i=1,2,…,n;εi≥0)

Step14end

Step15測試數據測試模型得出分類精度

3 實驗結果與分析

本文分別選用了公共數據集和實測數據進行了3次實驗，實驗一主要驗證本文提出基于概率包絡的特征提取方法的有效性，實驗二和實驗三分別從公共數據集和實測數據進一步說明本文方法的有效性及泛化能力。其中滾動軸承振動數據選用NSFI/UCR智能維護系統中心的公共數據集(IMS-www.imscenter.net)。實驗裝置如圖4所示,其中安裝了4個軸承，旋轉速度為2 000 r/min，采樣頻率為1 024 Hz，軸和軸承上施加了6 000磅(約2.78 kN)的徑向載荷。

圖4 軸承故障測試實驗裝置

本實驗選取數據集1中的第三個軸承的數據，其中正常與內圈故障數據各60 000條。

對原始信號進行頻譜分析，其時域波形和頻譜如圖5所示。

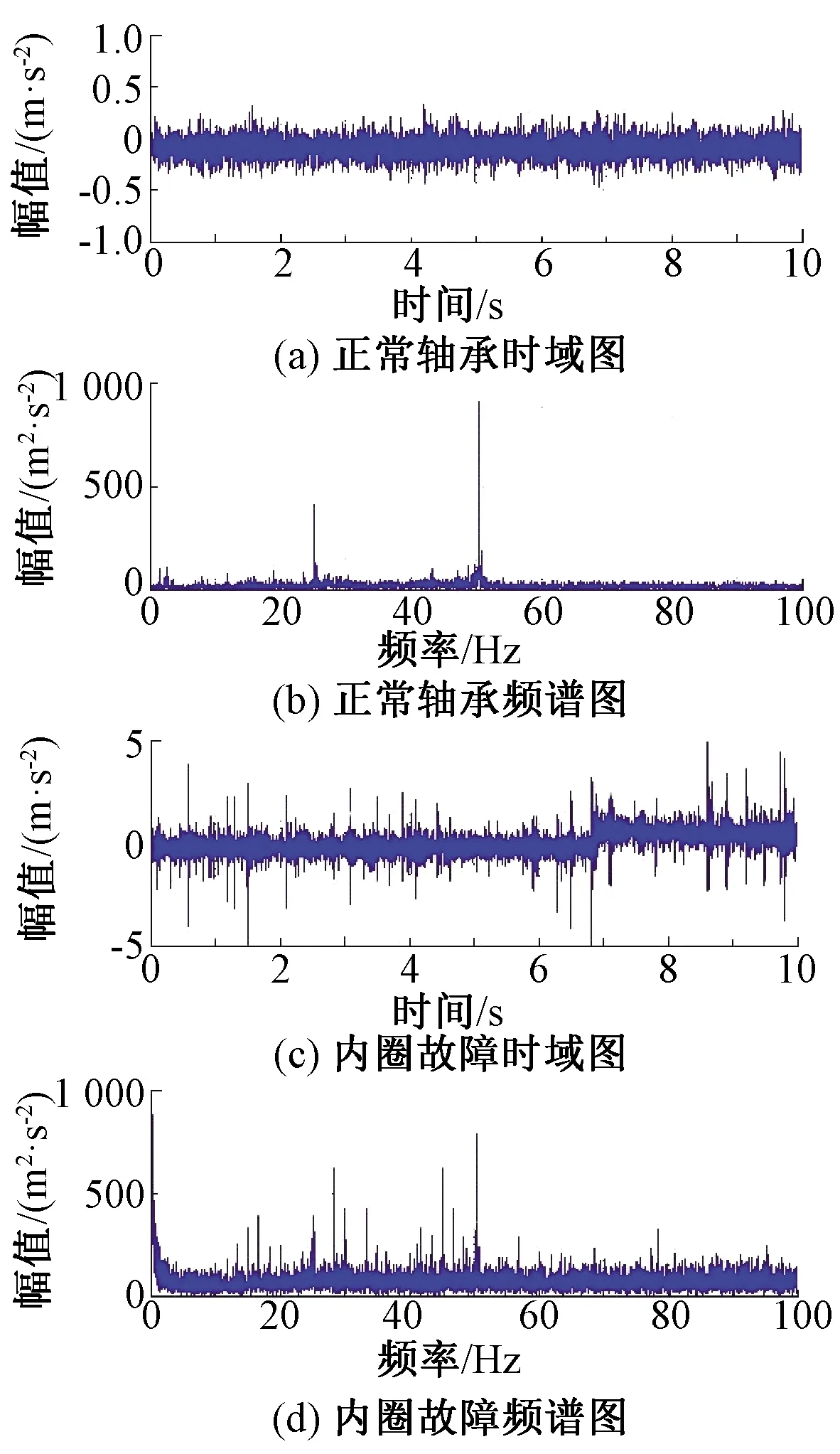
圖5 軸承時域波形圖和頻譜圖

由圖5可知，因為各傳感器檢測信號較為復雜，采集到的信號中常包含背景噪聲和其他不確定性，假如無法完整、準確地提取故障特征，將影響甚至導致故障診斷精度的下降。

針對以上存在的問題，采用本文方法對原始信號建立概率包絡模型，其正常軸承和內圈故障的概率包絡圖如圖6所示。

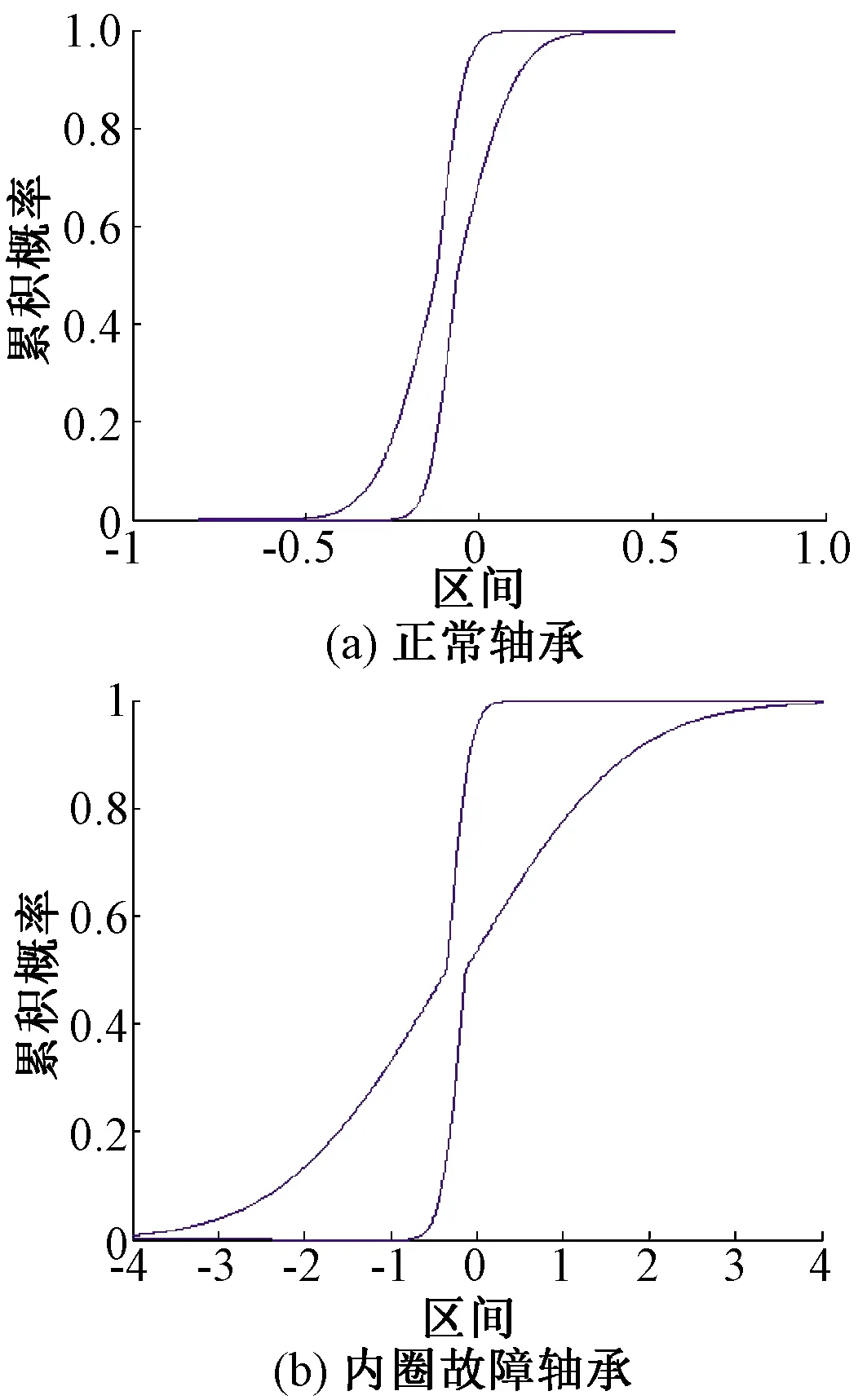
圖6 概率包絡建模

由圖6可知，當軸承出現故障時，所構建的概率包絡模型與正常軸承信號所建光滑曲線包絡相比，既有趨勢的相似，又有形狀特征的區別。如此，將所有信息包裹在概率包絡中，經過概率包絡建模后的原始信號降低了因噪聲干擾和數據不確定性帶來的問題。

經過概率包絡建模后的信號，分別對正常軸承和內圈故障軸承采用概率包絡的特征提取方法得到特征向量，見表1、表2。

本實驗選取累積包絡寬度、矛盾區間統計和累積區間寬度為三類特征向量。當利用SVM故障診斷時，為了避免因參數選取不當造成模型的不準確，采用k折交叉驗證(k-fold Cross Validation)的方法尋求出最恰當的參數值，其中k設為5，最終確認SVM參數C和σ值分別為100和0.01。本實驗分別從正常軸承和內圈故障軸承數據中抽取，每300條數據為一組共200組，每組分別提取概率包絡特征，其中2/3用于訓練SVM生成分類模型，用剩余1/3測試數據進行故障診斷，并給出診斷結果及其分析。

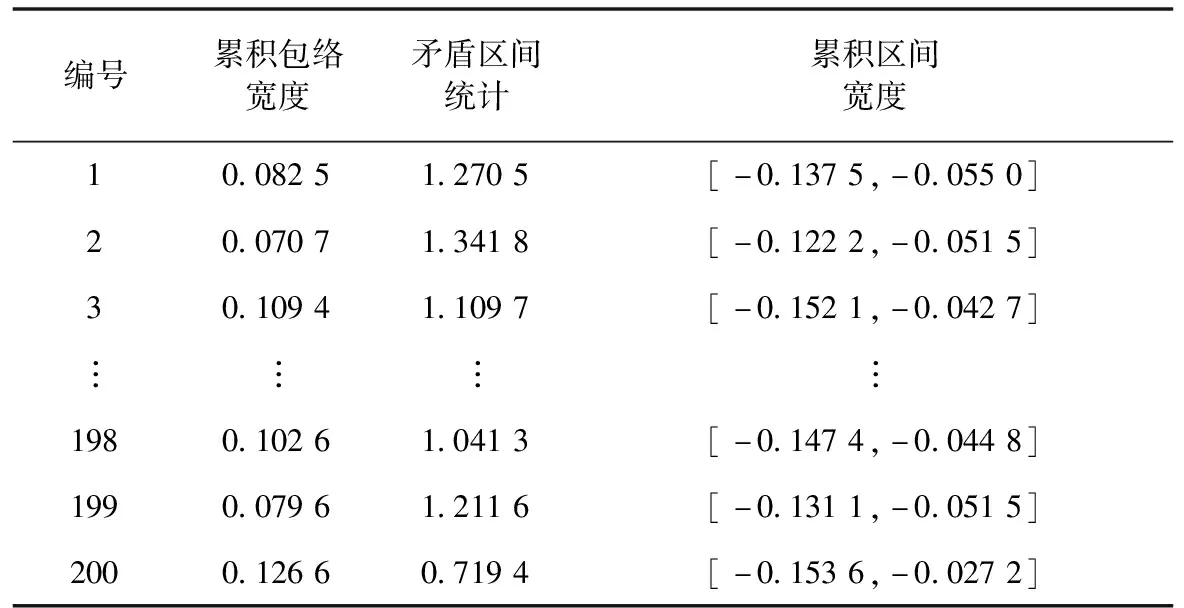
表1 正常軸承特征向量

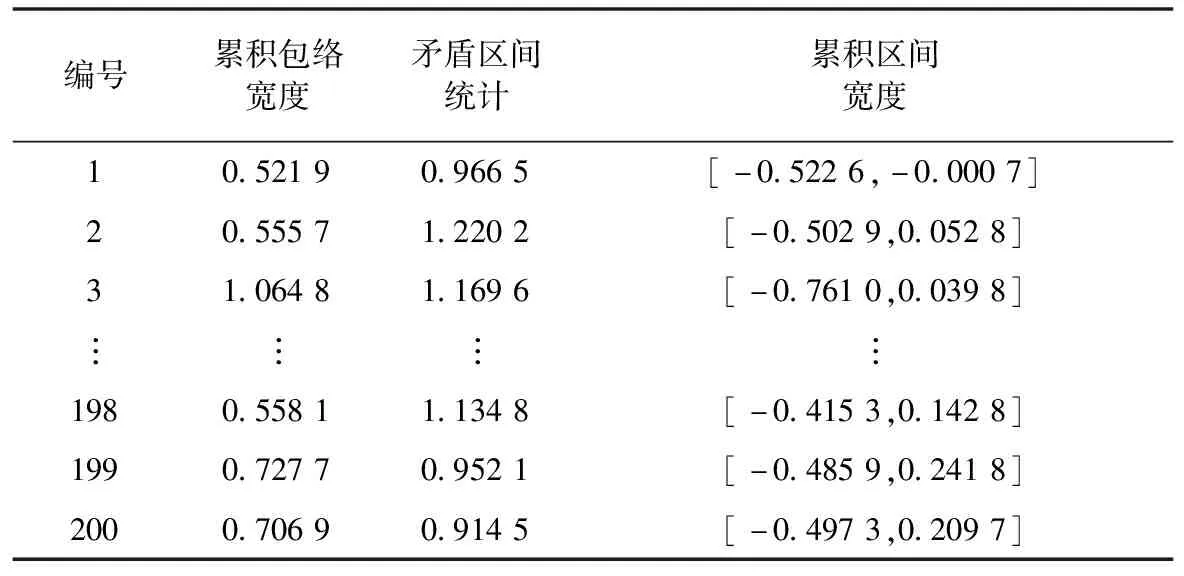
表2 內圈故障特征向量

在相同信號源的條件下，基于相同的SVM分類原理，采用小波變換提取特征，進行訓練和故障診斷(WT-SVM)，與本文方法的診斷結果對比見表3。

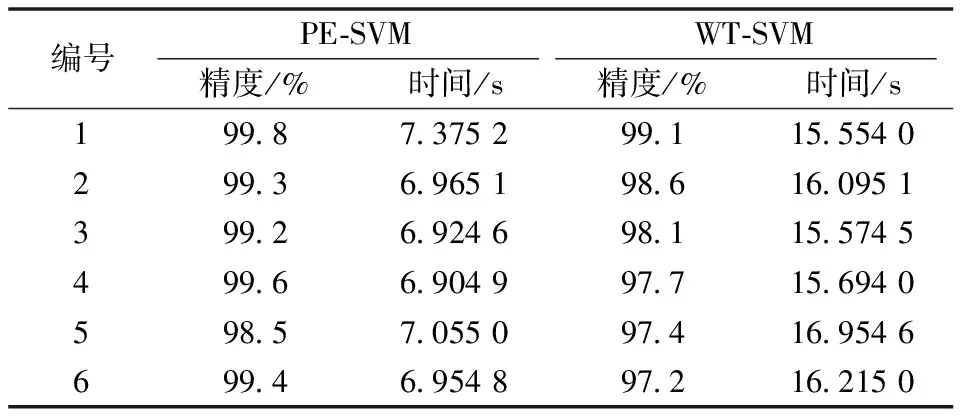
表3 PE-SVM和WT-SVM

從表3可以看出，相對于采用WT-SVM診斷方法而言，采用本文提出的PE-SVM診斷方法不僅在訓練時間上具有明顯的優勢，而且診斷精確度較高。這種差別形成的原因一方面是本文方法使用概率盒來表達參數不確定性，使得對于振動信號不確定性的描述更加全面，提取的特征更具區分度；另一方面，本文提出的基于概率包絡故障診斷算法采用k折交叉驗證來尋找并確定最恰當的超參數，避免了過擬合的問題。

為更好驗證本文方法的有效性，再次進行一組對比實驗。重新從數據集1的軸承3中截取出60 000條數據構成新的原始數據集，部分數據見表4。

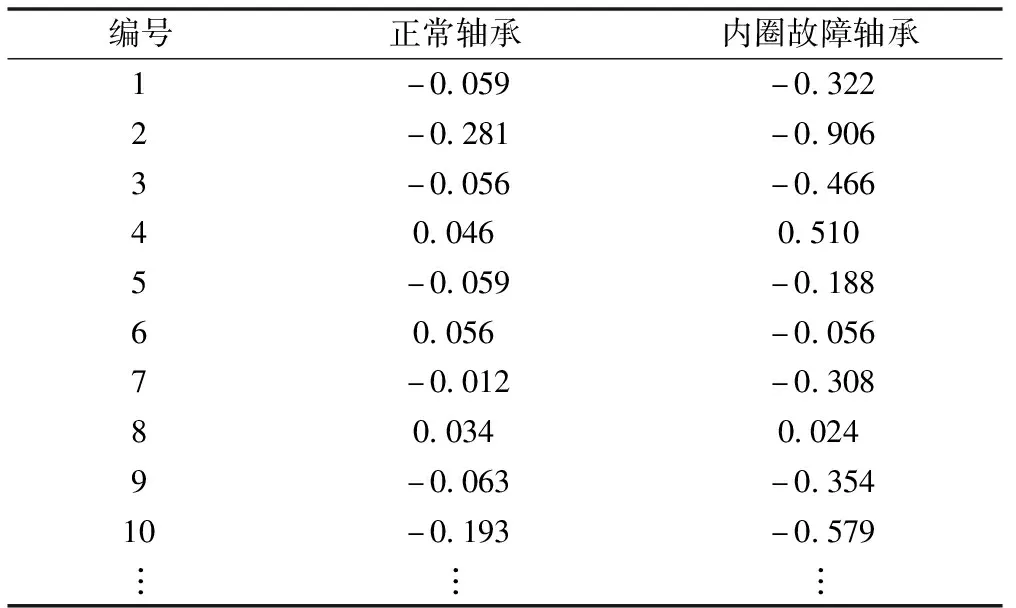
表4 原始數據

采用概率包絡分別對采集到的信號數據進行建模，正常和內圈故障軸承概率包絡模型如圖7所示。

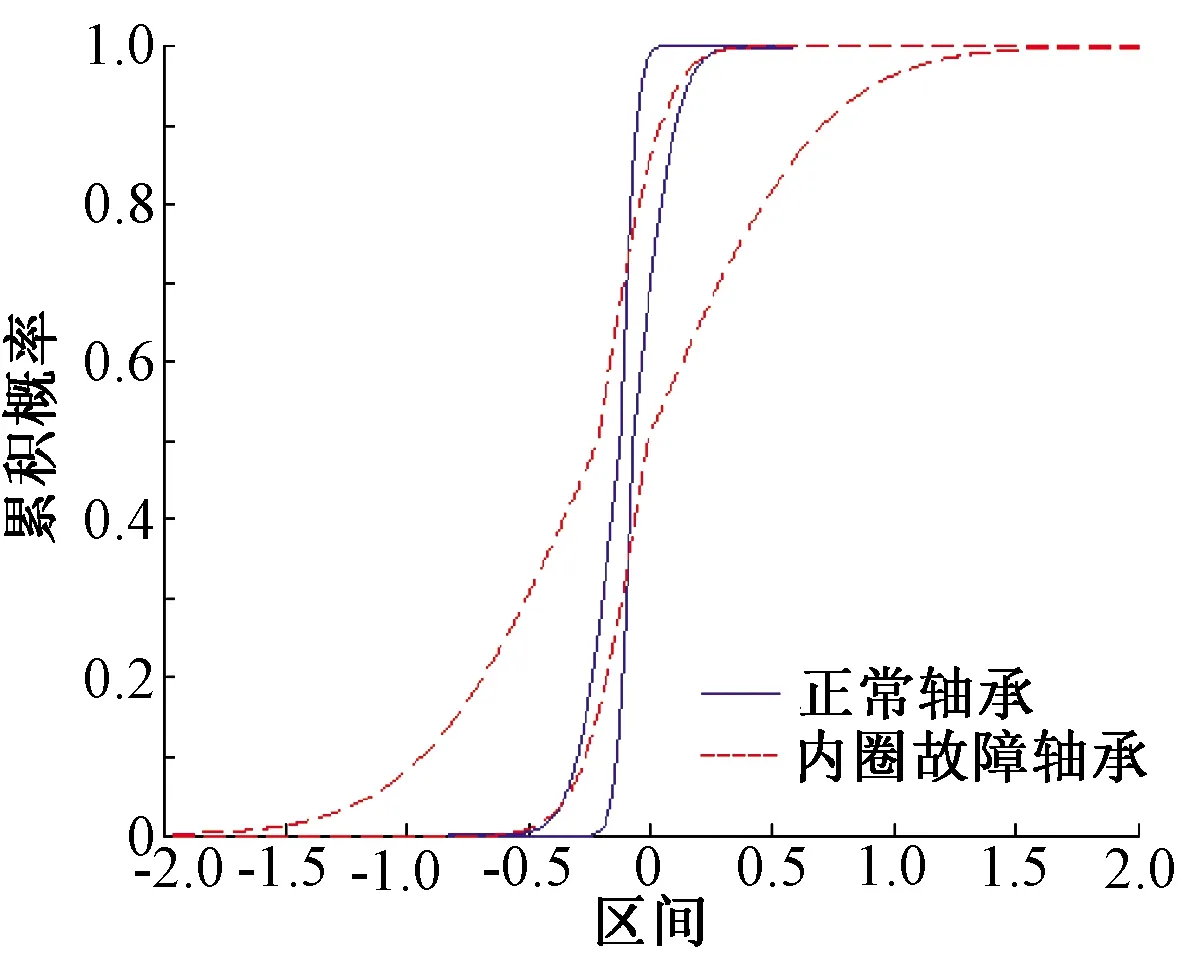
圖7 概率包絡建模

在建模后分別采用PE-SVM診斷方法和基于樸素貝葉斯網絡的概率包絡方法(PE-BN)進行診斷對比分析，即先利用概率包絡對數據進行特征提取，然后分別基于SVM和樸素貝葉斯網絡進行訓練和測試對比。利用概率包絡提取出的正常和內圈故障軸承特征，見表5、表6。

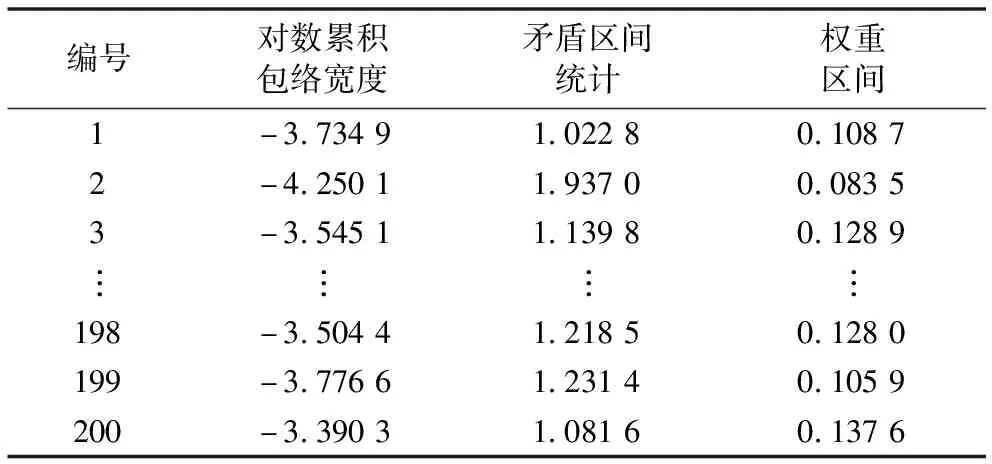
表5 正常軸承特征向量

表6 內圈故障特征向量

此次實驗選取對數累積包絡寬度、矛盾區間統計和權重區間為特征向量作為SVM和樸素貝葉斯網絡的輸入進行故障分類診斷。SVM參數設定采用k折交叉驗證的方法確定出參數值，其中k設為5，最終選取出SVM參數C和的σ值分別為10和0.5，同時將特征值按6∶4隨機分為訓練數據和測試數據，將其分別傳入SVM和樸素貝葉斯網絡中進行故障分類診斷。對比結果見表7。

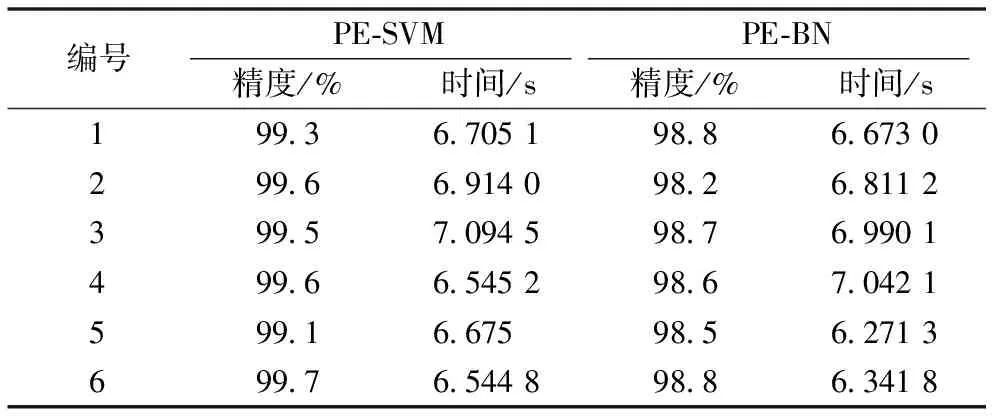
表7 PE-SVM和PE-BN

表7結果是在采用概率包絡提取到相同特征向量的基礎上兩種方法的對比。一方面，表明采用本文提出的PE-SVM方法在訓練時間上與PE-BN方法相當，但是在診斷精確度上優于PE-BN方法。另一方面，兩種方法的診斷精確度綜合平均為99.03%，進一步突顯本文采用概率包絡進行不確性建模和故障特征提取的方法有效性。

為了更好地驗證本文方法的泛化能力，進行了第三次實驗，選取實測輪對軸承數據集中的外圈故障、滾動體故障和正常軸承數據各5 000條，數據采樣頻率為10 240 Hz。對實測信號數據建立概率包絡模型，并提取累積包絡寬度、矛盾區間統計和累積區間寬度為三類概率包絡形狀特征，采用本文PE-SVM方法進行故障診斷，其分類診斷精度和時間見表8。

表8 基于實測數據的診斷結果

由表8可以看出，由于樣本數量的降低和實測平臺部署環境與公開實驗平臺環境差異性，尤其是將外圈、滾動體故障混合在一起診斷，分類診斷精度有所下降，但故障診斷精度仍然穩定在98%以上，并且分類診斷時間大幅縮短，因而表明本文所提PE-SVM故障診斷方法具有良好的泛化能力。

4 結束語

本文針對信號不確定性問題，引入概率包絡理論，將信號的不確定性包裹在概率包絡中，解決了特征提取信息丟失的問題。實驗表明本文方法有效可行，在兼顧診斷模型訓練效率的同時，提高了故障診斷的精確度。本文方法具有較好的泛化能力，除了能用于列車輪對軸承故障診斷之外，對于其他類型的機械故障，也具備良好診斷效果。