考慮接續可靠性的動車組運用計劃優化方法

仝 碩，陳紹寬，劉葛輝，劉 爽，毛保華

(1.北京交通發展研究院,北京 100073; 2.北京交通大學 交通運輸部綜合交通運輸大數據應用技術交通運輸行業重點實驗室,北京 100044)

動車組運用計劃是鐵路客運日常工作的重要組成部分。隨著我國高速鐵路系統的快速發展，動車組開行密度不斷增大，在降低運營成本、提高運營可靠性的要求下，優化動車組運用計劃具有重要的理論意義與實際價值。

既有研究中，動車組運用計劃編制優化問題主要涉及數學問題轉化、運用場景選取、目標函數構造以及求解算法設計4個方面。首先，將動車組運用計劃編制優化問題轉化為多商品流問題和(多)旅行商問題等處理，Abbink等[1]針對單線周期運行圖建立了最小化動車組數量和走行里程的雙目標多商品流優化模型，優化了允許重聯和摘解列車的周轉計劃；Giacco等[2]研究了維修條件下動車組運用計劃，利用TSP問題建立混合整數規劃模型；王超等[3]基于車輛線路問題理論，構建了動車組運行圖與運用計劃一體化優化模型。其次，基于實際情形，既有研究考慮了不同動車組運用方式、空車調撥、非單一編組和非單一車型等不同場景[4-5]，聶磊等[6]用實驗證明空車調撥可以提高動車組利用率，在運行調整時可提高動車組運用的靈活性。然后，優化目標通常考慮動車組數量、動車組運用均衡性、檢修均衡程度、檢修次數等指標，例如，Canca等[7]以車底數最小和均衡性最大為目標；張才春等[8]以動車組數量最少和動車組總檢修時間最小為目標；Cadarso等[9]在目標函數中考慮了運營中的延遲時間和人員需求，以優化路網車底運用計劃的魯棒性，但列車運用過程沒有考慮檢修約束；李建等[10]通過構建0-1整數規劃模型實現了動車組接續時間最小化和動車組檢修前累計運行里程最大化。最后，用于動車組運用計劃模型求解的方法主要包括解析算法和智能算法兩大類，前者主要有商業求解器[3]、分支-切割算法[7]、改進的分支定界法[11]等，后者則以蟻群算法[12]、模擬退火算法[13]、粒子群算法[10,14]等啟發式算法為主。

既有研究較少涉及動車組運用計劃中相鄰列車任務接續的可靠性問題。動車組一般按時刻表執行交路段中的各運行任務，但實際中可能出現由突發事件或隨機擾動造成的晚點情況，如列車到達晚點、檢修(整備)任務完成晚點和空車調撥到達晚點。這類晚點會影響動車組在要求時間內完成接續和周轉，即降低了接續可靠性。作為動車組運用計劃的一部分，動車組接續延誤會產生額外的運營調整和人員費用，所以在編制動車組運用計劃時，應在降低接續時間成本的同時保證較高的接續可靠性。

本文結合我國動車組日常運用中的需求，基于運用網絡圖，應用晚點分布函數和概率論分析動車組接續可靠性，構建考慮動車組檢修和熱備的運用計劃優化模型，設計基于蟻群算法的模型求解算法，并通過案例研究驗證本文提出的方法。

1 動車組運用網絡圖構建

本文通過引入接續可靠性優化動車組的日計劃，這一計劃是動態的，即日計劃均需根據動車組的初始狀態、任務情況進行優化。動車組日計劃需要基于維修歷史數據、綜合接續時間、檢修里程和動車段所能力等約束，安排動車組在新的日計劃中執行的各類任務，包括列車、檢修(整備)和熱備任務。其中，動車組在上一個日計劃中的最后任務是新的日計劃的初始任務，新的日計劃的初始時刻為t0。動車組任務的接續關系見圖1。

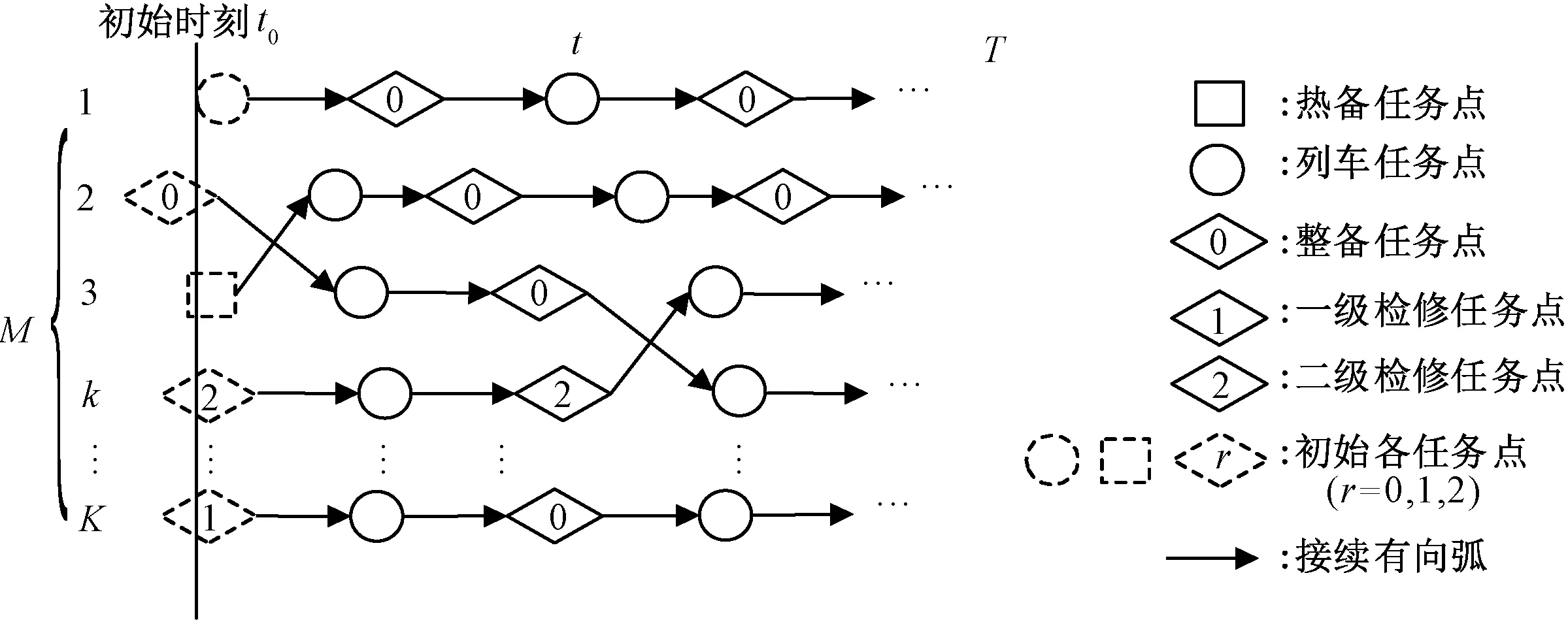
圖1 反映各任務之間接續關系的動車組運用網絡圖

圖1中k為動車組的編號；K為動車組總數；M為動車組集合；t為計劃周期中的時刻，t∈[t0,T]，T為日計劃的結束時刻。

1.1 任務節點

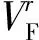
(1)

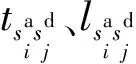
1.2 任務接續有向弧

動車組執行完列車任務后必須執行檢修(整備)任務，一般情況下需要在車站進行整備，之后執行后續列車任務。當累計運行里程達到檢修規定的里程后，需要在運用所進行一級或二級檢修。熱備車在運用動車組故障時執行列車任務，執行熱備任務的動車組需要定期更換且每隔一段時間內需要進行一次一級檢修，以保證熱備車良好的運行狀態。各任務之間的接續弧分為圖2所示的5種類型。

圖2 任務之間的接續關系圖

(1)入檢(整備)接續弧aij∈ANF(i∈VN,j∈VF,φj=0，且滿足式(1))，ANF為入檢(整備)接續弧集合。

(2)出檢(整備)接續弧aij∈AFN(i∈VF,j∈VN,φj=0)，AFN為出檢(整備)接續弧集合。

(3)入備接續弧aij∈AFB(i∈VF,j∈VB,φj=0，且滿足式(1))，AFB為入備接續弧集合。

(4)出備接續弧aij∈ABN(i∈VB,j∈VN,φj=0)，ABN為出備接續弧集合。

2 基于接續可靠性的運用計劃優化模型

2.1 假設和符號定義

為簡化問題的復雜性，提出以下合理假設：

(1)研究的動車組運用計劃基于給定的運行圖，暫未考慮運行圖的調整。

(2)動車組運用模式為不固定區段方式，各站之間允許空車調撥。

(3)動車組日計劃的制定主要考慮運用檢修，運用檢修包括一級檢修和二級檢修。一級檢修周期為3 300 ～4 000 km，二級檢修周期為27 000 ～30 000 km。本文未考慮其他高級檢修，因為高級檢修的停時均大于1 d，超過日計劃的計劃范圍，同時日計劃主要針對當日可用動車組，進行高級檢修的動車組可以在計劃前進行排除。

(4)采用最高允許速度為350 km/h的單一型號且編組固定動車組，暫不考慮動車組重聯、解編的情形。

(5)列車任務完成后需要檢修(整備)時，列車將在當前車站進行檢修(整備)。

為方便模型構建，定義如下符號。

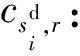
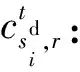
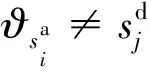
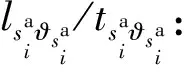
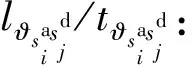
Lr,min(Lr,max):r(r=1,2)級檢修任務的最小(最大)累計運行里程限制。

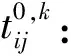
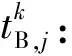
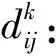
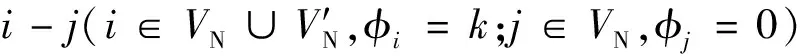
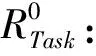
2.2 接續可靠性分析與計算

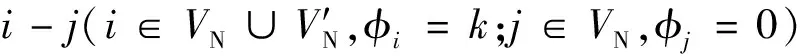
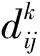
(2)

(3)

根據晚點時間分布和最小接續時間可計算動車組完成列車任務i-j接續的可靠性為

j∈VN,φj=0

(4)

(5)

全部動車組運用日計劃由K列動車組的交路段組成，運用日計劃的接續可靠性定義為全部交路段可靠性的平均值，計算方法為

(6)

考慮工程方案可行性要求，本文設定任一動車組的交路段接續可靠性均需要滿足最低可靠度的要求。

2.3 優化目標與約束條件

基于上述對列車接續可靠性的分析，本文目標函數為動車組運營總懲罰費用最小

(7)

式中：z1為單位計劃接續時間對應的懲罰費用，元/min；z2為空車調撥單位運行里程對應的懲罰費用，元/km；z3為單位接續可靠性下降對應的懲罰費用，元。z1和z2通過調研獲得。

式(7)第一項表示動車組的計劃接續時間總懲罰費用，除了必要的運行時間，計劃中的接續時間主要表示動車組的在站等待時間，接續時間越小表示動車組的運用效率越高；第二項表示由空車調撥產生的懲罰費用；第三項表示由接續風險產生的懲罰費用，通過接續可靠性表示接續風險。由于接續可靠性覆蓋了全部接續的列車任務，本文假設接續可靠性指標與前兩項費用具有同等重要度，因此費用結果具有相同的數量級。

約束條件為

(8)

(9)

(10)

(11)

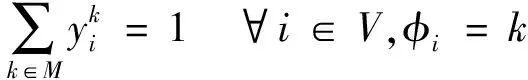
(12)

(13)

(14)

(15)

(16)

(17)

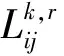
2.4 模型求解算法

本文針對所建立的優化模型設計蟻群算法：一只螞蟻的路徑表示一列動車組的運用日計劃，所有螞蟻的路徑可表示全部動車組的運用日計劃。算法設置最大迭代次數，每一次迭代中，設置時間步長t∈[t0,T]推動計算。根據各弧的轉移概率實現列車任務的分配，并根據信息素濃度的變化不斷更新轉移概率，在系統時間結束時完成一次迭代，需要保證安排全部的列車任務。計算當前代的目標函數值并更新最優方案，之后更新全局信息素并繼續迭代，在迭代達到最大次數時終止算法。其中，轉移概率公式和全局信息素更新規則采用文獻[15]的方法。

上述過程中可以通過接續控制保證約束式(8)～式(16)，為了保證解的可行性，將約束式(17)構造為懲罰函數并加入目標函數

(18)

式中：z4為懲罰系數，由于全部動車組的日計劃接續可靠度小于目標要求是不可接受的情形，因此設定懲罰系數z4的數量級為連續接續任務可靠度懲罰系數z3的3倍，以剔除不滿足約束式(17)的解。

解空間的構造方法和啟發式信息素的設置如下：

(1)構造解空間

Step1初始化變量和參數，按照2.1節生成非列車任務的相關參數和接續條件，設置初始時間為t0、時間步長為1 min。

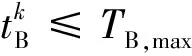
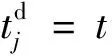
Step5令t=t+1，如果t≤T，進行Step2，直到t>T，結束算法。

(2)啟發式信息素更新

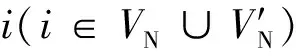
(19)

式中：b為啟發式因子重要程度參數。

3 案例研究

本文以某客運專線A、B、C 3站間的動車組運用日計劃編制進行案例研究。3站都有配屬的動車運用所，且3站間開行AB、AC兩條線路的列車，通過調研已知28對列車(編號為1～56)的時刻表、各動車組初始任務(初始列車任務編號首位為0)和3站配屬動車組情況、檢修能力、晚點分布等基本數據。假設熱備任務和檢修任務之間的距離(時間)忽略不計，與本文研究直接相關的其他主要參數設置見表1。

表1 案例研究相關參數取值

文本采用MATLAB 2014a實現所設計的蟻群算法，算法中信息素重要程度參數α=1，啟發式因子重要程度參數b=10，信息素增加強度系數Q=10 000，信息素蒸發系數v=0.3，迭代代數為150代，多次求解運算后獲得結果見表2。

表2中，方案1是未考慮列車接續可靠性的運用方案，方案2是考慮列車接續可靠性的優化運用方案。方案1中交路段可靠性低于50%的交路段有3個，分別是1、3和8號動車組交路段，特別地有交路段1的可靠性非常低，執行這些交路段的動車組在任務到達(完成)晚點時不能正常接續下一列車任務的概率很大；而方案2中不存在接續可靠性低于50%的交路段，一方面全部交路的整體可靠性有所提高，另一方面低可靠性的交路段數量減少，整體上較大幅度地降低了動車組接續的風險。

兩個方案的進一步指標分析結果見表3。由表3可知，方案2中已經不存在0～49%的交路段，比方案1減少了3個，而可靠性大于90%的交路段個數增加了7個；兩個方案使用的動車組總數沒有變化，表明適當提高接續可靠性的優化方案不會額外增加動車組數量。方案2的動車組接續時間懲罰費用比方案1多199 600元，即增加1 996 min的接續時間，主要原因是方案2中部分熱備車承擔運行任務，而接續時間是以列車任務為基準進行計算的，因此相比方案1會增加較多的接續時間。例如，動車組10、23的初始接續時間之和為1 992 min，說明方案2不會對既有運營條件有較大的影響。方案2的空車里程有所增加，實際上為1個AC方向的空車運行變為1個AB方向的空車調撥。接續可靠度方面，方案2將平均接續可靠性提高了16.74%，從而有效優化了接續風險總懲罰費用和總費用。以上分析表明運營條件基本不改變的情況下提高動車組接續可靠性可以有效避免因為晚點等運行波動造成的運營風險。

表2 考慮列車接續可靠性的運用日計劃方案

表3 動車組運用計劃優化前后指標對比

4 小結

本文定量分析了動車組運用計劃的列車接續可靠性，以總懲罰費用最小建立了運用計劃優化模型，設計基于蟻群算法的求解方法，通過算例驗證了模型算法。結果表明：考慮列車接續可靠性的動車組運用計劃可以減少接續可靠性低的任務接續的數量，雖然會增加空車運行里程和接續時間，但可以有效降低接續風險總懲罰費用。

提高動車運用計劃中的列車接續可靠性，減少因動車運用計劃未實現而重新調整接續的列車數量，可為優化動車組運用計劃提供依據，也能更好地適應運營環境的變化。今后將進一步研究未實現可靠接續的動車組運用計劃的優化調整方案。