上游泵送機械密封潤滑膜固體顆粒沉積特性研究

陳匯龍，桂鎧，韓婷，謝曉鳳，陸俊成，趙斌娟

（江蘇大學能源與動力工程學院，江蘇鎮江212013）

引 言

上游泵送機械密封主要是利用密封端面泵送槽的泵送效應和流體動壓效應，實現密封動靜環之間的非接觸，理論上可實現被密封介質的零泄漏甚至零逸出[1-3]。同時，由于上游泵送機械密封端面間形成的微米級潤滑膜能有效改善端面潤滑條件，達到了降低摩擦和減少磨損的目的，因此已被廣泛應用于石油化工等相關領域[4-5]。

在上游泵送機械密封實際運行過程中，除了密封介質會將微小固體顆粒帶入密封間隙外，端面泵送槽的泵吸作用也極易將下游空氣或沖洗冷卻液夾雜的微小固體顆粒吸入到密封端面潤滑膜中。這些固體顆粒的進入，一方面使潤滑膜流場特性發生變化，另一方面會出現沉積現象，嚴重時將會導致泵送槽的堵塞甚至喪失泵送能力，造成機械密封端面摩擦功耗的增加和密封端面的加劇磨損[6-7]。據統計，發生故障的機械密封中近一半是由于顆粒磨損造成的[8]。固體顆粒在間隙潤滑膜中的運動、沉積規律與潤滑膜多相流動特性密切相關，此外由于密封端面微造型或帶有波紋等，當潤滑膜局部壓力低于飽和蒸氣壓時將出現空化現象，進一步增加了潤滑膜中固體顆粒運動沉積的復雜性[9-10]。因此，深入研究掌握潤滑膜中固體顆粒沉積特性是設計性能優秀、運行穩定的上游泵送機械密封必須面對的重要問題之一。

對于密封腔含固體顆粒流場的研究，Merati等[11]在考慮葉片上平衡孔的影響下，針對錐形密封腔內固體顆粒的運動進行了試驗研究，得到了不同條件下的顆粒軌跡及分布情況，發現粒徑大約為40 μm 的固體顆粒會隨流做螺旋運動，而大直徑顆粒則聚集于底面并沿螺旋軌跡移動，造成了密封腔表面的磨損。Azibert 等[12-13]采用離散相模型對不同工況下的離心泵機械密封密封腔流場進行了數值模擬，并針對固體顆粒聚集于密封端面附近這一現象設計了一種帶有固體分離裝置的離心泵機械密封，計算得到了不同流體黏性、不同沖洗條件下的固體顆粒分布情況。趙龍[14]針對帶有固體顆粒的不同尺寸機械密封密封腔進行了固液兩相流數值模擬，發現在錐形密封腔以及帶沖洗液情況下排出固體顆粒效果更好。對于密封間隙含固體顆粒流場的情況，嚴彥等[15]對一種動環開設引流孔的雙向自泵送流體動靜壓型機械密封泵入和泵出時的工作性能進行了研究，發現這種自泵送流體動靜壓型機械密封在兩種工作方式下都具有良好的抗顆粒干擾性。Chen 等[16]在此基礎之上，基于Fluent 軟件計算分析，得到了其在不同顆粒直徑、轉速、壓差、液膜厚度和顆粒體積濃度下的自清潔特性。彭旭東等[17]以核主泵所用U 型槽動壓密封環為對象，對介質中的雜質顆粒對密封端面的磨損問題展開了研究，結果表明端面動壓槽根部產生的初期磨損會導致潤滑膜剛度和泄漏率增大。陳匯龍等[18]采用Mixture 模型對上游泵送機械密封潤滑膜固液兩相流動特性進行了研究，得到了密封端面潤滑膜內部微小固體顆粒的分布規律及其對密封性能的影響。Chen 等[19-20]基于歐拉多相流模型建立了密封微間隙氣液固多相流動計算模型，得到了間隙密封氣液固多相潤滑膜的內流場特性并研究了固體顆粒的直徑、顆粒進口體積分數、氣核含量等氣-固相物理參數對潤滑膜空化及潤滑性能的影響關系。從現有國內外研究來看，關于機械密封端面微間隙潤滑膜中固體顆粒的運動特性及分布規律的研究已取得一定的進展，但仍不夠系統深入，尤其是對固體顆粒沉積特性的研究還很缺乏，加強這方面的研究具有重要的理論和現實意義。

本文利用Fluent 中的DPM 模型，考慮雙向耦合作用，結合空化模型進行數值模擬，以清水為密封介質，研究固體顆粒直徑、顆粒進口體積分數、轉速、介質壓力、潤滑膜厚度等對上游泵送機械密封端面潤滑膜固體顆粒沉積特性的影響規律，為提高上游泵送機械密封性能及適應能力提供參考依據。

1 物理模型

1.1 幾何模型

圖1 為典型的上游泵送機械密封端面造型[21]。螺旋槽開在動環端面，型線為對數螺旋線，在極坐標下描述為

式中，ri為螺旋槽內半徑，mm；φ 為螺旋線展開角，(°)；α為螺旋角，(°)。

圖1 機械密封端面螺旋槽造型Fig.1 Face structure of spiral groove mechanical seal

利用三維造型軟件建立參數化螺旋槽上游泵送機械密封微間隙潤滑膜幾何模型，其參數為: 螺旋槽內半徑ri= 26 mm；密封面外半徑ro=31 mm；槽根圓半徑rg=28.5 mm；螺旋角α=21°；槽寬比γ=0.5；槽徑比β=0.5；槽深hc=8 μm；密封間隙潤滑膜厚度h=3 μm；槽數Ng=12。密封間隙潤滑膜三維模型如圖2 所示，為便于觀察，在膜厚方向放大1000 倍表示。

1.2 網格劃分及邊界條件

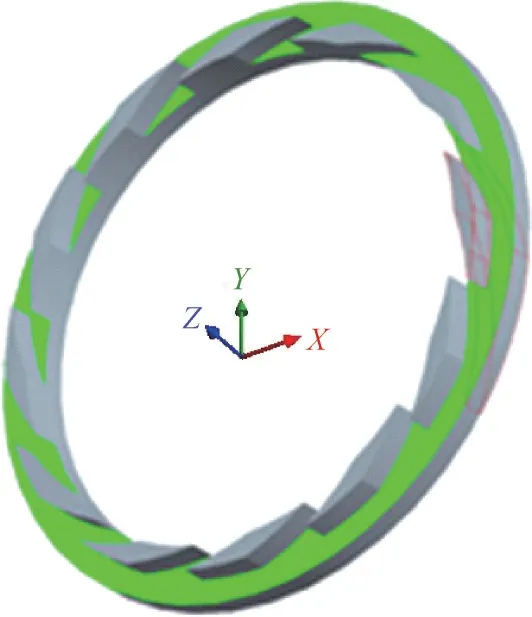
圖2 端面潤滑膜三維模型Fig.2 Three-dimensional model of lubricating film

由于螺旋槽呈周期性排列，故只選取潤滑膜的1/Ng作為計算域，在前處理軟件Gambit 中采用非結構網格進行網格劃分。為了提高計算效率和準確性，網格劃分過程中進行了網格無關性檢驗，針對33萬～172萬不同網格數的網格進行模擬計算，衡量參數為開啟力與固體顆粒沉積率，運行轉速為3000 r/min，介質壓力為0.2 MPa。不同網格方案的潤滑膜固體顆粒沉積率、開啟力計算結果如圖3 所示。由圖3 可知，隨著網格數增大，計算偏差逐漸減小，網格數量超過59萬以后計算結果基本不變，此時認為網格數對計算結果的影響很小，綜合考慮收斂速度與精確度，采用59 萬網格方案，最終網格劃分結果如圖4所示。

圖3 網格無關性檢驗Fig.3 Grid independence verification

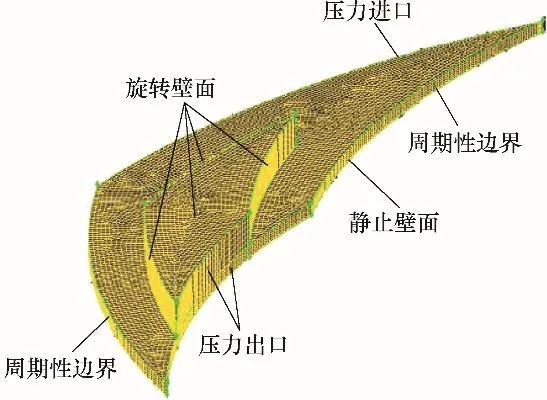
圖4 1/Ng潤滑膜網格及邊界條件Fig.4 1/Ng lubrication film mesh and boundary conditions

在Gambit 中設置如圖4 所示的邊界條件，螺旋槽內潤滑膜設置為旋轉水體；微間隙內潤滑膜設置為靜止水體；動環表面、螺旋槽的軸向三個側面及槽底面均設置為旋轉運動壁面，靜環表面設置為靜止壁面。進口壓力為密封介質壓力，取值范圍為0.2～1.6 MPa，出口壓力為大氣壓力0.101325 MPa，轉速取值范圍為1000～6000 r/min。

2 數學模型

2.1 基本假設

本文以清水為密封介質，即間隙內流場連續相為清水，離散相固體顆粒的密度為3450 kg/m3，黏度折合連續介質的黏度為0.04 Pa·s[22]，顆粒直徑范圍為0.25～3.0 μm，顆粒體積分數在10%以下。為了降低上游泵送機械密封潤滑膜流場計算的復雜性，忽略對計算結果影響較小的因素，本文根據研究對象的特點作如下假設[23-25]：

（1）間隙液體流動為層流且為不可壓縮流體；

（2）忽略潤滑膜受溫度的影響，且介質溫度、黏度保持不變；

（3）潤滑膜與密封端面無相對滑移；

（4）忽略密封環粗糙度的影響；

（5）固體顆粒均為球形且大小均勻，不考慮相變；

（6）潤滑膜與固體顆粒保持恒溫25℃，即不考慮顆粒的熱泳力、布朗力及熱輻射；

（7）忽略Magnus 升力、Saffman 力、Basset 力、附加質量力與科氏力。

2.2 連續相基本方程

混合物模型的連續性方程為[26-28]

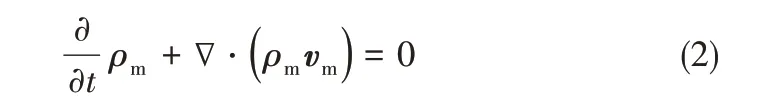
混合物的動量方程可以通過對所有相各自的動量方程來獲得，可表示為

由第二相( p) 的連續性方程，可得第二相的體積分數方程為

式中，ρm為混合密度，kg/m3；vm為質量平均速度，m/s；μm為混合黏性系數，Pa·s；F為體積力，N；n為相數；αk為第k 相的體積分數；ρk為第k 相的密度，kg/m3；vdr,k為第k相的漂移速度，m/s。

2.3 離散相基本方程

根據上述基本假設，固體顆粒在密封潤滑膜氣液固流場中主要受到壓強梯度力FP、繞流阻力FD、重力Fg及由于旋轉施加在顆粒上的離心力F離等作用力，因此離散相固體顆粒在Lagrangian 坐標系下的受力平衡方程為[29]

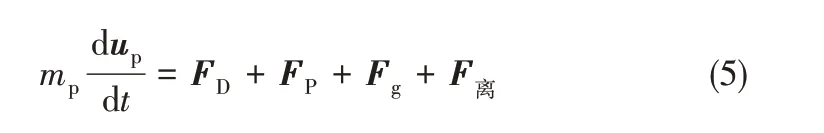
其中，

式中，Cd為曳力系數；mp為顆粒質量，kg；up為顆粒速度，m/s；ρ 為流體密度，kg/m3；u 為流體速度，m/s；ρp為顆粒密度，kg/m3；dp為顆粒直徑，m；?p 為壓力梯度，Pa/m；ωp為旋轉軸角速度，rad/s。

2.4 DPM模型選擇與計算流程

密封間隙固體顆粒來源通常有三個方面，即密封介質含有固體顆粒、密封端面磨損產生固體顆粒、螺旋槽內徑負壓吸入環境固體顆粒等，考慮到問題的復雜性，本文暫選擇固體顆粒從螺旋槽內徑側吸入的問題進行模擬研究。由于本文研究的上游泵送機械密封潤滑膜中離散相的體積比很小且顆粒群的控制體積大小并非遠小于流場尺寸，因此本文選取DPM模型進行模擬計算[30]。

本文先計算連續相穩態流場直至收斂，再加入離散相顆粒計算求解，連續相每計算10步后進行顆粒軌跡追蹤直至收斂，同時考慮離散相與連續相的雙向耦合作用。模擬過程中假設顆粒直接在入口存在且均勻分布，即顆粒入射初速度為0。將螺旋槽內徑側與外徑側定義為Escape 邊界，其他所有面定義為Reflect 邊界且均為完全彈性碰撞，反彈系數為1，計算流程如圖5所示。

2.5 空化模型選擇

目前Fluent 中有兩種空化模型,即Zwart-Gerber-Belamri 空 化 模 型[31]和Singhal 等[32]的 空 化 模型。Singhal 等的空化模型主要考慮了不可冷凝氣體對空化的影響，適合應用于存在液相相變、湍流壓力脈動等場合。而Zwart-Gerber-Belamri 空化模型假設空化產生的氣泡尺寸相同，局部均衡性更好，同時也相對比較成熟。因為本文的密封介質為清水，密封端面微間隙流動為層流，也并未考慮液相相變的情形，同時從文獻[33-35]可知，采用Zwart-Gerber-Belamri 空化模型的計算模擬結果比Singhal 等的空化模型更接近試驗值，穩定性也較好，因此本文選用Zwart-Gerber-Belamri 空化模型。空化邊界條件為：當潤滑膜內局部壓力小于飽和蒸汽壓力時，空化發生，空泡內壓力為飽和蒸汽壓力且泡壁壓力梯度為0，飽和蒸汽壓力為3540 Pa。

圖5 計算流程圖Fig.5 Flow chart of calculation

2.6 求解設置

采用三維雙精度求解器，求解器基于壓力速度耦合SIMPLEC 算法求解，擴散相梯度差值采用Least Squares Cell Based 格式，動量采用一階迎風差分格式，體積分數采用一階迎風差分格式，收斂精度為10-5。

3 計算結果及分析

一定量的顆粒由潤滑膜內徑側進入后，一部分將在運動中通過潤滑膜內徑側或外徑側離開潤滑膜分別返回下游或進入密封腔，剩余的部分則沉積在密封潤滑膜中，為此，將殘留在潤滑膜中的顆粒數與從潤滑膜內徑側進入的總顆粒數之比定義為固體顆粒在機械密封潤滑膜中的沉積率。

3.1 模型有效性驗證

為了檢驗本文模型設置的正確性，采用本文模擬方法計算文獻[36]中螺旋槽氣體動壓軸承槽數為12 時亞微米級顆粒物沉積數量隨顆粒直徑的變化規律，計算結果如圖6 所示。由圖6 可知，本文模擬方法得到的結果與文獻吻合較好。

圖6 固體顆粒沉積數量模擬結果對比Fig.6 Comparison of simulation results of solid particle deposition

3.2 連續相流場

圖7 為轉速3000 r/min、介質壓力0.2 MPa、顆粒直徑3 μm、顆粒進口體積分數10%、潤滑膜厚度3 μm 時，連續相流場穩定后的潤滑膜壓力分布以及氣泡相體積分數分布情況。由圖7（a）可見，在螺旋槽外槽根處存在高于介質壓力的最大靜壓，并以此為中心形成壓力梯度，在壩區起到局部阻止高壓側液體向低壓側流動的作用，而在螺旋槽迎風側堰區存在局部可能促進泄漏的作用；同時在螺旋槽內槽根至背風側堰區存在低壓區，能夠將高壓側流向低壓側的泄漏液體吸收并向高壓側泵送，起到減少或杜絕泄漏的作用。局部空化出現在螺旋槽背風側中部堰區，如圖7（b）所示。

3.3 顆粒直徑對沉積分布及沉積率的影響

圖8 為不同顆粒直徑下固體顆粒沉積分布云圖。由圖8 可知，沉積顆粒主要位于槽內低壓區上游，空化區上游邊界圓周和外槽根及其圓周上也出現沉積。說明固體顆粒進入槽區后，位于低壓區且速度較低的顆粒，沒能到達螺旋槽迎風側獲得剪切能量而導致沉積，進入空化區上游邊界的顆粒受潤滑膜周向流動的帶動而沿周向分布，而進入剪切區的顆粒獲得能量后一部分被外槽根攔截沉積并受外槽根周向壓力梯度及連續相周向流動的帶動而沿周向分布，另一部分到達壩區在離心力和壓力梯度力作用下從外徑側逃逸。粒徑較小時，較多沉積于低壓區，粒徑較大時空化外邊界和外槽根圓沉積數量增大。

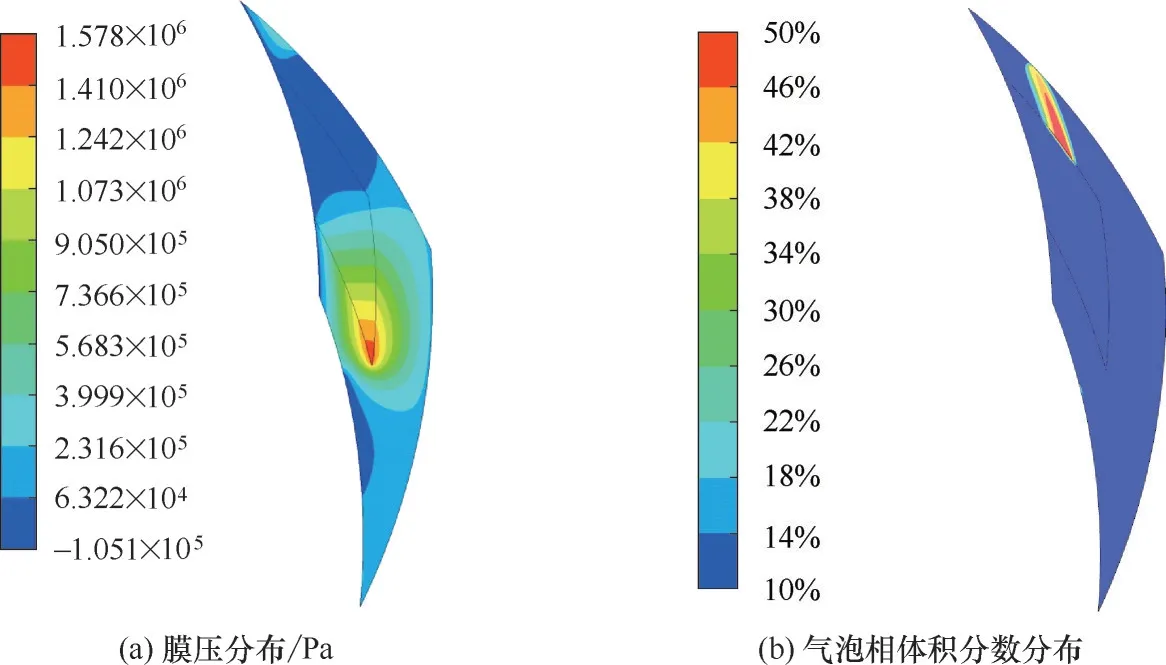
圖7 連續相流場計算結果Fig.7 Calculation results of continuous phase flow field

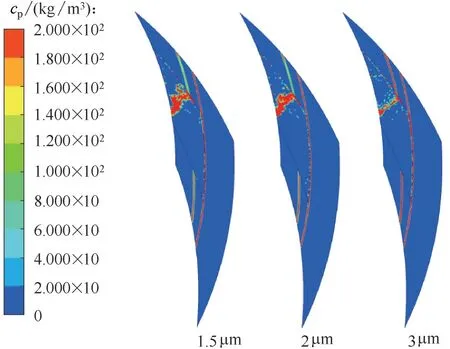
圖8 不同顆粒直徑下固體顆粒沉積分布Fig.8 Deposition distribution of solid particles under different particle diameters

圖9 為顆粒進口體積分數10%、介質壓力0.2 MPa、轉速3000 r/min、潤滑膜厚度3 μm 時沉積率隨顆粒直徑的變化規律。

由圖7、圖9 可以看出，當顆粒直徑為1～1.5 μm時，沉積率隨顆粒直徑的增大而較快增大，說明顆粒直徑增大受到的離心力也增大，跟隨性減弱，隨密封泄漏液從內徑側逃逸的顆粒減少，同時，從螺旋槽剪切中獲得能量而到達壩區的顆粒，雖然也因離心力增大而更易從外徑側逃逸，但其數量相對較小；當顆粒直徑為1.5～2 μm 時，離心力仍增大，但指向內徑的壓強梯度力也增大，因此，從內徑側逃逸顆粒的減少趨緩，而外徑側逃逸顆粒因離心力和指向外徑的壓強梯度力的增大而增多，使沉積率略微下降；當顆粒直徑繼續增大至3 μm 時，內徑側逃逸繼續減少，但因顆粒直徑已逼近密封間隙尺寸，加上顆粒重力（指向動環面）增大，顆粒受外槽根攔截的概率增大，外徑側逃逸增多的速率下降，導致沉積率上升。繞流阻力因微顆粒總體跟隨性較好，故影響相對較小。

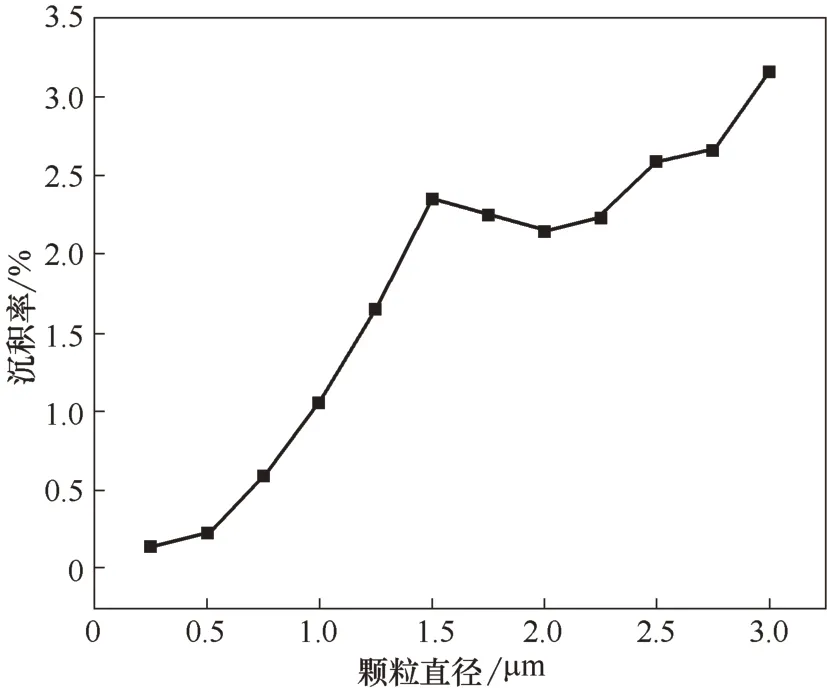
圖9 顆粒直徑對沉積率的影響Fig.9 Influence of particle diameter on deposition rate

3.4 轉速對沉積分布及沉積率的影響

圖10 為固體顆粒直徑為3 μm 時，不同轉速下固體顆粒沉積分布云圖。當轉速為1000 r/min 時，顆粒主要聚集于槽區背風側附近低壓區，同時在密封外徑側出現沉積并沿周向分布，這是由于轉速較低，最高膜壓也較低，壩區徑向壓力梯度力較小，部分顆粒在內徑側隨正泄漏（壓力出口方向的泄漏）逃逸，而部分顆粒因未能從外徑側逃逸而沉積。當轉速達到5000、6000 r/min 時，顆粒主要沉積于槽內低壓區背風側及外槽根內側。說明較大的離心力和壓力梯度力使到達壩區和堰區的顆粒基本隨負泄漏從外徑側逃逸。

圖10 不同轉速下固體顆粒沉積分布Fig.10 Deposition distribution of solid particles under different speed

圖11 為顆粒進口體積分數10%、進口壓力0.2 MPa、潤滑膜厚度3 μm 時顆粒不同直徑下沉積率隨轉速的變化規律。圖11 表明，隨著轉速的增大，沉積率雖有小波動但總體呈下降趨勢。這說明轉速較低時顆粒隨正泄漏逃逸的數量低于高轉速時隨負泄漏逃逸的數量，轉速增大導致顆粒受到的離心力和壓力梯度力均增大，成為影響顆粒運動的主要因素，顆粒直徑越大受影響越明顯，轉速越高從外徑側逃逸的顆粒越多。

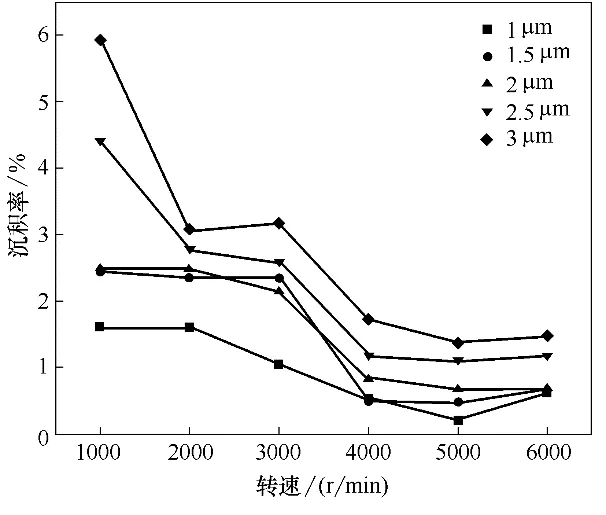
圖11 轉速對沉積率的影響Fig.11 Influence of speed on deposition rate

3.5 介質壓力對沉積分布及沉積率的影響

圖12 為固體顆粒直徑為3 μm 時，不同介質壓力下固體顆粒沉積分布云圖。由圖12可見，介質壓力的升高，總體上使外槽根處的固體顆粒向內徑側推移，特別是介質壓力達到1.6 MPa 時，外槽根處及堰區空化部位基本沒有沉積顆粒，說明介質壓力升高阻礙了顆粒向外槽根運動，同時使堰區空化區域縮小甚至消失。

圖12 不同介質壓力下固體顆粒沉積分布Fig.12 Deposition distribution of solid particles under different medium pressure

圖13 為顆粒進口體積分數10%、轉速3000 r/min、潤滑膜厚度3 μm 時不同顆粒直徑下沉積率隨介質壓力的變化規律。由圖13可知，在所研究的介質壓力范圍內不同直徑顆粒的沉積率均隨介質壓力的增大而降低，且顆粒直徑越大沉積率下降的幅度越大，說明介質壓力的升高，增大了促使內徑側泄漏的潤滑膜壓強梯度力，導致從內徑側離開潤滑膜的顆粒增多，沉積率下降，而顆粒直徑越大所受的壓強梯度力越明顯，沉積率的下降也越明顯。

圖13 介質壓力對沉積率的影響Fig.13 Influence of medium pressure on deposition rate

3.6 顆粒進口體積分數對沉積分布及沉積率的影響

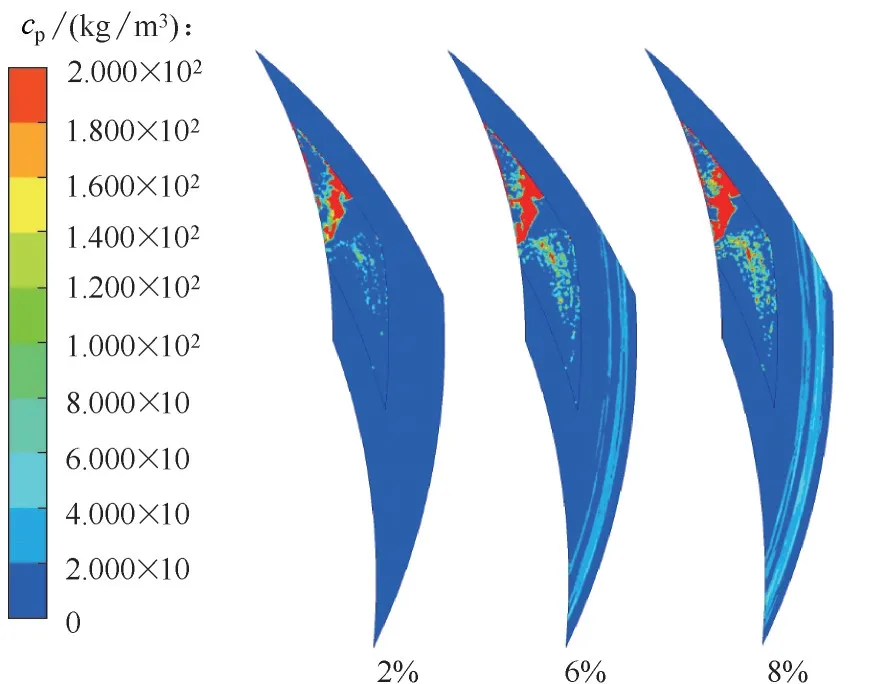
圖14 不同顆粒進口體積分數下固體顆粒沉積分布Fig.14 Deposition distribution of solid particles under different particle import volume fraction

圖14 為固體顆粒直徑為3 μm、轉速為1000 r/min 時，不同顆粒進口體積分數下固體顆粒沉積分布云圖。由圖可知，固體顆粒主要聚集于螺旋槽低壓區上游，但隨著顆粒進口體積分數的提升，在螺旋槽低壓區上游沉積量增大的同時，沉積部位向外槽根和壩區拓展，壩區的沉積顆粒沿周向分布。說明顆粒進口體積分數的提升，受到螺旋槽剪切而獲得能量的顆粒明顯增多，到達槽內高壓區和壩區的顆粒增多，導致相應區域沉積量增加。

圖15 為介質壓力0.2 MPa、轉速3000 r/min、潤滑膜厚度3 μm 時不同轉速下顆粒沉積率隨顆粒進口體積分數的變化規律。由圖15可知，隨著顆粒進口體積分數的增大，沉積率總體呈現略微下降的趨勢，在轉速升高時出現微小波動但規律性不明顯。這說明在相同的工況和顆粒直徑下，由于研究中的顆粒進口體積分數較低，體積分數的變化對流場影響小，固體顆粒的受力及運動的變化也比較小，顆粒進口體積分數的改變主要是改變了沉積的絕對數量而已，對沉積率影響較小。至于隨顆粒進口體積分數增大沉積率略有下降的現象，可能是由于顆粒進口體積分數的增大使多相流黏度和密度有所提升，動壓效應有所增強，壓強梯度力造成的從潤滑膜內徑側逃離的顆粒增多的緣故。

3.7 潤滑膜厚度對沉積分布及沉積率的影響

圖16 為上述條件下轉速1000 r/min 時，不同潤滑膜厚度下固體顆粒沉積分布云圖。可以看出，隨著膜厚的增大，沉積區域明顯由槽內低壓區上游向背風側下游和外槽根側擴展，沉積量明顯增加。這進一步說明壓力梯度減弱的效應，此外，膜厚增大使進入潤滑膜的顆粒絕對數增多和沉積量增大。

圖15 顆粒進口體積分數對沉積率的影響Fig.15 Influence of particle import volume fraction on deposition rate

圖16 不同潤滑膜厚度下固體顆粒沉積分布Fig.16 Deposition distribution of solid particles under different thickness of lubricating film

圖17 潤滑膜厚度對沉積率的影響Fig.17 Influence of thickness of lubricating film on deposition rate

圖17為介質壓力0.2 MPa、顆粒直徑2 μm、進口顆粒積分數10%時不同轉速下顆粒沉積率隨潤滑膜厚度的變化規律。由圖17可知，沉積率隨著潤滑膜厚度的增大呈波動上升趨勢，轉速越低波動越明顯，沉積率上升也越明顯。這是因為隨著潤滑膜厚度的增加，潤滑膜壓力下降，高壓區與內外徑側的壓力梯度減小，固體顆粒從內外徑側逃逸的數量減少，導致沉積率呈上升趨勢，同時，由于膜厚增大，潤滑膜剛度和穩定性減弱，可能是沉積率出現波動的原因。

4 結 論

在本文研究的參數范圍內，經密封微間隙潤滑膜氣液固數值模擬分析得到如下結論。

（1）固體顆粒沉積率隨顆粒直徑的增大而明顯增大，隨轉速的增大而降低且粒徑越大下降越明顯，隨介質壓力的增大而降低且粒徑越大下降幅度越大，隨顆粒進口體積分數的增大而呈略顯下降趨勢，隨潤滑膜厚度的增大而呈波動上升趨勢且轉速越低上升越明顯。可見，粒徑較小、轉速增大、介質壓力增大、膜厚減小有利于降低顆粒沉積率。

（2）螺旋槽低壓區是固體顆粒沉積的主要部位，顆粒在螺旋槽內的沉積分布與粒徑、轉速、介質壓力、顆粒進口體積分數和膜厚等參數的大小密切相關，粒徑、顆粒進口體積分數、轉速和膜厚增大，介質壓力降低，會使沉積區域明顯向外槽根拓展，這是螺旋槽易出現堵塞失效的原因。

（3）低轉速時易在壩區出現顆粒沉積，且非槽區的沉積顆粒呈周向分布。

符 號 說 明

Cd——曳力系數

cp——固體顆粒質量體積濃度，kg/m3

dp——顆粒直徑，m

F——體積力，N

FP,FD,Fg,F離——分別為固體顆粒受到的壓強梯度力、繞流阻力、重力、離心力，N

h——密封間隙潤滑膜厚度，μm

hc——槽深，μm

mp——顆粒質量，kg

Ng——槽數

n——相數

rg——槽根圓半徑，mm

ri——螺旋槽內半徑，mm

ro——密封面外半徑，mm

u——流體速度，m/s

up——顆粒速度，m/s

vdr,k——第k相的漂移速度，m/s

vm——質量平均速度，m/s

α——螺旋角，(°)

αk——第k相的體積分數

β——槽徑比

γ——槽寬比

μm——混合黏性系數，Pa·s

ρ——流體密度，kg/m3

ρk——第k相的密度，kg/m3

ρm——混合密度，kg/m3

ρp——顆粒密度，kg/m3

φ——螺旋線展開角，(°)

ωp——旋轉軸角速度，rad/s