局部幾何構型對聚焦流微通道內液滴生成特性的影響

宋祺，楊智，陳穎，羅向龍，陳健勇，梁穎宗

（廣東工業大學材料與能源學院，廣東廣州510006）

引 言

液滴微流控技術是在微流控芯片基礎上發展起來的一種全新操縱微小液體體積的技術，該技術主要利用流動剪切力與表面張力之間的相互作用將連續流體分割分離成離散的納升級及以下體積的液滴[1]。與連續流技術相比，該技術具有諸多優點，如液滴體積小、試劑消耗減少、液滴樣品間無擴散、反應環境穩定、可避免樣品間的交叉污染等。因此，其在化學[2-7]、藥學[8-13]和生命科學[14-15]等諸多領域得到了廣泛應用。液滴微流控技術的核心是對微液滴的精確操控，而微液滴的生成是精確操控微液滴的前提。常見的生成微液滴的方式主要包括T型[16-18]、Y 型[19-22]、十字聚焦型[23-26]及同軸流[27-28]等微通道結構。與其他結構相比，十字聚焦型微通道內的液滴生成更易控制，液滴生成相對穩定、高效、均一度好，且液滴尺寸可調范圍更大，因此受到廣泛關注。

近些年來，針對十字聚焦微流控通道，不同學者基于實驗和數值模擬方法，分別研究了兩相流體物性（如表面張力、黏性系數）、流量比和通道幾何結構等參數對液滴生成的影響，并建立了一系列用于預測液滴生成尺寸的關聯式。Peng等[29]基于實驗和模擬方法的研究發現：隨表面張力的增大，液滴尺寸不斷增大，生成頻率不斷降低。Wu 等[30]利用VOF 方法模擬研究了流動聚焦微通道下游局部孔口結構對液滴尺寸、單分散性和液滴生成頻率的影響，發現液滴生成受孔口半徑的影響較大，而對孔口長度不敏感。此外，液滴生成頻率并不簡單地隨孔口半徑呈單調性變化，而是當孔口無量綱半徑*= 0.625 時達到最大值。Liu 等[31]利用格子Boltzmann 模擬方法研究了流量比、毛細管數和通道幾何形狀（寬度和深度）對液滴生成的影響，發現柱塞狀液滴長度與流量比呈線性關系，與毛細管數呈冪律函數關系，并提出了一種基于流體流量和通道幾何參數來關聯液滴長度的數學模型。Tan 等[32]采用實驗和數值模擬的方法，研究了下游主通道幾何形狀對液滴生成的影響，發現錐形擴張的幾何形狀有助于形成速度梯度，進而可實現液滴破裂位置的精確控制。Lashkaripour 等[33]針對具有下游擴張孔口的十字聚焦微通道，采用有限元模擬方法研究了液滴半徑隨流量比和毛細數的變化，發現毛細數和流量是影響液滴生成半徑的主要因素。Gupta 等[34]針對聚焦流通道，采用格子Boltzmann 方法模擬研究了低毛細數下孔口寬度、孔口長度和孔口入口距離對液滴形成機制和液滴生成大小的影響，發現聚焦型通道內液滴的擠壓階段比T 型通道更早開始，液滴尺寸隨孔口寬度和入口距離的增加而增加，而隨著孔口長度的增加，呈先減小后增大的變化趨勢。

綜上所述，目前有關十字聚焦微通道內液滴生成的研究主要聚焦于流量比、毛細管數、表面張力等流體的流動和物性參數，以及通道幾何結構參數，主要包含通道深度、下游孔口半徑、形狀和長度等對液滴生成特性的影響。此外，許多研究者在實驗中通常經驗上將分散相入口通過拉絲處理形塑成錐形結構[35-38]，以更好地實現液滴的可控制備。可見，目前文獻中仍少有分散相入口通道結構及其與下游孔口協同對液滴生成特性的影響的相關報道。在模擬方面，目前針對多相自由表面流的模擬主要有拉格朗日式的界面追蹤法（interface tracking）和歐拉式的界面捕捉法（interface capturing）。界面追蹤法直接通過標記點跟蹤界面的運動，如邊界積分法（BIM）[39-40]、有限元法（FEM）[41]和浸沒邊界法（IBM）[42]等；界面捕捉法則根據描述界面物理量的演化來間接模擬界面的運動，如緊致插值曲線法（CIP）[43]、水 平 集 方 法（level set）[44]，流 體 體 積 法（VOF）[45]等。盡管界面跟蹤法可實現對短暫的液滴破裂或融合過程的精確模擬，但對液滴破裂或融合之前或之后的動力學過程模擬比較困難[46]。相比于界面跟蹤法，界面捕捉法則無須頻繁對網格進行切割聯通操作。微通道內的液滴生成過程不僅包含界面的變形和破裂，還包含界面的流動，這使得界面捕捉法成為實現該模擬的最好方法之一。在界面捕捉法中，流體體積法（VOF）和水平集方法（level set method）具有廣泛應用，且在處理界面拓撲結構的變化方面優勢顯著[45-47]。其中VOF 方法具有良好的質量守恒性和簡單的界面拓撲處理，但由于該方法的體積分數是一個階躍函數，故很難獲得精確的曲率和光滑的界面物理性質[48-49]。而level set方法不需要重構界面，可以隱式地捕捉界面且函數始終是光滑的，易于處理復雜界面變形或拓撲結構改變；但該方法的對流方程不是基于保守形式，故存在質量損失的缺點[50-51]。為了克服它們各自的缺點，Sussman 等[52]提出了一種新的VOF 與level set 耦合方法。目前該方法已成功地應用于微通道中兩相流的模擬，并取得了較好的數值計算結果[53-55]。因此，本文將主要采用VOF/CSF 耦合level set 的數值模擬方法，深入研究分散相入口、下游通道孔口以及二者協同變化對液滴生成特性的影響，進而為十字聚焦通道內微液滴的生成特性提供更多的規律性認識，從而為后續實現液滴的精確調控提供重要指導。

1 幾何建模

圖1 為十字聚焦微通道的二維幾何結構，其中兩相入口夾角θ=90°，連續相和分散相入口段通道寬度為wc=wd=100 μm，兩相交匯處下游的孔口寬度和長度為wori= Lori= 50 μm。為保證兩相流動在下游微通道內充分發展，本文將出口段主通道寬度設為wo=100 μm，長度設為Lo=1250 μm。此外，本文選取硅油為連續相（其密度和黏性系數為ρc=965 kg/m3，μc=50 mPa·s），水為分散相（其密度和黏性系數為ρd= 998.2 kg/m3，μd= 1.005 mPa·s），兩相間表面張力系數為σ=30 mN/m。為確保不同結構通道內均有液滴生成，經過多次實驗，將連續相和分散相入口流速分別設定為vc= 0.03 m/s，vd= 0.05 m/s。

2 數學模型和可行性驗證

2.1 數學模型

假定兩相流體的密度和黏度為常數，因此可視為不可壓縮的各向同性牛頓流體，故描述其動量守恒的Navier-Stokes方程控制方程如下所示

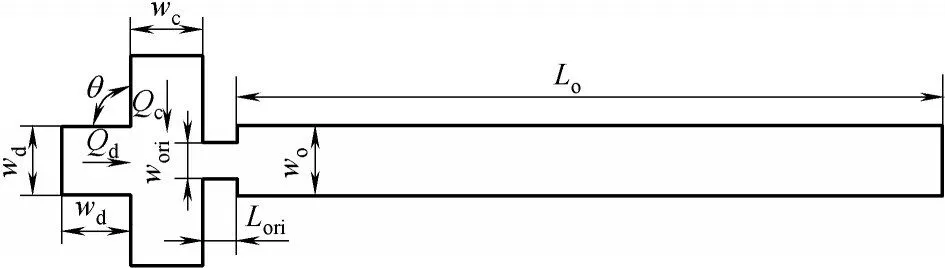
圖1 十字聚焦微通道二維幾何結構（下角標c和d分別表示連續相和分散相）Fig.1 Schematic diagram of 2D geometric structure of crossfocusing microchannel（subscripts c and d represent continuous and dispersed phase,respectively）

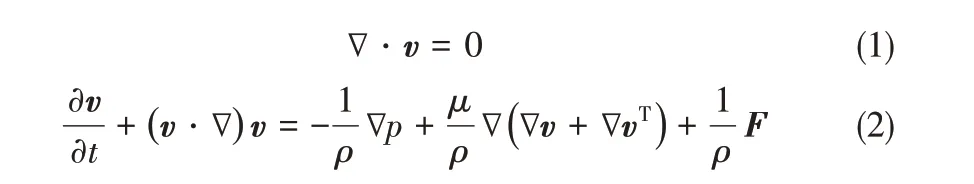
式中，v 是流體的速度矢量；t 是時間；p 為壓力；ρ 和μ 分別是流體的密度和動力學黏度；(v·?)v 為單位體積流體的慣性力；?p 是單位體積流體所受的壓強梯度；μ?(?v + ?vT)表示單位體積流體受的黏性力；F 為與表面張力相關的動量源項。

由于微通道內液滴的形成涉及復雜的界面演變過程，如生長、擠壓、破裂等過程，因此本文采用流體體積耦合水平集(VOF/CSF+level set)的界面顯示算法對兩相非混合界面進行捕捉。VOF 方法是通過計算每一個控制體積內連續相和分散相的體積分數來表征界面，如式（3）所示，其中κ 是界面曲率。假設計算的每個控制體積中分散相的體積分數為α，α = 1，表示該控制體內只含有分散相；α =0，則表示該控制體內不含分散相；0 ＜α ＜1，表示該控制體內有兩相交界面。在混合控制體積內，式（1）和式（2）中的兩相混合密度和黏度的計算可由式（4）和式（5）計算得到

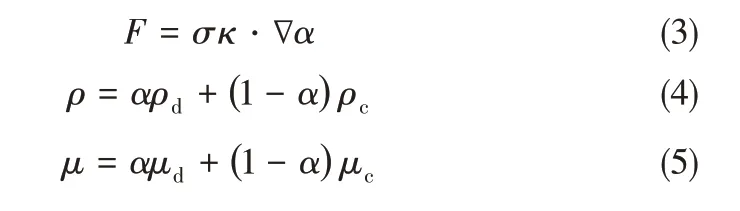
此外，每個控制體積內的體積分數α 可以通過求解一個（或多個）相的體積分數的連續性方程得到，如式（6）所示

level set 方法是把隨時間運動的物質界面看作某個函數φ(x,t)的零等值面，即在每個時刻t，只要求出函數的值就可知道其零等值面位置，也即運動界面位置。構造函數φ(x,t)，使得在任意時刻，運動界面Γ(t) 恰好是φ(x,t) 的零等值面，即Γ(t) ={x ∈Ω:φ(x,t)= 0}，這里要求φ(x,t)的初值滿足在Γ(t)附近為法向單調，在Γ(t)上為0, φ(x,0)取為x點到界面的符號距離函數，函數如式（7）所示

其中，d(x,Γ(0)) 表示x 到Γ(0)的距離函數；Ω1和Ω2分別表示第一種介質和第二種介質所在區域。由于在任意時刻t，φ(x,t)的零等值面就是活動界面，即Γ(t) = φ(x,t) = 0，所以函數φ(x,t) 應滿足式（8）

在十字聚焦微通道內流體Reynolds 數較小，因此采用層流模型。連續相和分散相的入口由體積分數定義，兩相入口速度均由常規速度定義，出口設定為具有101.325 kPa 的開口邊界條件。通道壁面設定為無滑移邊界條件。為了符合實驗中芯片材料PDMS 通道壁面的疏水特性，防止分散相浸潤通道壁面并保證液滴順利生成，本文將接觸角設定為135°。在Navier-Stokes 方程的數值求解中，采用SIMPLE 算法建立壓力速度耦合，選用PRESTO！算法為壓力插值方案。梯度計算采用least square cell based 方法，動量方程的空間離散化采用second order upwind，時間離散方式采用first order implicit。對于兩相界面附近的控制體積，選用geo-reconstruct用于界面插值。

2.2 網格無關性和可行性驗證

基于有限體積法（FVM）的數值模擬是基于網格進行迭代計算。通常在一定范圍內，網格越小，計算結果越精確；但網格越小，所消耗計算資源越大。為尋求最具經濟性的網格尺寸，本文采用四邊形結構化網格對十字聚焦通道的二維幾何模型進行網格劃分（圖2），分別選取了6 種尺寸(3 μm × 3 μm、2.5 μm× 3 μm、2 μm× 3 μm、2 μm× 2.5 μm、2 μm× 2 μm、2μm × 1.5 μm) 的網格單元來進行網格無關性驗證，結果如圖3 所示。當網格單元尺寸分別為2μm × 2 μm 和2 μm× 1.5 μm 時，液滴生成周期無明顯差異，可視為網格大小對模擬結果的影響近似收斂。因此，為兼顧計算結果的準確性和計算成本，后續模擬中的幾何通道均選用2 μm× 2 μm網格單元進行網格劃分。

圖2 數值模擬過程中網格無關性驗證Fig.2 Grid independence validation

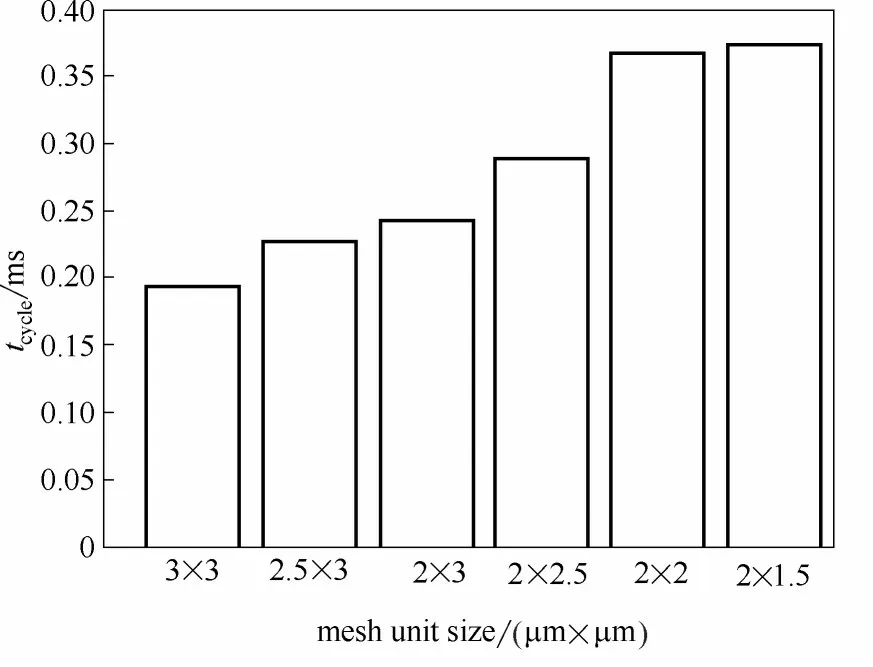
圖3 不同網格所對應的液滴生成周期Fig.3 Droplet generation cycles for different grids

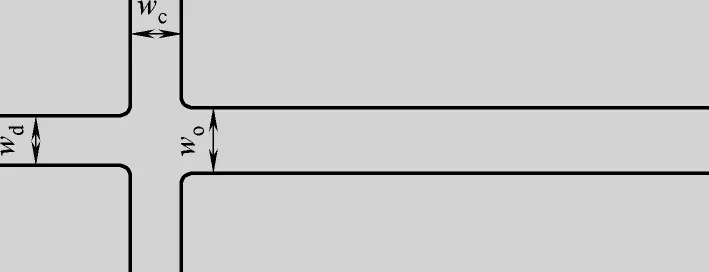
圖4 實驗通道結構Fig.4 Schematic diagram of experimental channel structure

此外，為驗證模擬方法的可行性，模擬條件的設置與實驗相同，即兩相入口寬度均為wc= wd=100 μm，出口段主通道寬度為wo= 130 μm，如圖4所示，連續相和分散性流量分別為Qc= 120 μl/h，Qd=60 μl/h，實驗中十字聚焦通道內生成的液滴采用高速攝像儀進行拍攝，進而將模擬與實驗結果在相同尺度下進行對比，如圖5(a)、(b)所示。可見，實驗獲取的分散相液滴曲率和模擬獲得的曲率極為相近。為了進一步驗證模擬方法的可行性，本文固定分散相流量Qd=50 μl/h，將連續相流量從20 μl/h逐漸增大到70 μl/h，并將模擬和實驗所獲得的液滴直徑進行對比，如圖5(c)所示。考慮到實驗通道壁面親疏水特性不均一及兩相在聚焦前存在的動量損耗等原因，模擬與實驗結果總體上具有較好的一致性。

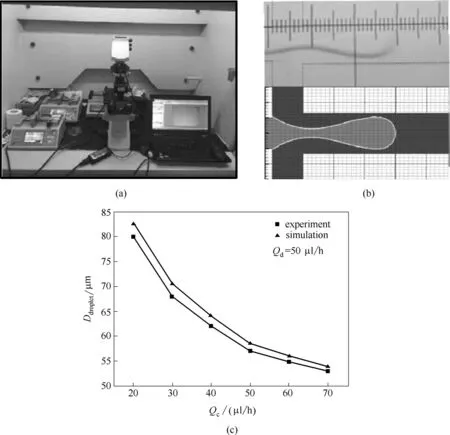
圖5 液滴生成的模擬與實驗結果對比Fig.5 Comparison of droplet morphology between simulation and experiment

3 結果與討論

3.1 孔口寬度對液滴生成的影響

圖6 不同孔口寬度下液滴斷裂時刻的兩相云圖Fig.6 Two-phase cloud diagrams at droplet break-up under different orifice widths

分散相和連續相入口通道夾角θ=90°，孔口長度Lori= 50 μm，其他參數與圖1 設置相同。為研究孔口寬度對液滴生成的影響，本文將孔口寬度wori分別設置為50、65、75、85、100 μm，不同孔口寬度通道內液滴破裂時刻的兩相云圖及液滴生成周期tcycle和直徑Ddroplet分別如圖6 和圖7 所示。由圖6 可知，隨孔口寬度的收縮，液滴生成直徑和周期逐漸減小，圖7顯示液滴生成直徑和周期與孔口寬度呈近線性正相關。

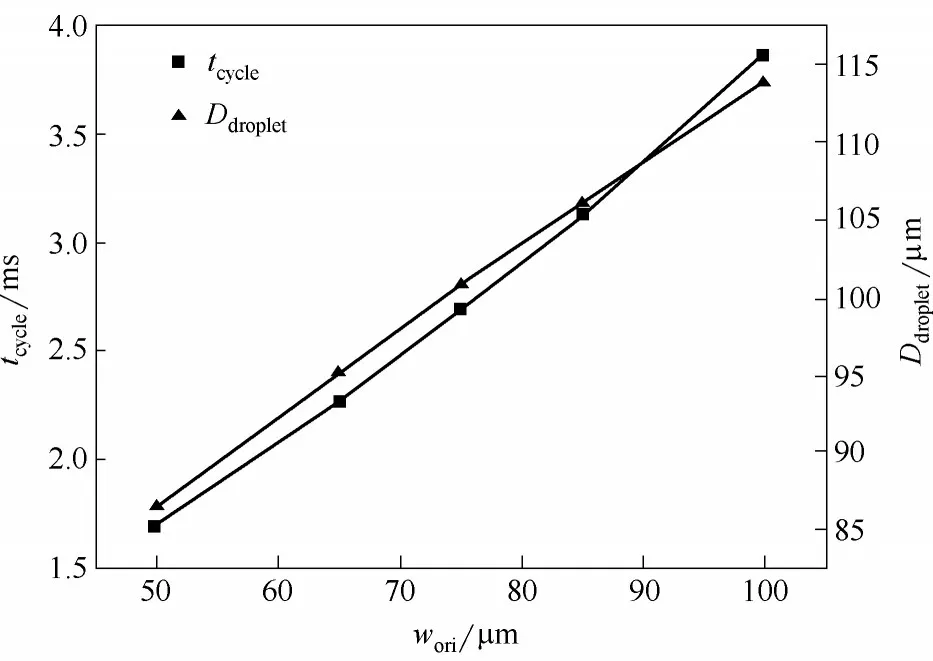
圖7 液滴生成周期tcycle和直徑Ddroplet隨孔口寬度的變化Fig.7 Variation of droplet formation cycle and diameter with orifice widths

圖8 各監測點速度隨孔口寬度的變化Fig.8 Velocity component of each monitoring point varies with orifice widths

為揭示其內在的動力學成因，本文選取了位于兩相流交匯區內的a、b 兩點[如圖8（a）所示，a 點坐標(150 μm，0 μm)，b點坐標(150μm，40 μm)]，并進行監視。隨孔口寬度的逐漸減小，圖9(a)中b點的Y方向速率|vb,y| 在整個周期內的平均值逐漸增大，圖9(b)中a 點X 方向速率|va,x|在t3～t4時間段內以更大的加速度加速至最大值。可見，孔口的收縮阻礙了連續相下游方向的移動，也因此強化了連續相Y 方向的速度動量，即強化了對液滴豎直方向的擠壓作用。

在對點a和b的監測中發現，各點單個周期的X或Y方向速度分量在不同通道內均呈現出類似的波動變化，如圖9(a)、(b)所示。為闡明該波動性變化，本文在圖9(a) 中對wori= 50、100 μm 兩通道內的vb,y曲線轉折點（ta1～ta5，te1～te5）進行了標示，顯然vb,y在相鄰兩點的時間區間內均呈單調性變化，且各時刻點所對應的液滴生成輪廓及速度與壓力場如圖9(c)所示。結合圖9(a)、(c)可知，在t1～t2區間內，界面張力占主導作用下的液滴回彈使得vb,y急劇減小；在隨后的t2～t3區間內，液柱前沿的持續回彈進而減小了連續相向下游的流動阻礙，vb,y也開始逐漸增大。在t3～t4區間內，液滴的回彈及分散相持續流入的共同作用使得液柱體積逐漸膨脹，且其邊界逐漸向b 點趨近，使得vb,y開始逐漸減小；此間，液柱前沿略微向下游延伸。從t4時刻開始，b 點正下方的液柱寬度在達到最大值后開始持續收縮，這主要由于液柱前沿持續向下游移動，使得連續相的流動空間逐漸被分散相所占據，也即等效于通道截面的收縮促使了vb,y的持續增大，其對液柱Y 方向的擠壓作用（黏性正應力）也得以強化，從而促進了b 點正下方液柱寬度的持續收縮直至液滴破裂。總體而言，孔口的收縮減少了連續相的流通截面面積，連續相在孔口處的動量因此得以強化，這反過來促進了其對液柱在Y 方向的擠壓和X 方向的黏性剪切拖拽作用。

為了更嚴格地闡明孔口影響液滴生成的作用機制，本文進而基于可比性原則，聚焦于不同通道內處于相同頸部寬度(Wneck=20 μm）的分散相液柱[圖9(d)]，并對此時通道內b 點的Y 方向速度分量大小|vb,y| 進行了對比，如圖8（b）所示。結果顯示，孔口寬度逐漸增大，|vb,y|逐漸減小，也即連續相Y 方向對液滴的黏性正應力μ ?vy?y 逐漸減小，液滴在形成過程中受連續相的擠壓作用逐漸減弱，從而導致液滴生長和擠壓階段所經歷的時間隨著孔口寬度增大而持續增加[如圖10 所示，圖10（a）中曲線對應于液滴生成的擠壓階段，曲線終點為液滴斷裂時刻，也即液滴生成周期]。

圖10（a）顯示了不同孔口通道內液滴頸部寬度Wneck和位置Xneck隨時間的變化。可見，隨時間的推移，Wneck不斷減小，Xneck呈先減小后增大的變化趨勢，且在圖10（a）中所示的t2～t3階段發生轉折。圖10（b）中的相圖顯示，液滴頸部寬度均在孔口入口處開始形成，此后頸部不斷被擠壓，頸部下游液柱不斷膨脹，頸部位置逐漸向上游移動。當頸部位置移動至轉折點t2處，也即最小X 坐標位置，頸部位置在隨后相當長的時間內（t2～t3）保持不變。

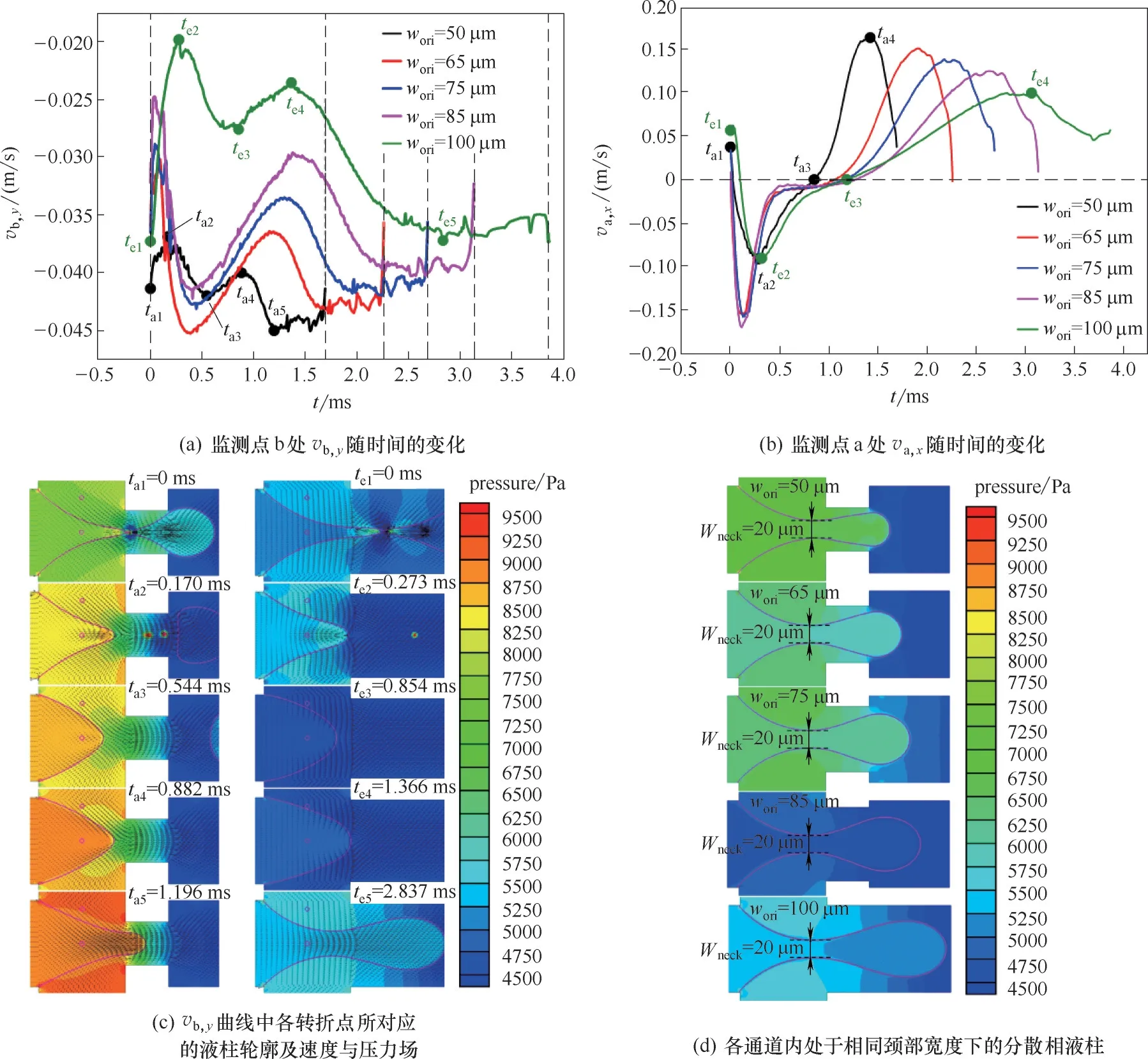
圖9 單個生成周期內監測點速度、液柱輪廓、速度場和壓力場隨時間的變化Fig.9 Monitoring velocity,droplet profile and velocity and pressure field in a single cycle

然而，圖10（a）顯示，孔口寬度越大，液滴頸部可在固定的最小X坐標位置處持續被擠壓的時間越長，也即時間段t2～t3越長。這主要由于孔口寬度越大，連續相向下游流通的阻礙越小，其對分散相的黏性拖曳和擠壓作用相對較弱，頸部下游液柱在表面張力作用下顯著膨脹，同時流經頸部的分散相流體速度也相對較小，二者的協同作用在一定程度上抑制了液滴頸部向下游移動的趨勢。此外，頸部收縮率隨孔口寬度的增大而不斷減小，且在最小X 坐標位置區間內（t2～t3），頸部呈近線性收縮。隨著頸部持續收縮，頸部內部分散相流速不斷增大，同時頸部收縮阻礙了來流分散相的流動，導致頸部上游局部壓力增大，當壓力增大至某一臨界值時，頸部位置開始向下游移動（t3～t4），也即在整個液滴擠壓破裂過程中，頸部位置呈階梯型變化。

3.2 豎直邊錐形角對液滴生成的影響

在微流控液滴生成實驗中，盡管很多研究通常從經驗上將分散相入口經過拉絲處理形成錐形結構，但該結構對液滴生成的影響卻少有研究。因此，這也是本文研究的主要動機。首先，保持錐形入口直徑不變（或三角形豎直邊長度不變Lver= 30 μm），將三角形斜邊與豎直邊的夾角θ1分別設置為20°、30°、40°、50°、60°和70°，其通道結構及液滴破裂時的相圖如圖11 所示。此外，液滴生成周期tcycle和直徑Ddroplet與θ1的對應關系如圖12所示。

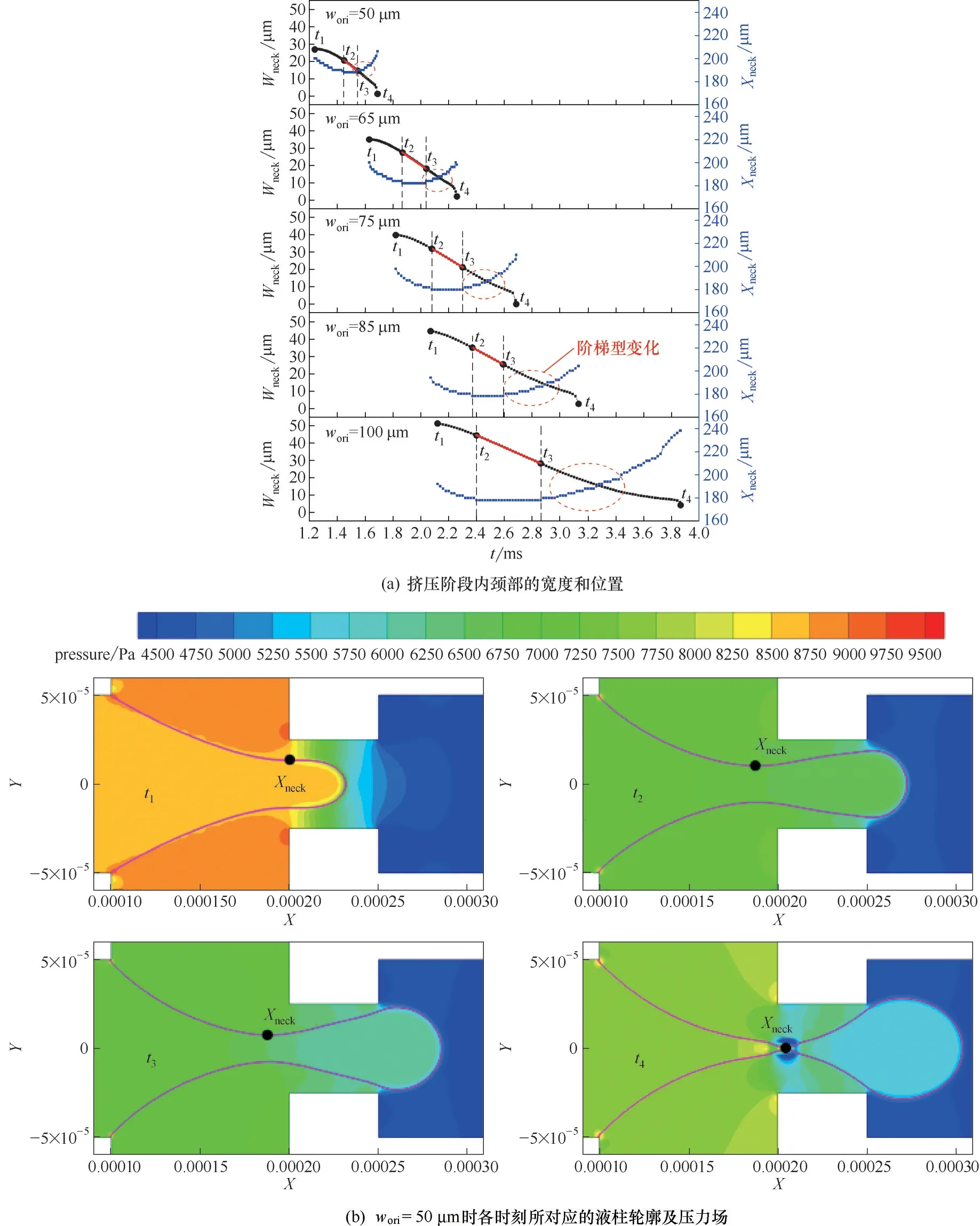
圖10 擠壓階段內頸部寬度和位置隨時間的變化Fig.10 Variations of neck width and position in squeezing stage

當孔口寬度為50 μm，豎直錐形角θ1由20°增大至40°時，液滴生成周期和直徑逐漸減小；而當θ1繼續由40°增大至70°時，液滴生成周期和直徑呈增大趨勢。為解釋其內在的動力學成因，本文對位于兩相交匯區內的c 點進行監視[c 點坐標(120 μm，0 μm)，如圖13（a）所示]。當液滴斷裂時，不同通道內c 點X 方向速度大小|vc,x|的對比如圖13（b）所示，錐形入口的局部速度場如圖14所示。結果顯示，錐形角連接處有回流形成，且當θ1由20°增大至40°時，回流區域及強度逐漸增大，從而削弱了分散相來流的動量，流入交匯區的分散相液柱也更易受到連續相的剪切作用，液滴生成周期因此持續減小。當θ1由40°增大至70°時，錐形角交匯處的回流區域及強度變化相對較小，但入口截面面積的減小更為顯著，因此對分散相具有更強的聚焦作用，也即分散相在兩相交匯處的X 方向速度逐漸增大，液滴生成周期隨之持續增大。

圖11 不同豎直邊錐形角下液滴斷裂時刻兩相云圖Fig.11 Two-phase cloud diagrams at droplet break-up under different θ1

圖12 液滴生成周期tcycle和直徑Ddroplet隨豎直邊錐形角的變化Fig.12 Variation of droplet formation period and diameter with θ1

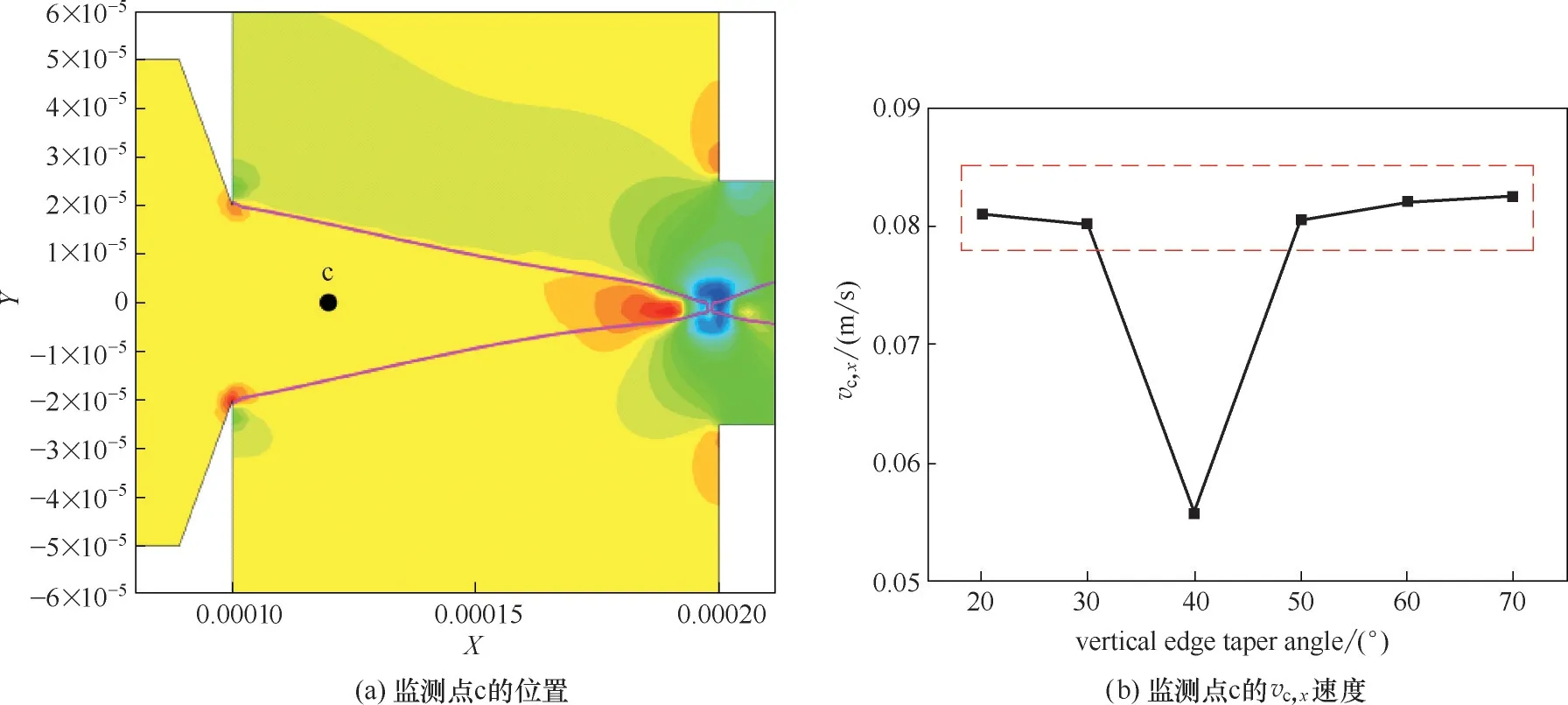
圖13 兩相交匯區內c點vc,x速度隨豎直邊錐形角的變化Fig.13 Variation of vc,x for different θ1

圖14 液滴斷裂時刻錐形入口的局部速度場分布圖Fig.14 Local velocity field of taper inlet at droplet break-up

盡管液滴的生成周期和直徑隨θ1的增大呈先減小后增大趨勢，但整體上，改變θ1對液滴生成周期（1.526～1.588 ms）和直徑（83.5～84.7 μm）的影響并不大，這主要由于不同的錐形角通道均具有相同的錐形入口寬度。

3.3 水平邊錐形角對液滴生成的影響

當錐形角水平邊長度恒定Lhor= 50 μm，將水平邊與斜邊的夾角θ2分別設置為0°、10°、20°、30°和40°時，不同水平邊錐形角結構下液滴破裂時的相圖及液滴生成周期tcycle和直徑Ddroplet分別如圖15 和圖16所示。整體上看，盡管θ2的變化會引起液滴生成周期的波動性變化，但對應液滴生成周期和直徑的影響范圍相對較小，1.562 ms≤tcycle≤1.716 ms，84.2 μm≤Ddroplet≤86.9 μm。然而，圖15 顯示不同錐形角θ2對應了交匯區內液柱輪廓的明顯變化。因此，液滴生成對錐形角θ2不敏感的原因可能在于：相對于錐形角θ2，較小的孔口寬度（wori= 50 μm）對液滴生成特性的影響更為顯著。

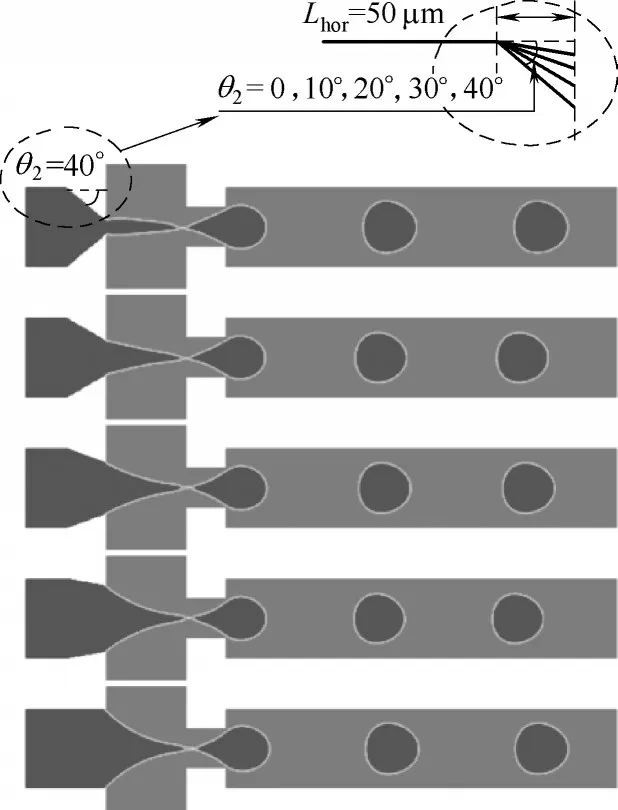
圖15 不同水平邊錐形角下液滴斷裂時刻兩相云圖Fig.15 Two-phase cloud diagrams at droplet break-up under different θ2

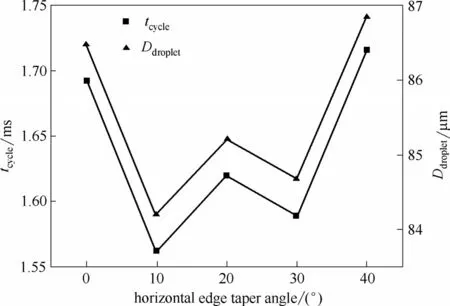
圖16 液滴生成周期tcycle和直徑Ddroplet隨水平邊錐形角的變化Fig.16 Droplet formation period and diameter for different θ2

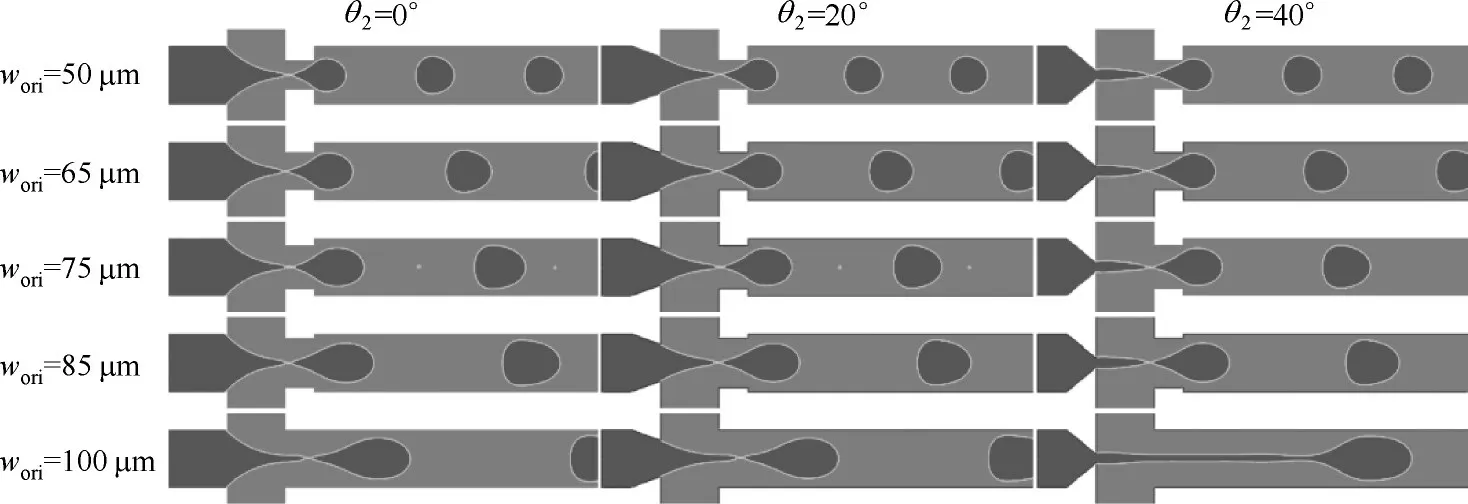
圖17 不同水平邊錐形角和孔口寬度下液滴斷裂時刻兩相云圖Fig.17 Two-phase cloud diagram at droplet break-up under different θ2 and wori

為進一步探究wori和θ2對液滴生成的協同影響，本文進而模擬并對比了15 個不同通道構型內的液滴生成特性，其中θ2分別設置為0°、20°和40°，wori分別設置為50、65、75、85、100 μm，同時對位于兩相交匯區內的a點進行監視。各通道構型內液滴破裂時的相圖及液滴生成直徑和周期分別如圖17 和圖18所示。顯然，當wori= 50 μm 時，改變θ2的角度對液滴生成的影響相對不顯著；然而，當wori=100 μm時，θ2的增大使得液滴生成模式由滴流向射流轉變；這也表明：液滴的生成明顯受到wori和θ2的共同影響，只是當wori較小時，孔口對液滴生成的影響更顯著。

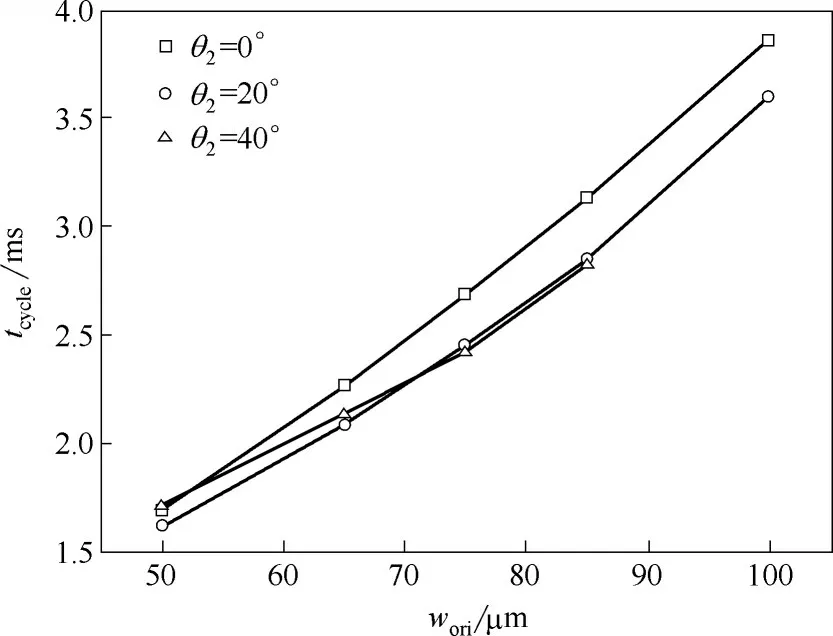
圖18 液滴生成周期tcycle隨水平邊錐形角和孔口寬度的變化規律Fig.18 Variation of droplet formation period under different θ2 and wori

此外，圖18 顯示：當wori= 50 μm 時，θ2= 20° 所對應的液滴生成周期比θ2= 0° 和40°時相對較小，也即液滴生成周期與θ2并非呈單調的函數變化關系；而當wori=75、85 μm時，θ2=40°所對應的液滴生成周期最小且與θ2=20°極為相近。為探究其內在的動力學成因，本文對比了不同通道內流體流經a點的X 方向速度(va,x)隨時間的變化，如圖19所示，發現隨著孔口寬度的增大，相同錐形角通道內液滴分散相的流速不斷減小。其中，t1～t2為液滴的生長階段，t2～t3為液滴的擠壓破裂階段。

圖19 單個生成周期內監視點a處不同水平邊錐形角下va,x速度隨時間的變化Fig.19 Change of va,x in a single generation cycle at different θ2

由表1可知：當wori=50 μm 時，不同錐形角θ2對液滴擠壓階段所消耗時間的影響相差不大，且在整個生成周期內占比相對較小，分別為26.757%、26.280%和24.753%，表明在液滴生成過程中，較小的孔口對分散相產生了較強的聚焦效應，因此液滴能在相對較短的時間內擠壓破裂。此外，wori= 50 μm時，錐形角θ2的變化對液滴生成周期影響較為微弱，表明孔口寬度對液滴形成起主要影響。當wori=75 μm 時，不同錐形角θ2對液滴擠壓階段所消耗時間在整個生成周期內占比分別為32.427%、31.679%和16.041%，可見錐形角θ2=0°，20°對液滴擠壓階段所消耗時間的影響相差較小，但與wori=50 μm 時相比，其在整個液滴生成周期內占比增大，表明孔口的聚焦作用相對減弱；而θ2= 40°時，液滴擠壓階段所消耗時間顯著縮短，表明在該通道構型情況下，較大的錐形角開始顯著影響液滴的生成特性。當wori=100 μm時，θ2=0°，20°時，通道內液滴呈滴流模式；當θ2增大至40°時，由于錐形角對分散相產生相對較強的聚焦作用，使得通道內分散相流動呈射流模式。在滴流模式下，θ2=0°，20°時，液滴擠壓破裂階段耗時占比進一步增大，分別為45.148%、47.532%，這表明當wori= 100 μm 時，孔口對連續相的聚焦作用進一步減弱。由此可見：較小的孔口可對連續相產生較強的聚焦作用，從而強化其流動剪切作用，此時錐形角的變化對液滴生成的影響相對較弱；當孔口寬度較大時，連續相的聚焦也持續減弱，此時錐形角對分散相的聚焦作用可顯著影響液滴的生成特性。

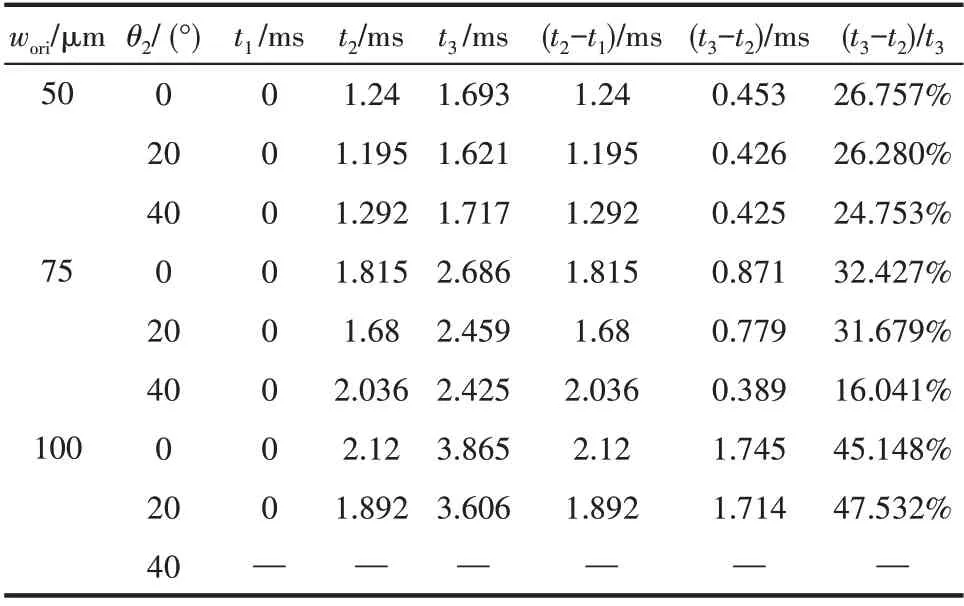
表1 不同通道構型下液滴生長與擠壓破裂階段所經歷時間的對比Table 1 Comparison of droplet growth and squeez fracture under different channel configurations

4 結 論

在微流控技術中，微通道結構的優化設計是一種被動實現液滴精確調控的有效方法。本文采用VOF/ CSF 耦合level set 的方法數值模擬了聚焦流通道局部幾何構型，包括分散相入口、通道下游孔口以及二者共存模式下的通道結構變化對液滴生成特性的影響，具體結論如下。

(1)在十字聚焦型微通道內，下游孔口寬度的收縮，使得連續相的流通截面面積相應減小，連續相在孔口處的動量因此弱化，即削弱了連續相對分散相液柱在Y 方向的擠壓和X 方向的黏性剪切拖拽作用，導致液滴生成周期和直徑隨著孔口寬度wori呈近線性變化。此外，頸部寬度的收縮速率隨孔口寬度wori的增大而不斷減小，孔口寬度越大，液滴頸部在頸部位置轉折點處的擠壓時間越長，且在轉折點處的擠壓過程中，頸部寬度呈近線性收縮。

(2) 當wori= 50 μm 時，豎直邊錐形角θ1由20°增大至40°時，液滴生成周期和直徑逐漸減小；而當θ1繼續由40°增大至70°時，液滴生成周期和直徑呈增大趨勢。但整體上，液滴生成周期和直徑對豎直邊錐形角θ1的變化不敏感，這主要由于不同的錐形角θ1通道均具有相同的錐形入口寬度。因此，在該孔口寬度條件下，改變θ1難以實現液滴生成周期和尺寸的有效調控，但這可為以后通道結構的設計提供重要參考。

(3)當孔口寬度較小（wori=50 μm）時，液滴生成對錐形角θ2的變化同樣不敏感，這主要由于孔口較強的聚焦效應主要影響液滴生成。而當孔口寬度較大（wori=100 μm）時，改變水平邊錐形角θ2，液滴生成周期和直徑隨θ2的增大而增大，液滴流型可由滴流向射流模式轉變，表明水平邊錐形角對分散相的聚焦作用對液滴生成開始發揮主要作用。

(4)微通道內液滴的生成受分散相入口錐形角和孔口寬度的協同影響，且當孔口較大時，入口錐形角可作為對液滴尺寸進行微調的一種有效手段。此外，當其他條件不變，且通道內分散相流型為射流時，縮小通道的孔口寬度即可對射流模式加以抑制。而當通道內分散相流型為滴流時，為獲取更大的液滴尺寸，宜選擇孔口寬度和分散相入口錐形角較大的微通道。

符 號 說 明

Ddroplet——液滴直徑，μm

Lhor,Lver——分別為錐形角水平邊、豎直邊長度，μm

Lo——出口段主通道長度，μm

Lori——孔口長度，μm

Qc,Qd——分別為連續相、分散相流量，μl/h

t——時間，ms

tcycle——液滴生成周期，ms

va,x,vc,x——分別為監測點a、c在X方向速度，m/s

vb,y——監測點b在Y方向速度，m/s

vc,vd——分別為連續相、分散相速度，m/s

Wneck——頸部寬度，μm

wc,wd——分別為連續相、分散相入口段通道寬度，μm

wo——出口段主通道寬度，μm

wori——孔口寬度，μm

Xneck——頸部位置，μm

θ——兩相入口夾角，(°)

θ1——三角形斜邊與豎直邊夾角，(°)

θ2——三角形斜邊與水平邊夾角，(°)

μc,μd——分別為連續相、分散相黏度，mPa·s

ρc,ρd——分別為連續相、分散相密度，kg/m3

σ——表面張力系數，mN/m