流動聚焦微通道內牛頓微液滴在冪律剪切致稀流體中的生成研究

陳琦，李京坤，宋昱，何倩，David M Christopher，李雪芳

（1 山東大學熱科學與工程研究中心，山東濟南250061； 2 清華大學能源與動力工程系，北京100084）

引 言

微流控技術是指在微米尺度對流體進行操控的一種技術，它可以將生物、化學實驗室微縮到一個幾平方厘米的芯片上。微流控液滴技術是其中的一個重要分支，它利用兩種互不混溶流體間的相互作用將離散相分割成多個微小體積的液滴，并使其分散在連續相之中。微流控液滴技術具有以下優勢：（1）液滴被連續相包覆，樣品無擴散，濃度和反應環境穩定，可以避免交叉污染；（2）液滴體積小，試劑消耗少，可以減少來源少、價格昂貴試劑的使用；（3）液滴比表面積大，反應時間短，具有較高的傳熱傳質效率；（4）可以實現液滴的精準控制和快速批量生產，生產速率可以達到十幾千赫[1-2]。

自從Thorsen 等[3]提出使用T 型微通道來生產單分散液滴以來，大量的研究者開始關注和研究這種新型的液滴生成方式。微通道中的兩相流動是微流控液滴技術的基礎，研究內容涉及流型、生成動力學及參數預測等。研究表明，微通道中兩相流動有三種基本流型：擠壓狀[4]、滴狀[5]和射流狀[2，6]。Xu等[7-9]發現只有當離散相流體與通道壁面間的接觸角大于90°時才能生成規則液滴，否則只會形成兩相液膜，液滴的大小與兩相流率、黏度和界面張力等因素有關。Anna等[10]在T型通道的基礎上提出使用流動聚焦微通道來進行液滴制備，相比T型通道，它可以更高頻率地制備體積更小的微液滴，但該方式原理更復雜，液滴大小和頻率更難以控制。

近年來，隨著微流控技術在化工、生物及醫學等領域內的廣泛應用，研究開始向使用非牛頓流體作為離散相或連續相的方向發展。Fu 等[11]研究了聚焦通道中微氣泡在剪切致稀流體中的破碎機制，表明連續相的流變特性會對微氣泡的破碎形態和氣泡大小產生顯著影響，并給出了相應的預測模型。Rostami 等[12]觀察了硅油連續相中牛頓和非牛頓液滴的生成過程，研究了黏度比和離散相的流變特性對液滴狀態及流型的影響，發現離散相的非牛頓特性也會明顯影響微液滴的生成。張沁丹等[13]對流動聚焦通道內液滴在黏彈性流體中的生成進行了實驗研究，發現液滴尺寸隨連續相流率、毛細數及彈性數的增加而減小，隨離散相流率的增加而增加，連續相彈性對液滴尺寸的影響相對較小，并在此基礎上建立了液滴尺寸的預測關聯式。Sontti等[14]和Shi等[15]針對T型微通道內冪律流體中的微液滴生成進行了數值模擬，研究了冪律流變參數對微液滴生成的影響。然而，T 型通道和流動聚焦通道內液滴或氣泡的生成原理不盡相同，流動聚焦通道內以非牛頓流體作為連續相或離散相的研究仍不完備。

盡管在微流控液滴技術領域內已有眾多研究，但涉及非牛頓流體的研究仍然偏少，不同研究者所得的結論也不盡一致，缺少公認的預測液滴生成尺寸、頻率等重要特征參數的模型。本文采用開源CFD 軟件OpenFOAM 模擬了微通道內牛頓流體的兩相流動和冪律剪切致稀流體單相流動，通過與實驗數據對比驗證了模型的準確性。以此為基礎計算了硅油微液滴在冪律剪切致稀流體中的形成過程，研究了連續相流變參數對微液滴破碎機制、生成尺寸和頻率等的影響。研究結果對臨床使用過程中冪律流體中微液滴制備和微通道設計具有一定的指導意義。

1 控制方程

1.1 連續性及動量方程

由于兩相流動的復雜性，模擬做出如下假設：兩相流體在微通道內表現為層流流動；流體均視為不可壓縮流體且與外界不存在熱交換；流動過程中起主導作用的是黏性力和界面張力，忽略重力作用。界面張力作為一個源項引入動量守恒方程。因此，連續性方程和動量方程可分別表示為

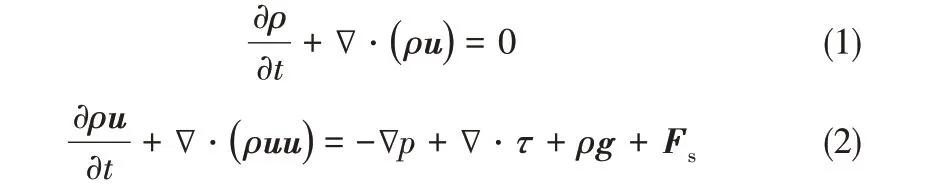
界面張力只作用于兩相界面處，采用CSF 模型（continuum surface force）[16]進行計算

模擬通過定義壁面處的靜態接觸角（θw）考慮了壁面的潤濕特性，壁面附近網格單元的界面法向量表示為[17]

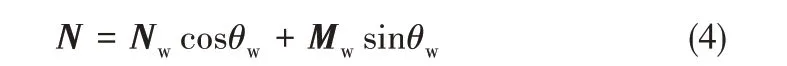
本文假設壁面被連續相完全潤濕，設置連續相的壁面接觸角為0°。

流動過程中的黏性剪切應力可表示為

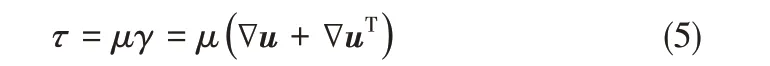
對于牛頓流體，其黏度為常數，黏性剪切力與剪切率呈正比。參考牛頓流體，定義了非牛頓流體的表觀黏度為μ(γ)。本研究所用的冪律模型的本構方程為

當n ＜1 時表示剪切致稀流體，n = 1 時表示牛頓流體，n ＞1時表示剪切致稠流體。

1.2 VOF模型

相界面的捕獲通過定義一個相分數α 來實現，α = 1 表示網格單元全部被離散相占據；α = 0 表示網格單元全部被連續相占據；0 ＜α ＜1 表示兩相界面。在計算過程中，式(1)和式(2)中的密度和黏度均為混合屬性，并通過式(7)和式(8)計算

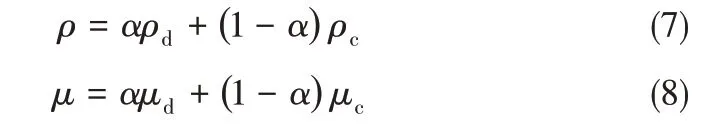
兩相體積分數α可通過式(9)計算獲得

在VOF 模型中，相分數α 作為一個特殊的被動標量，數值上必須保證在0 ≤α ≤1 范圍內。而在現實中，相分數應該只存在兩個數值：0 和1。這種計算方法中，0 ＜α ＜1 的情況會導致相界面模糊。為了使相界面更加清晰，采用OpenFOAM 開發的界面壓縮方法對VOF模型進行了優化[18]。通過引入一個人工對流項對相界面處的相分數進行壓縮，以限制這種界面模糊性。添加人工對流項后，式(9)可表示為

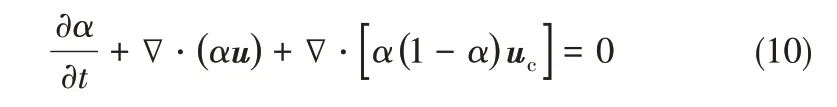
式(10)左邊第三項即為人工添加的壓縮項，在非界面處為0[19]。uc為需要模化的速度，為了不改變界面的位置，壓縮效果只作用在界面的法向上，因此其方向與界面法向量同向，最大值不超過u。為了確保相界面位置不發生改變，Weller[20]提出uc可表示為

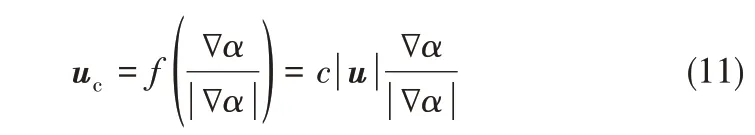
其中，c 為可控壓縮因子，當c = 0 時無壓縮效果，c 越大壓縮效果越明顯。本文選取c= 1 進行界面壓縮。該方法相比傳統的PLIC 等界面重構方法[21]，可以節省更多的計算資源。

1.3 離散格式

模擬全部采用interFoam 求解器進行，壓力-速度耦合采用PISO 算法。表1 列出了控制方程各項的離散格式。為了保證計算的穩定性和收斂性，模擬采用自適應時間步長，即在每次迭代開始時，根據庫朗數計算一個新的時間步長。本研究設置模擬最大庫朗數為0.5。

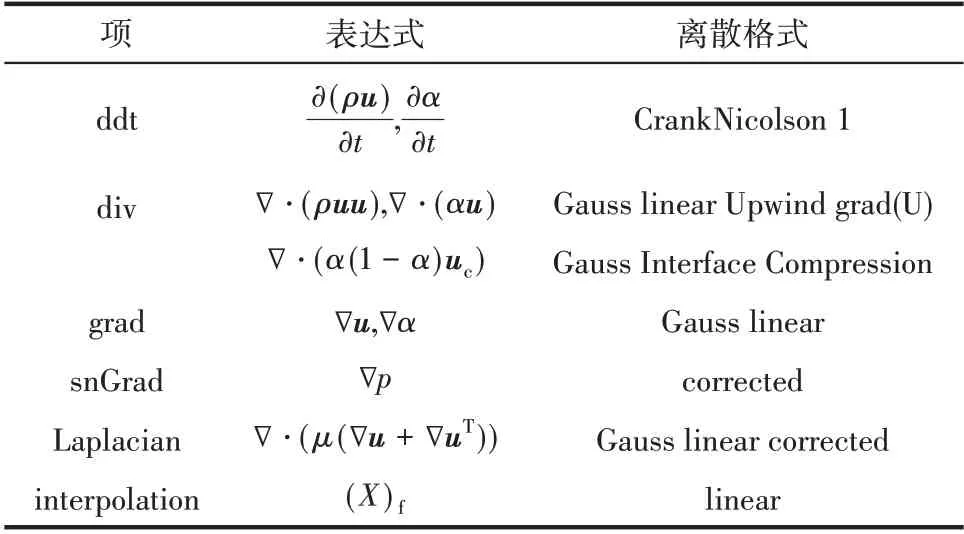
表1 方程各項離散格式Table 1 Discretization schemes for different terms of governing equations

2 模型構建

三維流動聚焦微通道的幾何模型如圖1 所示，通道截面為正方形，寬度為0.6 mm。為了保證流動在交叉處達到充分發展狀態，采用式(12)計算了層流狀態下的入口段長度[22]

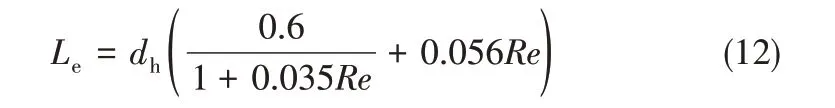
由于微通道特征尺寸較小，本研究中流動的Reynolds 數在10-2數量級，入口段長度約為通道水力直徑的0.6 倍。因此，模型設置交叉口上游段長度為1.8 mm，下游段長度為18 mm。微通道內流動為典型層流流動，采用正方體網格對整個計算域進行離散。液滴的無量綱長度（液滴長度L 與通道寬度Wc的比值）隨網格間距的變化如圖2所示，當單個網格邊長低于24 μm 時，進一步細化網格對計算結果基本無影響。

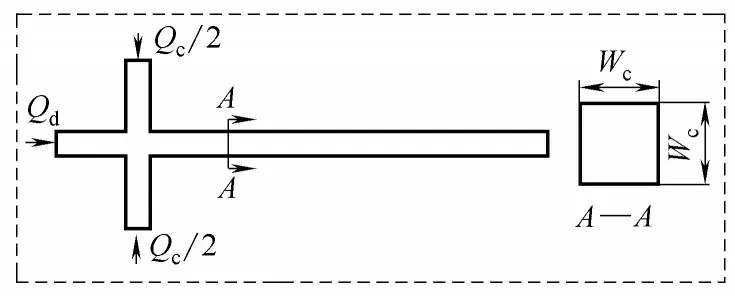
圖1 流動聚焦型微通道幾何模型Fig.1 Geometry of flow-focusing microchannel

離散相流體以恒定流率Qd從通道左側流入，冪律剪切致稀流體作為連續相以Qc/2的流率從通道的兩側流入。模擬選取的流體屬性如表2 所示，對于所有參數的冪律剪切致稀流體，流體黏度均隨著剪切率的增大而減小。且在低剪切率下，黏度變化較大；在高剪切率下，黏度基本不發生改變。壁面采用無滑移邊界條件，壁面處壓力梯度為0，出口為大氣壓。

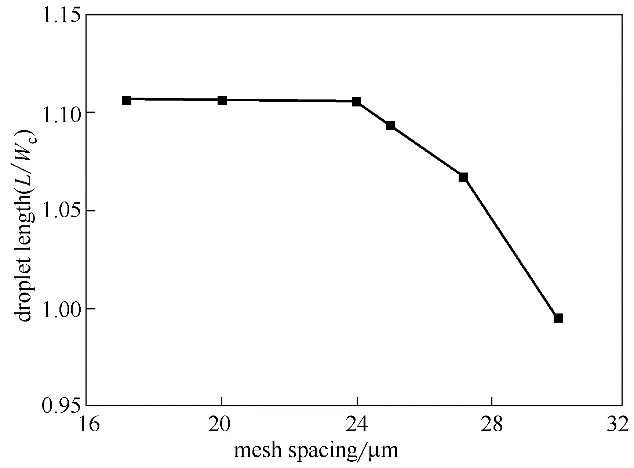
圖2 網格獨立性驗證Fig.2 Mesh independence validation

表2 兩相流體屬性設置Table 2 Physical properties of two phases

3 結果與討論

3.1 模型驗證

3.1.1 VOF 模型驗證 為驗證interFoam 求解器的準確性，參考Fu 等[23]的微液滴破碎實驗條件進行了數值模擬，液滴生成過程如圖3 所示。離散相為硅油，連續相為去離子水，分別以Qd= 300 μl/min 和Qc=2000 μl/min的流率從通道入口流入。液滴的整個生成周期與脫離形態與實驗結果基本一致。此外，在液滴脫離后的初始階段均觀察到了衛星液滴的存在，由于衛星液滴移動速度較快，在18 ms 左右與主液滴接觸并融合。由于實驗中各種不確定性因素的影響，如流體屬性及流率的測量偏差、溫度、壁面粗糙度及潤濕特性等，計算結果和實驗結果存在一定的偏差，且在微尺度條件下這些因素的影響更加顯著。此外，拍攝條件也會對實驗結果產生影響，當氣泡移動速度較快且相機拍攝的快門速度不夠時會造成拍攝所得的氣泡圖像周圍存在一層拖影，從而造成拍攝到的尺寸大于實際氣泡尺寸。對比實驗和模擬結果，發現模擬得到液滴的移動速度稍大于測量值，這主要是實驗中壁面摩擦力的存在造成的。

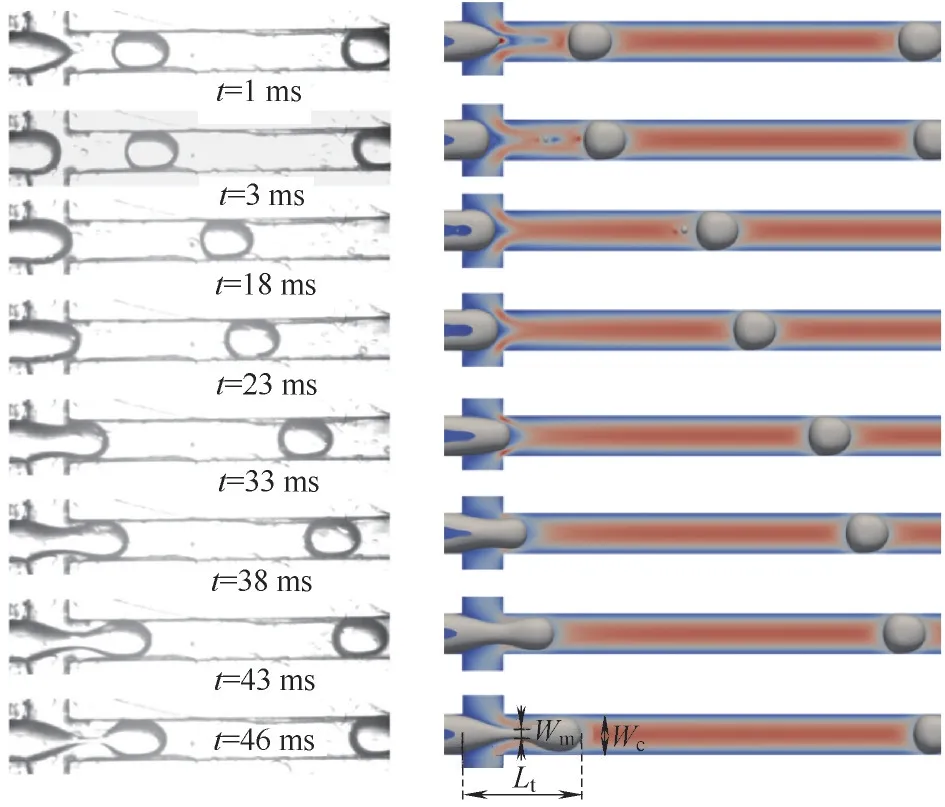
圖3 液滴脫離過程中形態變化對比Fig.3 Comparison between calculated results and experimental data

液滴形成過程中兩相不混溶線總長度Lt和頸部寬度Wm隨時間的變化如圖4 所示，在液滴生成過程的初始階段Lt增長緩慢，隨著時間的推移增長速度逐漸加快。總長度Lt的偏差主要受壁面潤濕特性的影響，由于文獻未給出壁面接觸角，本文假設壁面被連續相完全潤濕，造成破裂過程中總長度略小于實驗測量值，壁面潤濕特性對頸部寬度基本不會產生影響，因此模擬獲得的頸部寬度數據與實驗吻合較好。

3.1.2 冪律流體模型驗證 為驗證冪律流體模型的準確性，基于Fu 等[24]的實驗條件，模擬了微通道內的冪律剪切致稀流體的單相流動。計算模型為正方形截面的直通道，截面邊長為0.6 mm。流體采用0.1%(質量)的PAAm 水溶液，為典型的冪律剪切致稀流體，實驗測得該流體的K 和n分別為0.35 Pa·sn和0.47。通道中部沿徑向的速度大小如圖5(a)所示，模擬結果與實驗數據一致，說明該模型可以較好預測冪律流體在微通道內的流動狀況。軸向截面的速度分布如圖5(b)所示，流動主要集中在通道中央，壁面附近流速較小，由于邊界層的存在，使壁面附近形成較大的速度梯度（剪切率），而在主流區速度梯度基本為0。由于該流體剪切致稀的性質會形成圖5(c)所示的黏度分布，在壁面附近高剪切率區流體黏度較小，而在管道中央剪切率基本為零的區域會形成高流體黏度區。

3.2 液滴生成

3.2.1 液滴生成過程 根據瞬態形態的不同，整個液滴生成過程大致可分為三個階段，如圖6所示。

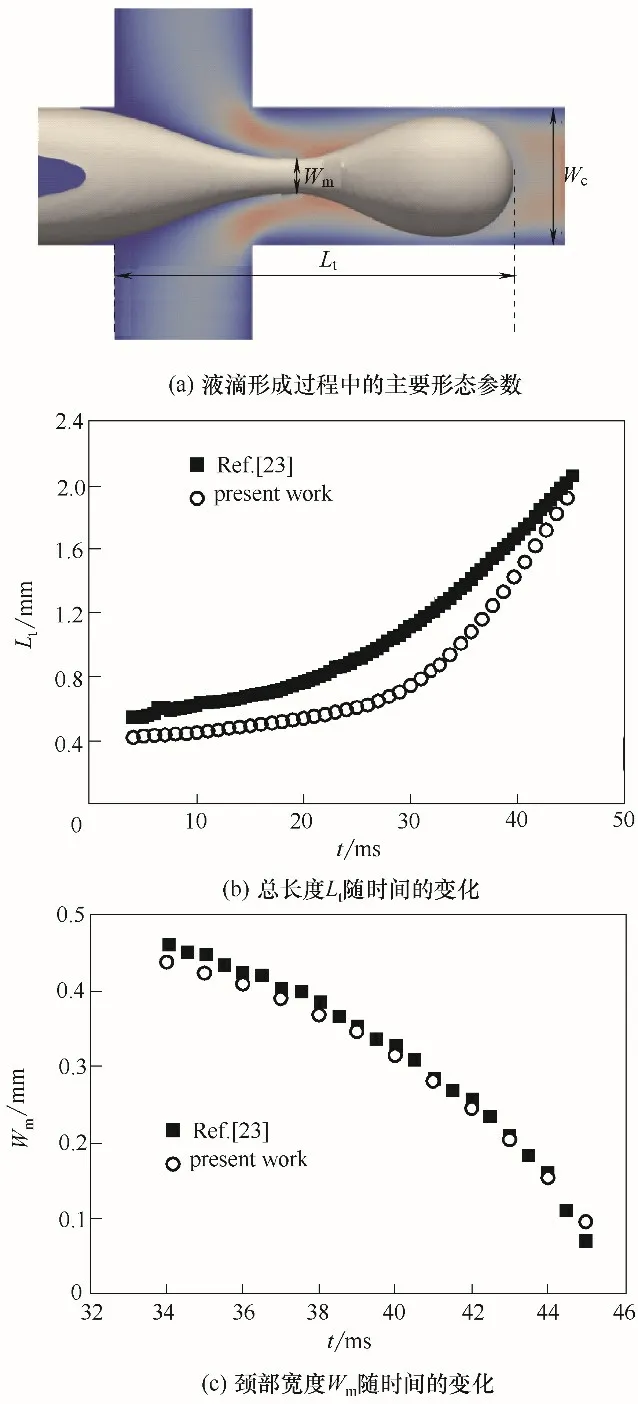
圖4 液滴生成過程中主要形態參數的瞬態變化Fig.4 Temporal evolutions of thread tip and minimum width of thread neck during droplet formation process

（1）離散相流體在交叉口處成泡，并生長至頸部開始出現。由于界面張力的限制作用，該階段的持續時間較長，約持續120 ms，占整個液滴生成周期的大部分。離散相在黏性剪切力的作用下會在界面附近形成兩個軸對稱的渦，促使液泡在交叉處繼續膨脹。

（2）頸部快速收縮直至液滴發生斷裂。此過程持續時間較短，從120 ms 開始約持續28 ms。該階段內相界面處渦流現象消失，離散相頭部達到與連續相相同的流速，但頸部會出現明顯的速度梯度。其主要原因是當頸部出現后，頸部處的界面張力由限制作用轉變為推動作用，結合流動壓力和黏性剪切力促使液滴迅速生長脫離。

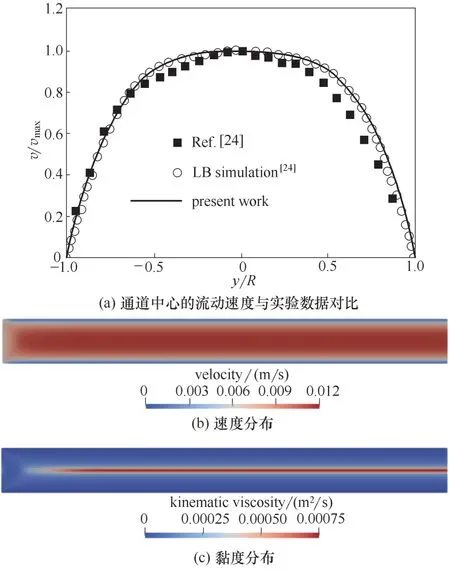
圖5 微通道內速度及黏度分布狀況Fig.5 Velocity and viscosity distribution in microchannel

（3）液滴斷裂瞬間至第二個液泡開始生長，該過程持續時間極短，只有1 ms 左右。在界面張力的作用下，生成的液滴尾部和離散相前緣迅速收縮成半球狀，達到平衡狀態，此過程兩相界面處仍保持較大速度，而后由于界面張力的阻礙作用，液泡內速度分布逐漸減小達到0 ms 時刻的狀態，新的液滴在此基礎上繼續生成。

由于連續相壓力、黏性剪切力和界面張力在液滴形成過程中作用程度的不同，會使液滴的破碎呈現擠壓狀、滴狀和射流狀三種不同的流型。在擠壓狀流型中，離散相會在膨脹階段完全堵塞交叉結構，此時液滴破裂主要由連續相壓力控制，受兩相流率的影響較大。隨著連續相流率或黏度的增大，作用在界面上的黏性剪切力增大，液滴破碎模式開始由擠壓狀向滴狀轉變。滴狀破碎過程與擠壓狀類似，主要區別是，在滴狀流型中液滴不會完全堵塞交叉口，液滴與壁面之間始終存在一層連續相液膜。因此，上游連續相壓力的效果減小，液滴生成主要由黏性剪切力和界面張力控制，主要受連續相毛細數的影響。隨著黏性剪切力的進一步增大，液滴破碎開始進入射流狀流型，此時液滴破裂發生在交叉口下游，連續相壓力在破碎過程中基本不起作用，離散相在黏性剪切力的作用下頭部失穩并斷裂成單分散液滴。

圖6 液滴形成過程中速度分布（Qd=60 μl/min，Qc=480 μl/min，K=0.35 Pa·sn，n=0.47）Fig.6 Velocity distribution during droplet formation process

3.2.2 冪律指數的影響 模擬研究了冪律指數n對液滴生成過程、尺寸及頻率的影響。微液滴生成過程中液泡長度Lt及頸部寬度Wm的變化如圖7所示。圖7(a)表明離散線在初始階段受限于界面張力的作用生長緩慢，隨時間保持近似線性關系。隨著時間的發展，當頸部出現之后離散線開始迅速生長并斷裂，長度呈現近似指數增長的趨勢。此外，隨著n 的增大，液泡演變周期T 逐漸減小。圖7(b) 為頸部寬度的演變過程，表明頸部寬度Wm與周期內剩余時間T－t 呈冪律關系，其變化規律可表示為

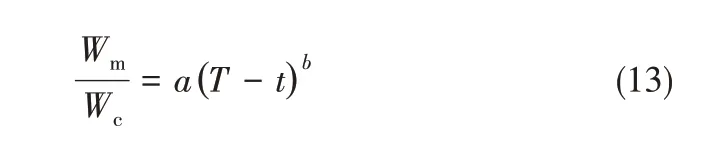
式中，a 和b 均為經驗系數，與Fu 等[23]提出的微液滴在牛頓流體中生成時的頸部寬度變化規律一致。

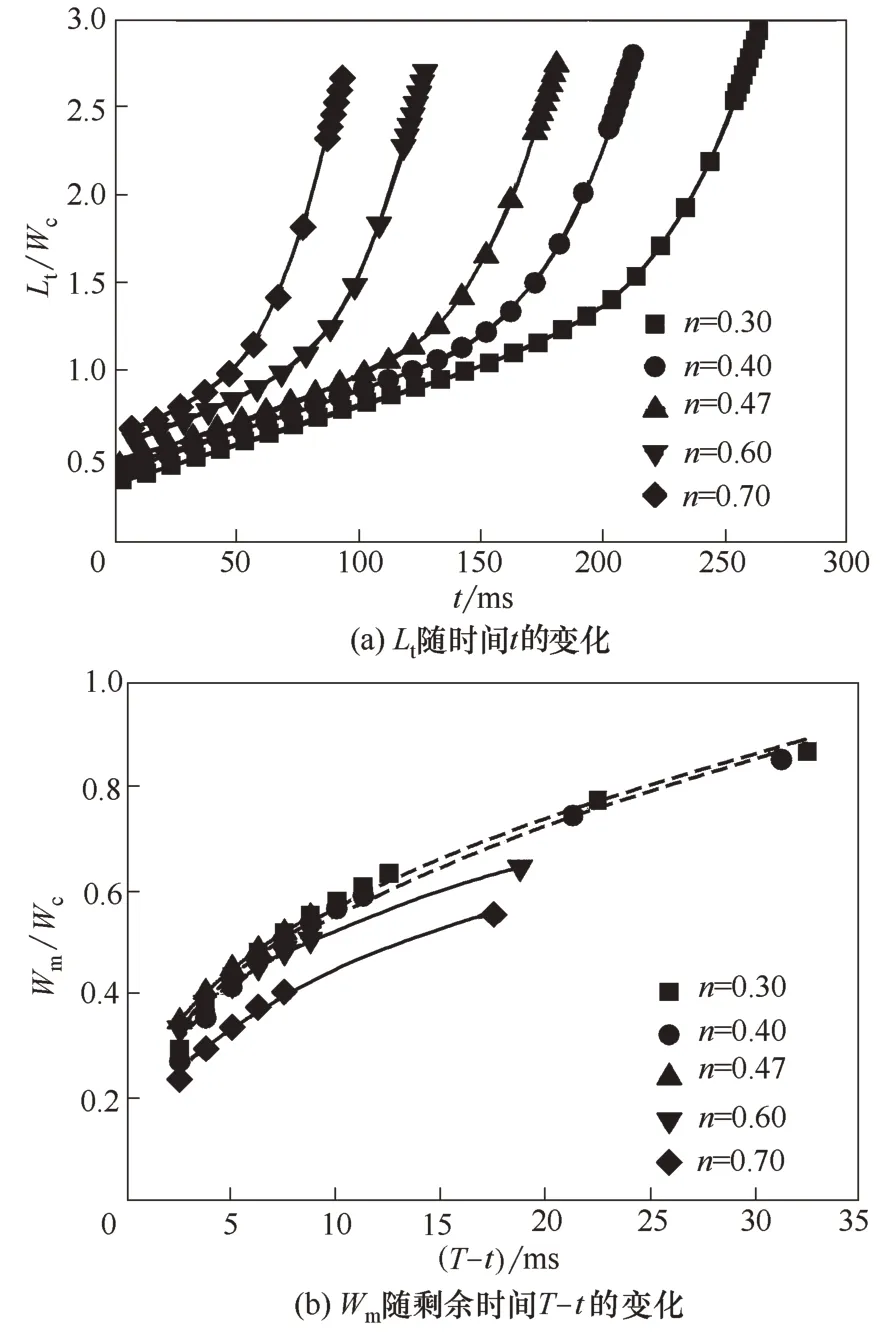
圖7 不同n下不混溶線形態的變化過程（Qd=60 μl/min，Qc=480 μl/min，K=0.35 Pa·sn）Fig.7 Break-up dynamics of dispersed thread for various n

不同n的剪切致稀流體中微液滴的生成過程如圖8所示，在其他條件不變的情況下，液滴的生成周期及大小均隨著n 的增加而減小。主要原因是，連續相流體的有效黏度（μeff）隨著n 的增加而增加，使作用在界面上的黏性剪切力更容易克服界面張力的限制，從而使液滴尺寸和生成時間減小。毛細數Ca 作為衡量黏性力與界面張力的無量綱數，表達式為

由于流動過程中非牛頓流體的黏度不穩定且不均勻，通過傳統的計算方法無法得到Ca 的數值。因此，本文通過引入一個計算平均剪切率的方法來實現冪律流體Ca的計算[25]

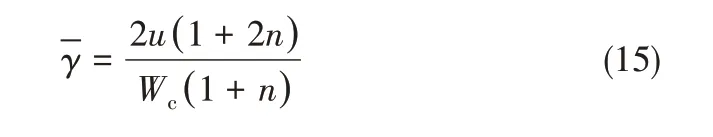
隨著連續相Ca的增大，通道內的兩相流型由擠壓狀轉變為滴狀，最終轉化為射流狀，與現有的研究一致。

圖9(a)表明由于連續相有效黏度的增大，液滴的無量綱長度隨n 的增大而減小。Sontti 等[14]和Shi等[15]模擬了T 型通道內牛頓微液滴在不同冪律流體中的生成過程，液滴大小隨n的變化趨勢相似，且都呈現線性變化。圖9(b)表示液滴生成頻率f 隨n 的變化，隨著n的增大液滴生成頻率逐漸增大。

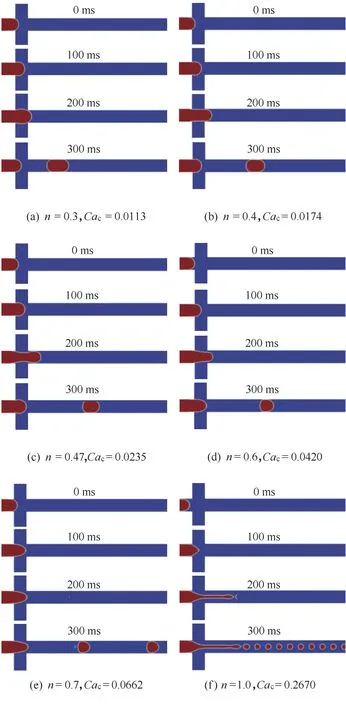
圖8 不同n冪律流體中牛頓液滴的形成機制（Qd=60 μl/min，Qc=480 μl/min，K=0.35 Pa·sn）Fig.8 Newtonian droplet formation mechanism in power-law fluids with different n

3.2.3 稠度系數的影響 本文還研究了稠度系數K對液滴生成的影響。式(6)表明隨著K 的增大，連續相流體黏度等比增大。Lt和Wm的變化如圖10所示，相比n 的變化，K 的變化對生成周期的影響相對較小，且隨著K 的增大，差距逐漸減小。圖10(b)表明頸部寬度仍與(T－t)b呈正比，且當K和n改變時，b的變化范圍不大。圖11 為不同K 條件下單個液滴生成的演化過程，隨著K的增大，液滴的大小和生成周期逐漸減小，液滴生成呈現更快更小的趨勢。此外，隨著K的進一步增大，流型也將由滴狀向射流狀轉變。

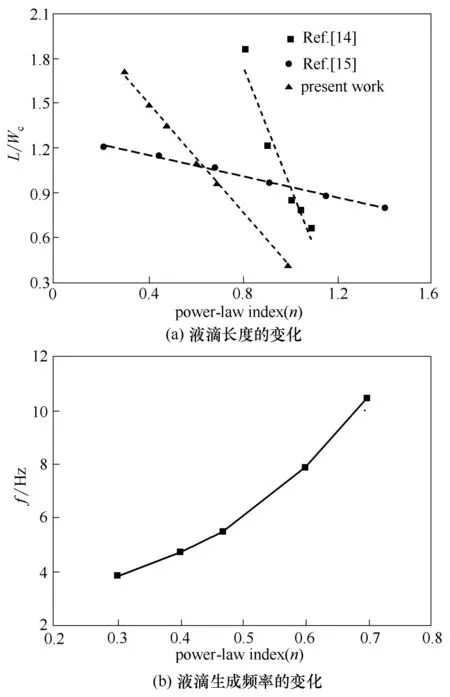
圖9 液滴尺寸及生成頻率隨n的變化（Qd=60 μl/min，Qc=480 μl/min，K=0.35 Pa·sn）Fig.9 Variations of droplet size and formation frequency with n

微通道內的液滴生成過程可以看作一個半穩定過程，當離散相流率不變時單個液滴的體積V 與生成頻率f的關系可以表示為

由于連續相黏度的增大，液滴尺寸隨著K 的增大而減小，因此生成頻率呈現逐漸增大的趨勢，如圖12所示。

液滴無量綱長度隨連續相毛細數Cac的變化如圖13 所示，液滴的長度與Cac呈現冪指數關系，與Fu等[26]的實驗研究結果一致，將Shi等[15]的模擬數據按照該方式擬合可以得到同樣的規律，該規律可用于液滴生成大小的簡單預測。

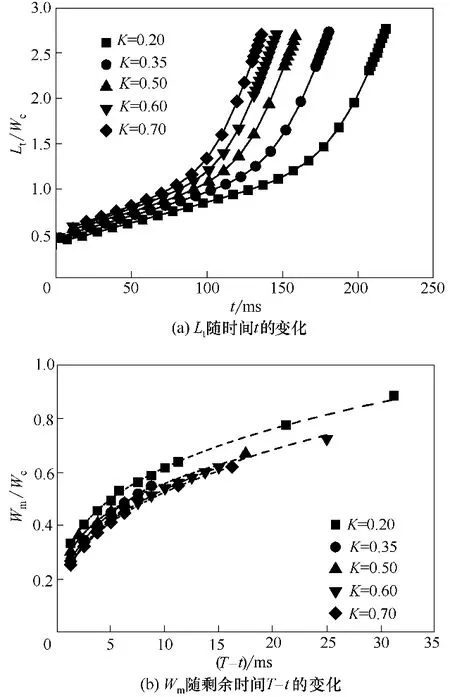
圖10 不同K下不混溶線形態的變化過程（Qd=60 μl/min，Qc=480 μl/min，n=0.47）Fig.10 Break-up dynamics of dispersed thread for various K

4 結 論

本研究基于開源CFD 平臺OpenFOAM，對流動聚焦微通道內非牛頓流體作為連續相的微液滴生成進行了數值模擬。首先，通過與實驗數據對比驗證了數值方法的可行性和準確性。然后，基于此驗證，模擬了流動聚焦微通道內微液滴在冪律剪切致稀流體中的形成機理及行為，研究了稠度系數和冪律指數的影響。

通過與文獻中的實驗數據進行對比表明，interFoam 求解器對液滴在微通道內的生成和流動狀況可以做出較好預測，證明該求解器可以用于模擬該尺度下微通道內的兩相流動，且計算精度滿足要求。此外，通過與非牛頓流體流動速度分布的實驗數據對比，驗證了冪律剪切致稀非牛頓流體模型用于計算微通道內非牛頓流體流動時的準確性。

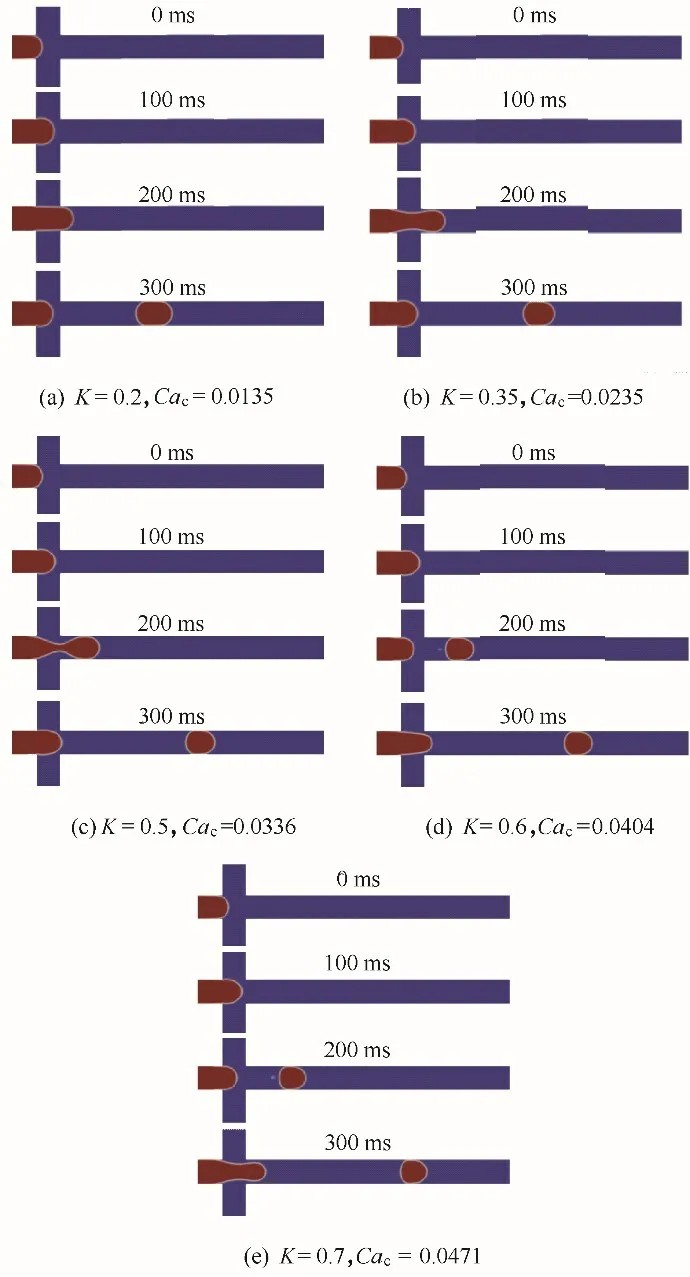
圖11 不同K冪律流體中牛頓液滴的形成機制（Qd=60 μl/min，Qc=480 μl/min，n=0.47）Fig.11 Newtonian droplet formation mechanism in power-law fluids with different K

通過對冪律流體中微液滴生成過程的模擬研究表明，在液滴生成過程的初期，離散相頸部緩慢縮小；但后期在連續相壓力和界面張力的共同作用下，液泡頸部迅速縮小并斷裂。頸部寬度Wm與周期剩余時間(T－t)呈冪律關系。此外，在液滴生成的初期，液泡總長度Lt隨時間緩慢增長，并與時間呈線性關系；在后期，由于界面張力方向的改變，液泡的總長度以類似指數函數的形式隨時間迅速增長。

通過分別改變冪律連續相流體的K 和n，研究了它們對微液滴的尺寸和生成周期的影響。結果表明，液滴的尺寸隨K 或n 的增大而減小，生成頻率則隨著兩個值的增大而增大。相對于K 的變化，n的變化對液滴尺寸和生成周期的影響更加顯著。隨著K 和n 的增大，兩相流型均呈現由擠壓狀向滴狀進而向射流狀的轉變。此外，研究表明改變連續相的流變特性，液滴的長度與連續相毛細數呈冪律關系。

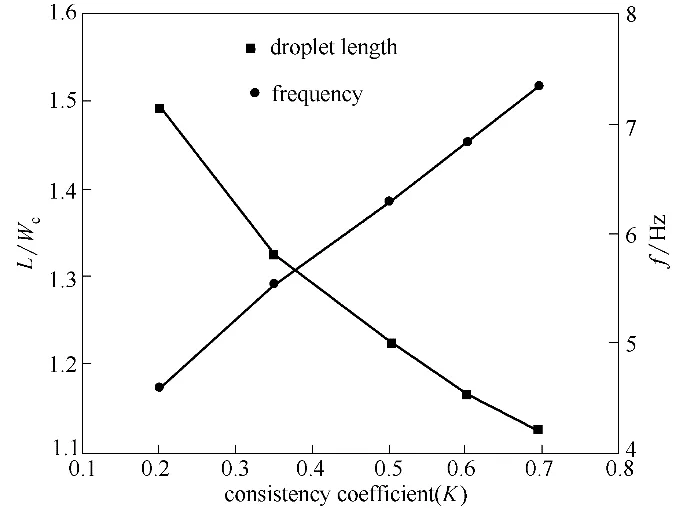
圖12 液滴長度及生成頻率隨K的變化（Qd=60 μl/min，Qc=480 μl/min，n=0.47）Fig.12 Variations of droplet size and formation frequency with K

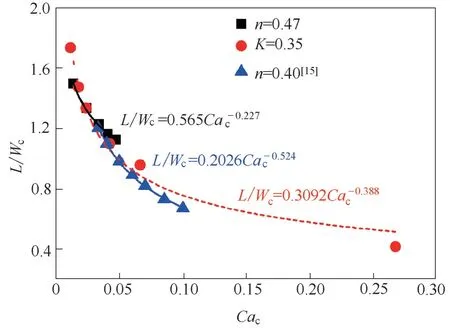
圖13 液滴長度與連續相毛細數的關系Fig.13 Relationship between droplet length and capillary number of continuous phase

符 號 說 明

c——界面壓縮模型中的可控壓縮因子

dh——微通道水力直徑，μm

Fs——體積表面張力，N/m3

f——液滴生成頻率，Hz

g——重力加速度，m/s2

K——冪律非牛頓流體稠度系數，Pa·sn

L——生成液滴的長度，μm

Le——微通道入口段長度，μm

Lt——兩相不混溶線總長度，μm

Mw——壁面附近界面的單位切向量

N——壁面附近網格單元的界面法向量

Nw——壁面附近界面的單位法向量

n——冪律非牛頓流體冪律指數

p——壓力，Pa

Qc，Qd——分別為連續相和離散相入口流率，μl/min

Re——Reynolds數

T——單個液滴生成周期，ms

t——時間，ms

u——通道內流動速度大小，m/s

u——速度矢量，m/s

uc——界面壓縮模型中需要模化的速度，m/s

V——單個液滴體積，μl

Wc——通道寬度，μm

Wm——不混溶離散相的頸部寬度，μm

α——相分數

γ——剪切率，s-1

-γ——剪切致稀非牛頓流體平均剪切率，s-1

θw——壁面處的靜態接觸角，(°)

κN——界面曲率

μ——動力黏度，Pa·s

μeff——非牛頓流體的有效黏度，Pa·s

ρ——流體密度，kg/m3

σ——界面張力系數，N/m

τ——剪切應力，N/m2

下角標

c——連續相

d——離散相