基于變異粒子群算法的局部陰影光伏陣列MPPT 研究

沈 攀，付 波

（湖北工業大學太陽能高效利用及儲能運行控制湖北省重點實驗室 電氣與電子工程學院，湖北 武漢 430068）

0 引言

隨著化石能源的日漸枯竭，太陽能作為一種清潔可再生能源越來越受到廣泛關注。在局部陰影情況下，光伏陣列的P-U特性曲線有多個極值點，此時傳統的MPPT 算法就會失效[1]。

針對這個問題，國內外許多學者做了大量的研究。文獻[2-4]利用神經網絡來進行MPPT 控制，神經網絡具有很強的學習能力，經過一定的學習之后，可以直接根據環境參數預測出光伏陣列的最佳工作電壓。文獻[5-6]利用粒子群算法來進行最大功率點跟蹤，避免了算法陷入局部極值尋優。

考慮到多極值光伏陣列的復雜性，本文提出一種基于變異粒子群算法的MPPT 控制策略，通過引入變異機制來增強算法的全局尋優能力，避免算法陷入局部極值。與傳統的MPPT 算法相比，本方法跟蹤精度更高，過程更平穩，提高了局部陰影情況下光伏陣列的能量利用效率。

1 光伏電池模型及輸出特性

1.1 光伏電池數學模型

為研究光伏電池的輸出特性，通常將光伏電池用一個由電流源、二極管、并聯電阻、串聯電阻組成等效電路來模擬，如圖1 所示。

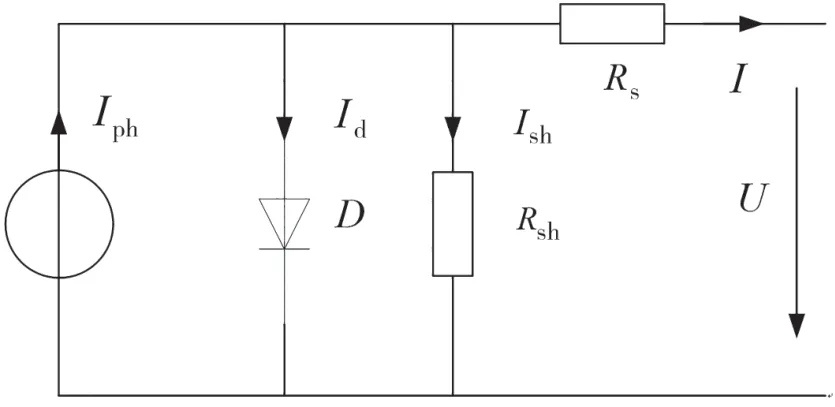
圖1 光伏電池等效電路

其中，Iph表示電流源電流，D 為反并聯二極管，Rs和Rph分別表示光伏電池的串聯電阻和并聯電阻。光伏電池輸出電流的數學方程為：

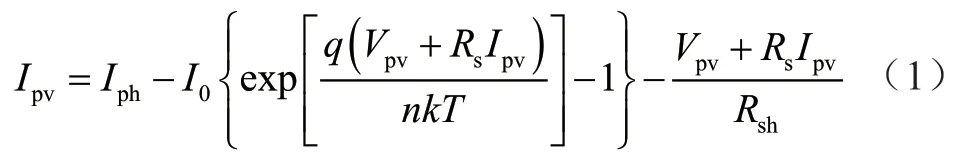
其中，I0為二極管反向飽和電流，Iph為光伏感應電流，k為玻爾茲曼常數，n為二極管理想因子，T為光伏電池溫度，q為電子荷電常數。

1.2 陰影情況下光伏陣列輸出特性

由于單塊光伏電池輸出功率較小，為滿足需要通常將光伏電池通過串聯以及并聯構成光伏陣列。當光伏陣列所受光照強度均勻時，光伏陣列的P-U特性曲線為只有一個極值的單峰曲線。當處于陰影情況時，光伏陣列所受光照不均勻，此時光伏陣列的P-U特性曲線呈現出多個極值點，其中只有一個極值點為全局最大功率點，其余極值點為局部極值點。

圖2 表示的是一個由3 塊光伏電池串聯組成的光伏陣列在不同光照情況下的P-U特性曲線。無陰影情況下，光伏陣列所受光照強度均為1 000 W/m2，局部陰影情況PSC1：光照強度依次為[1000、600、200]W/m2，局部陰影情況PSC2：光照強度依次為[1000、500、500]W/m2。

圖2 不同光照情況光伏陣列P-U 特性曲線

2 光伏陣列MPPT 算法

2.1 擾動觀測法

擾動觀測法是一種傳統的MPPT 算法，具有原理簡單、易于實現等優點，其基本流程如下。

步驟一，測量光伏陣列當前時刻的工作電壓U0和輸出功率P0。

步驟二，對當前工作電壓施加一個擾動量ΔU，使其工作在Ut，輸出功率為Pt。

步驟三，判斷擾動后的輸出功率Pt與擾動前的輸出功率P0的大小。

步驟四，若Pt大于P0，則繼續往相同方向施加擾動，否則往反方向施加擾動。

雖然擾動觀測法簡單易實現，但其最大功率點跟蹤性能受步長影響很大。當步長較大時，光伏系統輸出功率會產生很大的波動。當步長較小時，算法跟蹤速度慢且容易陷入局部極值點，不能準確跟蹤到全局最大功率點。

2.2 粒子群算法

粒子群算法（PSO）是一種經典的智能優化算法，它能通過粒子的不斷迭代實現全局尋優。PSO 中的粒子具有位置和速度兩個屬性，在迭代的過程中，粒子的位置由當前粒子的歷史最優位置Pi和種群的歷史最優位置Pg實現更新。第t+1 次迭代時，粒子i的速度和位置根據如下公式更新：

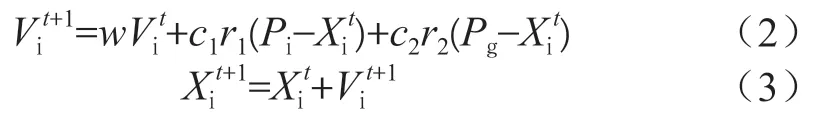
其中，w為慣性權重，c1、c2為學習因子，r1、r2為（0，1）的隨機數。

2.3 變異粒子群算法

本文將變異機制引入粒子群算法中，提出一種變異粒子群算法。當粒子按式（3）更新其位置后，對更新后的位置進行變異，若粒子變異后的位置優于，則粒子位置更新為變異后的位置，否則不變異。粒子位置按式（4）進行變異：

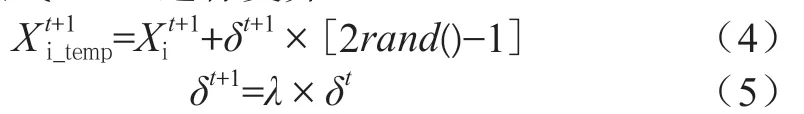
本文通過對粒子群算法進行變異，顯著增強其跟蹤全局最大功率點的能力，提高了算法的全局尋優性能。變異粒子群算法的流程如圖3 所示。

圖3 變異粒子群算法流程圖

3 仿真及結果分析

為驗證本文所提變異粒子群算法的有效性，在理論分析的基礎上進行Matlab/Simulink 仿真，光伏MPPT系統基于Boost 電路，如圖4 所示。Boost 電路的主要參數為：C1=10 μF，濾波電感L=1 mH，母線電容C2=100 μF，負載電阻R=20 Ω，開關頻率fs=10 kHz。

光伏陣列采用3 塊光伏組件串聯而成，在光照強度為局部陰影PSC1 時，光伏陣列的P-U特性曲線呈現出三個極值點的情況，如圖2 所示。其中，全局最大功率點為：388.5 W，其余兩個局部極值點分別為263 W 和221.6 W。在局部陰影PSC1 下，對基于Boost電路的光伏MPPT 系統分別采用變異粒子群算法和擾動觀測法進行仿真對比，算法中粒子數目為6，粒子初始位置在解空間中均勻分布，初始變異步長為1/2 的解空間長度，其結果如圖5、圖6 所示。

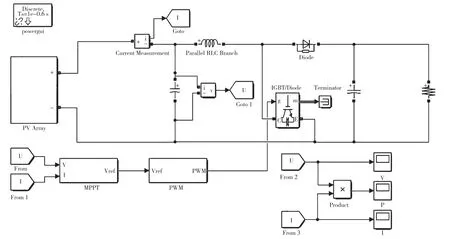
圖4 基于Boost 電路的光伏MPPT 系統

圖6 局部陰影PSC1 情況下擾動觀測法功率跟蹤曲線

由仿真結果可以看出，變異粒子群算法在1.1 s 時準確地跟蹤到了全局最大功率點388.3 W，功率輸出波動較小，與最大功率點真實值388.5 W 相比，相對誤差為0.05%。擾動觀測法控制下，在0.21 s 時跟蹤到的功率為262.8 W 并且存在較大的波動，對比圖2 可知擾動觀測法陷入了第一個局部極值點。與擾動觀測法相比，本文提出的變異粒子群算法在光伏陣列局部陰影情況下輸出功率波動小，跟蹤精度更高。

4 結論

局部陰影情況下，傳統的MPPT 算法不能準確地跟蹤到全局最大功率點。為了減小能量損失，本文在粒子群算法的基礎上引入變異機制，提出一種變異粒子群算法并用于光伏陣列的MPPT 控制。通過仿真分析可以得出如下結論。

（1）本文提出的算法在局部陰影情況下具有良好的全局尋優性能，并且跟蹤過程更加穩定，功率波動更小。

（2）局部陰影情況下，傳統的MPPT 算法不能準確地跟蹤到全局最大功率點，本文提出的算法比傳統的MPPT 算法具有更好的控制效果。