理想狀態(tài)下的同心鼓策略研究

劉曉扣 管仁永 姜國柱

摘 要：文章研究的是在理想狀態(tài)下同心鼓的協(xié)作最優(yōu)策略。假設(shè)平衡狀態(tài)后的排球與鼓的碰撞點(diǎn)為定點(diǎn)，考慮空氣阻力的影響以及人數(shù)的不確定性，研究平衡狀態(tài)后的運(yùn)動(dòng)過程，文章由動(dòng)量守恒和動(dòng)能守恒建立微分方程，由目標(biāo)規(guī)劃得到了策略模型，最后進(jìn)行求解，得到最佳策略。

關(guān)鍵詞：微分方程;彈性碰撞;目標(biāo)規(guī)劃

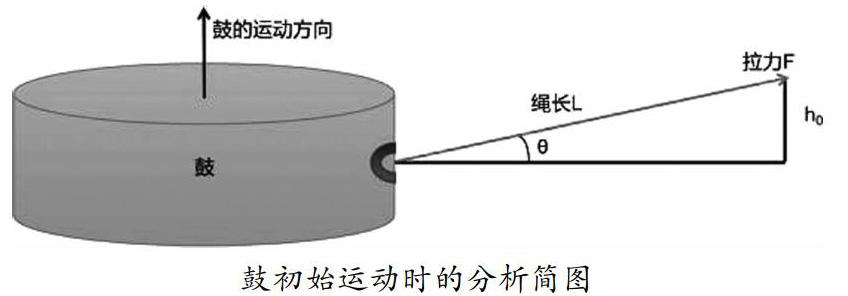
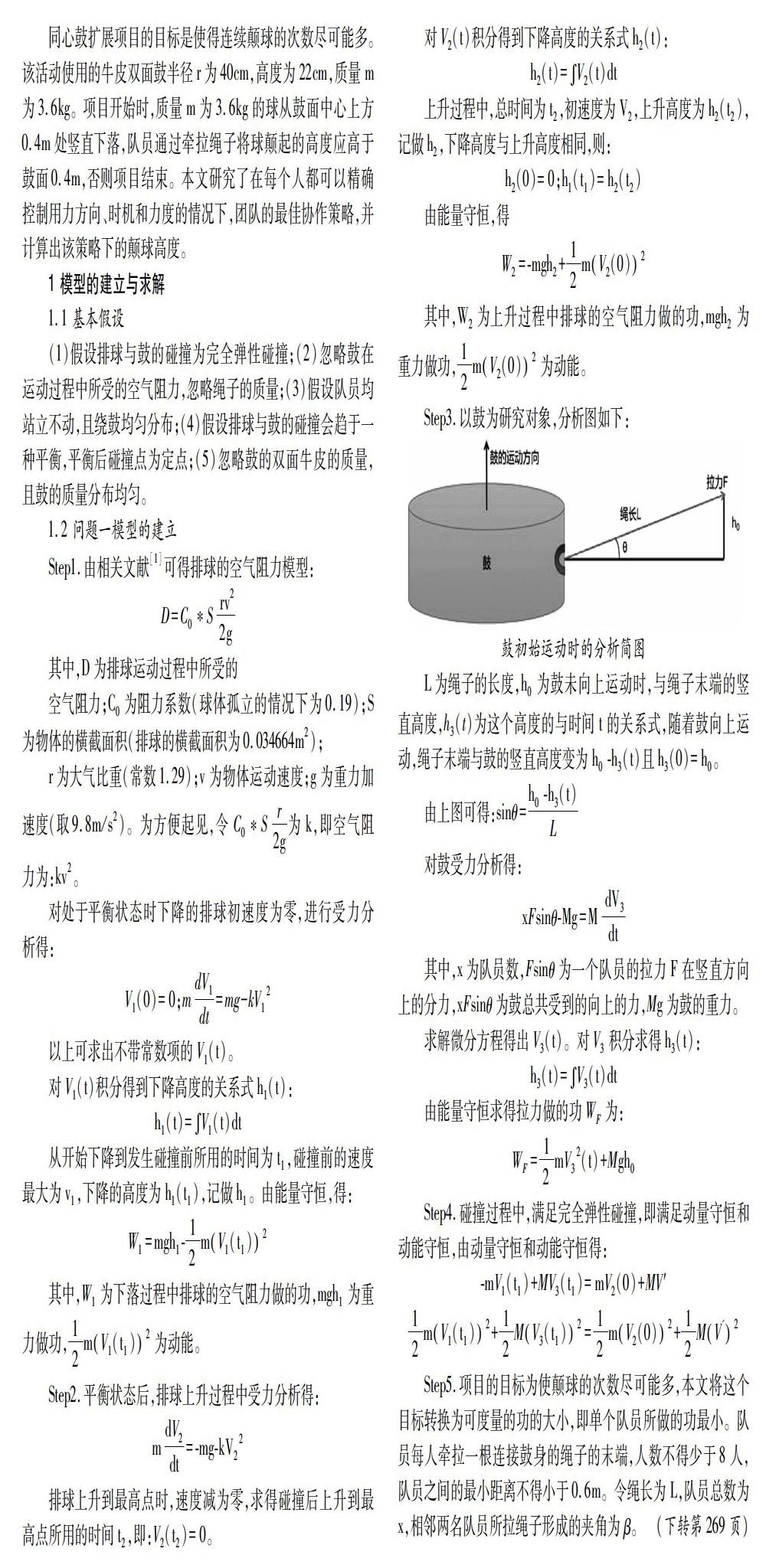
同心鼓擴(kuò)展項(xiàng)目的目標(biāo)是使得連續(xù)顛球的次數(shù)盡可能多。該活動(dòng)使用的牛皮雙面鼓半徑r為40cm，高度為22cm，質(zhì)量m為3.6kg。項(xiàng)目開始時(shí)，質(zhì)量m為3.6kg的球從鼓面中心上方0.4m處豎直下落，隊(duì)員通過牽拉繩子將球顛起的高度應(yīng)高于鼓面0.4m，否則項(xiàng)目結(jié)束。本文研究了在每個(gè)人都可以精確控制用力方向、時(shí)機(jī)和力度的情況下，團(tuán)隊(duì)的最佳協(xié)作策略，并計(jì)算出該策略下的顛球高度。

1 模型的建立與求解

1.1 基本假設(shè)

（1）假設(shè)排球與鼓的碰撞為完全彈性碰撞;（2）忽略鼓在運(yùn)動(dòng)過程中所受的空氣阻力，忽略繩子的質(zhì)量;（3）假設(shè)隊(duì)員均站立不動(dòng)，且繞鼓均勻分布;（4）假設(shè)排球與鼓的碰撞會(huì)趨于一種平衡，平衡后碰撞點(diǎn)為定點(diǎn);（5）忽略鼓的雙面牛皮的質(zhì)量，且鼓的質(zhì)量分布均勻。

1.2 問題一模型的建立

Step1.由相關(guān)文獻(xiàn)[1]可得排球的空氣阻力模型：

1.3 模型的求解

（1）由于碰撞不會(huì)第一次就達(dá)到平衡狀態(tài)，因此讓隊(duì)員們第一次的發(fā)力略大于平衡狀態(tài)時(shí)的用力，使排球與鼓第一次碰撞之后，就達(dá)到平衡狀態(tài)。

（2）從最優(yōu)策略出發(fā)，當(dāng)上升高度正好為0.4m的時(shí)候，每個(gè)人的用力達(dá)到最小。當(dāng)每個(gè)人的距離正好為0.6m時(shí)，繩子的長(zhǎng)度達(dá)到最短，所用的繩子最少。人工求解目標(biāo)二元函數(shù)的極值點(diǎn)，該極值點(diǎn)為最優(yōu)解：人數(shù)20人，每個(gè)人的用力大小為51N，繩長(zhǎng)為1.72m，初始位置較繩子水平時(shí)的高度為0.2559m。

2 結(jié)語

本文對(duì)運(yùn)動(dòng)過程進(jìn)行了適當(dāng)簡(jiǎn)化，分析了在理想情況下，即每個(gè)人都可以精準(zhǔn)控制用力時(shí)，同心鼓項(xiàng)目的最優(yōu)協(xié)作策略，本文所建立的模型，為同心鼓相關(guān)研究提供了依據(jù)，對(duì)該項(xiàng)活動(dòng)的開展具有一定的指導(dǎo)意義。

參考文獻(xiàn)：

[1]顧偉農(nóng)，焦峪平.空氣阻力對(duì)排球正面上手發(fā)球水平方向飛行距離的影響實(shí)驗(yàn)分析[J].兵團(tuán)教育學(xué)院學(xué)報(bào)，2002（3）.

作者簡(jiǎn)介：劉曉扣（1998-），女，漢族，山東濟(jì)寧人，本科，學(xué)生，研究方向?yàn)槲锪鞴芾怼?/p>