多元線性分析在儲糧真菌生長預測中應用研究

王鵬杰 祁智慧 張海洋 田 琳 高瑀瓏 唐 芳

(國家糧食和物資儲備局科學研究院1，北京 100037)

(南京財經大學2，南京 210023)

稻谷儲藏期間，霉變是造成儲糧損失的一個重要因素。近幾十年來，國內外有關稻谷儲藏霉變的研究報道很多。Laca等[1]研究發現霉菌主要分布在稻谷表面。Genkawa等[2]研究了不同水分的稻谷儲藏過程中霉菌數量的變化，低水分稻谷無霉菌生長，其儲藏的效果同低溫儲藏一樣有效。周建新等[3-5]研究了不同貯藏條件下稻谷真菌的變化情況，環境溫度和稻谷含水量對稻谷儲糧真菌生長有直接影響，儲藏溫度和時間與霉菌量呈顯著的二元線性關系。金昌福[6]等利用近紅外檢測技術，建立了貯藏環境溫度和水分含量對貯藏稻谷表面霉菌菌落總數影響規律的多元線性回歸模型。唐芳等[7]通過對稻谷儲藏過程中水分和溫度的變化與真菌生長關系的研究，得出稻谷儲存水分、溫度與真菌起始生長時間的關系曲線。上述研究都是側重于一個或兩個因素的影響，而真菌生長是受多個因素的影響，且相互耦合共同對真菌生長產生影響，因此，要更真實地反映真菌生長狀況，需基于大量數據進行統計分析，建立多影響因素的真菌生長預測模型。

多元線性回歸是多元統計分析中一種重要方法，可以解決多個因素對同一變量影響的相關性分析，進而建立相關性的統計模型。Green等[8]基于室內溫度、濕度等變量建立了室內有害微生物的多元線性回歸預測模型，預測模型精度可達97%。南英華等[9]建立了泉流量與大氣降水的多元線性回歸模型。本文基于水分、溫度和儲藏時間三個主要影響因素，定期采集真菌生長數據，采用多元線性回歸建立儲糧真菌生長預測模型，并對模型進行了F檢驗、t檢驗和殘差分析，結合稻谷實倉數據對預測模型進行了初步驗證。

1 材料與方法

1.1 模擬儲藏實驗材料及樣品處理

取自黑龍江的粳稻樣品，采用噴霧加無菌水方式，將樣品水分含量調至目標水分，密封于4 ℃低溫均衡水分。目標水分含量較高的樣品，需多次加水，低溫均衡水分時間至少30 d，直至稻谷含水量含量達到目標水分并通過水分均勻性檢驗。

1.2 試劑和儀器

HPS-250生化培養箱；PL3002-IC電子分析天平；SMART顯微鏡。

1.3 實驗方法

1.3.1 模擬儲藏及檢測周期

將不同水分含量(13.0%、13.5%、14.0%、14.5%、15.0%、15.5%、16.0%、16.5%、17.0%、17.9% )的稻谷樣品，密封并分別置于不同溫度的(10、15、20、25、30、35 ℃)生化培養箱中模擬儲藏180 d，每10 d取樣一次，檢測儲糧真菌生長數量。

1.3.2 稻谷實倉情況及取樣方法

選擇華北地區某糧庫稻谷倉為實驗倉。稻谷倉基本信息：2017年1月入庫，產地黑龍江，容量6 000 t，入倉水分為14.5%。取樣位置的選擇與糧情檢溫電纜表層布點位置相重合，具體分布如圖1所示。取樣深度為距離糧面0.4 m深度。度夏期間采用手動扦樣器定期取樣，每次取樣200 g，置于無菌袋中保存，取回后4 ℃低溫保存，以備檢測。

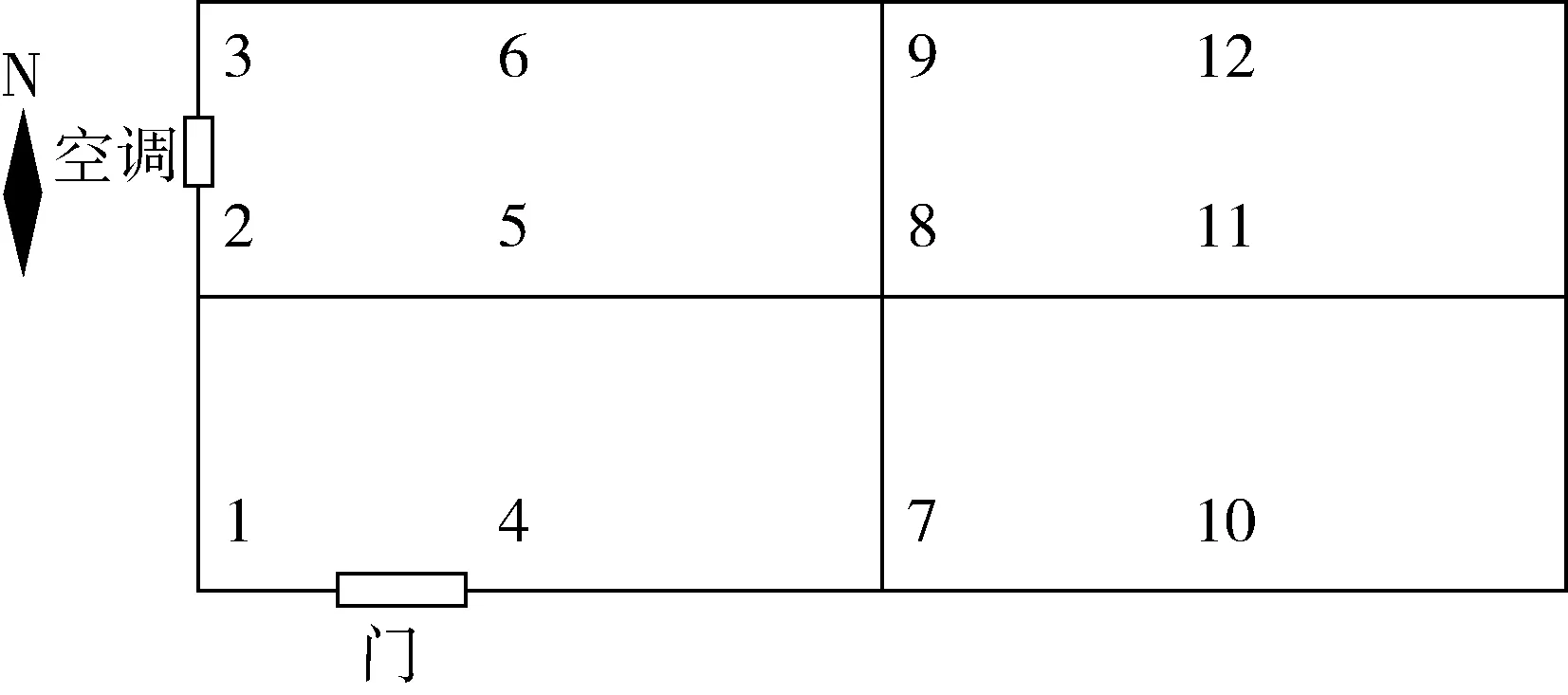
圖1 實驗倉扦樣點位置示意圖

1.3.3 儲糧真菌檢測方法

參照LS/T 6132《糧食檢驗 儲糧真菌的檢測 孢子計數法》。

1.3.4 稻谷含水量測定方法

參照GB/T 5497 糧食、油料檢驗水分測定法 105 ℃烘干法。

1.3.5 糧溫檢測方法

參照糧庫內糧情檢測系統表層糧溫數據。

1.4 數據處理方法

1.4.1 真菌生長數據預處理方法

本實驗設置了10個水分梯度的稻谷樣品，6個模擬儲藏溫度，180 d中，對每個梯度的樣品每10 d取一次樣，檢測儲糧真菌生長數量，共取19次，總計1 140組數據，每次取樣做雙實驗，兩次結果偏差超過50%時，重新取樣檢測，檢測結果取平均值。

真菌孢子數在103～107個/g范圍，且微生物生長為非線性，根據微生物生長模型處理經驗[10]，對真菌孢子數進行對數變換，不僅利于線性回歸，而且可以縮小數據的絕對值以方便數據處理，降低樣本的異方差程度[11]。真菌檢測方法的檢出限為3×104個/g，對于未檢出真菌生長的樣品，并不代表糧食不攜帶真菌孢子，而是孢子濃度未達到該方法檢出限，依據環境及正常糧食真菌帶菌量經驗數據[12]，將該方法未檢出的稻谷樣品帶菌量補為1×103個/g，更符合稻谷帶菌量的實際情況。

1.4.2 數據分析軟件

文中數據結果由MATLAB2016軟件處理獲得。

2 結果與討論

糧食儲糧真菌的生長受多個因素的影響。多元線性回歸模型，可以實現多個自變量的最優組合共同來預測或估計因變量。其主要步驟如下：第一步，確定自變量和因變量；第二步，根據研究現象，依據相應的理論和經驗，設定模型并加以確定；第三步，參數估計；第四步，模型的檢驗和修正，常用的檢驗有擬合優度檢驗、線性回歸模型F檢驗、參數的t檢驗以及殘差分析。第五步，模型的運用[13]。下面重點介紹建模、模型檢驗及應用。

2.1 多元線性回歸建模

多元線性回歸是一種數理統計方法，設因變量為y，自變量為x，自變量有p個，它們的n組觀測值為(x1i，x2i，xpi，yi)(i=1，2，…，n)，其多元線性回歸表達式如下所示：

β是多元線性回歸方程的系數。

在數據分析過程中，將所得實驗數據導入MATLAB，分別繪制出取對數后的真菌孢子數與環境溫度，稻谷含水量和儲藏時間的散點圖，見圖2。

從圖2中所示的散點圖可看出，取對數后的真菌孢子數分別與環境溫度、稻谷含水量和儲藏時間大致呈線性關系。因此，可以利用MATLAB對其進行多元線性回歸。

本研究對上述實驗采集的1 140組實驗數據，將稻谷儲藏溫度、含水量、儲藏時間作為自變量，取對數處理的真菌孢子數作為因變量，用MATLAB軟件regress語句對這些實驗數據進行擬合，得到的多元線性回歸模型如下：

圖2 取對數后真菌孢子數與環境溫度、儲藏時間及稻谷含水量的散點圖

lny=-20.787+0.157×x1+0.027×x2+1.683×x3

(1)

式中：y表示真菌孢子數，單位為個/g；x1表示環境溫度，單位為℃；x2表示儲藏時間，單位為d；x3表示稻谷含水量，以%表示。

式(1)為以lny為因變量的多元線性方程，對方程(1)進行指數變換，得到以y為因變量的指數函數方程。

y=exp(-20.787+0.157×x1+0.027×x2+1.683 ×x3)

(2)

2.2 預測模型的效果分析

根據實驗數據初步建立了多元線性回歸模型，還須通過模型的擬合優度、方程線性關系的顯著性、系數的顯著性等統計量的檢驗后，才可以用于解釋、分析實際問題[14]。

2.2.1 擬合優度檢驗

擬合度是用于檢驗回歸方程對樣本觀測值的擬合程度。多元線性回歸的擬合程度，使用多重判定系數，其定義為：

式中: SSR為回歸平方和，SSE為殘差平方和，SST為總離差平方和。R2表示因變量與所有自變量之間的線性相關程度，實際反映的是樣本數據與預測數據間的相關程度，R2越接近于1，方程擬合優度越高[15]。R2的平方根稱為復相關系數(R)，本模型的相關系數R= 0.878，判定系數R2= 0.770，這說明取對數后的儲糧真菌孢子數的變化有77%可由環境溫度、稻谷含水量和儲藏時間這三個因素的變動來解釋。

2.2.2 線性關系顯著性檢驗(F檢驗)

在建立多元線性回歸模型之后，還必須對因變量與多個自變量間的線性關系的假設進行顯著性檢驗。F統計量定義為：平均的回歸平方和與平均的殘差平方和之比，對于多元線性回歸方程：

式中: SSR為回歸平方和;SSE為殘差平方和;n為樣本數;k為自變量個數。F統計量服從第一自由度為k、第二自由度為n-k-1的F分布，即F～F(k，n-k-1)。通過查詢F分布分位數表，我們可以得出特定顯著度條件下F檢驗的臨界值。當統計量F的值大于臨界值時，即可認為在總體上自變量與因變量呈顯著的線性關系。F值越大，線性回歸效果越顯著。

在本模型的F檢驗中，總平方和為15 150.32，回歸平方和為11 667.82，殘差平方和為3 482.50。本研究顯著性檢驗的顯著性概率值為0，顯然滿足P<α=0.05。F統計的觀測值為1 219.552，查表得F0.05(3，1 136)= 2.61，F值遠大于F0.05(3，1 136)，表明因變量與自變量之間整體線性關系顯著，即取對數后的真菌孢子數與環境溫度，稻谷含水量和儲藏時間存在顯著多元線性關系。

2.2.3 回歸系數顯著性檢驗(t檢驗)

在多元線性回歸方程中，回歸方程顯著性F檢驗和回歸系數t檢驗是不等價的，還需進行方程回歸系數的t檢驗，以判斷各相關因子之間是否存在共線性現象。統計量t定義為：

給定一個顯著性水平α，可以從t分布分位數表查得tα/2(n-k-1)。當|ti| >tα/2(n-k-1)，P<α=0.05，接受備擇假設H1。本模型各項變量的t顯著性概率均為0，均小于0.05，環境溫度、儲藏時間和稻谷含水量的t統計量分別為24.785、27.175、46.607，均大于t0.025(1 136)= 1.96。由此可見，稻谷含水量、儲藏時間和環境溫度對取對數后的儲糧真菌孢子數均有顯著影響。

2.2.4 殘差分析

殘差是實際觀察值與回歸估計值的差。從殘差圖可以看出數據的殘差離零點的遠近，當殘差的置信區間均包含零點，說明回歸模型能較好的符合原始數據，否則視為異常點。

對1 140組實驗數據進行殘差分析后的殘差圖如圖3所示，由此可以確定殘差落在其置信區間內的大致位置，也可以觀察殘差的分布變化的趨勢，殘差圖越散亂代表模型的適配越好[16]。經分析，異常點主要分布在35 ℃、13%水分下儲藏5個月后和35 ℃、13.5%水分下儲藏4個月后的數據點，以及高溫高水分儲藏條件下的儲藏初期數據點，共計44組數據。這些異常數據中，高溫低水分區(13.0%和13.5%)真菌孢子數量基本處于檢測方法的最低檢出限附近，檢測結果誤差偏大，高溫高水分區(17.9%)，儲糧真菌生長速度較快，10 d的取樣頻率，無法檢測到真菌孢子數量逐漸升高的趨勢，因此初期檢測數據波動較大，影響模型的準確率。經過一次殘差分析，剔除異常點后，模型的擬合度R2從0.72上升到0.77。若經過多次篩選完全剔除異常點后，擬合優度能達到0.84，但此時的結果是為了達到數學上的最優化而剔除了一部分符合實際的實驗數據，可能影響模型的真實性，因此選擇第一次剔除異常點后的數據點進行擬合建模。

2.3 實倉檢測數據驗證

為了便于對真菌生長預測模型在實際應用中預測效果進行評價，根據標準“LS/T 6132 糧食檢驗 儲糧真菌的檢測 孢子計數法”[17]附錄C“儲糧安全評價參考表”，將危害真菌孢子檢出數量分為4個級別，詳見表1。在實際儲藏中，儲糧樣品真菌孢子檢出數量基本可代表糧食樣品霉變程度，依據參考表中級別對儲糧安全狀況進行初步判定，進而指導相應處置措施。

表1 儲糧安全評價參考表

實倉檢測數據來源于華北地區某糧庫，實驗倉詳細儲糧信息及采樣方法見方法1.3.2。檢測時間從6月到10月，對應糧食儲藏時間為150 ～ 255 d，溫度范圍為19.0～ 27.4 ℃，水分范圍為12.8% ～ 15.4%，共計84組實倉檢測數據，根據實倉測得的溫度、稻谷含水量和儲藏時間，采用式(2)對實倉儲糧真菌孢子數進行預測，實測數據與預測數據結果見表3。

由于微生物生長檢測方法本身誤差很大，對真菌孢子數量進行預測，預測值與實測值在同一個數量級以內，不影響儲糧安全級別評價，可指導合理的應急處置措施，即認為可以接受。實測數據與預測數據結果如表2所示，84組實倉數據中，有70組數據在同一個數量級內，對儲糧安全評價級別在同一級內，即對各點儲糧真菌危害程度預測正確率為83.3%。由此可見，通過多元線性回歸方法得到的儲糧真菌生長數量預測模型為實倉儲糧安全狀況預測提供了一個新的方法和途徑。

圖3 第一次殘差分析結果

表2實倉檢測數據與預測數據比較

日期6月1日7月15日8月1日8月12日8月26日9月21日10月7日6月1日7月15日8月1日8月12日8月26日9月21日10月7日取樣點真菌孢子數/105個/g實測值預測值10.00.00.00.30.30.00.30.10.20.50.41.31.21.720.00.00.30.00.00.30.90.20.61.20.91.91.93.630.00.30.31.83.00.02.70.10.30.60.72.50.72.840.00.00.01.51.811.413.80.41.73.83.614.211.620.353.37.211.78.77.27.814.71.53.56.45.75.09.217.660.00.00.00.31.59.39.00.52.02.72.98.25.98.670.00.60.90.05.717.117.70.42.34.13.815.015.122.980.90.30.61.22.72.72.71.22.75.05.04.34.59.890.00.30.00.93.011.719.20.62.43.51.39.99.720.5100.91.53.34.29.624.919.81.35.49.617.632.717.538.0117.88.418.37.57.26.97.82.64.97.010.112.512.616.3121.51.22.75.46.312.015.92.49.816.827.051.959.381.9

本研究通過模擬儲藏條件得到的儲糧真菌孢子數量靜態預測模型，但在實際倉儲環境中，由于糧堆體積較大，不同季節環境溫濕度的變化，與實驗室模擬的儲藏條件存在較大差異，模型預測結果仍存在一定偏差。因此，有待于通過大量實倉檢測數據反饋驗證，優化模型算法形成新的動態預測模型，模型預測的準確率會進一步提高。

3 結論

以多元統計分析作為基礎與前提，利用MATLAB軟件對1 140組模擬儲藏稻谷的溫度、水分、儲藏時間及取對數后的真菌孢子數進行多元線性回歸分析，檢驗、分析多個自變量對因變量的綜合線性影響的顯著性，建立了多元線性回歸模型應用于儲糧真菌生長數量預測。

經殘差分析剔除異常點后得到多元線性模型：

lny=-20.787+0.157×x1+0.027×x2+1.683×x3

多元線性擬合優度R2=0.77，F檢驗的統計量值為1 219.552，且顯著性概率為0，結果表明回歸模型總體效果顯著；環境溫度、儲藏時間和稻谷含水量的t統計量分別為24.785、27.175、46.607，各項參數對取對數后的儲糧真菌孢子數有顯著影響。由多元線性回歸模型的系數可知，對稻谷儲糧真菌孢子數量影響最大是稻谷含水量，其次是儲藏溫度和儲藏時間。

通過對多元線性回歸方程進行指數變換，可得到儲糧真菌孢子數的預測模型:

y=exp(-20.787+0.157×x1+0.027×x2+1.683 ×x3)

為了探究真菌孢子數量模型在實際應用中的預測效果，利用實倉數據對模型進行初步驗證，以儲糧安全等級作為評價標準，儲糧真菌危害程度預測的正確率為83.3%。但仍有待于經過大量實倉檢測數據驗證，優化算法建立新的動態預測模型，進一步提高儲糧安全狀況預測的正確率。