模型思想視角下“角的比較與運算”設計研究

陳海烽

[摘 ?要] 文章以“角的比較與運算”為例，闡釋模型思想這一視角在設計中的運用. 對于角度的和與差，抽象出有公共端點的三條射線組成的模型這個結構，進而繼續模型化，可得到更一般的結構，那就是整體等于部分之和的模型.？搖此設計經過實踐后取得了良好的教學效果.

[關鍵詞] 模型思想;設計;實驗

“角的比較與運算”是人教版《義務教育教科書·數學》七年級上冊第四章第三節“角”的第二小節的第一課時，學生在此之前學習了線段的比較與運算、線段的中點，且已經知道了角的定義、角的表示方法和角的度量. 此內容是學生今后學習角平分線、角的代數運算等內容的奠基課，所以非常重要. 研究者在廈門市第六屆課堂教學創新大賽中展示本節課，用模型思想的視角來演繹，取得了良好的教學效果，現整理成文，供大家討論、交流.

對模型思想的再認識

《義務教育數學課程標準（2011年版）》（以下簡稱《課標》）中十大關鍵詞對模型思想的定義是：“模型思想的建立是學生體會和理解數學與外部世界聯系的基本途徑. 建立和求解模型的過程包括：從現實生活或具體情境中抽象出數學問題，用數學符號建立方程、不等式、函數等表示數學問題中的數量關系和變化規律，求出結果并討論結果的意義. ”模型思想是一種基本的數學思想，是《課標》里明確提出的十個核心概念中唯一以“思想”冠名的概念.

沈文選指出，“數學模型可以描述為……運用適當的數學工具，得到的一個數學結構”“數學模型……也包括……數學概念、各種數學公式、方程式、定理、理論體系等”.

研究者主要是為了得到一個良好的數學結構，用數學的符號建立一個基本角度的和與差的運算模型.

教學設計

1. 教學目標設計

（1）通過動手實驗、討論、展示，知道角的比較大小的兩種方法——度量法和疊合法，從中感悟角的和與差的運算模型.

（2）利用一副三角板拼湊角度，通過實驗的觀察和討論，知道拼三角板的本質就是兩個角度的和與差.

（3）通過幾何畫板的演示，抽象出具體角的和與差的基本模型，能從基本圖形位置關系中提煉角度之間的和與差的數量關系模型.

（4）通過對基本模型進行不斷變化的過程，讓學生從特殊到一般，知道角度之間和與差的運算，能初步運用模型解決問題.

（5）通過基本模型的變式，提高學生關于角度和與差的運算能力.

2. 教學過程設計

（1）溫故知新，引出課題

教師：三角板是我們的朋友，今天我們一起來“玩轉三角板”.

問題1：你能說出老師手上這個三角形中這兩個角的大小嗎？

追問：你是如何知道的？

問題2：度量法要注意些什么呢？

追問：要知道這兩個角的大小，除了度量法，還有別的方法嗎？

問題3：你是如何想到疊合法的？是受什么得到的啟發？角度的疊合要注意些什么？

問題4：你知道角的大小比較中的道理嗎？

師生活動：學生回憶三角板的相關知識，通過操作、實驗發現了度量法和疊合法，教師讓學生展示和交流.

教師關注：對于學生的認知，教師給予相應的回應，同時引導學生通過類比的方法獲知學生的最近發展區，引導學生從物理模型到數學圖形的過渡.

設計意圖？搖 從與學生相處多年的三角板入手，能讓學生獲得親近感;從特殊角度之間的大小比較，過渡到一般角度的大小比較，能讓學生第一次感知從特殊到一般，從而為抽象出角度的和與差的基本模型做準備.

（2）動手操作，探究新知

問題5：我們剛才比較了兩個角度（60°和45°）之間的大小，你知道這兩個角度之間差了多少度嗎？你能否把差的角度拼出來？

追問1：你能否再用這副三角板拼疊出那些度數的角？這些角有什么規律？

追問2：為什么這些角都是15°的倍數？你能說出理由嗎？

師生活動：學生動手操作，小組合作探究，師生歸納.

師生歸納：可以拼出很多的角. 還可以拼出15°，75°，105°，120°，135°，150°，165°，180°.

設計意圖？搖 三角板的拼角游戲，能讓學生對特殊的角度之間有一個良好的認識，能鍛煉學生對角度大小的估計能力和動手操作能力，能加深學生對角的識別能力，且能讓學生初步奠定“拼與和的運算對應，疊與差的運算對應”的經驗基礎.

（3）提煉模型，應用新知

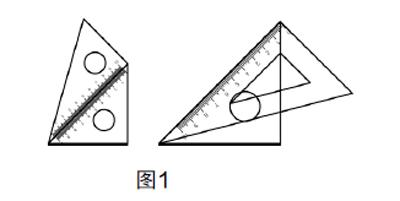
問題6：通過對三角板進行拼接，我們獲得了不少角度. 下面我們繼續觀察拼出75°和15°這兩個角度的圖形. 如圖1，老師的三角板和你們的“大小”不同，為什么拼疊出的角度是一樣的？

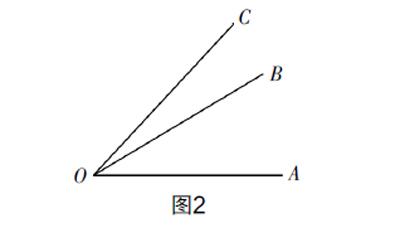
追問1：圖1的兩個圖形和圖2有什么地方是一致的？

追問2：老師將上述兩種拼法圖形化，然后將題一般化，獲得如圖2所示的模型. 你能告訴我它們之間的和差關系嗎？

追問3：這個和差關系的模型能否用文字語言來描述？

追問4：這個模型能否用整體、部分的關系來描述？

設計意圖？搖 從上一環節拼三角形的特殊角度出發，獲知角度和與差的基本模型，使得教學銜接更加自然，促使學生從實物到圖形到文字進而到語言之間的良好轉化，引導學生從具體到抽象，加深對角度和與差的理解. 第二次從特殊到一般，直接抽象出現有的模型，引導學生對模型進行表達——有公共端點的三條射線就是對角度和與差的模型的最簡圖形表達. 接著，教師引導學生從整體到部分，提煉出更一般的加法模型，使得學生的認知能力有質的提升.

（4）變式訓練，固化模型

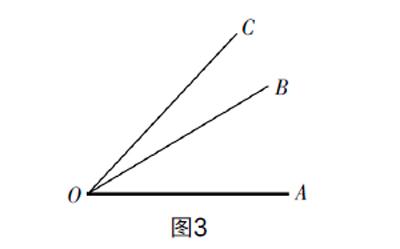
問題7：如圖3，∠AOC=45°，∠AOB=30°，求∠BOC的大小.

變式1：如圖3，∠AOC=45°，∠AOB=26°34′，求∠BOC的大小（此題系廈門中考題改編）.

變式2：課本例1.

變式3：如圖3，（幾何畫板演示拖動）∠AOC=180°，銳角∠AOB=x°，求∠BOC的大小（用含x的代數式表示）.

變式4：已知∠AOC=45°，∠AOB=30°，求∠BOC的大小.

變式5：如圖4，∠AOB=∠_____-∠_____=∠_____-∠_____，∠AOC=∠_____-∠_____=∠_____+∠_____.

變式6：你能根據圖4寫出結果等于∠BOD的和差算式嗎？

變式7：如果老師再增加一條射線，如圖5，你還能寫出幾個結果等于∠BOD的和差算式？

師生活動：教師示范，學生答題并展示.

教師關注：學生答題是否嚴謹、規范.

設計意圖 ？搖從特殊角度的計算，過渡到一般角度的計算，再到式子的表達，再次體現了從特殊到一般，從具體到抽象. 為了對思維進行不斷的提升，研究者從有配圖到無配圖，這一過程體現了分類討論思想. 且計算時，不僅鞏固了度、分、秒的運算，還將其與十進制的加減法進行類比，體現了類比思想.

（5）方法總結，優化結構

教師：我們一起來回顧一下本節課的學習方法.

問題8：對于角的大小比較，我們是如何學習的？

問題9：對于角的和差運算，我們是如何學習的？

追問：從學習過程中，我們可以獲得什么樣的學習經驗？

師生活動：教師和學生共同回憶并整理本節知識的學習流程.

教師關注：學生的表現以及邏輯表達.

設計意圖？搖 通過對整堂課的梳理，學生再次回憶學習過程，明晰研究流程，從中獲得了學習經驗，提高了對整節課的結構把握，同時內化為了自己的知識，能站在模型思想的角度看待數學問題，這有利于培養學生更加深邃的數學眼光.

教學反思

1. 動手實驗，感知模型？搖

數學教育家波利亞曾指出，數學具有兩個面，以歐幾里得方向表現出來的數學看上去是一種系統演繹的科學，但在形成過程中的數學看上去卻是一種實驗性的歸納科學. 數學實驗是學生在運用有關工具（如學具、計算機、數學軟件等）時，在數學思維活動的參與下，通過手腦并用，借助觀察、模仿、實驗、猜想等手段獲得體驗，構建發展學生數學認知結構的素養型活動. 從引導學生觀察圖形入手，感知拼疊角度，進而感知角度的和與差的基本圖形，這一認識不是書本或教師告知的，而是學生透過現象，發揮自己的洞察力分析得到的. 此處以發展學生的洞察力，尋求解決問題的方法為主要目標. 角度的拼疊再次讓學生經歷觀察、比較、推理、交流等活動，進一步培養了學生的洞察力，發展了學生的創新意識. 學生的上課表現，說明學生對模型的感知是到位的.

2. 活用畫板，抽象模型

《課標》指出：要加強信息技術在數學學習的整合. 本節課，學生通過三角板拼出各種角度，感知各個角度的變化情況，然后通過觀察，得出本質——由公共端點的三條射線組成的模型. 研究者通過幾何畫板引導學生觀察，讓學生去除非本質的東西，抽象出有用的數學模型，體現了從具體到抽象的數學思想. 同時在變式3、變式4的教學過程中，研究者再用幾何畫板的功能，給予學生強烈的震撼，這能加深學生對模型的進一步理解.

3. 類比推理，同化模型

在本課的設計中，研究者用到了如下類比：一是角度的比較和線段的比較相類比，二是線段的和差運算和角度的和差運算相類比，三是角度的加減運算和十進制的加減運算相類比. 這些類比的本質就是同化，有利于學生數學素養的提升. 《課標》指出：數學素養是現代社會每個公民應該具備的基本素養. 其中的素養至少包含三個方面的含義，一是用數學的眼光審視生活;二是在生活中養成積累數學活動經驗的習慣;三是在不斷聯系數學與生活的過程中自覺鍛煉思維能力和應用能力. 本節課從學生最常見的三角板入手，讓學生知道數學就在我們身邊，而且可能就在我們經常忽視的地方存在著，需要我們重新去審視，引導學生用數學的眼光去審視三角板的各種用途. 同時就拼疊過程積累數學活動經驗，抽象出有公共端點的三條射線這一基本角度和差數學模型，并將此模型加以應用，引導學生從比較抽象的問題中聯想、轉化為我們已經解決過的數學問題，以達到思維暢通.

4. 變式訓練，活用模型

抽象出有公共端點的三條射線這一模型之后，研究者設置了幾道題加以運用. 問題7是從特殊的角度入手，讓學生體會到運算其實很簡單，以增強學生學習的自信心. 教學過程中，變式1加入了不同單位的角度直接運算，此時的難點是60進制的體會. 等學生完成后，研究者分析講解，接著通過幾何畫板進行動態演示，進入書本習題，即變式2，體現了一個動態的研究過程，以讓學生掌握角的運算. 變式3是研究者給定了一個參數，讓學生體會其與一元一次方程的關聯;接著研究者將圖撤掉，得到變式4，讓學生在腦中畫圖，使得原有的經驗得以升華. 而變式5和變式6則主要是訓練學生將復雜圖形化歸為基本模型的能力.

結束語

對于“角的比較與運算”這一課，多數設計者沒有從模型的角度去思考. 不少教師認為，這個問題比較簡單，不值得花時間，于是往往通過大量的訓練去強化角度的和差運算，甚至把這節課當成一堂習題課. 這種做法的背后其實存在著對一節課價值判斷的問題，值得我們深思.