電壓源型直流輸電變流器系統動態面反步控制

胡成江　劉加朋　于金鵬　于海生

摘要：? 針對傳統反步控制方法中存在的問題，本文主要對電壓源型直流輸電變流器電網側變流器系統的有功/無功功率控制問題進行研究。首先引入了反步控制方法，將高階系統處理為3個低階子系統，并針對每個子系統設計了控制律，實現對整個系統的控制。其次，由于傳統反步控制方法中存在的“計算爆炸”問題，本文通過引入動態面控制技術解決。在本文控制方法下設計的控制器，不需要有功/無功功率高階導數的信息，且控制器結構簡單。為驗證本文所提出的VSC-HVDC變流器系統的動態面反步控制方法的有效性，在Matlab/Simulink環境下進行仿真實驗。仿真結果表明，在本文控制方法下，系統有功功率和無功功率可以準確跟蹤其設定值，而且與傳統反步控制方法相比，在本文提出的控制方法下，電網側變流器系統具有更好的動態響應，說明本文提出的方法具有調節速度快、誤差小的優勢。該研究對VSC-HVDC系統的控制具有重要意義。

關鍵詞：? 反步控制; 動態面控制; 高壓直流輸電; 變流器; 功率控制; 控制器設計

中圖分類號： TM721.1; TM46文獻標識碼： A

隨著當代能源需求的不斷增長，海上風力發電技術發展迅速，相比于傳統的火力發電，海上風力發電具有發電過程環保、不占用陸地資源和轉換率高等優勢[13]。目前，海上風力發電并網大部分采用電壓源型直流輸電變流器（voltage source converter based high voltage direct current transmission， VSC-HVDC）。Zhang G等人[4]建立并研究了VSC-HVDC系統的穩態模型，其所提出的控制方法沒有考慮VSC-HVDC系統的動態響應特性，因此，研究VSC-HVDC系統動態模型的控制問題具有重要意義。為了實現更好的控制效果，學者們將滑模控制技術[56]、自適應控制技術[78]、反步控制方法[911]和一些其他的控制技術[1217]應用到高階系統的控制研究中。反步控制方法是處理高階系統的有效方法，吳杰等人[12]將反步控制方法應用到VSC-HVDC電網側變流器系統的功率控制中，相比于傳統的雙閉環矢量控制方法，在反步控制方法下，VSC-HVDC變流器系統的動態響應速度快。然而VSC-HVDC變流器系統反步控制方法存在兩個主要缺點：一是傳統反步控制方法的控制器設計過程需要對控制律進行反復求導，從而產生“計算爆炸”的問題;二是在傳統反步控制方法在處理高階系統時，控制器設計過程中需要功率信號的高階導數信息[12]，上述問題導致傳統反步控制方法在實際工程中的應用范圍受到限制。基于此，本文提出了一種VSC-HVDC變流器系統動態面反步控制方法，將基于動態面技術的反步控制方法應用到VSC-HVDC變流器系統的控制中，通過引入動態面控制方法[1820]，解決了傳統反步控制方法中存在的兩個主要缺點。本文提出的控制方法可保證VSC-HVDC變流器系統的功率控制誤差收斂到一個足夠小的鄰域內。

1 VSC-HVDC系統的數學模型

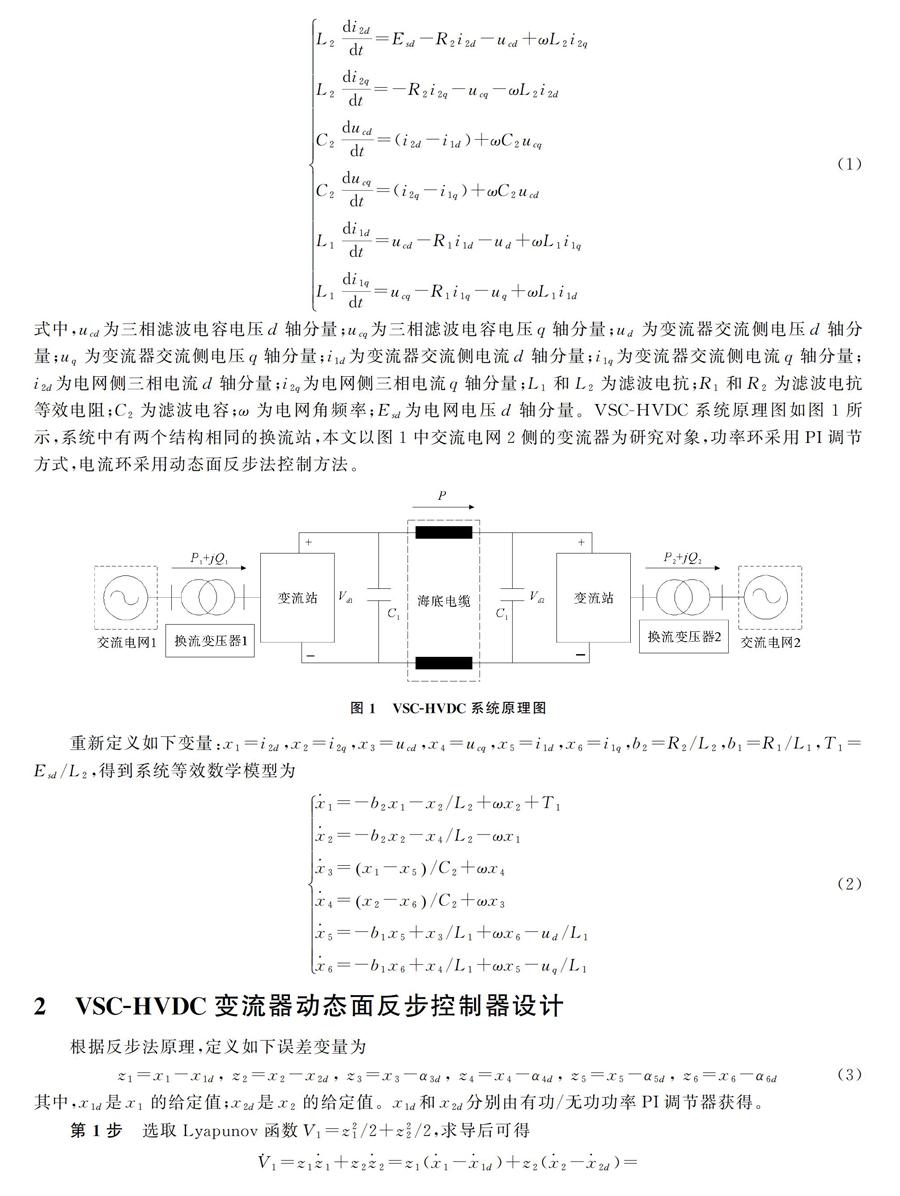
式中，ucd為三相濾波電容電壓d軸分量;ucq為三相濾波電容電壓q軸分量;ud為變流器交流側電壓d軸分量;uq為變流器交流側電壓q軸分量;i1d為變流器交流側電流d軸分量;i1q為變流器交流側電流q軸分量;i2d為電網側三相電流d軸分量;i2q為電網側三相電流q軸分量;L1和L2為濾波電抗;R1和R2為濾波電抗等效電阻;C2為濾波電容;ω為電網角頻率;Esd為電網電壓d軸分量。VSC-HVDC系統原理圖如圖1所示，系統中有兩個結構相同的換流站，本文以圖1中交流電網2側的變流器為研究對象，功率環采用PI調節方式，電流環采用動態面反步法控制方法。

2VSC-HVDC變流器動態面反步控制器設計

根據反步法原理，定義如下誤差變量為

z1=x1-x1d， z2=x2-x2d， z3=x3-α3d， z4=x4-α4d， z5=x5-α5d， z6=x6-α6d（3）

其中，x1d是x1的給定值;x2d是x2的給定值。x1d和x2d分別由有功/無功功率PI調節器獲得。

第1步選取Lyapunov函數V1=z21/2+z22/2，求導后可得

1=z11+z22=z1（1-1d）+z2（2-2d）=

z1（-b2x1-α3d-α3L2-z3L2-α3L2+ωx2+T1-1d）+z2（-b2x2-α4d-α4L2-z4L2-α4L2+ωx1-2d）（4）

本文中電網電壓d軸分量是一個有界值，由T1的定義可知，T1是一個有界的值，且滿足T1≤d。由楊氏不等式可得

z1T1≤12ε21z21+12ε21d2（5）

其中，ε1是一個任意小的正數。引入新的狀態變量α3d和α4d，使α3和α4分別通過時間常數為ε3和ε4的動態面濾波器，即

ε33d+α3d=α3， α3d（0）=α3（0）

ε44d+α4d=α4， α4d（0）=α4（0）（6）

其中，α3d和α4d是濾波器的輸出信號。將式（5）代入式（4）可得

1≤z1（-b2x1-α3d-α3L2-z3L2-α3L2+ωx2-1d+12ε21z1）+

z2（-b2x2-α4d-α4L2-z4L2-α4L2+ωx1-2d）+12ε21d2（7）

構造虛擬控制律α3和α4，即

α3=L2（k1z1-b2x1+ωx2-1d）

α4=L2（k2z2-b2x2-ωx1-2d）（8）

其中，k1=+12ε21，>0，k2>0。將式（8）代入式（7）可得

1≤-k1z21-k2z22-z1（α3d-α3）L2-z2（α4d-α4）L2-z1z3L2-z2z4L2+12ε21d2（9）

第2步選取Lyapunov函數V2=V1+z23/2+z24/2，求導后可得

2=1+z33+z44=1+z3x1C2-x5C2+ωx4-3d+z4x2C2-x6C2-ωx3-4d（10）

引入新的狀態變量α5d和α6d，使α5和α6分別通過時間常數為ε5和ε6的動態面濾波器，即

ε55d+α5d=α5， α5d（0）=α5（0）

ε66d+α6d=α6， α6d（0）=α6（0）（11）

其中，α5d和α6d是濾波器的輸出信號。將式（6）代入式（10）可得

2=1+z3x2C2-z1L2-α5d-α5C2-z5C2-α5C2+ωx4+α3d-α3ε3+

z4x1C2-z2L2-z6C2-α6d-α6C2-α6C2-ωx3+α4d-α4ε4（12）

構造虛擬控制律α5和α6，即

α5=C2（k3z3+x1/C2-z1/L2+ωx4）

α6=C2（k4z4+x2/C2-z2/L2-ωx3）（13）

其中，k3>0，k4>0。將式（13）代入式（12）可得

2≤-k1z21-k2z22-k3z23-k4z24-z1（α3d-α3）L2-z2（α4d-α4）L2-z3（α5d-α5）C2-z4（α6d-α6）C2+

z3（α3d-α3）ε3+z4（α4d-α4）ε4-z3z5C2-z4z6C2+12ε21d2（14）

第3步選取Lyapunov函數V3=V2+z25/2+z26/2，求導后可得

3=2+z55+z66=

∑4i=1-kiz2i-z1（α3d-α3）L2-z4（α6d-α6）C2-z2（α4d-α4）L2-z3（α5d-α5）C2+12ε21d2+

z3（α3d-α3）ε3+z4（α4d-α4）ε4+z5-b1x5+x3/L1+ωx6-ud/L1+α5d-α5ε5+

z6-b1x6+x4/L1+ωx5-uq/L1+α6d-α6ε6-z3z5C2-z4z6C2（15）

選取系統的真實控制律為

ud=L1（k5z5-b1x5+x5/L1+ωx6-z3/C2）

uq=L1（k6z6-b1x6+x4/L1-ωx5-z4/C2）（16）

其中，k5>0，k6>0。

文獻[12]中提出的反步控制方法沒有考慮控制器設計過程中因對控制律反復求導而產生“計算爆炸”的問題，由式（16）可知，本文引入了動態面濾波器，解決了傳統反步法中存在的“計算爆炸”問題，從而簡化了控制器的結構。

3穩定性證明

將式（16）代入式（15），可得

3≤∑6i=1-kiz2i-z1（α3d-α3）L2-z2（α4d-α4）L2-z3（α5d-α5）C2-z4（α6d-α6）C2+

z3（α3d-α3）ε3+z4（α4d-α4）ε4+z5（α5d-α5）ε5+z6（α6d-α6）ε6+12ε21d2（17）

定義動態面濾波器誤差為

y3=α3d-α3， y4=α4d-α4

y5=α5d-α5， y6=α6d-α6（18）

將式（6）和式（11）代入式（18），可得

3=-α3d-α3ε3-3=-y3ε3+D3， 4=-α4d-α4ε4-4=-y4ε4+D4

5=-α5d-α5ε5-5=-y5ε5+D5， 6=-α6d-α6ε6-6=-y6ε6+D6（19）

其中，D3=-3;D4=-4;D5=-5;D6=-6。

由文獻[19]可知，D3，D4，D5和D6在緊集Ωi，（i=3，4，5，6）上具有最大值DiM，即Di≤DiM。由此，得不等式為

yii≤-y2i/εi+DiMyi≤-y2i/εi+12τD2iMy2i+τ2（20）

其中，i=3，4，…，6;τ>0。由楊氏不等式可得

-y3z1L2≤y23/4L2+z21/L2， -y4z2L2≤y24/4L2+z22/L2

-y5z3C2≤y25/4C2+z23/C2， -y6z4C2≤y26/4C2+z24/C2

y3z3ε3≤y23/4ε3+z23/ε3， y4z4ε4≤y24/4ε4+z24/ε4

y5z5ε5≤y25/4ε5+z25/ε5， y6z6ε6≤y26/4ε6+z26/ε6（21）

為了證明整個系統的穩定性，選取系統的Lyapunov為：V=V3+y23/2+y24/2+y25/2+y26/2，對V求導，得

≤∑6i=1-kiz2i-z1L2y3-z2L2y4-z3C2y5-z4C2y6+z3ε3y3+z4ε4y4+z5ε5y5+

z6ε6y6+12ε21d2+y33+y44+y55+y66（22）

將式（20）和式（21）代入式（22），可得

≤∑6i=1-kiz2i+y234L2+z21L2+y244L2+z224L2+y254C2+z23C2+y264C2+z24C2+y234ε3+z23ε3+

y244ε4+z24ε4+y254ε5+z25ε5+y264ε6+z26ε6-y23ε3+12τD23My23+τ2-y24ε4+τ2-y26ε6+

12τD24My24-y25ε5+12τD25My25+12τD26My26+τ2+τ2+12ε21d2≤-aV+b（23）

其中，a=min2k1-1L2，234ε3-14C2-12τD23M，2k2-1L2，2k3-1C2-1ε3，2k4-1C2-1ε4，234ε4-

14L2-12τD24M，2k5-1ε5，234ε5-14C2-12τD25M，2k6-1ε6，234ε6-14C2-12τD26M;b=2τ+12ε21d2。由式（23）可得

Vt≤V（t0）-bae-a（t-t0）+ba≤V（t0）+ba，t≥t0（24）

式（24）表明，zi（i=1，2，3，4，5，6）屬于緊集Ω={（vi，）V≤V（t0）+b/a，t≥t0。由式（24）可求得[19]limt→∞zi≤2b/a。當選定參數ki，ε3，ε4，ε5和ε6，選取足夠小的τ和ε1，可以保證系統的跟蹤誤差zi足夠小。

4仿真分析

為驗證本文所提出的VSC-HVDC變流器系統的動態面反步控制方法的有效性，在Matlab/Simulink環境下進行仿真實驗。實驗過程中，對參數進行標幺化。系統模型中選定的參數為：L1=0.006 H，L2=0.001 7 H，C2=0.000 06 F，R1=0.25 Ω，R2=0.25 Ω，Esd=35 kV。

選取控制器參數為：k1=38 500，k2=2 600，k3=555，k4=660，k5=99 800，k6=140 000，ε4=0.001 8，ε3=0.05，ε5=0.833 3，ε6=0.004 4。

選取PI調節參數為：Kp1=Kp2=900，Ki1=Ki2=1 000。

選擇有功功率的設定值為：Pr=0.4 MW， 0≤t≤1

0.8 MW， t>1。

選擇無功功率給定的設定值為：Qr=0.2 MVar， 0≤t≤1

0.4 MVar， t>1。

在本文控制方法下，有功功率跟蹤曲線如圖2所示，無功功率跟蹤曲線如圖3所示。圖2和圖3中，P1為系統有功功率響應，Pr為系統有功功率期望值，其初始值為0，Q1為系統無功功率響應曲線。由圖2可以看出，系統有功功率可以準確跟蹤其期望值;由圖3可以看出，系統無功功率可以準確跟蹤其期望值。

在本文動態面反步控制方法下，系統的功率跟蹤誤差曲線如圖4所示，由圖4可以看出，系統的功率調節誤差在0.006 s時收斂;在傳統反步控制方法下，系統的有功功率跟蹤曲線如圖5所示，圖5中，Pb為傳統反步控制方法下系統的有功功率響應曲線，由圖5可以看出，系統有功功率在0.02 s時能夠跟蹤其期望值。

在傳統反步控制方法下，系統的無功功率跟蹤曲線如圖6所示，圖6中，Qb為傳統反步控制方法下系統的無功功率響應曲線，由圖6可以看出，系統有功功率在0.025 s時能夠跟蹤其期望值;在傳統反步控制方法下，系統的功率跟蹤誤差曲線如圖7所示，圖7與圖5相比可知，本文提出的方法具有調節速度快、誤差小的優勢。

在本文控制方法下，x1和x1d跟蹤曲線如圖8所示，x2和x2d跟蹤曲線如圖9所示，由圖8和圖9可以看出，x1和x2可以快速的跟蹤期望值。x1和x2跟蹤誤差曲線如圖10所示，由圖10可以看出，在本文控制方法下，系統的跟蹤誤差能夠快速的穩定到零點附近的小鄰域內。

為了驗證在實際工程中缺少功率給定值的高階導數信息時，本文所提出的控制方法仍然有效，在仿真實驗中，重新選取功率的設定值為

在本文控制方法下，系統的有功功率跟蹤曲線如圖11所示，系統的無功功率跟蹤曲線如圖12所示。圖11中，P1為系統有功功率響應，Pr為系統有功功率期望信號，其初始值為0。由圖11可以看出，系統的有功功率可以快速準確跟蹤其期望值。圖12中，Q1為系統無功功率響應曲線，Qr為系統無功功率期望值，其初始值為0，由圖12可以看出，系統的無功功率可以準確跟蹤其期望值。在動態面反步控制下，系統的功率跟

蹤誤差曲線如圖13所示，由圖13可以看出，系統的功率調節誤差在0.004 s時刻收斂。在傳統反步控制方法下設計的控制器，需要功率信號的高階導數信息，由圖11～圖13可知，本文提出的經過改進的反步控制方法，在功率信號高階導數不存在的情況下，仍能實現有功功率和無功功率的快速協調控制。

5結束語

本文將反步控制方法與動態面控制技術相結合，實現了對VSC-HVDC變流器系統的有功/無功功率協調控制。引入反步控制方法解決了高階系統控制器設計復雜困難的問題。采用動態面技術解決了傳統反步控制方法中存在的“計算爆炸”問題，從而控制器的結構得以簡化。同時，動態面控制技術克服了傳統反步方法控制器設計過程中需要功率給定值的高階導數信息問題。仿真結果表明，本文所提出的控制方法能夠有效實現對電壓源型高壓直流輸電變流器系統功率的協調控制，并可根據需要提供一定容量的無功功率補償。

參考文獻：

[1]Wang Q， Yu Z P， Ye R， et al. An ordered curtailment strategy for offshore wind power under extreme weather conditions considering the resilience of the grid[J]. IEEE Access， 2019（7）： 5482454833.

[2]Erlich I， Shewarega F， Feltes C， et al. Offshore wind power generation technologies[J]. Proceedings of the IEEE， 2013， 101（4）： 891905.

[3]Vos K D， Driesen J， Belmans R. Assessment of imbalance settlement exemptions for offshore wind power generation in Belgium[J]. Energy Policy， 2011， 39（3）： 14861494.

[4]Zhang G B， Zheng X. Steady-state model for VSC based HVDC and its controller design[C]∥Power Engineering Society Winter Meeting. Hangzhou： IEEE， 2001.

[5]陳創庭， 周志成， 陳俊武. 滑模變結構控制在高壓直流輸電系統上的應用研究[J]. 廣東電力， 2006， 19（11）： 15.

[6]游國棟， 李繼生， 侯勇， 等. 單相光伏并網逆變器的反步滑模控制策略[J]. 電網技術， 2015， 39（4）： 916923.

[7]Ahmad S， Khan L. Adaptive feedback linearization based HVDC damping control paradigm for power system stability enhancement[C]∥2016 International Conference on Emerging Technologies. Islamabad， Pakistan： IEEE， 2017.

[8]胡亞強， 于金鵬， 趙林， 等. 基于命令濾波技術的水下機器人位置跟蹤控制[J]. 青島大學學報： 工程技術版， 2019， 34（1）： 95100.

[9]王寶華， 蔣力. 基于精確反饋線性化的直流微電網雙向直流變流器反步滑模控制[J]. 電力系統保護與控制， 2018， 46（2）： 4349.

[10]Zhao X D， Li K. Control of VSC-HVDC for wind farm integration based on adaptive backstepping method[C]∥IEEE International Workshop on Intelligent Energy Systems. Vienna， Austria： IEEE， 2014.

[11]楊俊華， 陳凱陽， 王秋晶， 等. 電壓源型高壓直流輸電系統的反步變結構控制[J]. 控制理論與應用， 2014， 31（11）： 15481554.

[12]吳杰， 王志新， 王國強， 等. 電壓源型直流輸電變流器系統中電網側變流器的反步法控制[J]. 控制理論與應用， 2013， 30（11）： 14081413.

[13]Yu J P， Shi P， Dong W J， et al. Observer and command filter-based adaptive fuzzy output feedback control of uncertain nonlinear systems[J]. IEEE Trans on Industrial Electronics， 2015， 62（9）： 59625970.

[14]康忠健， 張梓霖， 李鑫， 等. MMC-HVDC系統的模糊PI優化控制[J]. 浙江電力， 2019， 38（8）： 5964.

[15]Chen X， Wang L， Sun H S， et al. Fuzzy logic based adaptive droop control in multi-terminal HVDC for wind power integration[J]. IEEE Transactions on Energy Conversion， 2017， 32（3）： 12001208.

[16]黃俊銘， 朱建全， 莊遠燦. 基于動態RBF神經網絡的廣義電力負荷建模[J]. 電網技術， 2018， 42（2）： 591597.

[17]Schnleber K， Collados C， Pinto R T， et al. Optimization-based reactive power control in HVDC-connected wind power plants[J]. Renewable Energy， 2017， 109： 500509.

[18]Swaroop D， Gerdes J C， Yip P P， et al. Dynamic surface control of nonlinear systems[C]∥American Control Conference. Albuquerque， NM， USA： IEEE， 1997.

[19]Yu J P， Shi P， Dong W J， et al. Neural network-based adaptive dynamic surface control for permanent magnet synchronous motors[J]. IEEE Transactions on Neural Networks and Learning Systems， 2015， 26（3）： 640645.

[20]張國斌， 于金鵬， 于海生， 等. 永磁同步電機模糊離散調節控制[J]. 電機與控制應用， 2019， 46（4）： 17.

Dynamic Surface Backstepping Control for Voltage Source

Converter-High Voltage Direct Current Transmission Converter SystemsHU Chengjiang， LIU Jiapeng， YU Jinpeng， YU Haisheng

（School of Automation， Qingdao University， Qingdao 266071， China）Abstract：? In view of the problems existing in the traditional backstepping control method， this paper mainly studies the active/reactive power control of the grid side converter systems of voltage source converter based high voltage direct current transmission converter. First， the backstepping control method is introduced to treat the high-order system as three low-order subsystems， and then the control laws are designed for each subsystem to realize the control of the whole system. Secondly， due to the fact that the problem of “explosion of complexity” exists in the traditional backstepping control method， this paper introduces the dynamic surface control technology to overcome the problem of “explosion of complexity”. The controller designed in this paper does not require the information of high order derivative of active/reactive power， at the same time， the structure of the controller in this paper is simple. Finally， the simulation experiments are carried out in Matlab/Simulink environment to verify the effectiveness of the dynamic surface backstepping control method proposed in this paper. The simulation results show that under the control method in this paper， the active power and reactive power can accurately track their set values. The control method proposed in this paper has better dynamic response compared with the traditional control method. The method proposed in this paper has the advantages of fast regulation speed and small error， which is of great significance to the control of VSC-HVDC systems.

Key words：? backstepping control; dynamic surface control; VSC-HVDC; converter; power control; controller design

收稿日期： 2019-12-16; 修回日期： 2020-02-03

基金項目：? 國家重點研發計劃（2017YFB1303503）;國家自然科學基金資助項目（61973179，61573203）;泰山學者工程專項經費資助（TSQN20161026）

作者簡介：? 胡成江（1994-），男，碩士研究生，主要研究方向為電網系統控制。

通信作者：? 于金鵬（1978-），男，山東乳山人，教授，博士生導師，泰山學者，主要研究方向為電能變換與電機系統控制。 Email： yjp1109@126.com