推土機液力變矩器數值分析及改進

（山推工程機械股份有限公司，山東 濟寧 272073）

液力變矩器是主要由泵輪、導輪和渦輪組成的傳動部件，以變矩器油等流體為能量傳遞介質，將機械能和流體動能之間相互轉化來傳遞動力。變矩器的葉輪是由空間扭曲葉片構成的，流體在葉輪流道內呈空間三維流動且復雜多變。隨工作狀態的變化，變矩器各個葉輪之間紊流流體相互耦合。由于流體的黏度特性，會引起二次流、脫流和旋渦等現象。這些因素都會使得研究變矩器性能變得復雜，無法準確地對其進行性能預測和改進。

隨著計算機技術的不斷進步，計算流體動力學（CFD）得到了長足的發展。它使用離散的數值計算方法和模擬實驗的方法進行研究、根據仿真結果進行優化和驗證，是比較有效且經濟合理的途徑。本文對推土機變矩器進行CFD 流場仿真研究獲取相關性能參數，并以此為基礎進行葉輪優化，再進行數值仿真性能預測和試驗測試對比驗證。

1 CFD建模及計算

CFD 數值模擬計算是一種很有效的研究變矩器葉輪內部流場和性能預測的研究手段。數值模擬可以對變矩器內部復雜的三維空間流動進行試驗，為改進設計以提供了有效快捷的工具。數值模擬與實驗研究相結合，提高了變矩器尤其是變矩器葉輪改進的設計質量、縮短研發周期。基于流體的質量守恒定律、動量守恒定律和能量守恒定律為基礎，采用有限體積法（FVM）離散方法和雷諾平均法中的兩方程k-ε模型紊流模型，對由液力變矩器的泵輪、渦輪和導輪組成的流道內的三維流場進行仿真計算，建模分析計算流程如圖1。

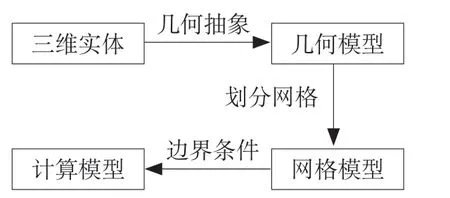
圖1 建模分析計算流程

以160hp 推土機的YJ380 系列變矩器為研究對象，在三維軟件Creo 中進行3 個葉輪的全流道三維建模。建模過程中的對物理模型進行簡化，忽略前后腔與密封環的間隙，模型如圖2。

使用IECM 對液力變矩器的整個流道模型進行網格劃分，并設定其邊界條件，最后導出液力變矩器全流道網格模型，如圖3 所示。

圖2 液力變矩器的幾何模型圖

圖3 全流道網格總裝配圖

將設置好的網格模型導入到CFD 軟件FLUENT 之后，設置計算模型求解器等項目參數。計算中采用三維瞬態流動模型，3D Time 選擇Unsteady；對于求解器solver 選擇Pressure Based Implicit 即基于壓力的非耦合隱式結構；Viscous Model 選擇兩方程模型k-ε紊流模型。Grid Interface 選項中設定泵輪出口面與渦輪入口面對接、渦輪出口面與導輪入口面對接、導輪出口面和泵輪入口面對接。為保證泵輪、渦輪、導輪三者接觸面（Interface 面）相互接觸并能有效模擬，一般情況下應設置計算模型之間的接觸面面積相同。迭代過程中須注意隨時按情況改變亞松弛因子以方便加快收斂，其他設置按默認狀態。

2 仿真計算和分析中的前提條件

油液介質在液力變矩器內部的流動十分復雜，有許多因素影響其流動。在流體計算中要忽略次要因素，研究主要因素，進行簡化模型。在CFD 軟件計算中一般做如下處理再進行計算。

1）計算模型中的流體假設為不可壓縮流體。

2）忽略溫度場和重力場對流體仿真的影響，僅研究流體的速度場和壓力場分布。

3）本文所研究的液力變矩器將所有構件認為是絕對剛體。

4）計算中忽略不計變矩器葉輪之間的流體泄漏量。

5）每個流道的流動規律為軸對稱分布。

6）流動的連續性。流體從上一個葉輪的流道流出后完全等量地流入下一個葉輪的流道內，即葉輪間的Interface 界面處流體流動的連續性。

7）忽略流體與壁面的圓盤摩擦損失等損耗，以半理想狀態流體進行仿真。

3 流場分析

液力變矩器在工作中是一個動態變化的過程。渦輪輸出軸受載荷的變化而變化，其轉速也會隨之自適應變化，整個變矩器內部流場是一個系統，泵輪的工作狀態也在變化。變矩器各性能參數與渦輪轉速之間的函數關系即為液力變矩器的外特性。一般情況下多采用泵輪、渦輪轉速比i作為橫軸繪制出變矩器外特性曲線。

為了更深入了解液力變矩器的工作原理和流場分布，以及研究內部流場的典型分布特性及其產生機理。這里選取轉速比i=0.78 的工況點，來研究分析變矩器的內部流場特性及性能參數。本文仿真中泵輪的轉速設置為恒定值2 000r/min，在此基礎上設置不同的渦輪轉速，計算多個轉速比的流場模型。通過對變矩器葉輪內流場參數的分布細致分析可以大致掌握液力變矩器內流體流動的狀態，并能進一步的對液力變矩器葉輪葉片優化做出指導。

分析數值模擬仿真結果得到的泵輪內部流道的壓力和速度分布場，可以得出泵輪出口壓力大于進口壓力，顯然這是由于泵輪的葉片對流道內流體做了功，提高了流體的能量，流體在流道壓力值逐漸升高。泵輪的葉片工作面的壓力值是大于葉片背面，是因為葉片工作面為壓力面、做功面，而葉片背面為吸力面、負壓面，這與泵輪內部流場規律的基本理論是一致的。葉片工作面速度卻小于葉片背面的速度，這是流體的環形速度（與泵輪旋轉方向相反，也稱為軸向漩渦速度）與流體相對速度（流道貫穿流動引起）疊加引起的，壓力面附近流體速度為流道內流體相對速度減去環形速度，背壓面附近流體速度為相對速度加上環形速度。可總結為泵輪內部的流動規律：壓力大的區域速度較低，壓力小的區域速度較大。

在轉速比i=0.78 時，泵輪流道內壓力場梯度、速度標量場的分布比較均勻，只有泵輪入口的極小局部區域，流體的壓力和速度存在劇烈的變化。泵輪流道入口葉片工作面處局部壓力場梯度突變大，而其葉片背面處局部壓力場出現負壓區域，泵輪葉片背面流體流動中產生一定的脫離，主要是由于壓力梯度大及旋轉速度導致的。

渦輪流道進口端面到出口端面的速度標量場變化較為均勻沒有突變。從渦輪流道的壓力梯度場可以得出：壓力梯度在流道內呈均勻過渡的帶狀分布，也沒有出現脫流和二次流動等影響流動效率的現象。流體流動穩定，速度場分布的比較均勻，渦輪的進口比出口速度大。隨著流體對葉輪的做功速度均勻的減少，速度梯度分布趨勢和壓力分布趨勢基本一致。

通過數值模擬仿真及分析，可以發現流道內的流體流動情況和定性分析的情況基本一致，這也保證了改型設計可以使用CFD 仿真結果作為改進優化的依據。根據全流道流場瞬態仿真結果和相關測試數據和資料，為提升變矩器的效率η和優化變矩器系數K，確定出導輪出口液流最優角，并以此進行其他葉輪改型設計。

4 改進優化及性能試驗

根據全流道流場瞬態仿真結果和相關測試數據和資料，為提升變矩器的效率η和優化變矩器系數K，確定出導輪葉片出口最優角，并以此為基礎進行其他葉輪改型設計。經過優化計算，導輪葉片出口角βD2為135°為最優角，變矩系數的優化區間為K∈[2.23，2.28]。在較為理想的工作條件下，經過綜合分析選取效率最大時變矩器各工作輪的角度數值。經過多次計算可以得到優化設計的部分結果如下。

變矩系數的優化區間K=2.27

泵輪葉片進口角βB1=46.67°

泵輪葉片出口角βB2=79.35°

渦輪輪葉片進口角βT1=129.23°

渦輪輪葉片出口角βT2=15.13°

導輪葉片進口角βD1=108.22°

導輪葉片出口角βD2=135°

為了進一步驗證優化方案的性能，對優化后的葉輪進行建模再進行CFD 內流場仿真及性能預測和試驗測試。被測試對象為優化后的YJ380 液力變矩器，其循環圓直徑為380mm。試驗中對動力均采用恒轉速，保持泵輪輸入轉速為1 500r/min，加載裝置設置多個轉速進行測試，最后將測試結果通過系數法換算到泵輪轉速為2 000r/min 時的狀態對應值。

根據模擬出的數據結果再由公式（1）計算得出相關的性能參數，并以此繪制出性能曲線。其中，橫軸為變矩器傳動比i從0 變化至1，縱軸為葉輪扭矩、效率η。液力變矩器外特性曲線，如圖4 所示。

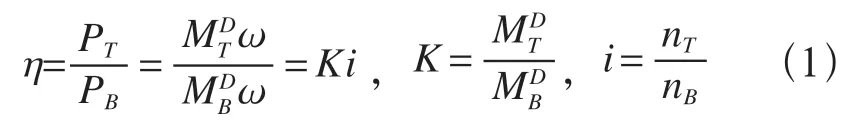
圖4 液力變矩器的外特性曲線圖

液力變矩器全流道的幾何模型數值仿真得出的泵輪力矩特性數值與實測值基本吻合相差不大，尤其是效率曲線變化趨勢基本吻合；而渦輪的數據相對于前兩者相差較為明顯。這是由于在三維建模和數值模擬中忽略了一些細節和外界條件的干擾，進而使流體處于較為理想的狀態以便計算較為容易收斂；泵輪的轉速是一定的，受外界影響相對小一些，而渦輪受負載和其他條件的影響較大。

對比實測數據與模擬數據以及外特性曲線圖，可以看出優化后的變矩器具有良好的效率性能表現，實測和仿真的變矩器最高效率分別達到82%和85%，兩者相差很小，說明數值性能預測是有效的。同樣，優化后的變矩器的效率高效區在速比0.5 ＜i＜0.86 之間，工作區域范圍更寬有更好的適用性。優化后的變矩器YJ380 裝機后性能符合主機要求，性能表現更佳。

5 結論

采用了三維瞬態流動的數值模擬仿真得出的液力變矩器內部流場分布和性能預測結果與實測參數是基本一致的，可以認為數值模擬是可信的，能夠較好地反映變矩器葉輪內部流體流動狀況，具有良好的參考價值和有效性。根據仿真試驗結果并進行葉輪優化，將CFD 軟件FLUENT 計算來代替液力變矩器的部分樣機試驗工作，具有較高的準確性和可靠性，為液力變矩器的設計、改進提供了一種便捷的方法，對于降低成本、縮短研發周期、提高研發效率具有實際意義。