非同量分數階永磁電機的混沌運動仿真

韓建群

摘 要：永磁電機工作在分數階狀態是一種更加普遍的電機工作情況，分數階永磁電機在特定環境下會出現混沌運行狀態，其混沌運行時存在運用整數階微分模塊進行分數階仿真困難的問題。本文針對非同量分數階永磁電機的混沌仿真問題，通過濾波器方法搭建了分數階永磁電機的仿真模型，并給出了分數階永磁電機混沌狀態運行相圖。仿真計算結果表明，該方法是有效的。

關鍵詞：非同量;分數階;永磁電機;混沌;仿真

中圖分類號：TM622文獻標識碼：A文章編號：1003-5168（2020）07-0037-04

Abstract： It is a more common case that the permanent magnet synchronous motor works in fractional order state. The fractional order permanent magnet synchronous motor can be chaotic in a specific environment. It is difficult to use integral order differential module for fractional order simulation in chaotic operation. In this paper， the simulation model of fractional permanent magnet synchronous motor was built by the filter method， and the phase diagram of fractional permanent magnet synchronous motor in chaotic state was given. The simulation results show that the method is effective.

Keywords： non-homogeneous;fractional order;permanent magnet synchronous motor;chaos;simulation

1 研究背景

永磁同步電機（Permanent-magnet Synchronous Motor，PMSM）是一種具有高可靠性、高效率和快速動態響應等優點的驅動設備，被廣泛應用于機器人、醫療設備、汽車電子等多種工程領域[1-3]。目前，關于分數階PMSM的研究漸成熱點。因為PMSM中廣泛存在的機械摩擦與沖擊、阻尼、齒隙動態等物理對象具有分數階特性[4-5]，實際電容和電感也具有分數階特性[4]，具有機械摩擦與沖擊、阻尼、齒隙動態以及電容、電感等儲能元件特性的電機也應該是具有分數階的，因此采用分數階微積分建立電機的數學模型能更加細膩地刻畫其動態行為，更為準確地描述其屬性特征[6]。

PMSM在工程中常常工作在額定轉速和轉矩狀態，從而保證電機的高效率。但是，在實際應用中，由于機械工作環境的變化，在特殊條件下，PMSM也呈現出混沌狀態，即電機的轉速和轉矩是間歇振蕩的，從而導致電機的控制性能不穩定，并且產生不規則的電磁噪聲[7]。從當前的研究結果可知，分數階PMSM系統會表現出混沌狀態。這促使人們利用分數階微積分理論更深入地研究混沌這一自然界普遍存在的物理現象，并探索分數階系統中的混沌控制與同步方法[8-9]。近年來，有學者利用分數階微積分建立了分數階PMSM系統模型，并通過穩定性理論分析、分數階系統的時域數值求解以及Lyapunov指數計算對系統混沌動力學特性進行研究，并給出了同量分數階PMSM系統出現混沌運動現象的最低階次及控制方法的有效性。

當采用MATLAB軟件對PMSM運行狀態進行仿真時，需要對整數階仿真模塊進行改進才能完成分數階PMSM系統狀態仿真。本文研究了不同量分數階PMSM混沌仿真方法，仿真結果驗證了該方法的有效性。

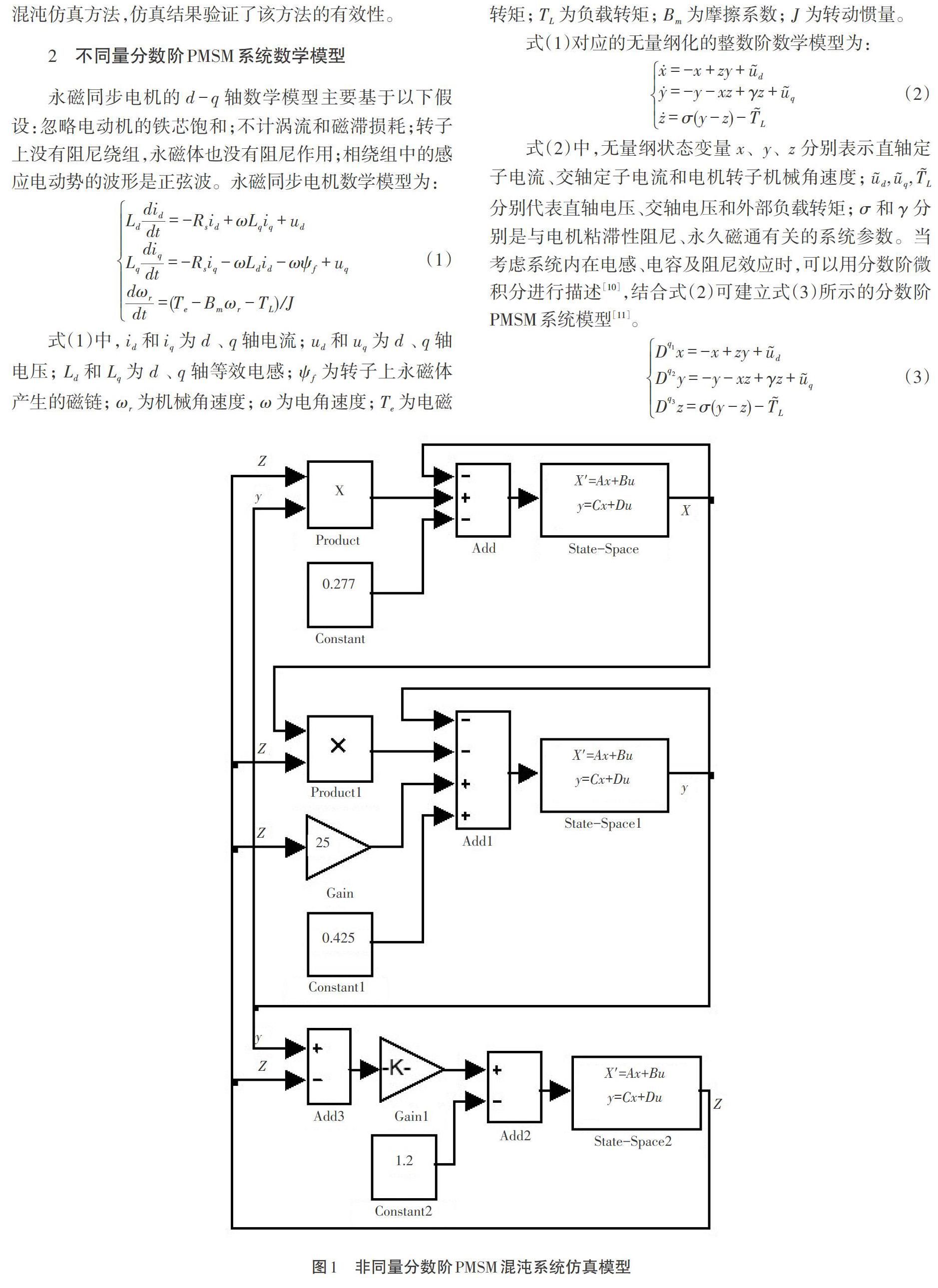
2 不同量分數階PMSM系統數學模型

4 結論

分數階PMSM是電機研究領域熱點之一。本文對非同量分數階PMSM系統進行介紹，研究了運用濾波器進行分數階仿真的方法，并運用分數階算子的State-space模塊建立了分數階PMSM仿真系統，并給出了分數階PMSM系統混沌運行的仿真結果。

參考文獻：

[1]Zheng P， Bai J ， Song Z， et al. Development of the compound-structure electrical machine and its key technologies for hybrid electric vehicles[J]. Journal of Harbin Institute of Technology，2016（3）：1-10.

[2]趙佳奇.永磁同步發電機無速度傳感器控制[J].控制工程，2016（11）：52-56.

[3] Miao L ， Zhang Y ， Tong C ， et al. Efficiency Optimization of Permanent Magnet Synchronous Generators Based on Model Predictive Direct Torque Control[J]. Diangong Jishu Xuebao/Transactions of China Electrotechnical Society，2018（15）：3535-3546.

[4]Faqiang W，Xikui M. Fractional order modeling and simulation analysis of Boost converter in continuous conduction mode operation[J]. Acta Physica Sinica，2011（7）：89-96.

[5] Barbosa R S ， Machado J A T . Describing Function Analysis of Systems with Impacts and Backlash[J]. Nonlinear Dynamics，2002（1-4）：235-250.

[6]趙遠征.分數階控制算法在永磁交流伺服系統中的研究與應用[D].南京：南京理工大學，2014.

[7] Chen J H ， Chau K T ， Chan C C . Chaos in voltage-mode controlled DC drive systems[J]. International Journal of Electronics，1999（7）：857-874.

[8] Matouk A E . Chaos， feedback control and synchronization of a fractional-order modified Autonomous Van der Pol-Duffing circuit[J]. Communications in Nonlinear Science and Numerical Simulation，2011（2）：975-986.

[9] Tavazoei M S ， Haeri M . Synchronization of chaotic fractional-order systems via active sliding mode controller[J]. Physica A： Statistical Mechanics and its Applications，2008（1）：57-70.

[10]陳文，孫洪廣，李希成，等.力學與工程問題分數階導數建模[M].北京：科學出版社，2010.

[11]Huang G Q ， Wu X .Analysis of Permanent-magnet Synchronous Motor Chaos System[C]//Lecture Notes in Computer Science， Artificial Intelligence and Computational Intelligence. Berilin：Springer.

[12]高遠，范健文，羅文廣，等.分數階永磁同步電機的混沌運動及其控制研究[J].武漢理工大學學報，2012（7）：134-140.