遞歸算法的應用與分析

倪錦園 張建勛

摘? 要：遞歸思想是算法分析設計中最重要的思想之一，遞歸算法應用十分廣泛，借助遞歸算法可以把一些較為復雜的問題簡潔地表示出來。該文重點介紹了遞歸算法的概念和三個特點，通過計算機博弈樹詳細說明了遞歸算法在數據結構中樹的應用，使用點格棋博弈過程落子的不同狀況系統地介紹了遞歸算法在圖的應用，并通過對照實驗重點分析了遞歸算法和遞歸算法非遞歸化的執行效率。

關鍵詞：遞歸;算法;非遞歸化;效率

中圖分類號：TP301.6? ? ? ? 文獻標識碼：A 文章編號：2096-4706（2020）20-0146-04

Application and Analysis of Recursive Algorithm

NI Jinyuan，ZHANG Jianxun

（College of Computer Science and Engineering，Chongqing University of Technology，Chongqing? 400054，China）

Abstract：Recursive thought is one of the most important thoughts in algorithm analysis and design. Recursive algorithms are widely used. With the help of recursive algorithms，some more complex problems can be expressed concisely. This article focuses on the concept and three characteristics of the recursive algorithm. This paper describes the application of recursive algorithm in data structure tree in detail through computer game tree，systematically introduces the application of recursive algorithm in graph by using different situations in the process of point chess game，and analyzes the execution efficiency of recursive algorithm and recursive algorithm non recursive through contrast experiments.

Keywords：recursion;algorithm;non-recursive;efficiency

0? 引? 言

在日常編程過程中，通過使用遞歸算法可以簡化大量的代碼，同時也讓代碼的可維護性變得更好。筆者通過將遞歸算法應用到點格棋博弈系統中，完成了整個博弈系統搜索引擎和測試引擎的實現，并在全國計算機博弈大賽上取得了較好的成績。遞歸算法是程序開發過程中一種重要的方法，通過遞歸算法可以讓程序的結構性更加清晰，可以把一些不容易解決的問題處理好，而且解題思路更為明確，不容易產生歧義。在算法分析與設計課程中很多問題都用到了遞歸的方法，比如漢諾塔問題、整數劃分問題、求階層問題等。遞歸算法的設計還是比較復雜的，要設計一個好的遞歸算法來解決以上問題就要注意三個關鍵點：首先分析問題的定義，找到合理的解決辦法就需要找出算法的遞歸公式，設計一個好的遞歸公式是解決問題的關鍵;其次設計一個遞歸的邊界條件也就是遞歸的終止條件是十分重要的;最后的關鍵是要不斷地縮小問題的規模，記錄遞歸時參數傳遞的過程[1，2]。

1? 遞歸算法概述

1.1? 遞歸算法概念

遞歸算法是指算法本身可以直接或者間接的調用自己，將一個較為復雜的問題分解為規模較小的子問題，算法在執行過程中重復不斷地實現自我調用的過程。在不斷遞歸調用的過程中，只有達到遞歸邊界的臨界值時，才會跳出遞歸循環，遞歸算法會從后往前依次逆序返回，就是把每一層遞歸調用的值放入一個棧中，算法執行到遞歸的出口時，就進行出棧的操作，從最后一層遞歸調用的值逆序返回，返回到第一個入棧操作，這樣就完成了整個遞歸算法的操作[3-5]。

1.2? 遞歸算法特點

遞歸算法在程序設計中是十分重要的方法，幫助解決了許多較為復雜的問題，遞歸算法極大地簡化了程序開發的工作量，使程序的結構性也較為清晰，可讀性更高，同時讓問題更容易被理解和接納。遞歸算法主要有下面三個特點。

1.2.1? 設計遞歸公式

遞歸算法直接或間接的調用自己本身，將一個較為復雜的問題化解為一個或多個子問題來求解，同時子問題與被分解的問題有同樣的算法，舉個簡單的例子遞歸求n個元素的和，可以寫出公式f（n）=n+f（n-1）進行遞歸迭代，還有比較經典的漢諾塔問題，就是以c柱為支撐柱，將a柱上n-1的盤子移動到b柱上的公式是f（n-1，a，c，b），移動的盤子打印輸出move（n，a，c）;以a柱為支撐柱，將b柱上的盤子移動到c柱的公式是f（n-1，b，a，c）。每一次迭代遞歸的時候，問題規模都在縮小，同時上一次的輸出成為了下一次迭代遞歸的輸入。

1.2.2? 遞歸算法的邊界條件

邊界條件就是遞歸的出口。遞歸算法不是無窮無盡的，當程序遞歸到最后一層時，就要返回輸出。由于每一層遞歸都會使問題規模不斷縮小，所以每一次遞歸都會越來越趨近于終止條件，直到達到終止的條件，返回臨界值。例如遞歸求階乘問題f（n）=n·f（n-1），遞歸的終止條件當n=1時，如果沒有遞歸的邊界條件，此時程序是無限循環的，沒有輸出結果。遞歸算法的邊界條件有的時候也不止一個，在整數劃分問題里面，要分別討論最大化分數值和被劃分的整數值大小關系，此時遞歸邊界條件也有多個的。

1.2.3? 縮小問題的規模

遞歸過程中需要不斷地減小問題地規模，而且遞歸算法是在直接或間接地調用自身，所以遞歸時參數傳遞的過程中，要逐步減少或者增加參數值向遞歸算法的邊界條件靠攏，控制了遞歸方向才能控制遞歸算法。例如斐波那契數，F（0）=

0，F（1）=1，F（n）=F（n-1）+F（n-2），每一次遞歸調用的過程中，問題的規模都在不斷地縮小，直到問題規模縮小到遞歸出口的時候，就達到了遞歸輸出的條件。

2? 遞歸算法的應用

2.1? 遞歸算法在樹中的應用

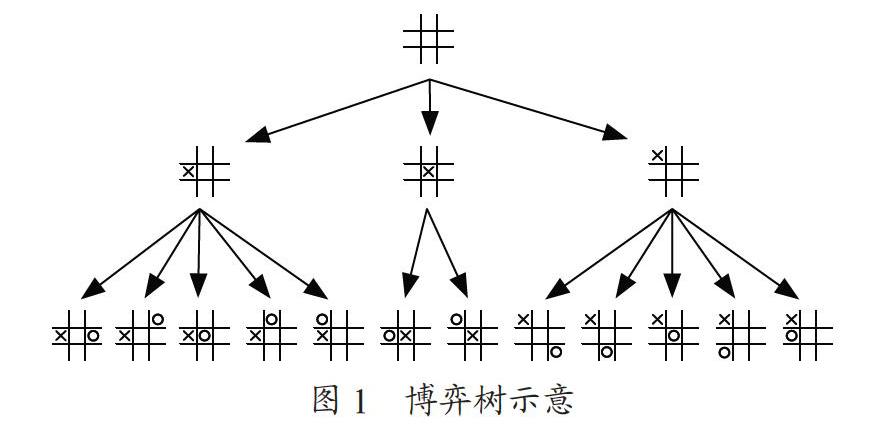
樹是一種基本的數據結構，它是由n（n>0）個有限節點組成一個具有層次關系的集合[6，7]。樹里面每一個節點具有相同的數據結構，每個數據元素直接的關系是“一對多”，所以很多有關樹的問題通常用到遞歸的思想。本文提到的計算機博弈樹也運用了遞歸的思想，博弈樹的每個節點代表一個落子后的一個局面，每個局面都是遞歸產生的，而且是通過深度優先遍歷，一層一層往下延伸，每一個局面生成的過程都會在上一層局面中進行遞歸搜索，搜索到上一層局面沒有落子的位置時，就會產生新的局面，它的根節點也就是現在所處的局面，也成為當前局面。因為雙方落子的不確定性，博弈樹的遞歸發展也是不一樣的，但總是根據棋盤信息進行模擬遞歸展開的，然后逐漸地就可以形成一個樹形結構。以井字棋為基礎的博弈樹的示意圖如圖1所示。在圖1中，博弈樹主要是通過井字棋來建立的，表現一局井字棋游戲博弈樹的全部過程，整顆博弈樹構建的過程是通過遞歸產生的，井字棋游戲是由雙方輪流著邊的棋類博弈游戲。

在圖1中的根節點表示一個空棋盤，根節點下面的三個子節點中的×表示一號玩家可以走的位置，在接下面的一層節點中的○表示的是二號玩家可以走的位置，二號玩家的落子位置完全要根據一號玩家的落子位置，通過遞歸搜索確定此位置未被一號玩家占領后，才能產生，因此，在棋局的不斷進行中，博弈樹在每一層遞歸的過程中也會越來越大。

2.2? 遞歸算法在圖中的應用

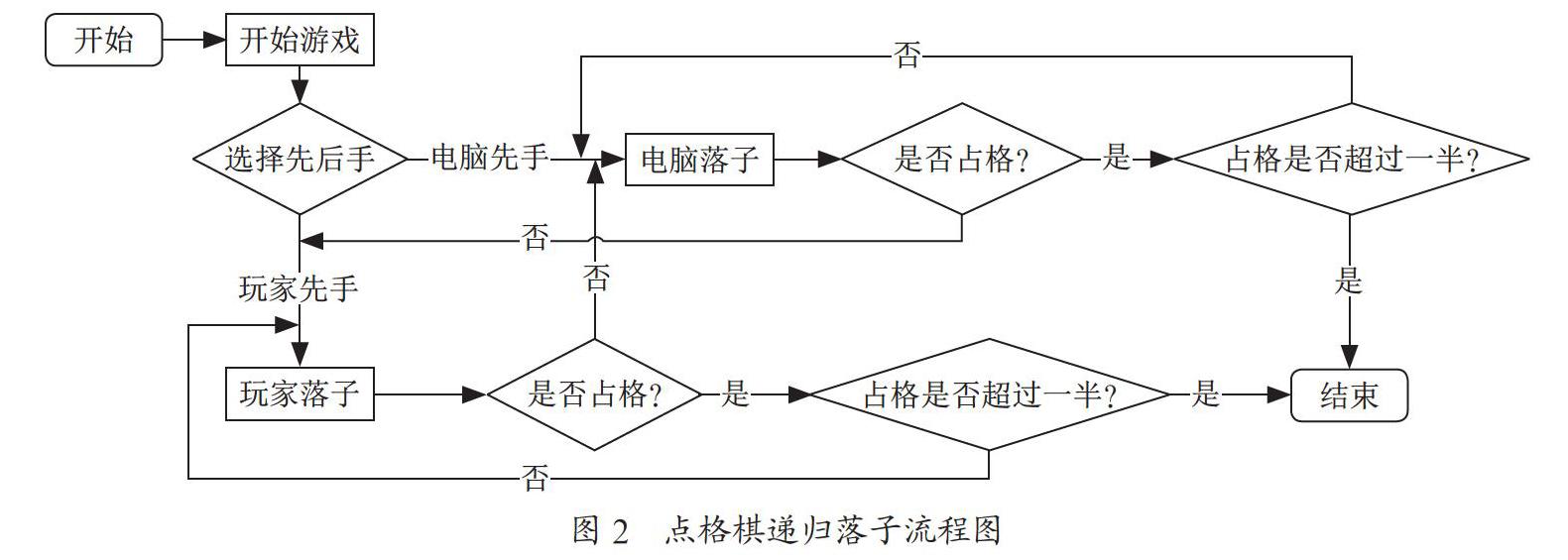
遞歸算法在圖中的應用是用來描述點格棋先后落子位置順序的算法，圖是由頂點V集和邊E集構成，因此圖可以表示成G=（V，E），圖是一種基本的數據結構，在很多有關于圖的應用中都用到了遞歸算法。點格棋博弈的過程中用到了有關于圖的遞歸算法，點格棋是中國計算機博弈大賽的競賽項目之一，博弈雙方輪流將兩個相鄰的點連接成一條邊，邊屬于雙方共有，只討論格子的所屬，當某一個格子的四條邊都被連成線時，占領最后一條邊的玩家擁有這個格子，占領格子后有一個獎勵邊，該玩家必須再下一步。根據這個競賽規則，可以用遞歸算法的思想來設計點格棋博弈雙方落子的流程圖，點格棋遞歸落子流程圖如圖2所示。

博弈雙方在落子的過程中選擇先后手遞歸進行落子，若電腦先手，電腦進行落子，然后條件判斷當前落子是否達到占格的條件，若沒有占格，則由玩家進行落子，若都沒有達到占格的條件，就遞歸到另一方進行落子。若任意一方達到占格的條件，則判斷當前占格數量是否超過所有格子的一半，若超過一半就跳出循環，若未超過一半就又遞歸調用自身落子的函數，在點格棋雙方博弈的過程中，不斷地遞歸調用落子的函數。

3? 遞歸算法與非遞歸化

對比遞歸算法和遞歸算法的非遞歸化時，下面就實際操作一個案例來分析各自執行效率，完成任務問題：在一個雙線程的電腦上，有n個任務將要完成，完成一個任務都將占用一個線程。一個線程完成任務的方法有兩種，可以一次完成一個任務，也可以一次完成兩個任務。需要完成n個任務，一共有多少種執行的方法。

用遞歸思想的具體思路：

（1）當只有一個任務的時候，有一種完成任務的方法。

（2）當只有兩個任務的時候，有四種完成任務的方法：分別是兩個任務分別占用兩個不同的線程，有兩種;一個線程一次性完成兩個任務，有兩種。

完成任務問題的算法實現包括了遞歸算法和非遞歸算法。

3.1? 遞歸算法

遞歸算法在程序執行的過程中，不斷地直接或間接的進行自我的調用，遞歸調用的過程中，系統會為每一層調用開辟新的棧來存儲信息，直到程序執行到邊界條件的時候，才完成自我調用，然后逆序返回棧中每一層存儲的數據，直到把棧里面的數據全部返回，到此就完成了整個遞歸算法的執行。在解決很多問題的時候，遞歸算法是十分有效的，它對問題的描述清楚易懂，便于對整個程序的編寫和調試。但是遞歸的過程中需要用到系統的堆棧，會消耗更多的空間資源，當遞歸深度過于龐大的時候，程序有可能會出現異常死機的現象[8]。完成任務問題的遞歸算法代碼為：

#include

#include

#include

int Digui（int n）

{

if（n==1）? ? ? ? //只有一個任務時，有一種方法

return 1;

if（n==2）

return 4;? ?//有兩個任務時，有四種方法

return Digui（n - 1）+Digui（n - 2）;

}

int main（）

{

long int begin，end;

time（&begin）;

int n;

printf（"請輸入任務量：＼n"）;

scanf（"%d"，&n）;

printf（"任務完成的方法一共有：＼n"）;

printf（"%d＼n"， Digui（n））;

time（&end）;

printf（"程序執行過程中的時間：＼n"）;

printf（"%d＼n"，end-begin）;

return 0;

}

3.2? 非遞歸算法

非遞歸算法執行效率更高，運行時間會隨著程序循環的次數增加而增加，沒有其他額外調用的開銷，非遞歸算法比遞歸方法更快，因為非遞歸方法避免了一些列函數調用和返回中涉及的額外開銷，在性能上更具有優勢[9，10]。完成任務問題的非遞歸算法代碼為：

#include

#include

#include

int main（）

{

long int begin，end;

time（&begin）;

int x1=1，x2=4;

int n，x;

printf（"請輸入任務量：＼n"）;

scanf（"%d＼n"，&n）;

for（int i=3;i<=n;i++）

{

x=x1+x2;

x1=x2;

x2=x;

}

printf（"任務完成的方法一共有：＼n"）;

printf（"%d＼n"，x）;

time（&end）;

printf（"程序執行過程中的時間：＼n"）;

printf（"%d＼n"，end-begin）;

return 0;

}

對照兩個實驗可以發現：遞歸算法程序結構簡單，易讀性更高，程序調試也很方便，但是遞歸算法依靠棧來實現操作的，不斷地在系統內部進出棧，占用了大量的時間和空間，消耗了更多的計算機資源，上述遞歸算法的時間復雜度O（2n），其中n代表問題的規模。而非遞歸算法程序結構較為復雜，在編寫和調試程序時，會花更多的時間，但因為非遞歸算法依賴于調用其他函數進行進出棧操作，相對于遞歸算法來說，消耗了較少的時間和空間。上述非遞歸算法的時間復雜度O（n）。

當輸入任務量為20時，遞歸算法程序執行時間不到1秒，非遞歸算法程序執行時間也不到1秒，由此看來，任務量較小的時候，遞歸算法和非遞歸算法執行的時間幾乎相同。當輸入的任務量為40時，遞歸算法程序執行時間為6秒，非遞歸算法程序執行時間只有2秒，當任務量較大的時候，遞歸算法明顯比非遞歸算法更慢。

4? 結? 論

全文對遞歸算法進行分析，通過對遞歸算法的概念和特點進行闡述，然后分別介紹了遞歸算法在樹、圖中的應用，接著做了遞歸算法和非遞歸算法的對照實驗，發現當數據量不夠大時，遞歸算法和非遞歸算法的時間效率幾乎相同，當數據量越來越大時，遞歸算法的執行時間相比非遞歸算法來說就越來越慢，遞歸算法的時間復雜度也要大于非遞歸算法的時間復雜度，所以遞歸算法的執行效率更低。因此在實際計算中，還是建議不要大規模使用遞歸算法。

參考文獻：

[1] 宋衛紅.數據結構中遞歸算法的教學研究 [J].現代信息科技，2020，4（13）：188-190+193.

[2] 張耀民.遞歸算法在程序設計中的應用與分析 [J].電子測試，2013（13）：1-2.

[3] 楊嬌.遞歸思想及其算法設計的探討 [J].數字通信世界，2018（11）：109+204.

[4] 晏素芹.遞歸算法的教學方法探討——以C程序設計為例 [J].福建電腦，2018，34（8）：170-171.

[5] 周世杰.從計算思維的視角辨析算法中的遞歸與迭代 [J].中國信息技術教育，2020（9）：53-55.

[6] 劉曉靜.“數據結構與算法”課程教學改革與實踐 [J].微型電腦應用，2015，31（11）：14-17+2.

[7] 張安勤，田秀霞，張挺.數據驅動的數據結構課程案例設計研究與實踐 [J].軟件工程，2020，23（4）：54-56.

[8] 王愛法，楊梅梅，福春霞.二叉樹及其遍歷算法的應用 [J].重慶理工大學學報（自然科學），2018，32（11）：194-198.

[9] 肖紅德.漢諾塔問題遞歸算法與非遞歸算法比較 [J].軟件導刊，2018，17（8）：118-120.

[10] 詹澤梅.數據結構中遍歷操作的非遞歸算法 [J].電腦知識與技術，2017，13（28）：40-42.

作者簡介：倪錦園（1996—），男，漢族，重慶九龍坡人，碩士，研究方向：數字圖像處理與分析;張建勛（1971—），男，漢族，四川樂山人，教授，碩士生導師，CCF專業會員，博士，研究方向：數字圖像處理與分析、實時計算機圖形學。