艦船用配電柜散熱分析

趙克威, 徐 敏

(中國船舶電站設備有限公司，上海 200129)

0 引 言

隨著綜合電力推進技術和造船技術的飛速發展，船舶自動化、電氣化水平越來越高。艦船對電力的需求呈幾何級數增長，其電力系統由過去的輔助系統變為主要系統。

電器屏柜是艦船電力系統的重要組成，集中了大部分的低壓電器設備和控制設備。電器屏柜是電器設備和控制設備的電氣性能得以實現的重要保障[1]。柜內元器件功率高，有效散熱面積小，導致單位面積發熱量升高，這種熱驅動引起的機械、化學、電氣等方面的問題可能嚴重影響元器件的質量和可靠性[2]。散熱情況的好壞還會影響操作人員的熱舒適性，關系到任務的執行效率[3]。因此，需對電器屏柜內功率元器件的散熱問題進行研究，以保證系統的整體功效，避免工程實施后出現較大問題。

電器屏柜通常設計成封閉的系統，這種形式使屏柜只能采用外部自然冷卻的散熱形式，而柜內元器件所釋放的熱量全部由殼體吸收[4]。配電柜是電器屏柜的一種，內部斷路器和銅排導電發熱，熱量通過對流、輻射、擴散等3種方式傳到外部空間[5]。箱內空間狹小，不易散熱，需優化配電柜內部結構、表面通風孔隙幾何形狀及位置，保證配電柜內部溫度分布滿足相關規范。

電子機柜散熱的計算方法包括基于傳熱實驗關聯式的解析計算方法和基于計算傳熱學的數值計算方法。張云超[6]采用解析計算方法對某艦船用電子設備開式機柜進行散熱設計。戰乃巖等[7]以小型電子設備散熱技術為背景，運用具有QUICK差分格式的SIMPLE算法，借助Fortran語言，對小空間熱源群繞體自然對流進行三維仿真模擬。陳文博[8]通過搭建精確下送風模型實驗臺，并結合CFD數值模擬研究單機柜通風和溫度問題。徐燕飛[9]對電器設備中主要元器件進行通風散熱數值分析和試驗研究，建立一套電子元器件熱分析和熱改進方法。

根據配電柜的設計方案，使用Fluent軟件進行計算，分析配電柜溫度分布狀況，并根據分析結果對配電柜的結構進行優化設計，使配電柜整體滿足相關規范的要求。

1 配電柜的建模及計算

1.1 計算傳熱學

通過換熱原理分析，可將配電柜散熱問題歸結為求解流體動力學方程組的問題。其基本方程為流體力學中的質量、動量和能量守恒方程。

連續性方程：

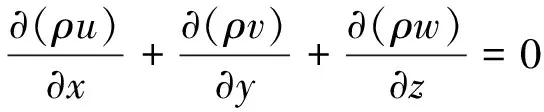
(1)

動量方程：

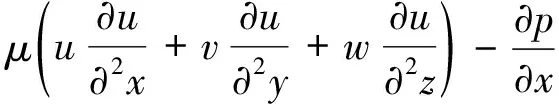
(2)

(3)

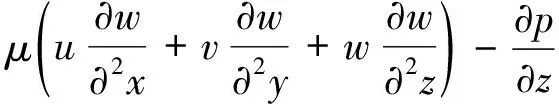
(4)

能量方程：

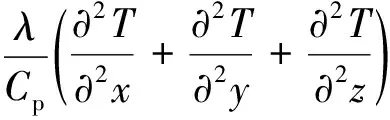
(5)

式(1)～式(5)中：ρ為流體密度，kg/m3；u、v、w分別為流體在x方向、y方向及z方向的速度分量，m/s；μ為流體的黏性系數，kg/(m·s)；p為流體內部壓力，Pa；g為重力加速度，m/s2；T為流體溫度，℃；Cp為流體的比熱容，J/(kg·K)；λ為流體的導熱系數，W/(m·K)。

但是，與常規的流體力學問題不同，若干與傳熱相關的影響因子也需要被考慮到：

(1) 選擇湍流模型。流場為湍流狀態，需采用雷諾平均方程與脈動方程相結合的算法。由于脈動方程為經驗或半經驗公式，不同湍流的脈動方程有其自身的適用范圍，所以需考察湍流模型對計算結果的影響，選用合適的湍流模型才能得到合理的計算結果。研究選用工程流體計算中最常用的標準k-ε湍流模型。

(2) 邊界處理方法。由于邊界層內的流動狀態對傳熱效果影響很大，所以在數值計算時需注意邊界層網格設計及邊界層模型對計算結果的影響。在網格設計方面，由于配電柜內部結構非常復雜，所以采用結構化網格進行網格劃分。在邊界層模型方面，采用工程流體計算中最常用的標準壁面函數模型。

(3) 氣體壓縮性。如果采用不可壓氣體，將無法產生浮力，無法計算自然對流問題。根據溫度和壓力的變化范圍可知，研究對象適用完全氣體模型，氣體狀態方程采用克拉伯龍方程。

(4) 氣體浮力和重力作用。在控制方程中引入重力和浮力項。

(5) 固體壁面間輻射換熱。需要估計固體表面熱輻射參數，數值計算時在能量方程中引入輻射熱。在仿真計算中采用Fluent提供的S2S模型處理輻射換熱。

1.2 計算參數設置及網格劃分

根據配電柜的設計圖紙和三維模型，對其有限元模型進行簡化，省略螺釘和倒圓角等對計算影響較小的零部件。全計算域幾何模型如圖1所示，內部為配電柜，最外層方框為艙室邊界。配電柜內部幾何形狀及外表面如圖2和圖3所示。

在進行傳熱計算時，配電柜內各部件精確的熱力學參數設置如下：

(1) 銅排總發熱量為2 000 W，斷路器發熱量為653 W；

(2) 銅排的材料屬性為銅，其他結構材料屬性為鋼；

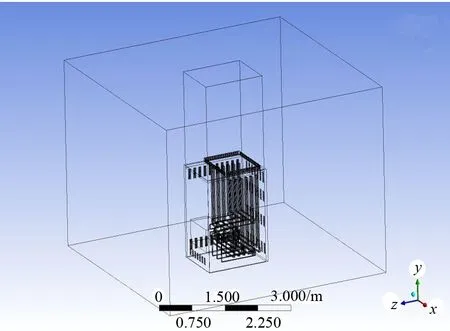
圖1 全計算域幾何模型

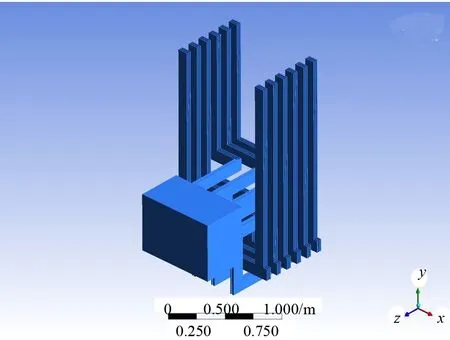
圖2 配電柜內部斷路器和母排形狀

圖3 配電柜外表面

(3) 固體表面發射率取0.8。

在計算時采用非結構網格，雖然操作簡便，但是網格數量大幅上升，內存溢出，計算時間大幅增加，計算誤差難以控制。結構化計算網格操作稍復雜，但計算速度快，誤差相對可控，所以模型網格劃分采用結構化網格。配電柜內網格分辨率為5 ～10 mm，網格總量約1 200萬個。銅排和斷路器表面網格細節如圖4所示。

圖4 銅排和斷路器表面網格

1.3 邊界條件設定

環境溫度為50 ℃，艙室邊界、配電柜及內部各部件表面為固壁邊界條件。位于計算域最外層的艙室邊界溫度固定為323 K。內部各部件表面溫度通過計算得出。通過這樣的設計使得數值計算模型中的邊界條件、邊界與內部輻射換熱模式、環境溫度對計算域內部的影響等與實際情況保持一致。為了方便計算研究，給配電柜內部的銅排進行編號。圖5為各銅排編號情況。

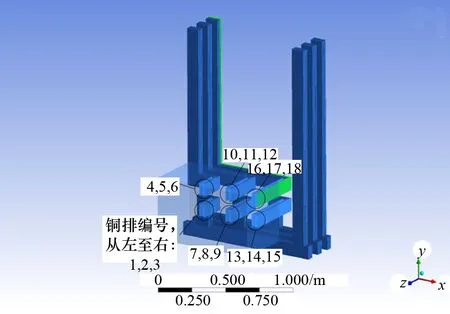
圖5 銅排編號

由于每根銅排的電阻和電流各不相同，其發熱量也不相同。在銅排總熱量為2 000 W的前提下，可根據每根銅排的長度、電阻和電流計算各自的焦耳熱與總熱量之比，從而求得每根銅排表面熱流密度。表1為各銅排表面熱流密度。

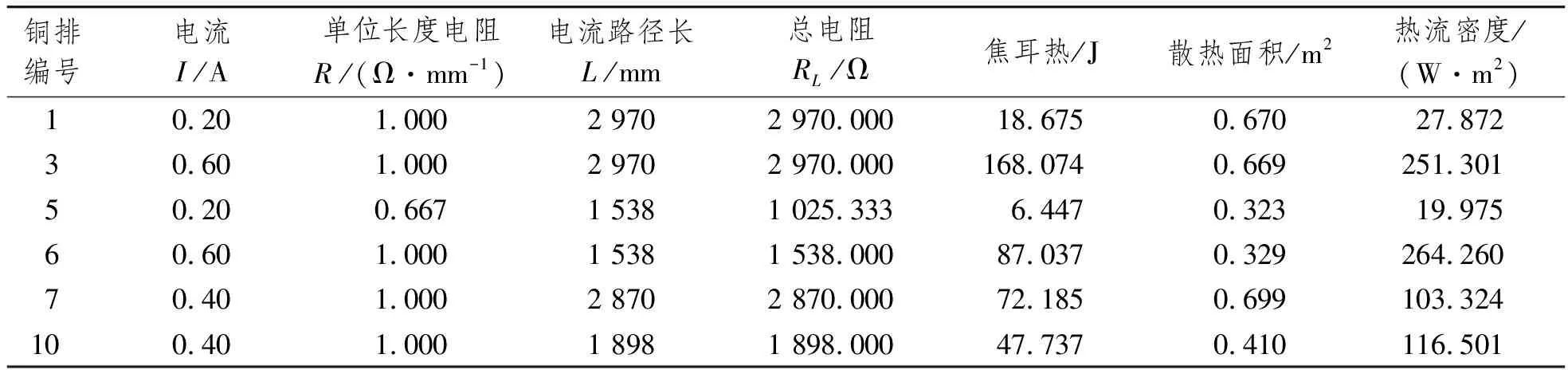
表1 典型銅排表面熱流密度

2 計算結果與分析

(1) 自然對流現象

配電柜內氣體流速分布如圖6所示。配電柜內部銅排和斷路器工作時不斷發熱，對氣體加熱，被加熱的氣體密度降低，向上運動，最大運動速度約0.65 m/s。

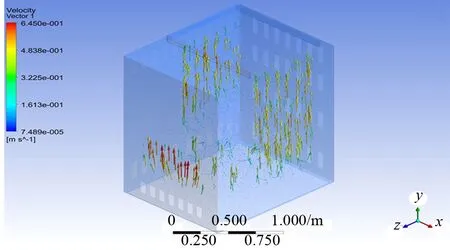
圖6 配電柜箱內氣體速度分布狀況

(2) 斷路器、銅排及箱體表面溫度狀況

應用有三個方面：一利用模型對其他未知化合物的相關性質/活性進行預測，在效應評價和暴露評價等方面可彌補缺失的數據，對有機化合物進行篩選和評價；二根據模型的組成與形式，結合已有的化學、生物學知識，探求有機化合物的毒理性質、環境過程和生態效應等機理分析；三根據所闡明的結構-性質關系結果，為設計目標化合物指明方向。

斷路器、銅排及箱體表面溫度狀況如圖7～圖9所示。

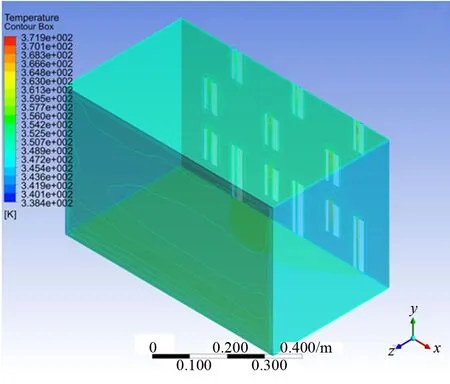
圖7 斷路器表面溫度分布

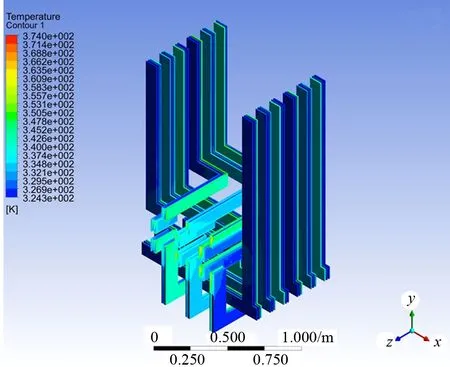
圖8 銅排表面溫度分布

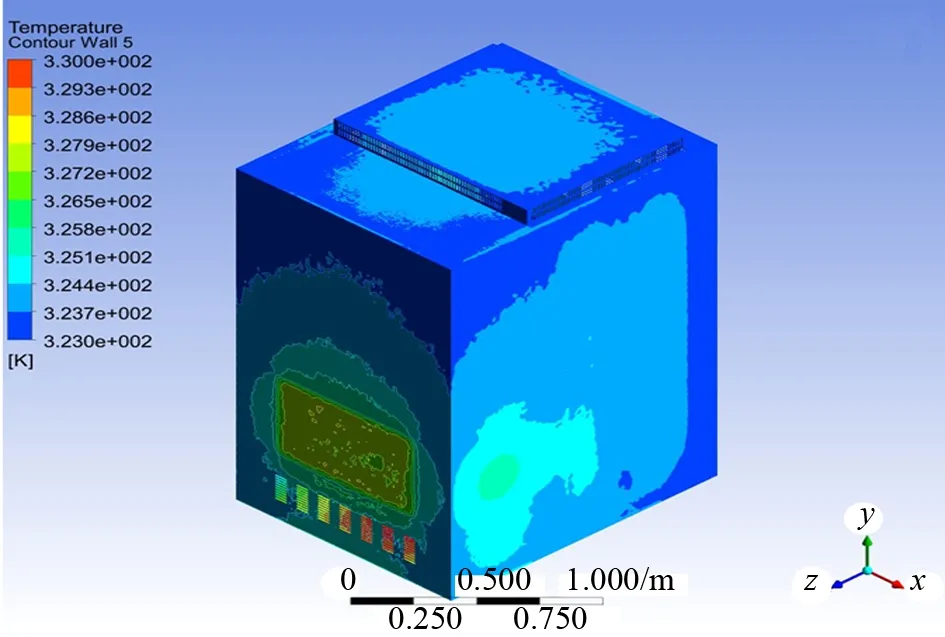
圖9 箱體表面溫度分布

由計算結果可以看出，全流域溫度分布范圍為323～374 K。斷路器發熱量為653 W，平均表面熱流密度為358 W/m2；表面溫度范圍為338～372 K，表面平均溫度為349 K。銅排發熱量為2 000 W，平均表面熱流密度為95 W/m2；表面溫度范圍為324～374 K，表面平均溫度為333 K。箱體表面溫度范圍為323～330 K，表面平均溫度為325 K。

雖然斷路器發熱量較低，但是其表面平均熱流密度更高，所以斷路器表面平均溫度高于銅排表面平均溫度。斷路器和銅排的平均溫度與最低溫度接近，說明斷路器和銅排表面大部分區域溫度并不高，斷路器表面平均溫度比環境溫度高約26 ℃；銅排表面平均溫度比環境溫度高約10 ℃。但是，箱內結構復雜，局部位置氣流不暢，無法有效散熱，因而斷路器和銅排表面局部區域產生熱斑。

(3) 高溫區域

圖10和圖11為銅排和斷路器高溫熱斑位置。

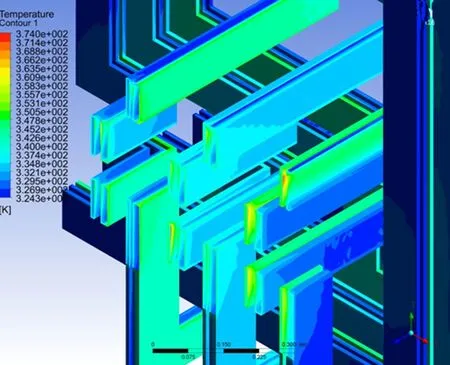
圖10 銅排熱斑位置

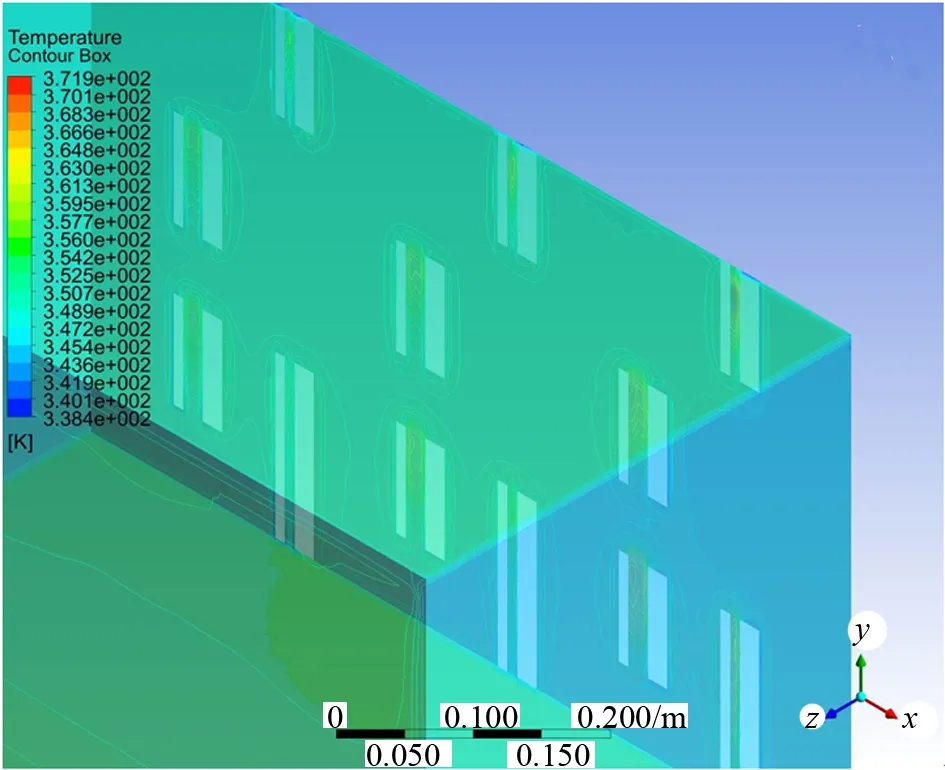
圖11 斷路器熱斑位置

3 試驗測試

試驗根據GJB 150.4A-2009的要求進行，試驗中主母線周圍空氣溫度為50 ℃，部分測試點試驗結果與計算結果的比較如表2所示。

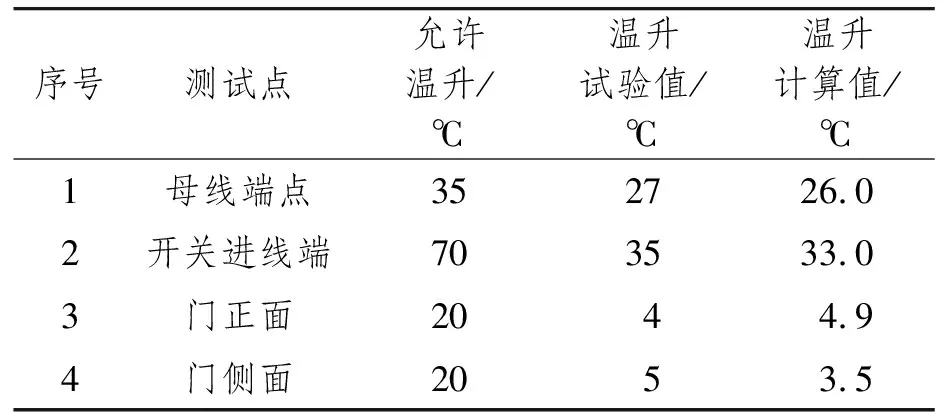
表2 部分測試點試驗結果與計算結果比較

由表2可以看出，計算結果與試驗結果基本一致。

4 結 語

通過對低壓配電柜的散熱計算分析可以看出，低壓配電柜的平均溫度不算太高，但是由于散熱效果不良產生的熱斑會造成局部高溫。因此，配電柜散熱的關鍵在于降低熱斑溫度。在進行配電柜設計時，應該減少結構復雜度，拓寬縫隙，必要時加入通風設備，在最高溫區形成對流。