線電荷與帶有低脊的接地導體薄圓筒所形成的電場及其數值模擬（上）

王福謙

（西南交通大學希望學院，成都610400）

0 引 言

文獻［1-8］中分別運用鏡像法和保角變換分析了接地薄圓筒內線電荷的電場，而線電荷與帶有低脊的接地導體薄圓筒所形成的電場的研究，相關文獻還未見報道。為此，本文擬通過保角變換討論線電荷與帶有低脊的接地導體薄圓筒所形成的電場，給出其電勢分布函數，并利用數學軟件Matlab對場分布進行數值模擬，繪制出電場線和等勢線（面）圖。

1 電勢分布

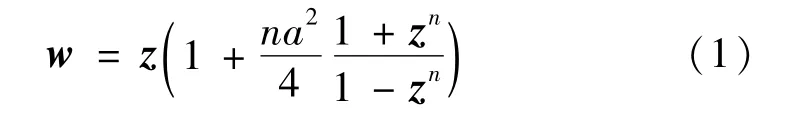
圖1 帶有低脊的薄圓筒與線電荷的橫截面

圖2 變換后的薄圓筒與線電荷的橫截面

為計算簡便計，本文具體計算線電荷與帶有一條低脊接地導體薄圓筒所形成的電場（圖略），即低脊的數目n＝1，與此相應的變換函數式（1）可寫為：

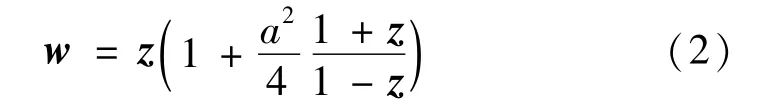
上式將z平面上線電荷的位置的z0＝x0＋jy0，變換為w平面上的w0位置，該位置由式（2）給出：

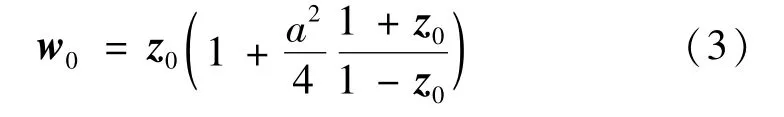
再作將單位圓變換為單位圓并把荷電線所在位置變換在圓心的分式線性變換［10］

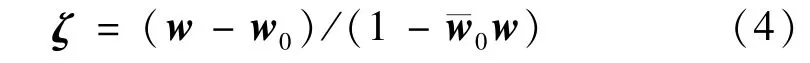
經此變換后，帶有一條低脊接地導體薄圓筒的橫截面在ζ平面上的形狀映射為圓形，且荷電線位于圓心上，如圖3所示。

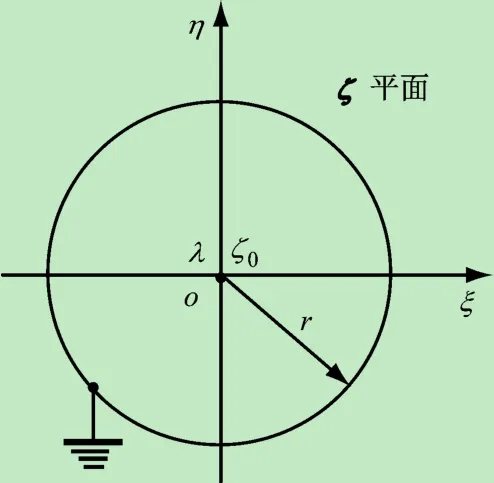
圖3 再變換后的薄圓筒與線電荷的橫截面

對與圖3對應的無限長的圓柱形區域，電場的分布具有軸對稱性，而在ζ平面上r＝1的圓周上各點的電勢均為零（因在z平面上圓筒接地）。由此可得該區域內的電勢分布為：

式中，r為觀察點到ζ平面原點的距離。由ln（ρeiφ）＝ln ρ＋ iφ 知，ln＝ln r，則可知ζ 平面上靜電場的復勢為：

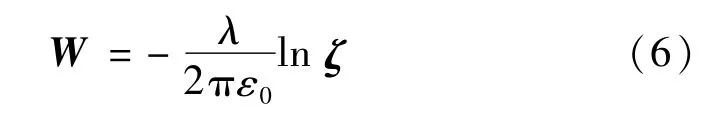
設復函數z＝x＋iy，則ζ（z）＝ ξ（x，y）＋ iη（x，y），由式（2）、（3）得

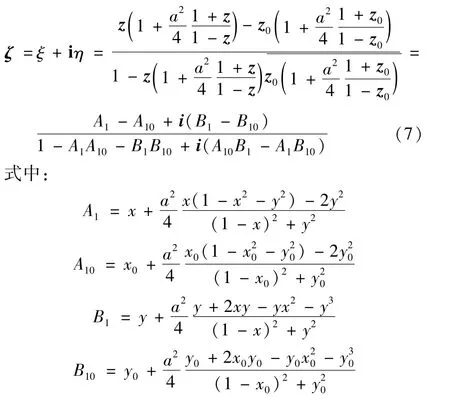
由式（7），該靜電場的復勢式（6）可表示為：

式（9）為線電荷與帶有一條低脊的接地導體薄圓筒所形成電場的電勢分布解析式。

2 場分布的數值模擬

為了給出線電荷與帶有一條或多條低脊的接地薄圓筒導體所形成電場的電場分布直觀圖像，并檢驗本文研究結果的正確性，下面通過式（1）、（3）及（8），利用數學軟件Matlab［12-16］繪制出的線電荷與帶有低脊的接地薄圓筒導體所形成電場的電場線等勢線（面）圖。

圖4～7為接地導體薄圓筒內低脊的數目分別為1、3、4和5時，線電荷與帶有低脊的接地薄導體圓筒所形成的電場的電場線等勢線（面）圖。由圖可見，圓筒內表面上的低脊的數目越多，高度越大，對電場的影響越大；電場線垂直于導體表面和等勢線；以上的場線分布特征均科學合理［12］，為預期結果，這說明本文的研究方法正確，結論可靠。應該注意的是，變換函數式（1）僅適用于低脊的間距較大且其高度很小的情形，當低脊的數目過多，以至于相鄰低脊間的距離很小，或低脊的高度較大時，均不能應用本文給出的方法進行研究，也即，本文的研究方法僅適合于低脊的間距較大且高度很小的情形。特別的是，當低脊消失時，其內部的電場分布又回到線電荷與接地薄圓筒所形成電場的情形［3］（見圖8）。

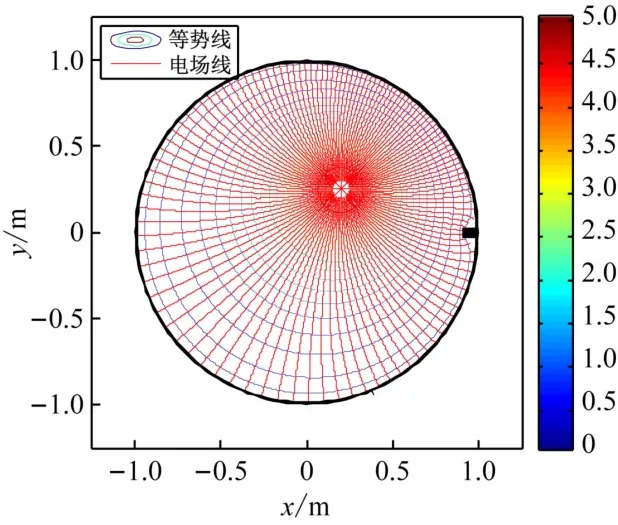
圖4 線電荷與帶有低脊的接地薄導體圓筒所形成的電場（λ＝2.6 C／m，x0＝0.2 m，y0＝0.5 m，a ＝0.1 m）

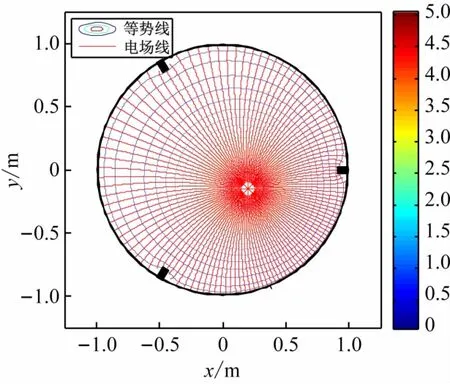
圖5 線電荷與帶有低脊的接地薄導體圓筒所形成的電場（λ＝2.5 C／m，x0＝0.2 m，y0＝ -0.15 m，a＝0.1 m）

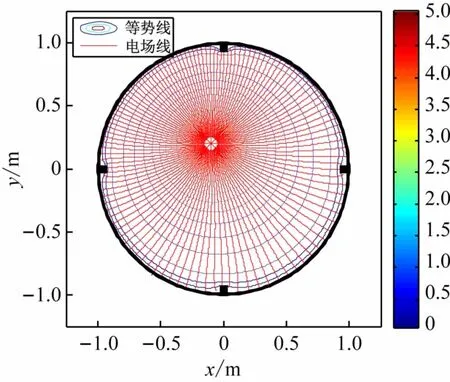
圖6 線電荷與帶有低脊的接地薄導體圓筒所形成的電場（λ ＝ 1.5 C／m，x0＝ -0.1 m，y0＝0.2 m，a＝0.08 m）

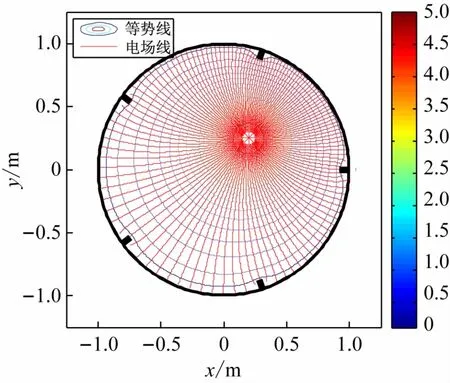
圖7 線電荷與帶有低脊的接地薄導體圓筒所形成的電場（λ ＝2.5 C／m，x0＝0.2 m，y0＝0.25 m，a＝0.085 m）

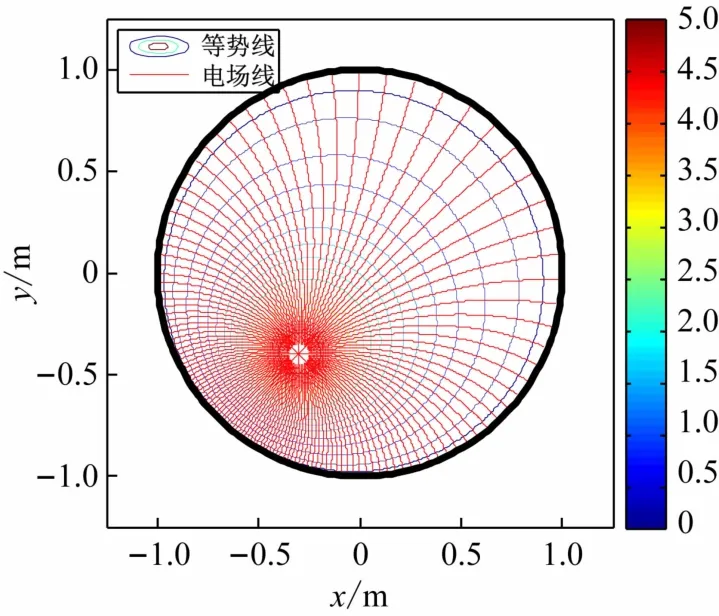
圖8 線電荷與帶有低脊的接地薄導體圓筒所形成的電場（λ ＝2.5 C／m，x0＝ -0.3 m，y0＝ -0.4 m，a ＝0）

3 結 語

本文將理論分析與計算機數值模擬相結合，研究了線電荷與帶有低脊的接地薄導體圓筒所形成的電場，給出其電勢及場強分布的解析解，并利用Matlab軟件對其進行數值模擬，實現了場分布的可視化，為邊界復雜的靜電場邊值問題的求解提供了一種思路與方法，可供電線電纜中相關問題的研究借鑒和參考。