含有Dzyaloshinskii-Moriya相互作用的自旋1鍵交替海森伯模型的量子相變和拓撲序標度*

陳愛民 劉東昌 段佳 王洪雷 相春環 蘇耀恒

1) (西安工程大學理學院, 西安 710048)

2) (重慶醫科大學醫學信息學院, 重慶 400016)

3) (重慶醫科大學公共衛生與管理學院, 重慶 400016)

利用張量網絡表示的無限矩陣乘積態算法研究了含有Dzyaloshinskii-Moriya (DM)相互作用的鍵交替海森伯模型的量子相變和臨界標度行為.基于矩陣乘積態的基態波函數計算了系統的量子糾纏熵及非局域拓撲序.數據表明, 隨著鍵交替強度變化, 系統從拓撲有序的Haldane相轉變為局域有序的二聚化相.同時DM相互作用抑制了系統的二聚化, 并最終打破系統的完全二聚化.另外, 通過對相變點附近二聚化序的一階導數和長程弦序的數值擬合, 分別得到了此模型相變的特征臨界指數a和b的值.結果表明, 隨著DM相互作用強度的增強, a逐漸減小, 同時b逐漸增大.DM相互作用強度影響著此模型的臨界行為.針對此模型的臨界性質的研究, 揭示了量子自旋相互作用的彼此競爭機制, 對今后研究含有DM相互作用的自旋多體系統中拓撲量子相變臨界行為提供一定的借鑒與參考.

1 引 言

在多體系統中, 量子相變是由量子漲落占主導地位而引起的一種量子效應, 近年來一直是凝聚態物理中的研究熱點[1?4].在量子相變中, 系統的基態會發生劇烈的變化, 其關聯長度在臨界點處是發散的, 且激發能譜的能隙消失.一般情況下, 局域序的產生伴隨著系統的自發性對稱破缺, 被稱為Landau-Ginzburg-Wilson范式.對此類相變的刻畫, 一般采用量子糾纏[5]、量子 concurrence[6]、保真度[7]等方法.在相變點附近, 量子糾纏、比熱及磁化強度等物理量按照特定的函數關系發散, 呈現確定的標度行為.除此之外, 自然界中還存在著一類不能夠用Landau-Ginzburg-Wilson范式的對稱破缺描述的拓撲類量子相變, 此類相變不存在描述區分相變的局域序參量, 呈現無序或長程拓撲序,例如自旋拓撲有序的Haldane相[8].

在低維多體系統中發現的含有拓撲相變的新物質態極大地豐富了我們對自然界的認知.然而,受到研究方法的限制, 長程拓撲序及其標度行為一直是低維系統中量子相變研究的難題[9].近年來發展的張量網絡表示算法被證明對低維無限格點系統中非局域的長程序刻畫是非常成功的[10].此方法恰好為我們研究拓撲類量子相變的標度行為提供了強有力手段.

為了探究低維自旋系統中具有非局域序的拓撲量子相變及物理效應對相變的影響, 本文選取了自旋 1的含有 Dzyaloshinskii-Moriya (DM)相互作用的鍵交替海森伯模型, 其中DM相互作用是Dzyaloshinsky[11]和Moriya[12]首次提出的用來描述弱鐵磁體的相互作用, 它也是導致磁阻挫的原因之一.近年來, 研究發現DM相互作用可以影響許多體系的磁性和臨界性質[13].在Ising和XXZ模型中, 考慮了DM相互作用后, 系統將從反鐵磁的自旋Néel相轉變為自旋液體相[14].Thio和Aharony[15]觀察到含有DM相互作用的反鐵磁La2CuO4中反鐵磁相變的三臨界點.一般情況下DM相互作用很弱, 但是Zhao等[16]研究了DM相互作用對苯甲酸銅Cu(C6D5COO)23D2O低能磁激發的影響, 發現DM相互作用對實際材料的影響確實非常重要.另外, 許多反鐵磁材料都能通過DM相互作用來描述的, 例如Yb4As3[17],BaCu2Si2O7[18]和 CsCuCl3[19]等.由于 DM 相互作用引起材料不同尋常的物理性質, 激發了人們對含有DM相互作用系統研究的廣泛興趣.

本文基于張量網絡態表示的無限矩陣乘積態(iMPS)算法, 利用無限虛時間演化塊抽取方法, 數值上得到了此系統的基態波函數.基于矩陣乘積態的基態波函數計算了系統的量子糾纏熵及非局域拓撲序.研究發現, 在DM相互作用存在的情況下,隨著鍵交替強度由弱變強, 系統從拓撲有序的Haldane相轉變為局域有序的二聚化相, 從系統基態的von Neumann熵、局域二聚化序及非局域拓撲序參量得到了較為精確的相變點和并基于 von Neumann 熵和序參量確定了系統完整的相圖.此外, 為研究此類拓撲相變的標度行為, 本文對相變點附近的二聚化序的一階導數及非局域拓撲弦序做了數值標度擬合, 分別得到了不同DM相互作用強度下刻畫相變臨界性質的特征臨界指數 α 和 β , 并且分析了DM相互作用在此模型中對相變臨界性質的影響.

2 iMPS算法

對于本文研究的自旋1含有DM相互作用的鍵交替海森伯模型, Jordan-Wigner變換已不再適用.近年來基于張量網絡表示的數值方法讓我們能夠更深層次刻畫和理解自旋系統的臨界現象[20].在張量網絡算法中, 特別是針對無限的一維自旋系統, 波函數被表示成iMPS的形式[11], 即

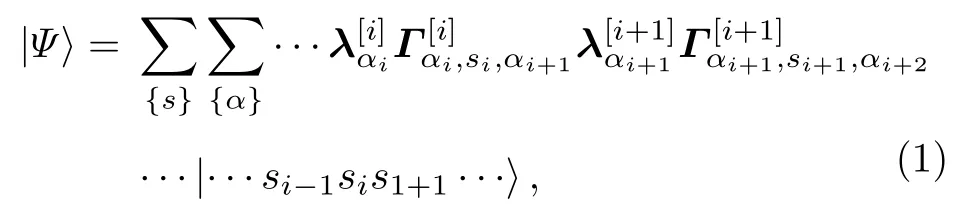
其中 | si〉 是希爾伯特空間中i格點的基矢, 對角矩陣中的元素是兩半無限鏈的施密特分解系數,是對應格點位置的一個三階張量, 其值可以取 1 ,2,···,χ , χ 是iMPS算法中的截斷維數.si值取為 1 ,2,···,d , d是單個格點希爾伯特空間維度.利用虛時間演化方法, 可以將系統的近似基態表達為

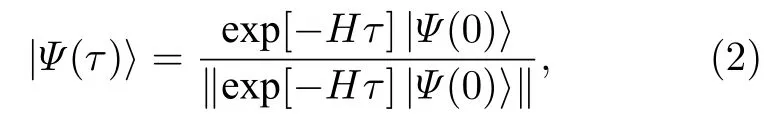
其中H表示系統的哈密頓量, Ψ (0) 為任意給定的系統初態.在算法的迭代更新過程中, 有效的方法是對虛時間演化算符進行Suzuki-Trotter分解[21],使之約化為一系列只作用于兩個近鄰點的兩點演化算符的乘積.一旦得到了無限系統的基態波函數, 就可以將之施加在相應的物理算子上, 從而計算出相應的物理量.

3 模 型

在微擾理論中, DM相互作用是一種由于在低對稱的磁系統中自旋軌道相互耦合而自然產生的反對稱各向異性相互作用.然而在實際分析的過程中, 對于具有DM相互作用的模型的研究極為困難, 卻也極大地豐富我們對低維磁性材料中量子現象的理解[22,23].

為了研究DM相互作用對含有非局域序參量的量子相變的影響, 本文選取了一維具有DM相互作用的自旋1鍵交替反鐵磁海森伯模型.其哈密頓量可以表示為

其中 Si為格點i處的自旋1算符.δ 是系統結構對稱性破缺的鍵交替幅度參數, D是DM相互作用強度, J是反鐵磁最近鄰自旋相互作用系數, 本文計算中取 J =1.標準的自旋1海森伯模型處于自旋固體態的Haldane相, 具有較小的能隙.由于Z2×Z2的隱性對稱破缺, Haldane相沒有局域序參量, 但存在非局域的長程序, 是一個拓撲有序相[24].當海森伯模型被施加鍵交替效應后, 結構上的對稱性被打破, 系統歷經一個Haldane相到二聚化的高斯相變[25], 其相變點位于 δ ≈0.260.本文將主要研究存在DM相互作用時, 鍵交替的海森伯模型的量子相變和臨界行為.

4 數值模擬

4.1 量子糾纏

近年來, 基于量子信息的量子糾纏已經被應用到研究量子相變中.量子糾纏是一種用來測量一個給定系統中量子關聯的有效方法.在量子信息學中, 人們已經提出并使用了各種不同的方式來度量系統的糾纏, 這其中包括von Neumann熵,concurrence, Negativity 和幾何糾纏等.大量的研究證明了量子糾纏是一個能夠有效探測系統量子相變點的普適方法[26?28].兩體 von Neumann 糾纏熵S被定義為 S = ?Tr[ρLlogρL]= ?Tr[ρRlogρR],式中 ρL和 ρR分別是半無限鏈子系統L和R的約化密度矩陣.在張量網絡表示中, von Neumann 熵定義為

其中 α 表示半無限鏈 L (?∞,···,i) 和 R (i,···,∞) ,λ是兩個半無限鏈間的Schmidt分解系數, 可以由轉移矩陣的奇異值分解得到.

在鍵交替效應存在的情況下(鍵交替參數 δ 的變化范圍為 δ ∈[0,1]), 系統結構上的對稱性被打破.因此, 圖1 給出了 D = 0.5 和 D = 1 時系統的奇鍵 (第 2 i+1 個格點) von Neumann 熵 So和偶鍵 (第 2i 個格點) von Neumann 熵 Se, 其中, 截斷維數選取為 χ =32.從圖1可以看出, 隨著鍵交替參數 δ 的變化, 奇鍵熵 So和偶鍵熵 Se在整個參數范圍內的值是不同的, 但在和時都出現了峰值.此峰值位置就對應著量子糾纏發散的位置, 也意味著系統在此位置發生了相變.實際上, 想要得到系統相變點的精確位置, 截斷維數 χ 需要達到無窮大.為了保證計算數據的精確度, 計算過程中比較了 D =0.5 時χ=32和 χ =50 兩種截斷維數下得到的相變點都為其位置沒有發生明顯移動, 說明截斷維數為 χ =32 已足夠保證數據精度.

在鍵交替海森伯模型中, 當鍵交替參數 δ 逐漸增大到 1, 奇鍵熵 So逐漸趨于飽和, 而偶鍵熵 Se逐漸降低為零, 系統在 δc≈ 0.260 從Haldane相轉變為二聚化相, 并最終呈現完全的奇鍵二聚化[25].但在含有DM相互作用的情況下, 偶鍵熵 Se并沒有降低為零.同時, 相變點也發生了后移, 從D=0時的后移到了 D =0.5 時的0.305, 當 DM 相互作用繼續加大到 D = 1 時, 相變點繼續后移到了.這說明DM相互作用抑制著系統的二聚化, 并最終會打破系統的完全二聚化.

4.2 序參量

圖1 D = 0.5 和 D = 1 時 (a)奇鍵 von Neumann 熵 So 和 (b)偶鍵 von Neumann 熵 Se 隨 δ 的變化Fig.1.(a) Odd-bond von Neumann entropy So and (b) even-bond von Neumann entropy Se as a function of δ for D = 0.5 and D = 1.

不同相中的序參量可以幫助人們更為深刻地理解量子系統所發生的量子相變.在鍵交替效應存在的情況下, 系統結構上的對稱性被打破, 表現出結構上的二聚化行為.對于含有局域序的二聚化相, 其序參量就是近鄰自旋關聯的長程交替, 也就是二聚化序, 其表達式為

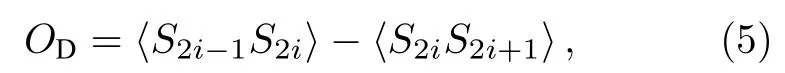
其中 〈···〉 表示期望值.

圖2(a)和圖2(b)分別計算了系統在DM相互作用參數選取為D = 0.5和D = 1時二聚化序OD隨鍵交替參數 δ 的變化.從圖2 可以看出, 在 δ=0時系統中的二聚化序 OD=0.一旦鍵交替效應存在, 二聚化程度就隨著 δ 的增大而增大, 二聚化序不僅存在于二聚化相中, 在拓撲有序的Haldane相中也存在.也就是說二聚化序存在于整個鍵交替幅度參數變化范圍.但是二聚化序在相變點附近變化較為劇烈, 其一階導數的最大值位置對應著von Neumann熵給出的相變點位置和.因此, 只要系統結構上的對稱性被打破, 局域的二聚化序就不能作為特有的二聚化相序參量來刻畫二聚化序, 但其一階導數可以用來標定相變點的位置.

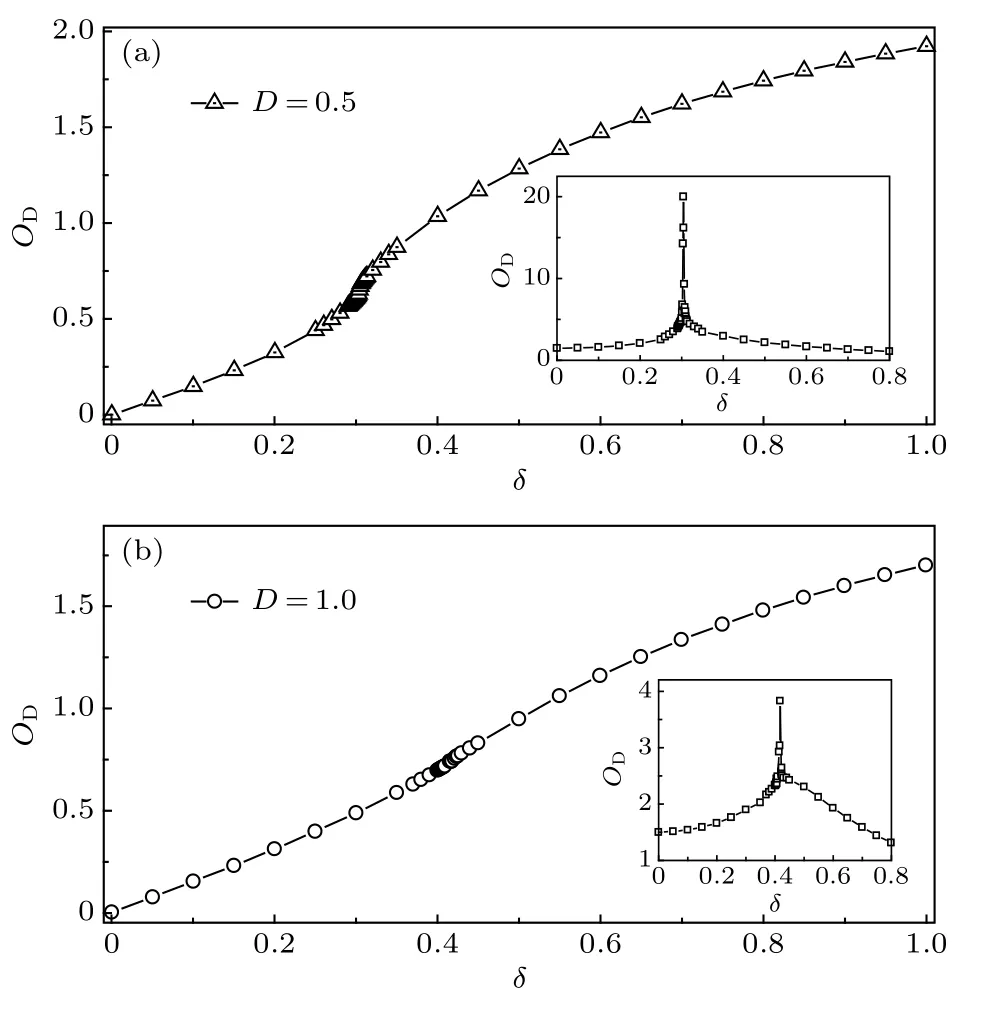
圖2 二聚化 序 OD 隨 δ 的 變化 (內 插圖為 OD 隨 δ 的一階導數) (a) D = 0.5, (b) D = 1Fig.2.Dimer order parameter OD as a function of δ for(a) D = 0.5 and (b) D = 1 (first derivation of OD in the insert).

同時, 為探究DM相互作用強度對系統結構二聚化的影響, 圖3計算了在 δ =1 時二聚化序OD隨DM相互作用強度D的變化.從圖3可以看出,隨著DM相互作用強度的增大, 二聚化序 OD逐漸減小.這意味著在此模型中由于DM相互作用的反對稱各向異性, 確實使得二聚化程度減弱, 抑制了系統的二聚化行為.因此, 這一結論也對von Neumann熵給出的結論提供了支撐.

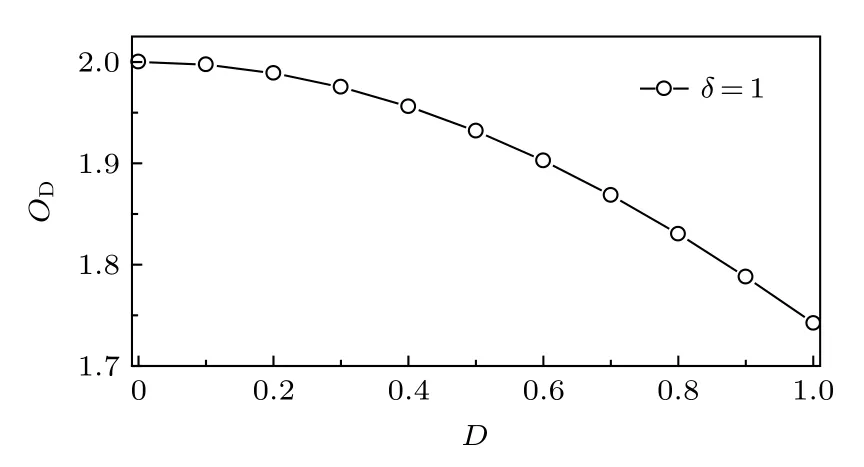
圖3 二聚化序 OD 隨 DM 相互作用強度 D 的變化, 其中鍵交替參數選取為δ=1Fig.3.Dimer order parameter OD as a function of DM interaction D for δ =1.

拓撲有序的Haldane相是一種無局域序參量的自旋固體相.隱性的 Z2×Z2對稱破缺可使得 Haldane相具有非局域拓撲弦序, den Nijs和Rommelse[29]首先引入了非局域拓撲弦序來表征自旋1 Heisenberg鏈中的拓撲有序Haldane相.弦序是遠距離格點長程弦關聯的飽和值, 在iMPS表示中可以直接計算出無限格點系統的非局域拓撲弦序值, 而不需要通過有限尺寸來進行外推[10].其表達式為

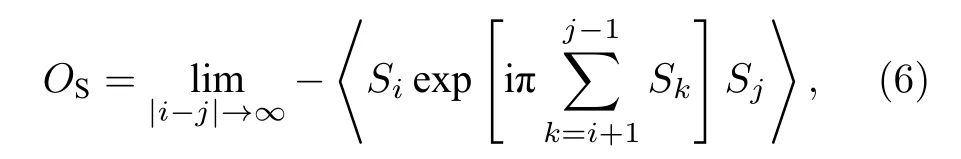
其中i和j是自旋格點的位置, 則格點間的距離就是 | i ?j|.

圖4計算出了非局域拓撲弦序 OS在DM相互作用參數選取為D = 0.5和D = 1時隨鍵交替參數 δ 的變化.由圖4 可知, 在 D = 0.5 時 δ?0.305和 D = 1 時 δ ?0.418 區域內, 非局域拓撲弦序OS都是有限值.而當在 D = 0.5 時 δ >0.305 和 D =1 時 δ >0.418 區 域 內 , 非 局 域 拓 撲 弦 序 OS的 值都為零.圖4結果表明, 當鍵交替參數 δ 增大到時, 系統從拓撲有序的Haldane相過渡到了局域有序的二聚化相.弦序給出的相變點的位置和von Neumann 熵以及二聚化序參量 OD一階導數給出的相變點是符合的.

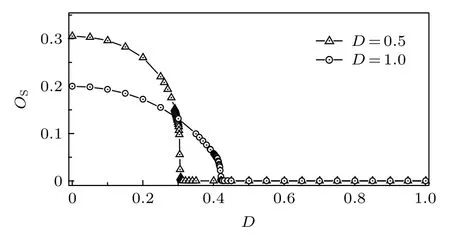
圖4 非局域拓撲弦序 OS 隨 δ 的變化Fig.4.Non-local topological string order parameter as a function of δ.

4.3 相 圖

為了反映系統結構對稱性破缺的鍵交替幅度參數 δ 和DM相互作用強度D共同作用下系統相變的性質, 基于iMPS算法的von Neumann熵和序參量確定的相變點, 圖5為一維含有DM相互作用的自旋1鍵交替反鐵磁海森伯模型的相圖.可以看出, 一條臨界線將二聚化相和Haldane相分開.當 D =0 時, 系統歷經一個 Haldane 相到二聚化相的高斯相變, 中心荷為 c =1 , 其相變點位于δc≈ 0.260[25].隨著DM相互作用強度D的增大,Haldane相的區域逐漸由窄變寬.這也印證了DM相互作用確實抑制了系統的二聚化.并且在相變過程中二聚化相和Haldane相始終是沿著同一條臨界線, 說明文中所選取的參數 D = 0, D = 0.5 和D = 1都處于同一條臨界線上.

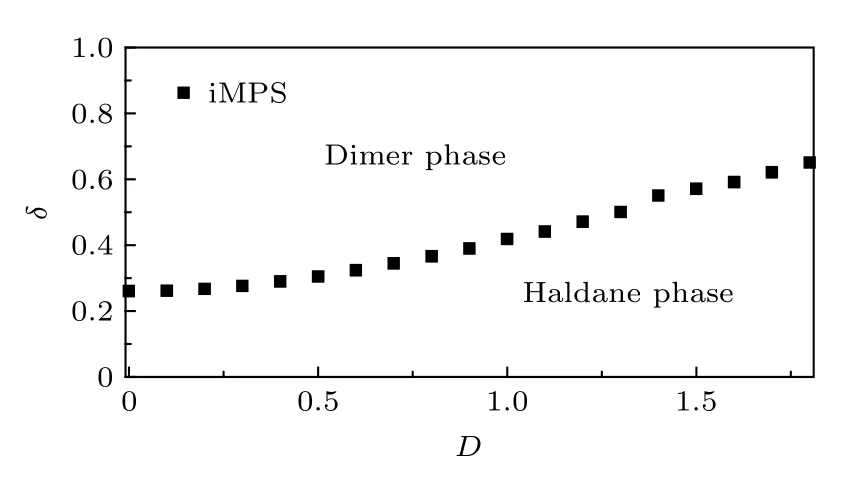
圖5 含有DM相互作用的自旋1鍵交替反鐵磁海森伯模型相圖Fig.5.Phase diagram of spin-1 bond-alternating Heisenberg model with DM interaction.

4.4 特征臨界指數

與量子相變相關的臨界指數規定了量子相變的普適類, 而這些臨界指數描述了一個量子多體系統在絕對零度時的關聯長度、磁化強度等物理量的發散特性.因此, 臨界指數是刻畫量子多體系統臨界行為的重要參數[30?32].然而系統基態所擁有的非局域拓撲序是無法用局域的序參量來刻畫的,此類相變的某些臨界指數是與非局域序緊密相連的, 也使得拓撲類相變超脫出Landau-Ginzburg-Wilson范式關于二級相變的范疇.對于拓撲類相變只有通過對非局域關聯及非局域序來刻畫其標度行為.

前面已經指出此模型中的二聚化序 OD并不能作為特有的二聚化相序參量來刻畫二聚化相.實際上這里的二聚化序 OD已經是一個能量物理量,其一階導數 ? OD/?δ 就類似于經典相變里的比熱CV.因此, 相變點附近局域二聚化序的一階導數?OD/?δ就可以擬合出與比熱相關的相變特征臨界指數.在圖6中, 基于張量網絡表示的iMPS方法計算出了對于DM相互作用參數為 D =0 , D=0.5和 D = 1 時在對應相變點0.305和附近局域二聚化序的一階導數 ? OD/?δ 隨著 | δ ? δc| 的變化.二聚化序的一階導數 ? OD/?δ 與 | δ ? δc| 是存在著特定的冪律關系,即 ? OD/?δ∝ |δ? δc|?α, 其中, α 是相變中與比熱CV相關的特征臨界指數.這里選取擬合函數為?OD/?δ=a|δ? δc|?α+ α0, 通過數值擬合可得到,D=0時 , αD=0=0.670 , aD=0=0.041 和4.868; D = 0.5 時, αD=0.5=0.338 , aD=0.5=0.342和以及 D = 1 時, aD = 1= 0.091,aD = 1= 3.819 和從而得到特征臨界指數 aD = 0= 0.670, αD=0.5=0.338 和 aD = 1=0.091.特別地, 對于 D = 0 時, 此相變的特征臨界指數為 aD = 0= 0.670, 其值近似等于 2/3.同時可以看出, 隨著DM相互作用強度增強臨界指數 α 逐漸減小.

圖7展示了對于 D =0.5 和 D = 1時在對應相變點附近非局域拓撲弦序 OS隨著 | δ ? δc| 的變化.從圖7可以看出,非局域拓撲弦序 OS與 | δ ? δc| 服從于 OS∝ |δ? δc|2β,其中 β 是相變中與磁性相關的特征臨界指數.選取擬合函數 l ogOS=2β log|δ? δc|+ β0, 通過數值擬 合 可 得 到 βD=0.5=0.101 和 βD=1=0.121 , 以 及從而得到特征臨界指數 βD=0.5=0.101 和 βD=1=0.121.

為了更為清楚地刻畫DM相互作用在此拓撲相變中對臨界性質的影響, 表1列出了不同DM相互作用強度下臨界指數 β 的擬合值, 可以看出特征臨界指數 β 隨著DM相互作用強度的增強在參數范圍內近似于線性增大.此模型在 D =0 時得到的特征臨界指數為 βD=0=0.082 , 其值近似等于1/12[25], 而在D = 1時得到的特征臨界指數為βD=1=0.121, 其值近似等于 1/8.在 D = 1 的情況下, 臨界指數 αD=1=0.091 和 βD=1=0.121 較為接近于二維Potts模型中 q =2 情形下的臨界指數值 α =0 和 β =1/8[30].由此可見, 量子相變中的不同量子自旋相互作用之間存在著彼此間的相互競爭.在這種相互作用競爭下, 由自旋軌道相互耦合產生的反對稱各向異性DM相互作用在此模型中影響著系統相變的臨界性質.這對于今后多量子自旋相互作用競爭下拓撲量子相變臨界性質的研究具有一定指導意義.

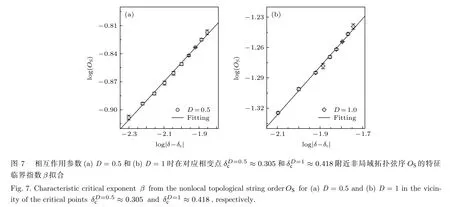
表1 不同DM相互作用強度下的臨界指數βTable 1.Characteristic critical exponent b for different DM interactions.

5 結 論

利用張量網絡表示的無限矩陣乘積態算法研究了一維具有DM相互作用的自旋1鍵交替反鐵磁海森伯模型的量子相變及拓撲序標度行為.基于矩陣乘積態的基態波函數計算了系統的量子糾纏熵.量子糾纏熵隨著鍵交替強度變化得到相變點位置可 以 看 出 DM相互作用抑制了系統的二聚化, 并最終打破系統的完全二聚化行為.本文進而計算了此系統中的局域二聚化序和非局域拓撲弦序, 確定了完整的系統相圖.結果表明, 系統從拓撲有序的Haldane相轉變為局域有序的二聚化相.同時, 只要系統結構上的對稱性被打破, 局域的二聚化序參量就不能作為特有的二聚化相序參量來刻畫二聚化序, 但其一階導數可以用來標定相變點的位置.此外, 通過對相變點附近二聚化序的一階導數和長程弦序的數值擬合, 分別得到了此相變的特征臨界指數 α 和 β 值,可以看出特征臨界指數 α 隨著DM相互作用強度的增強而逐漸減小, 同時特征臨界指數 β 隨著DM相互作用強度的增強而逐漸增大.對于此模型的研究揭示了不同量子自旋相互作用之間的彼此競爭, 對今后含有DM相互作用的拓撲量子相變中臨界行為研究提供了一定的借鑒與參考.