10%+10%為什么等于0.11

章勤瓊 郭盼

【摘 ? 要】用手機計算器計算10%+10%，可以得到不同的計算結果，這是因為百分數有不同的意義。百分數在理論上具有與分數相同的各種意義，但考慮實際應用應該突出其表示兩個量的比率關系的意義，這是百分數之所以產生的最大價值。在教學中，首先要加強對百分數意義的理解，特別是認識分數和百分數的異同。其次，將百分數的相關內容作為拓展資源，發(fā)展學生多方面的數學能力。

【關鍵詞】百分數;百分率;意義;計算器

百分數的教學是小學數學教學中的一個重要內容，百分數在生活中的應用十分廣泛。理解百分數的意義是學生學習百分數相關知識以及運用百分數解決有關實際問題的必備前提條件。[1]對于百分數參與運算的結果，存在不同意見。如10%+10%，大多數人認為可以轉化成小數0.1+0.1，結果為0.2;也有人認為，百分數表示的是兩個數的關系，不可以將其放在算式中進行運算，所以10%+10%沒法計算。除這兩種觀點之外，利用手機計算器計算“10%+10%”，會出現不同的計算結果0.11。那么，10%+10%不同的計算結果指向小學階段百分數的哪些意義？在教學中需要注意什么？我們應該對相關概念進行梳理，進而對教學有進一步的思考。

一、10%+10%為什么等于0.11

一般情況下，在進行有關百分數內容的計算時，需要先將百分數轉化為分數或小數，再按照分數與小數的計算規(guī)則計算結果。如10%+10%=0.1+0.1=0.2，這樣的計算并不存在什么難度，似乎也不應該有爭議。然而，在用手機上的計算器對10%+10%進行計算時，卻顯示10%+10%=0.11。這樣的結果顯然是令人驚訝的。對于這個結果，該如何解釋？

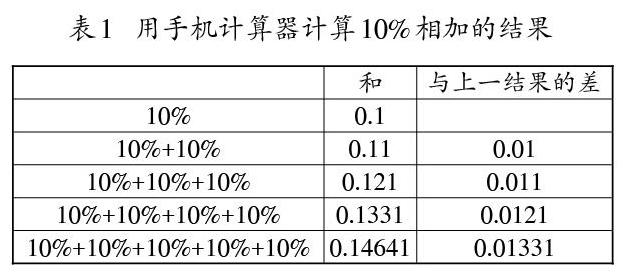
我們在計算時，按照小學數學四則運算的邏輯順序，將10%看成[10100]，也就是0.1，再做加減，結果為0.2。用計算器計算百分數的加法，之所以出現不同的結果，是因為百分號是個特殊的符號。百分數也叫百分率，這里的百分率是以哪個數為基數，也就是我們通常所說的單位“1”，即加上10%需要考慮的是加上哪個量的10%。計算出0.2的結果時，我們是將10%的單位“1”就當作數字1。然而，如果這里對10%的基數作不同的思考，就能得到10%+10%=0.11。如果繼續(xù)加上10%，可以得到這樣的結果：10%+10%+10%=0.121，10%+10%+10%+10%=0.1331;10%+10%+10%+10%+10%=0.14641……我們可以看出，后面所加的10%，都不是按照0.1的值來計算，每次加的10%的值分別是0.01，0.011，0.0121，0.01331，如果將增加的值與前面的和進行比較，可以得到如表1所示的結果。

通過對表1的觀察，容易發(fā)現，每個算式與上一算式結果的差正好等于上一算式和的10%，即所加上的10%是以原來的加數作為基準量，即將原來的加數看作單位“1”，再加上這個數的10%。如10%+10%=10% ×（1+10%）=0.11，10%+10%+10%=（10%+10%）×（1+10%）=0.11×1.1=0.121……如果計算減法，也會得到類似的結果，如10%-10%=0.09，這是10%×（1-10%）的結果。而10%-10%-10%=（10%-10%）×（1-10%）=0.081。事實上，加上或減去一個百分數，可以這樣計算：[a±b=a?（1±b%）]，這里的[a]是指[±b%]之前所有的數的和。事實上，想利用手機計算器計算兩個10%的數值的和，也是可以實現的。只需在10%外面分別加上括號就行，用手機計算器計算（10%）+（10%）的結果即為0.2，括號里面作為整體，自然不會以括號外面的結果作為基準進行百分率的計算。

因此，手機計算器的這種行為是對算法邏輯的不同選擇，而不是計算錯誤。那為什么在手機計算器中一般要采用10%+10%=0.11這樣的算法呢？最早的電子計算器并沒有百分號“%”，后來加入之后，在一定程度上解決了計算場景中常有的難點。人們在日常生活中經常遇到計算小費、利息、折扣等場景，這樣的計算邏輯會變得非常實用，而且更貼近人們的日常語言。例如，早餐8元，需要額外支付小費10%，利用計算器只需要輸入“8+10%”，即可得到8.8元，而不需要輸入“8+8×10%”或者“8×（1+10%）”，后面這兩種輸入，顯然要煩瑣得多，而且解釋起來也更加復雜。這樣的例子在生活中還有很多，如存入5000元，利息5%，到期所得只需輸入“5000+5%”，就可算出5250元。減法也是如此，如某件商品500元，打八折銷售，只需輸入“500-20%”，就能得到400元。而讓計算器計算500-20%=499.8這樣的算式，反倒沒有什么實際意義。

如果用計算器來計算乘法和除法，跟我們習慣的運算結果沒有差別，如10%×10%=0.01，10%÷10%=1。這是因為在乘除計算中，不需要涉及加上或減去哪個量的10%的問題，在生活中也不需要處理這樣的場景。因此，如果了解百分數作為“百分率”的意義，并聯系在生活中實際場景的實用價值，就能理解用手機計算器計算10%+10%為什么等于0.11。

二、小學階段百分數的意義

百分數的英語為percentage，詞根為“cent”，來自拉丁語centum（一百），percentage的意思為“每一百中的部分”。西方在15世紀就已經開始使用百分數的形式“per[co]”，在17世紀中葉的一本著作中，已經出現了用“per[oo]”的符號表示百分號，后來把前面的“per”也去掉了，而“%”這個符號的使用，則是現代的事了。[2]在數學辭海中，將“百分數”定義為一種特殊的分數，指分母是100的分數，或表示一個數是另一個數的百分之幾的數。[3]之所以說百分數是特殊的分數，是因為百分數是分母為100的繁分數。當N是一個數時，繁分數[N100]通常讀作百分之N，也寫作N%。[4]這里的N可以是整數，也可以是小數和分數。跟平常一般需要將分數化簡為分子分母為互質整數的最簡分數不同，在百分數中，需要保證分母為100，至于分子是什么形式，并不重要。