十六烷-水乳液界面電位極大值的理論計算

楊方源， 吳 豪， 朱源哲， 祖力胡馬·吾買爾， 余舒錦

(新疆農業大學 數理學院， 烏魯木齊 830052)

1引 言

界面上的分子電勢和其相應的分子結構是影響界面行為的重要因素，其中的電荷相互作用是一種重要的相互作用[1, 2]. 電荷相互作用被認為是分子與分子之間、分子與靜電場之間的相互作用，這種相互作用來自于外界或者不穩定的界面離子分布比如界面的雙電層結構[3]. 為了探測界面的分子行為，常用的探測手段有：化學滴定法[4, 5]，界面張力法[6, 7]，表面/界面電勢法[8-10]，布魯斯特角成像法[8, 11, 12]，電子順磁共振法[13]，中子反射法[14]，以及二階非線性光譜方法[7, 15-21]等.

眾所周知，界面上的分子所帶電荷很容易通過測量界面的電遷移率[22-26]、測量界面的電流或者電勢[9]從而得到其相應的Zeta電位值，從得到的Zeta電位值就可以轉化為界面的電荷信息. 理論上，Zeta電位值基于估衣-查普曼(Gouy-Chapman)理論的Graham方程表達如下[3, 27]：

(1)

界面電荷密度Γ或σ是Zeta電位ζ和體系總離子強度濃度I的函數，e是基元電荷，εr是溶劑的相對介電常數，ε0是真空介電常數，kT是熱力學能量，z是離子價態. 根據Graham方程可知，一般情況下，當界面有特定的離子時，Zeta電位隨著離子強度的增加呈下降趨勢. 然而，有研究報道證明電遷移率隨著離子強度有極大值的出現，根據Henry方程[28, 29]，由于離子表面的Zeta電位與電遷移率是呈正比的，因此電位也會伴隨有極大值的趨勢出現，對于電位極大值的出現已經有實驗和理論工作進行了報道[30-34]. 到目前為止，對于這一極大值出現的原因解釋有三個主流的觀點，一是界面上的特異性離子吸附[22, 26, 31, 33]；二是毛發層理論[24, 26, 32-34]；三是界面電導率的反常效應[35]. 然而在特殊的情況下，許多因素都應該考慮，例如，界面電導率的反常現象可以解釋界面雙電層上的斯特恩層上的離子吸附效應. 在Vanderput等人[31]的文獻報道中，毛發層的形成和導致的電導率的變化被用來理解表面覆蓋聚苯乙烯顆粒的流動電流和電勢. 共離子吸附模型[36]認為電遷移率出現極大值的原因是由于共離子與界面區域的離子有競爭作用，因此導致壓縮雙電層所致.

其中毛發層理論[37]也是被眾人所熟知的一種用來解釋電位極大值出現的理論，毛發層理論認為有一層流動的聚合物鏈在聚苯乙烯顆粒物的表面，由于顆粒表面與離子頭基之間的排斥作用，尾鏈伸入溶液的距離受到體系離子強度、pH值等因素影響. 低濃度時，尾鏈通過移動滑移面的距離來降低遷移率，這就導致降低了滑移面上電勢，也就是Zeta電位，隨著體系鹽濃度的增加，毛發層逐漸坍塌至表面從而縮短了滑移面與表面之間的距離，這就導致遷移率上升；在更高濃度的情況下，又回歸至經典模型，電解質濃度增加導致靜電屏蔽效應增強，從而電位下降.

Antonietti等人[38]也報道了不同的實驗結果，聚苯乙烯膠體粒子的電遷移率和Zeta電位隨著體系離子強度(KCl)的變化，借助O’Brien-White公式[39]理論聯系的電遷移率和電位之間關系，轉換為電遷移率與體系離子強度之間的關系. 他們的實驗結果表明，通過O’Brien-White方法從電遷移率反推計算出來的Zeta電位曲線并沒有極大值的出現，盡管其電遷移率的曲線有極大值. 這一結果表明了電遷移率的極大值現象實際上并不是反常的. 在隨后的實驗報道中，Folkersma等人[24]指出盡管利用O’Brien-White方法，計算出來的電位曲線隨著離子強度的變化仍有極大值出現，但是這一極大值現象并不明顯. 因此，關于電位會出現極大值現象，人們秉持懷疑的態度. 到目前為止，關于電荷，Zeta電位以及電遷移率隨著離子強度的變化問題都是膠體領域和界面研究領域的熱點話題.

在本文中，我們利用理論計算的方法研究了十六烷乳液界面電位和電遷移率之間的關系，利用O’Brien-White公式，通過測量得到的電遷移率值反推公式得到相應的Zeta電位值，計算結果表明 Zeta電位曲線規律隨著體系離子強度變化是由系統參數決定的. 進一步地，我們分析十六烷乳液表面油滴的電遷移率和電位隨著pH值和表面活性劑SDS濃度的變化規律，得出十六烷乳液界面電位是否出現極大值依賴于系統參數的選擇.

2實驗部分

2.1實驗材料

去離子水經超純水機(Water Purifier, WP-UP-UV-20，四川沃特爾水處理設備有限公司)制備，電阻率為18.25 MΩ·cm.

十六烷(99%, Sigma-Aldrich)用堿性氧化鋁(100-200目，阿拉丁)過濾六次，具體步驟參照文獻[21, 40]：將100 g堿性氧化鋁均勻裝入500 mL容量的具砂板存儲球層析柱中，約柱型體積的一半，先用75 mL十六烷潤洗柱子，然后將十六烷(1 L)倒入柱中，在過濾過程中十六烷流速約2 mL/min，收集過濾后的樣品，為純化一次的十六烷. 之后用純化一次的十六烷(75 mL)潤洗一根新的堿性氧化鋁柱層析柱，用同樣方法過濾得到純化兩次的十六烷. 以此類推，一共純化六次，最終1 L十六烷經六次純化后減少到約600 mL，之后用于實驗.

十二烷基硫酸鈉(SDS，99%, Sigma-Aldrich)用無水乙醇(99.7%，天津百世化工有限公司)和水的混合溶劑(V:V=95:5)重結晶三次，去除雜質, 這些雜質的存在，對其溶液的臨界膠束濃度(CMC),表面張力，表面粘度，以及其他物理性能都有著很大的影響[41]. 具體純化步驟為：5 g SDS加入50 mL醇/水混合液中，然后在磁力攪拌下使用冷卻回流裝置加熱至80℃，直至SDS完全溶解，室溫下冷卻結晶，抽濾干燥，如此過程重復三次，SDS分子結構式如圖1所示.

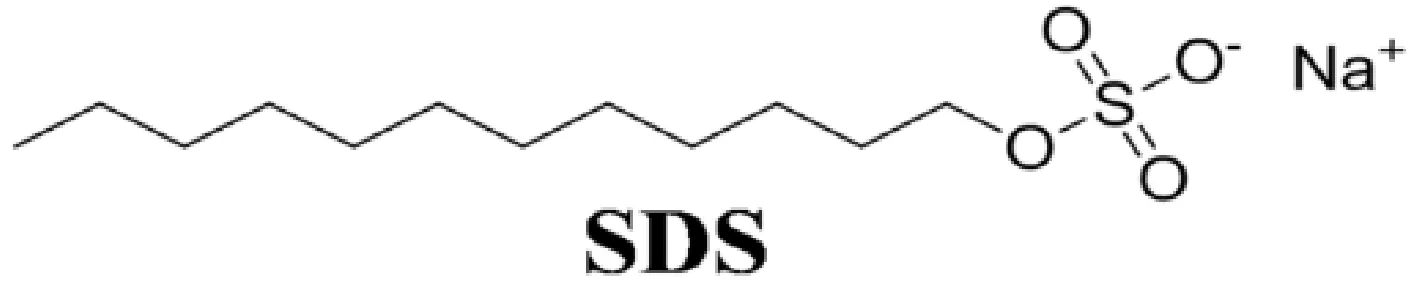
圖1 SDS分子結構式.Fig. 1 Molecular structure of the SDS surfactant.

氫氧化鈉 (NaOH, 99.99%, Sigma Aldrich)和鹽酸(AR reagent, 37% solution in water, Tianjin Baishi Chemical Co. Ltd, China)用于調節乳液的PH值.

氯化鈉 (NaCl, >99 %, Sigma Aldrich)高溫500 ℃灼燒至10個小時以去除雜質，溶于水然后通過0.025um口徑的濾膜(Merck Millipore Ltd.)過濾兩次以去除不溶性的雜質.

實驗中用到的玻璃器皿用食人魚洗液(H2O2: H2SO4體積比為 3:7)浸泡，用于去除殘余有機物，之后洗凈晾干待用. (注意：食人魚液具有強氧化性使時要慎重).

2.2乳液制備和穩定性測試

無表面活性劑的乳液的制備過程：將純的十六烷和DI水按體積比為1:50混合，首先通過均質儀(Omni, TM125-220, 8000 rpm)混合約1分鐘，接著在25±3℃恒溫水浴中磁力攪拌(500 rpm)15 min，然后在25± 3℃恒溫水浴中超聲(KQ-300DE, 300 W, 40 kHz,昆山超聲有限公司)10 min從而形成穩定的乳液. 待乳液靜置至常溫，將制備好的乳液溶液稀釋100倍用于測試. 利用動態光散射儀，將制備好的無表面活性劑乳液進行粒徑的測試，粒徑為200nm-300nm左右，并且粒徑能夠穩定在6個小時的時間內(其粒徑分布圖及制備好的乳液照片如圖2所示). 實驗中在制備好的乳液中加入酸、堿或陰離子表面活性劑，實驗中所需的 pH值均通過pH計(Mettler Toledo, PE20K, 電極：LE438)進行調節. 用HCl溶液將乳液調為pH=5后繼續加入HCl用pH計將乳液調為pH=2、3和4，加NaOH用pH計將乳液調為pH=6、7、8、9、10、11、12和13，之后分別測它們的電遷移率.

圖2 乳液粒徑分布圖(左)及乳液照片(右).Fig 2 The number distribution of the droplet size in the hexadecane-water emulsions prepared with the protocol described in the text (left) and the picture of the emulsion (right).

2.3電泳測量

電遷移率和乳液粒徑測試使用動態光散射儀器(DLS，ZS90，Malvern). 檢測樣品的示意圖如圖3所示. 測試過程激光波長為633 nm，測量角度為90°，測試溫度設定為25℃. 油滴的平均粒徑在特定的環境下保持相對穩定并且粒徑的偏差不超過10%. 同時，在本實驗中，乳液中加入了酸、堿以及陰離子表面活性劑，因此測得的油滴半徑范圍在80nm-300nm之間，但是在同一離子強度下，粒徑保持不變或者偏差不超過10%. 實驗中通過電位儀，我們首先紀錄的是電遷移率的值，因為電位儀采用的是電泳測試的方法，所以直觀的數據是電遷移率的值，然后通過O’Brein-White公式反推得到相應的Zeta電位的數值. 實驗數據采用三次測量后的平均值.

圖3 電位測量示意圖.Fig 3. The schematic diagram of Zeta potential measurement.

3結果與討論

3.1Zeta電位值與電遷移率值之間的關系

通常認為Zeta電位和電遷移率之間的關系由Henry 方程來描述. 基于Smoluchowski[42]公式和Hückel[43]公式，Henry[28]提出了電遷移率的方程，此方程適用于較低的ζ和任意的ka值，表達式為：

(2)

f(κa)=1-eκa{5E7(κa)-2E5(κa)}

(3)

其中En(κa)是n階積分項，f(κa)是Henry函數. 當κa→，f(κa)→1，公式(2)近于Smoluchowski公式，而當κa→0，于是f(κa)→2/3且公式(2)變為Hückel公式.

Henry公式認為球形粒子周圍的電勢分布是均一的，然而對于處在較高電勢下的粒子，其雙電層并不是對稱的，這種使得電勢分布不對稱的效應一般稱為弛豫效應. Henry方程并未考慮此弛豫效應，因此也就只適用于低階的Zeta電位. Henry方程在表達電位和電遷移率之間的關系時有其局限性，能夠完整表達電遷移率的式子隨后由Overbeek和Booth[44]提出，他們給出了電遷移率在任意電位值下的表達式. Loeb和Overbeek[45]利用計算機得出了電遷移率和電位公式的數值解. O’Brein和White在1978年發展了這種計算機模擬的方法，得到了公式的精確解. O’Brein和White推導電遷移率和電位之間的關系具體步驟如下：

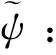
(4)

(5)

通過O’Brien公式(6)得到準確的電遷移率的值：

(6)

其中，

(7)

(8)

(9)

m±代表溶液中正負離子的遷移率. 這里，不同離子的遷移率可以從稀溶液中極限摩爾電導率求得.

為了得到電遷移率推導到電位的普適規律，我們對電遷移率和電位之間的關系進行了計算模擬，如圖4所示.

從圖中可以看出，從電遷移率推導至的電位曲線有兩條，除了個別電遷移率的點以外，其他一個電遷移率值均對應兩個Zeta電位值的點. 其中兩條電位圖中的點線圖表示電位值較大，其沒有物理意義并在以往的報道中并未進行闡釋. 基于此原因，我們只關注合理的那條曲線(即實線圖). 在圖4(a)中，可以看出電遷移率隨著體系離子強度的增加有個極大值的出現，然而根據公式反推至的電位曲線隨著離子強度的增加是單調下降的，這一趨勢符合Gouy-Chapman模型和以往人們報道的結果[43]. 在圖4(b)和(c)中，選用的粒子尺寸從150nm變為250nm，鹽的類型從NaCl變為KCl，這時不僅電遷移率隨著離子強度有極大值，由電遷移率推導至的電位值隨著離子強度的增加也有極大值的出現. 從圖4(d)中發現降低電遷移率的數值，得到的電位曲線仍有類似(b)和(c)的曲線變化趨勢.

從以上的計算結果可以看出，根據O’Brien-White公式從電遷移率反推得到的電位隨著離子強度變化的曲線，其曲線的變化趨勢依賴于所選體系，Zeta電位是否有極大值的出現依賴于體系參數的選擇.

3.2十六烷乳液Zeta電位在不同的pH值和SDS濃度下隨離子強度的變化

研究乳液表面的電位變化情況對于理解界面的分子行為有重要的作用，實驗中我們首先通過電位測量儀直接得出乳液電遷移率隨體系離子強度的變化情況，再通過O’Brien-White公式反推出相應的電位值，通過結合理論計算和實驗手段來進一步理解乳液表面的帶電信息. 這里，主要選取pH=7和pH=11, SDS濃度為50μM和SDS濃度為10mM的情況下，十六烷乳液Zeta電位隨著體系離子強度變化的數據點進行分析，這些濃度的選取涵蓋了較低的濃度范圍(pH=7 和50 μM SDS)和較高的濃度范圍(pH=11 和10 mM SDS). 依據O’Brien-White公式成立的極限條件ka≥10，我們這里選取NaCl的濃度大于等于100μM, 如此就能保證公式中的ka接近于10. 其中SDS濃度的選取，避開了其臨界膠束濃度的點，已有文獻證明，SDS的臨界膠束濃度會隨著體系離子強度的增加發生變化[46]，因此這里選取的濃度都遠離了其臨界膠束濃度. 實驗結果將通過電位測量儀直接測得的電遷移率的曲線與通過公式反推得到的真實的電位曲線進行比較. 通過上一部分的描述我們已經知道，實際上一個電遷移率的值對應著兩個電位值，在這里我們只保留了一組電位曲線，這是因為我們去除了結果中得到的那條沒有物理意義的曲線.

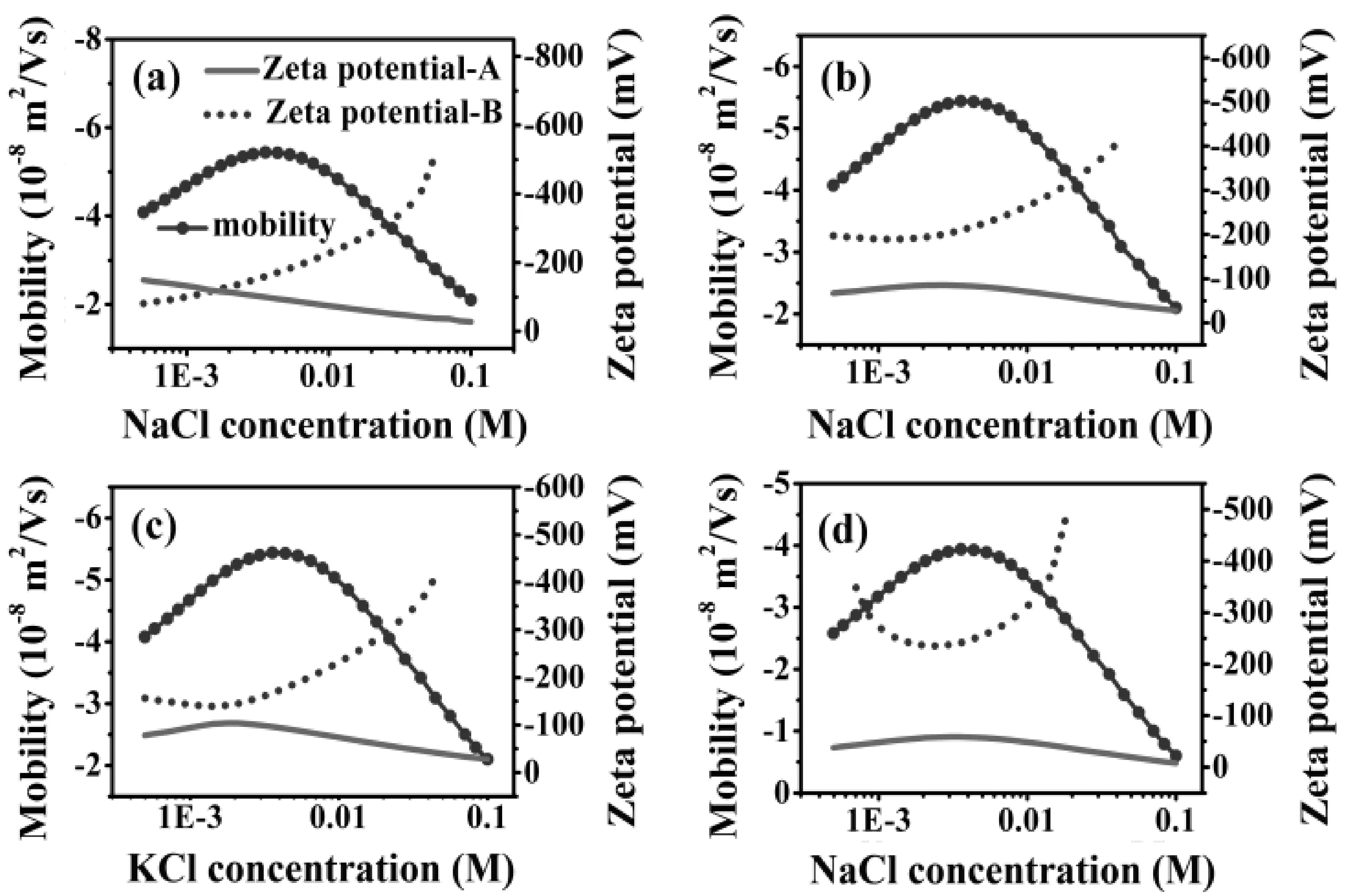
圖4 從電遷移率值計算得到電位值. 對于 (a) 和 (d), 粒子半徑a=150 nm,電解質類型是 NaCl. 對于(b), a=250 nm, 電解質類型是NaCl. 對于(c), a=150 nm, 電解質類型是KCl.Fig. 4 Calculated zeta potential curves (solid lines and dotted lines) from the ionic strength dependent electrophoretic mobility curves with a maximum (solid circles with lines). For(a) and (d), the radius of colloidal particles a=150 nm, the electrolyte type is NaCl. For (b), a=250 nm, the electrolyte type is NaCl. For (c), a=150 nm, the electrolyte type is KCl.

其中具體的電遷移率的值和由O’Brien公式進行反推得到的Zeta電位的值如下列各表所示，具體的推導公式也在上面的理論部分進行過推導，電遷移率與電位之間的關系如公式(6)所示，在這里不做重復推導，只給出電位和歸一電位之間的關系，如下所示：

(10)

通過計算結果發現，并不是所有的電遷移率的值都有對應的兩個電位值，有的點只有一個電位值與電遷移率的值對應，這可能與我們選取的體系有關.

通過測量得到的電遷移率的值以及公式反推得到其相應的電位值，實驗結果和計算結果如圖5所示，圖中(a), (b), (d)中的電位值和電遷移率的值都隨著體系鹽濃度的增加呈現單調下降的趨勢，而(c)圖中的電位值和電遷移率的值出現了極大值. 通過分析發現(b), (d)分別對應的是pH=11和SDS=10mM濃度這兩個點，這兩個濃度下吸附都分別達到了其飽和吸附. 而(a)圖中通過公式反推計算得到的電位值也并未出現極大值，分析原因是由于隨著體系鹽濃度的增加Na+濃度隨之增加，因為體系的pH=7, 乳液表面吸附OH-的量并未超過其吸附Na+的量. 因此這三個濃度下電位均為出現極大值現象. (c)圖中在SDS=50μM的濃度下，計算得到電位值出現了極大值的現象，乳液電位會隨著離子強度的增加出現極大值，這是因為隨著NaCl濃度的增加，Na+的增多會促進界面吸附更多的陰離子也就是DS-離子，那么使得乳液表面的電位逐漸增大，DS-離子的逐漸增加也會反過來導致表面活性劑分子(SDS)在乳液表面排列的更加有序，從而促進DS-在乳液表面的吸附，這時電位值達到最大，出現一個極大值的現象，然而當NaCl濃度過高時，電位反而下降，這是因為DS-與Na+之間很強的電荷作用，從而導致凈電荷下降，針對這一情況也有不同的結構模型來解釋[47]，表面活性劑在水油界面吸附電位出現極大值現象有助于我們理解水油界面上的分子結構和其排列行為.

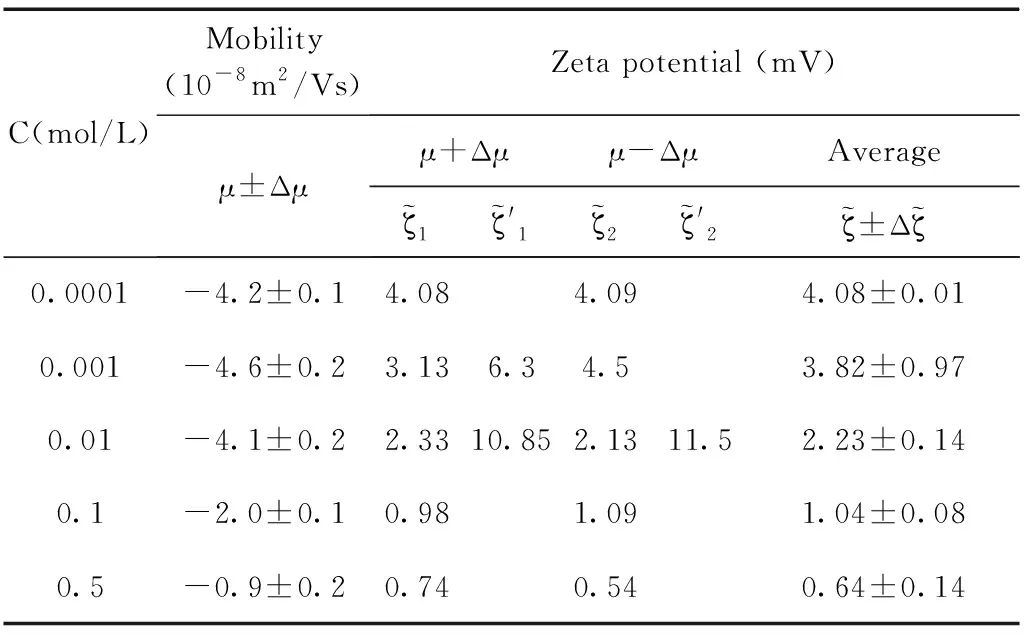
表1 乳液pH=7，電遷移率值與通過O’Brien公式計算得到的電位值.

圖5 乳液的電遷移率(圓點)和推導得到的Zeta電位值(方塊). (a) pH=7, (b) pH=11, (c) SDS=50uM, (d) SDS=10mM.Fig. 5 Converted ionic strength dependent zeta potential curves (empty squares) from the electrophoretic mobility curves (solid circles) measured in the hexadecane-water emulsions at pH 7 (a) and pH 11 (b), and the hexadecane-water emulsions in the presence of SDS at concentration of 50 μM (c) and 10 mM (d), respectively.

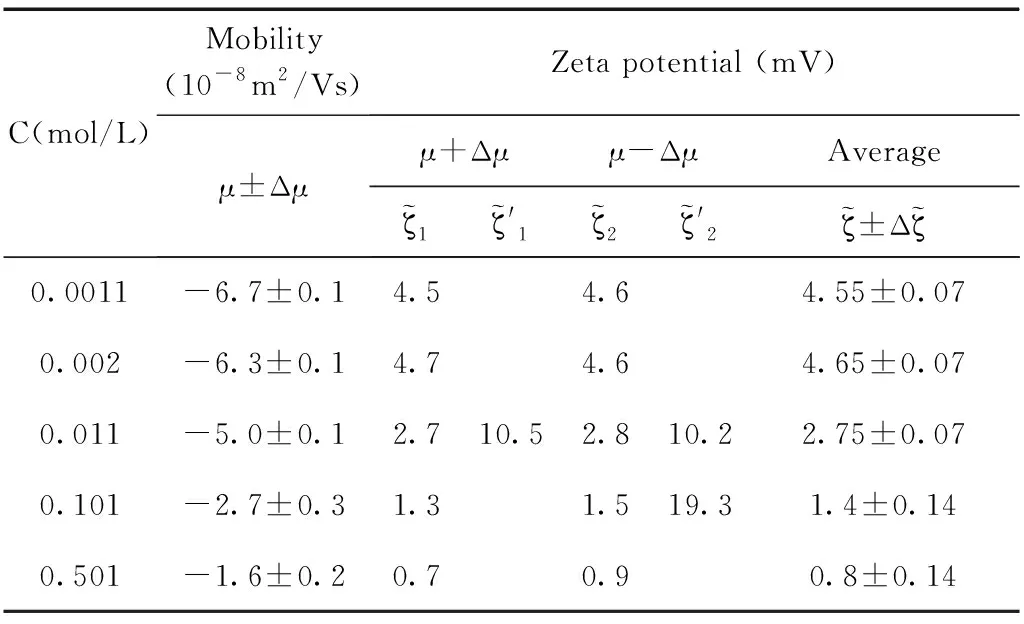
表2 乳液pH=11，電遷移率值與通過O’Brien公式計算得到的電位值.

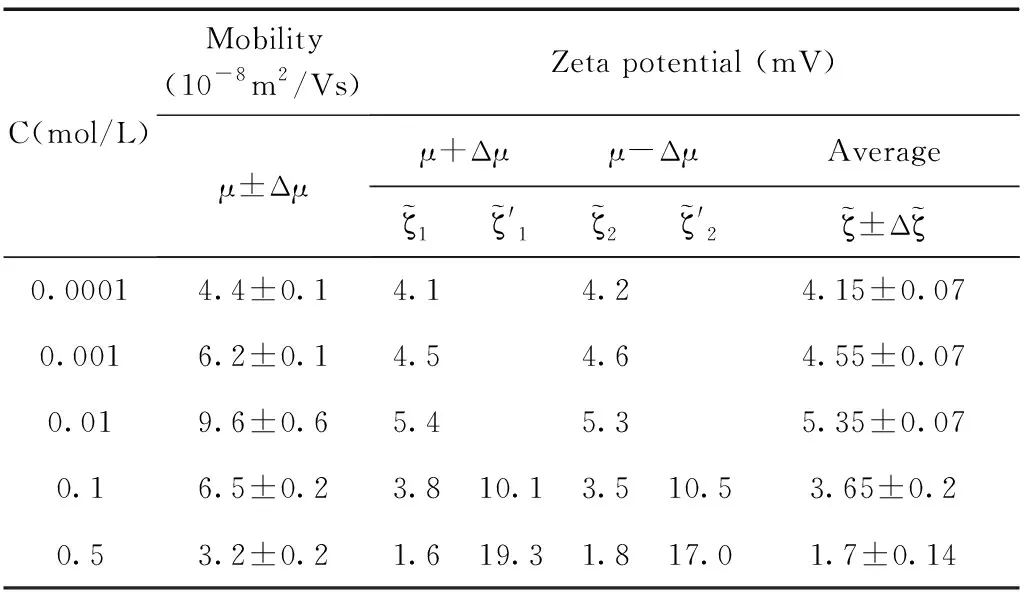
表3 乳液SDS=50uM，電遷移率值與通過O’Brien公式計算得到的電位值.

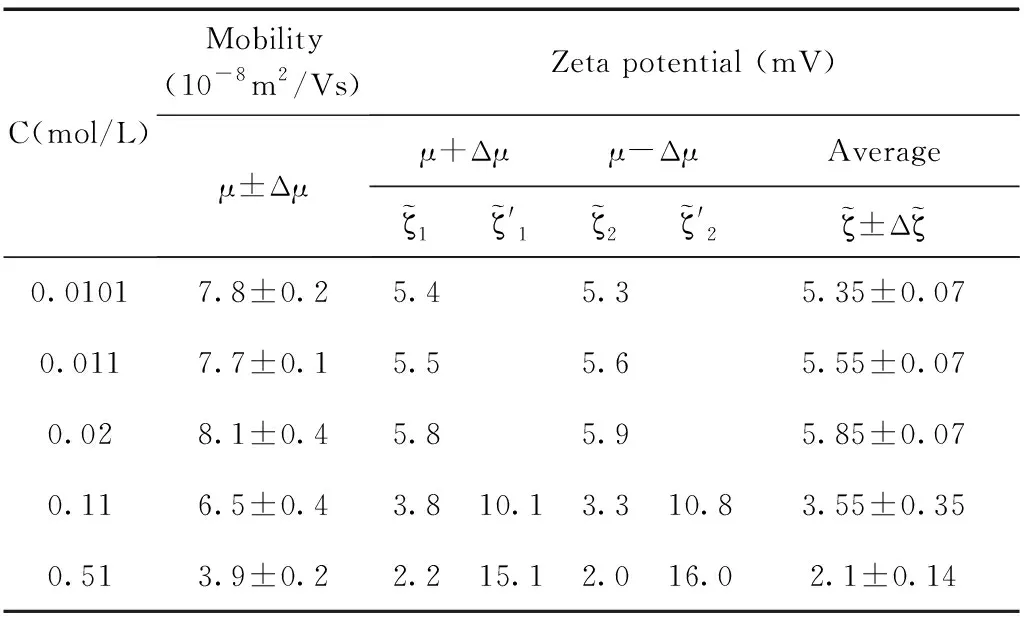
表4 乳液SDS=10mM，電遷移率值與通過O’Brien公式計算得到的電位值.

4小 結

本章借助O’Brien-White和估衣-查普曼理論，想到了從電遷移率值反推電位值這一轉換關系，通過O’Brien-White公式從理論上推導出乳液電位隨著體系離子強度的變化規律，從電遷移率的值與電位值之間的關系得出，一個電遷移率的值對應著兩個電位值，也就是說電遷移率和電位之間的關系不是一一對應的，在計算了大量的數據后，進行分析，得知其中有一條電位曲線是不符合物理意義的，所以經過篩選留下有物理意義的那條曲線. 其次，通過分析實驗測得的十六烷乳液電遷移率和電位隨著體系離子強度的曲線變化，可以得知電位是否出現極大值依賴于系統參數的選取，例如電遷移率數值的大小，體系電解質種類的選擇，以及離子半徑的大小等，這些參數的不同都會影響電位是否出現極大值這一現象.