醫用3D 打印批次智能排樣研究

李方娟，趙玉佳，趙君嫦，孟祥麗，郭強，孟繁欽

（1.牡丹江醫學院藥學院；2.牡丹江醫學院紅旗醫院，黑龍江 牡丹江 157011）

3D 打印是一種快速成型技術，采用數字技術材料打印機來實現的，運用粉末狀金屬或其它可黏合材料，通過逐層打印的方式來構造物體的技術。最近幾年，3D 打印技術在醫學各個領域得到了廣泛的應用，3D 打印肝臟模型、頭蓋骨、脊椎植入體等；3D 打印除具有個性化定制要求外，對于3D 打印醫用傳感器、助聽器外殼、康復醫療器械等具有批量打印要求。在批量3D打印加工中，當同時打印多個工件時，為提高工件的打印效率，通常將多個零件排布于打印機臺面內同時打印，即一個打印批次可以同時加工出多個零件，如一個批次無法完成全部零件的打印，就需要安排多個打印批次進行打印。因此，對打印工件進行合理的排樣，對縮短打印時間、提高3D 打印加工效率至關重要。3D 打印工件排樣問題是一個復雜的多約束優化問題，本文提出采用CHNN 神經網絡算法進行3D 打印排樣，并結合遺傳算法優化神經網絡，通過算法實現，完成了3D 打印批次排樣問題的研究。

1 排樣問題的求解

1.1 排樣問題數學模型建立

在批量3D 打印過程中，每個打印批次通常排布多個零件，又由于3D 打印是沿著零件的高度方向逐層進行打印的，因此，要想提高整個打印批次零件的加工效率，對打印零件進行合理的規劃排樣至關重要。由于3D 打印是逐層進行打印的，在同一批次工件打印中，打印時間是以高度最大的零件完成打印進行計算的。因此，要想提高整個批次打印零件的效率，必須保證同一打印批次內打印零件的高度差最小。設第Q 個打印批次內有n 個零件進行打印，各個零件的高度分別為h1，h2，…，hj，…，hn，其中打印零件件的最大高度為hmax，要使零件打印所需時間最短，應該滿足如下條件：

1.2 CHNN 用于排樣問題算法設計

連續型Hopfield(CHNN)神經網絡是1982 年由美國物理學家霍普菲爾德教授提出的一種單層反饋神經網絡。CHNN 神經網絡求解組合優化問題，就是在給定約束條件下，求出使目標函數極小（或極大）的變量組合問題。將排樣問題映射到CHNN 人工神經網絡：首先把排樣問題映射到一組神經網絡的特定組態上，此組態相應于排樣問題的可能解，然后構造一個適合于優化問題的能量函數E，此E 正比于優化問題的評價函數。所選的評價函數的好壞直接影響排樣的效率和結果。為了保證排樣結果的有效性，排樣問題的求解需要滿足如下條件：假定有P 個3D 打印零件，將其分成Q 組（即Q 個打印批次），則網絡使用PXQ 個神經元，將這些神經元按照P 行Q 列排列。當網絡達到穩定狀態時，上述神經網絡的求解問題必須滿足一定的約束條件。在滿足約束的條件下，優化排樣問題與約束之間的對應關系如表1 所示。

表1 排樣問題滿足的約束條件

3D 打印排樣問題的能量函數如下：

式中，D、E、F 為正系數； hmaxi為每組中排樣件的最大高度； hi為排樣件的高度；為第X 行第I 列的神經元輸出即排樣對象被分到標號為x 的組中。

其神經元之間的權值如下：

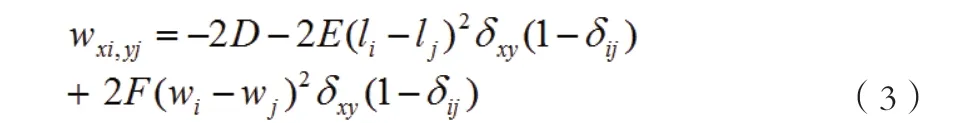
式中：

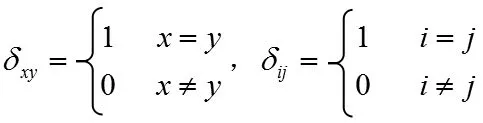
1.3 遺傳算法優化CHNN 神經網絡

遺傳算法是一種通過模擬自然進化過程搜索最優解的方法，通過復制、交叉、變異將問題解編碼表示的“染色體”群進行迭代進化，從而得到問題的近似最優解。將神經網絡中所有的神經元的連接權值編碼成二進制碼串或實數碼串表示的個體，隨機生成這些碼串的初始群體進行遺傳算法的計算。每完成一次迭代計算后，將碼串解碼為權值構成新的神經網絡，通過對所有訓練樣本進行計算得到神經網絡輸出的均方誤差從而確定每個個體適應度。經過若干代的計算，神經網絡將進化到誤差全局最小。

其求解過程如圖1。

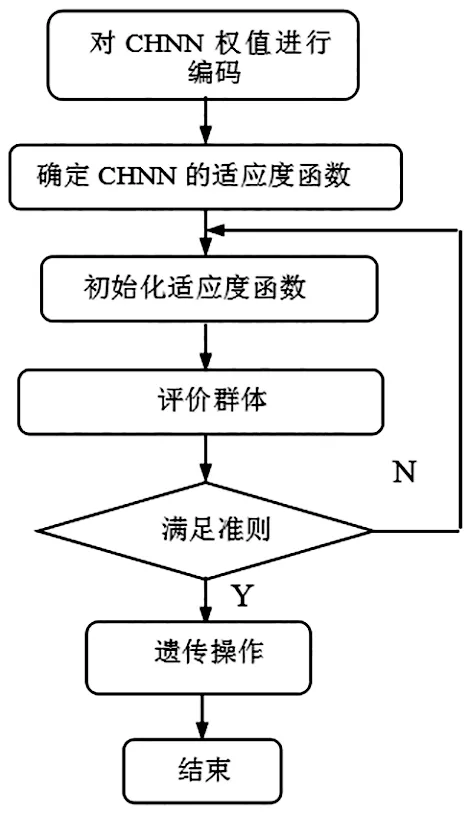
圖1 遺傳算法優化神經網絡流程

2 排樣問題實例驗證

將用遺傳算法優化的CHNN 神經網絡使用MATLAB 語言進行程序的實現。以20 個3D 打印零件的加工為例進行驗證，3D 打印零件的數量和相應尺寸如表2 所示。

排樣結果在輸出前建立如下規則：以被打印零件在水平面投影的最小包絡矩形作為輸出值，將打印工件在三維空間的排布問題轉化為二維圖形的輸出。打印圖形輸出結果如圖2 所示。

表2 排樣零件參數表

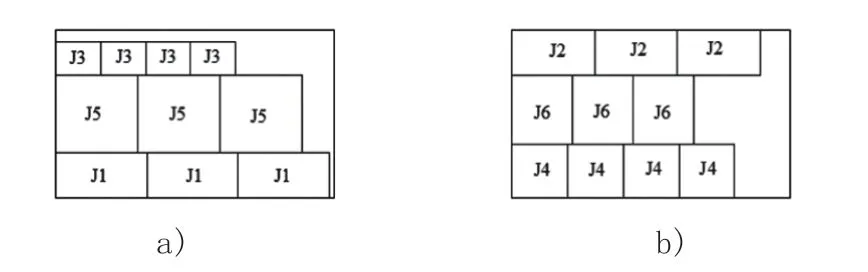
圖2 3D 打印圖形的二維輸出

3 結語

本文采用CHNN 神經網絡和遺傳算法結合解決3D 打印工件批次排樣問題，通過將排樣問題的目標函數映射到CHNN 神經網絡，建立了神經網絡的能量函數并完成了算法的程序實現，很好的解決了多約束的組合優化排樣問題，提高了3D 打印工件的加工效率。