基于差分進化算法優化BP神經網絡的鎳鎘電池壽命預測

盧順 李英順

摘要：鎳鎘電池組作為移動電源對于現代軍民用品是必不可少的，為了能夠有效的提高鎳鎘電池壽命的預測精準度，在建立BP神經網絡的電池壽命預測模型的基礎上，運用差分進化算法（DE）優化BP神經網絡連接的初始權值與閩值，預測結果表明：該改進的預測模型有較高的預測精度，誤差控制在5%以內，有效地提高了BP神經網絡的收斂速度，符合現實中鎳鎘電池實際運行的特性，對提高電池壽命評估的時效性和精確性具有重要的意義。

關鍵詞：鎳鎘電池;循環壽命預測;BP神經網絡;差分進化算法

中圖分類號：TM 912DOI：10.16375.j.cnki，cn45-1395/t，2020.02.013

0引言

鎳鎘電池在日常生活中作為移動電源，應用非常廣泛，但電池引起的安全事故不少，導致的經濟損失非常巨大，如果能夠通過采集到的歷史數據，提前預測電池的壽命狀態，就可以確定何時應該進行預防性維護以及何時應該更換電池，避免帶來損失，因此，對電池的壽命預測具有十分重要的現實意義和經濟價值。

目前在電池的壽命預測研究方面，可以分為兩類：基于數據驅動的方法和基于模型的方法，文獻[7]采用平均影響值（MIV）算法對BP神經網絡模型的輸入參數進行篩選，雖然提高了預測精度，但是收斂速度較慢，網絡的迭代次數較多，壽命預測效率減慢，文獻[8]運用的是基于行駛工況的磷酸鐵鋰電池壽命模型研究，缺點是實驗數據較少，誤差較大。

為了解決上述問題，對電池進行500次循環充放電測試，得到影響電池壽命的關鍵性能參數數據，電池的5個主要參數為：電池的容量、標稱電壓、內阻、放電終止電壓和充電終止電壓，通過對電池的健康狀態及失效機理進行分析，選擇內阻、放電終止電壓和充電終止電壓作為BP神經網絡模型的輸入，電池的放電容量作為輸出，并將差分進化算法運用到BP神經網絡預測模型中，利用差分進化算法具有較強的優化能力的優點，來改善BP神經網絡連接權值與閾值隨機產生的問題，并與其他相關的研究方法進行對比分析，預測精度明顯提高，迭代次數明顯加快。

1電池循環壽命預測模型的建立

1.1BP神經網絡壽命預測模型

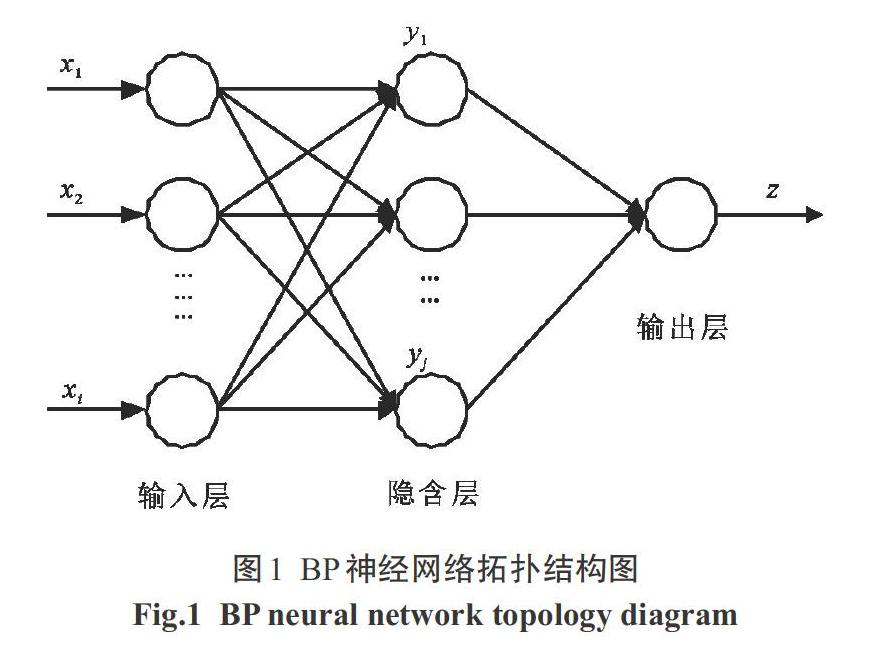
BP（BackPropagation）神經網絡算法是一種多層前饋神經網絡，其信號是正向傳播，而誤差是逆向傳播的，BP神經網絡過程可以拆分為兩部分：正向傳播和誤差的逆向傳播，其中正向傳播是從輸入層經過隱含層，再到達輸出層，逆向傳播是從輸出層到隱含層，然后到輸入層，在模擬過程中收集系統所產生的誤差，來不斷地調整隱含層到輸出層、輸入層到隱含層的權重和閾值，使網絡誤差達到設置的訓練精度要求，訓練結束，通過對鎳鎘電池容量衰退分析，選取鎳鎘電池充電截止電壓x1、放電截止電壓x2電池內阻x3作為輸入變量，輸出變量為電池循環放電容量z其網絡拓撲結構如圖1所示。

下面具體介紹輸入、輸出和隱含層相關參數計算公式，隱含節點yk的計算方法是用輸入層的網絡節點去乘相應的隱含層權值，再加上相應的閾值來得到的，同理可以計算出Zj計算公式為：

1.2差分進化算法

差分進化算法（Differential Evolution），簡稱DE算法，該算法是在遺傳算法等進化思想的基礎上建立的，模擬遺傳算法中的復制、交叉、變異來設計算法，本質是一種多目標（連續變量）優化算法，在多維空間中求整體最優解運用較多，該算法的原理是：首先，搜索是從一個隨機初始化的種群開始，然后，經過變異操作、交叉操作、選擇操作產生下一代種群;該過程重復進行，直到滿足停止條件。

算法的全局探索和局部開發能力決定著DE算法的搜索性能，種群規模、縮放比例因子和交叉概率等這些參數的選取至關重要，它首先生成隨機初始化種群：xi=（xi，1.xi，2.…，xi，D），其中i=1.2.…，N，D為問題的維數，N為種群大小。

1.2.1變異操作（Mutation）

從當前種群中的個體xi（g）產生下一個目標個體vi（g），基本原理是在種群中隨機的去除兩個個體，將這兩個個體進行相減、縮放，然后再與待變異個體進行向量合成，公式為：

1.3DE-BP網絡算法預測模型

差分進化算法對復雜函數具有較強的優化能力，由于初始權值是不應完全相等的一組值，即便確定存在一組互不相等的使系統誤差更小的權值，如果所設權值的初始值彼此相等，它們將在學習過程中始終保持相等，故而，在程序中，一般會設計一個隨機發生器程序，產生一組-0.5-0.5的隨機數，作為網絡的初始權值，針對初始權值與閾值隨機性問題，采用差分進化算法對其進行優化，尋找出最優的初始權值和閾值，整個算法流程是：先得到DE算法的初始種群，該種群主要由BP神經網絡的各連接的初始權值和閾值組成，對該種群進行變異操作、交叉操作和選擇操作，采用適應度值作為當前種群個體的評價指標，在種群中尋找最優的個體。只有當BP神經網絡的輸出值小于設置目標誤差時，整個流程才結束，整個DE-BP神經網絡訓練流程如圖2所示。

具體的操作步驟如下：

Step 1初始化網絡各個參數的設置（BP神經網絡和DE算法相關參數），

Step 2初始化權值和閾值，

Step 3初始種群的適應度值，選取訓練數據樣本對該模型進行訓練，計算均方誤差的平均值，然后作為適應度值。

Step 4運用1.2的公式進行變異操作、交叉操作和選擇操作，得到新一代的個體。

Step 5對產生的新個體計算其適應度值，

Step 6判斷是否滿足終止條件：如果滿足終止條件就會執行Step 7.如果不滿足終止條件就會返回Step 4重新執行。

Step 7對建立的DE-BP神經網絡循環壽命預測模型進行訓練，

2DE，BP網絡算法訓練

2.1訓練參數選取

采用常用的3層神經網絡，即輸入層、隱含層和輸出層，電池的充電截止電壓x1、放電截止電壓x2.電池內阻x3作為輸入變量，輸出變量為電池循環放電容量z，隱含層神經元數量由式（10）計算得出：

通過公式分析計算設置BP神經網絡和DE算法的相關參數，BP神經網絡參數選取：輸入層節點數為3.隱含層節點數量為8.輸出層節點數為1.選擇tansig函數為隱含層的激活函數，purelin函數為輸出層的激活函數，trainlm函數作為訓練函數，誤差值MSE設置為0.00004.小于該值時算法性能達到收斂精度，訓練到此結束，差分進化算法參數與選取：種群大小Ⅳ設置為30.縮放因子F設置為0.5.交叉概率CR設置為0.3.最大進化代數tmax設置為50。

2.2DE-BP網絡訓練

本文研究的電池為國內某廠家生產的單體容量1200mAh的鎳鎘電池，充電截止電壓為1.4v，放電截止電壓為1.0v，標稱電壓為1.2v在（20±5）°c工作溫度下，以0.5c恒流進行充電，直到電池電壓達到1.4v，然后以恒定電壓（cv）模式繼續充電，直到充電電流降至20mA，以2A的恒定電流（cc）進行放電，直到電池電壓降至1.0v一直這樣充放電循環，當電池容量下降到其閾值時判定電池失效，此時的循環次數就是電池的剩余壽命，從實驗數據庫中選擇0-400組數據作為訓練數據，其中另選400--415組數據作為測試樣本數據，在MATLAB R2018a軟件環境下，建立DE-BP算法模型，把400組訓練數據導入該模型中進行訓練，在整個過程中，利用DE算法求解BP神經網絡結構中最優的初始權值和閾值，最后完成整個DE-BP神經網絡模型的訓練，得到鎳鎘電池循環壽命預測模型。

3DE-BP網絡訓練結果與分析

把相同的訓練樣本數據導入BP神經網絡算法模型和DE-BP神經網絡算法模型中進行訓練，得出BP訓練誤差曲線圖和DE-BP訓練誤差曲線圖，如圖3和圖4所示，通過對比圖3和圖4發現，同樣達到訓練精度條件下，DE-BP神經網絡算法的迭代次數比BP神經網絡算法的迭代次數要減少，這可以說明在訓練數據相同時，差分進化算法確實能夠起到優化BP神經網絡的效果。

采用BP神經網絡算法訓練的誤差曲線如圖3所示，經過250次迭代后，訓練誤差值（MSE）小于設定的0.00004.算法性能達到收斂精度。

采用DE-BP神經網絡算法訓練的誤差曲線如圖4所示，經過95次迭代后，訓練誤差值（MSE）小于設定的0.00004.與圖3進行對比，發現運用差分進化算法優化后的BP神經網絡算法，其迭代次數明顯減少，相應的收斂速度加快。

為了說明優化后的預測模型能夠提高預測精度，即DE-BP神經網絡預測模型，如表1和圖5所示，從實驗數據庫里選取實測值作為驗證數據，和兩個預測模型輸出值進行對比，表1表示循環容量預測值與實際值對比，圖5表示改進前后循環容量對比曲線。

由圖5可知，當電池的失效閾值設置為0.75Ah時，BP神經網絡預測電池在405次充放電循環時失效，而優化過后的DE-BP神經網絡預測在407次充放電循環時失效，而且DE-BP網絡預測輸出值比BP網絡預測輸出值更接近真實值，預測精度有較大的提高，由表1可知，通過DE算法對BP神經網絡的初始權值和閾值進行優化以后，DE-BP網絡預測的最大相對誤差為3.0%，控制在5.0%以內;而BP神經網絡的相對誤差9.8%，控制在10%以內，相較BP神經網絡有很大改進，預測模型的精確度得到了提高，收斂速度也加快了，有效驗證DE算法能夠優化BP神經網絡預測模型，

4總結

通過對鎳鎘電池的容量性能衰退進行分析，建立了一種基于差分進化算法和BP神經網絡融合的模型;運用DE算法對BP神經網絡連接的初始權值和閾值進行尋優，減少了初始權值和閾值具有的隨機性問題和神經網絡迭代次數，加快了數據的處理速度，提高了鎳鎘電池壽命預測的效率與精度，在現實生活中對電池進行預防性維護以及更換有重要意義，節約了大量成本。